To Find Resistance of a Given Wire Using Meter Bridge and Hence Determine the Resistivity (Specific Resistance) of its Material

Samuel Hunter Christie created the Wheatstone bridge in 1833, which was then refined and popularized by Sir Charles Wheatstone in 1843. A Wheatstone bridge is an electrical circuit that balances the two legs of a bridge circuit, one of which contains the unknown component, in order to measure an unknown electrical resistance. The circuit's capacity to deliver incredibly exact readings is its main advantage, in contrast with something like a simple voltage divider which gives some extra resistance to the circuit thus causing errors in measurement. It works similarly to a potentiometer since both help take measurements using a null point.

Table of Contents

1. Aim

2. Apparatus required

3. Theory 

4. Procedure

5. Observations 

6. Result

7. Precautions

8. Lab Manual Questions 

9. Viva Questions 

10. Practical Based Questions 

Aim

To find the resistance of a given wire using a meter bridge and hence determine the resistivity (specific resistance) of its material

Apparatus Required

• Meter Bridge

• Wire About 1m Long (of Material Whose Specific Resistance is to be Determined)

• Resistance Box

• Rheostat

• Galvanometer

• Jockey

• One-Way Key

• Cell or Battery Eliminator

• Thick Connecting Wires

• Sand Paper

• Screw Gauge

Theory

Wheatstone's bridge operates on the same logic as a meter bridge. The device is made up of four resistors P, Q, R and S that are linked together to form the terminals named by letters $ABCD$. A key $K_1$ connects the terminals $A$ and $C$ to two terminals of a cell and another key $K_2$ connects terminals $B$ and $D$ to a delicate galvanometer $G$. 

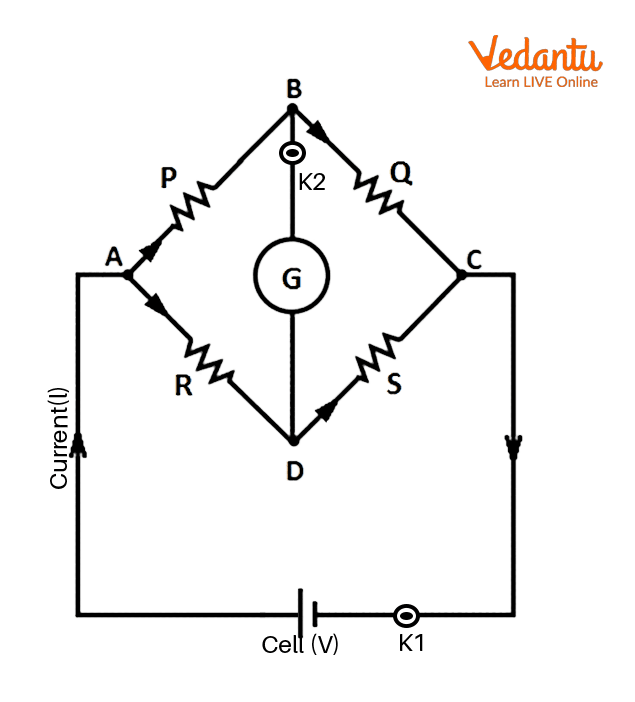
Wheatstone’s bridge

Wheatstone’s bridge is balanced for the condition $\frac{P}{Q} \ = \ \frac{R}{S}$. It is in this condition that the potential difference between points $B$ and $D$ are zero. Therefore, there is no deflection in the galvanometer and a null point is observed. By balancing a Wheatstone’s bridge, one can easily find the one unknown resistance if the other three are known.

A known resistance and the unidentified resistance S are linked in the gaps between A & D and C & D of the meter bridge, respectively. A terminal of the galvanometer G is linked to terminal B. A jockey $J$ that slides along the wire AC is attached to the other terminal of the galvanometer. In order to maintain a consistent potential drop along AC, a source of dc current is linked between A and C through a key $K_1$.

When the null point is obtained, $\frac{P}{Q} \ = \ \frac{R}{S}$ is satisfied. 

Also, for a wire, $Resistance \ (R) \ = \ Resistivity \ (\rho) \times \frac{Length \ (L)}{Cross-sectional \ Area \ (A)}$. 

Therefore, $R \propto L$. This proves that the resistance of wire $AC$ on which the jockey slides can be related to the length of the wire. 

Therefore, $\frac{P}{Q} \ = \ \frac{R}{S} \ = \frac {Resistance \ of \ wire \ of \ length \ DC}{ Resistance \ of \ wire \ of \ length \ DC }$ if $D$ is the null point. 

Since $AC \ = \ 100 \ cm$ the above equation can be related as $S \ = \ R \times \frac{l}{100 \ - \ l}$ where, $l$ is length of wire $AD$

Also, from (1) Specific resistance $\rho$ can be related after finding out the resistance, as $\rho \ = \ R \times \frac{A}{L}$ where $A \ = \ \pi \times (radius)^2$

Procedure

1. Using a screw gauge, determine the wire's average diameter. Divide the obtained diameter into two, in order to get the radius $r$.

2. Use a piece of sandpaper to remove the insulation from the ends of connected wires. Press each plug to tighten it to the resistance box $(R_{BOX})$.

3. Connect the circuit as shown in the figure. The wire of unknown resistance but known length should be connected in the gap between A and B.

Circuit diagram

4. Plug out some resistance from the resistance box. Bring jockey $J$ into touch with terminals $A$, followed by terminal $C$. The galvanometer needle should deflect in the opposite direction on touching each terminal. The null point will be located someplace on the wire $AC$ if the galvanometer exhibits deflection on both sides of its zero mark for these two sites of contact of the jockey. If not, change resistance $R$ so that the null point is at the centre of wire $AC$.

5. Check the circuit again, especially junctions, for continuity if there is a one-sided deflection.

6. Change the resistance $R$ and repeat step 4 for four different observations.

7. Change the resistances $S$ and $R's$ positions, then repeat steps 4 through 6 with the same five $R$ values. Make sure that the same length of resistance-wire $S$ is now in the gap between B and C while switching $S$ and $R$. The interchange takes care of unaccounted resistance offered by the terminals of the meter bridge.

Observation

Length of the wire of unknown resistance -

Measurement of diameter of the wire of unknown resistance -

Least count of the screw gauge (L.C.) - 

Zero error of the screw gauge - 

Zero correction of the screw gauge -

Observation Table for the Diameter of Wire

Observation Table for Unknown Resistance

Length of wire, $L = $

Radius of cross section of wire, $r = $

Resistivity of material of wire, $\rho =$

Substitute the values in $\rho \ = \ S \times \frac{\pi r^2}{L}$

Where, $L$ is length, $r$ is radius of cross section of wire and $S$ is resistance of wire

Error:

Error in specific resistivity- $\frac{\Delta \rho}{\rho} \ = \ \frac{\Delta S}{S} + 2\frac{\Delta r}{r} + \frac{\Delta L}{L}$

$\Delta r$ and $\Delta L$ are errors in the least counts of the measuring instruments and $\Delta S$ is the maximum error of the values obtained by following equations:

Error in resistance- 

$\Delta S_1 \ = \ \left [ \frac{\Delta l}{l} + \frac{\Delta l}{(100 \ - \ l)}\right ] \times S_1$

Similarly, $\Delta S_2 \ = \ \left [ \frac{\Delta l}{l} + \frac{\Delta l}{(100 \ - \ l)}\right ] \times S_2$

Assuming error in resistance from $R_{BOX}$ to be zero, greatest error is:

$\Delta S \ = \ \Delta S_1 \ + \ \Delta S_2$

Result

1. The provided wire's unknown resistance is determined to be $S \ + \ \Delta S \ =$

2. The wire is made of material which has a resistivity of $\rho \ + \ \Delta \rho \ =$

Here, $S$ and $\rho$ are mean values whereas, $\Delta S$ and $\Delta \rho$ are maximum errors.

Precautions

1. All of the plugs and connections need to be secure.

2. The jockey should gently be slid over the wire of the meter bridge to avoid altering the cross-section area.

3. Only when taking observations should the plug-in key $(K_1)$ be inserted.

4. The cable should have a null point in the middle of the wire $AC$ (around $30 \ cm$ to $70 \ cm$).

Lab Manual Questions

1. How will the observations change if the cross-sectional area of the meter bridge wire is not uniform?

2. What differences in the outcome would there be if the same experiment was carried out with $AC \ = \ 50 \ cm$ wire as opposed to $1 \ m$?

3. It is possible to locate the null point, or length l, to within $\pm 0.1 \ cm$ (say). How much uncertainty would the result have as a consequence of this error in calculation?

4. Making use of your observations, plot a graph between $\frac{(100 – l )}{l}$ versus $R$. Find the slope of the graph. What does it represent?

Viva Questions

1. $R$ and $S$ combinations are often desired to be selected so that the balancing point is close to the center of the meter bridge wire. Why? Is it advisable to have the same order of resistance for $R$ and $S$ to detect the equilibrium point?

2. Why is the meter bridge named so?

3. Why is the meter bridge preferred over the ohm’s law circuit to calculate an unknown resistance?

4. What is the null point? What is its significance?

5. When readings are not being taken, it is advisable that the key be disconnected to prevent unwanted wire heating. Why? What effects will heating have on the null point? Will its impact be significant?

6. It is preferred not to measure very high or very low resistances with a meter bridge. Why?

7. Why are the copper wires used to press the ends of the wire thick?

8. What are the possible sources of error in the experiment?

9. How will the observations change if the material used to make the meter bridge wire is not consistent in density?

10. The scale attached to the wire may not give the precise length. How can this error be minimised?

Practical-Based Questions

1. When a metal conductor connected to the left gap of a meter bridge is heated, the null point

1. Shifts towards right

2. Shifts towards left

3. Remains unchanged

4. Remains at zero

Answer: (a)

2. The null point is obtained in a meter bridge at a distance of $25 \ cm$ from $A$. If the resistance of value $14 \ \Omega$ is shunted to $S$, a null point is observed at $45 \ cm$. Value of $S$ is

1. $15.364 \ \Omega$

2. $20.364 \ \Omega$

3. $25.364 \ \Omega$

4. $22.364 \ \Omega$

Answer: (b)

3. We can remove the end error in the meter bridge experiment by

1. Changing the wire used in meter bridge

2. Repeating the experiment by changing known and unknown resistance

3. Taking average value of resistances determined during b.

4. Both b and c

Answer: (d)

4. The meter bridge is used to

1. Measure the electric current in circuit

2. Measure the potential difference across a resistance

3. Measure the resistance of a resistor

4. Measure the power supplied in a circuit

Answer: (c)

5. If the radius of the wire of the meter bridge is doubled, what will happen to the balancing length?

1. The balance length will become zero

2. The balancing length will get doubled

3. The balancing length will remain the same

4. The balancing length will be halved

Answer: (c)

6. On what principle does the meter bridge work?

1. Potentiometer

2. Wheatstone’s bridge

3. Kirchhoff’s law

4. Ohm’s law

Answer: (b)

7. Meter bridge can be used to find the resistance of

1. High value

2. Moderate value

3. Low value

4. All of the above

Answer: (b)

8. The balance length in a meter bridge experiment is obtained

1. Extreme left end of wire

2. Extreme right of wire

3. At any point on wire

4. Somewhere in the middle of the wire

Answer: (d)

9. In a meter bridge the null point is found at a distance of $33.7 \ cm$ from terminal $A$ (known resistance $R$ is connected to the gap near to $A$). If the resistance of $12 \ \Omega$ is connected parallel to unknown resistance $X$ (which is connected to the gap near terminal $B$), the null point is found at $51.9 \ cm$. The value of $X$ is

1. $13.5 \ \Omega$

2. $27 \ \Omega$

3. $25.5 \ \Omega$

4. $3 \ \Omega$

Answer: (a)

10. For which of the following pairs of resistors, the balancing length is not $0.25 \ m$ in a meter bridge?

1. $1 \ \Omega, \ 3 \ \Omega$

2. $\frac{7}{3} \ \Omega, \ 7 \ \Omega$

3. $25 \ \Omega, \ 75 \ \Omega$

4. $2 \ \Omega, \ 3 \ \Omega$

Answer: (d)

Summary

A meter bridge works on the Wheatstone bridge principle and can be used to find out unknown resistances. When this bridge is balanced, the ratio of the resistances is equal, and no current passes through the galvanometer. It works similarly to a potentiometer since both help take measurements using a null point. By balancing a Wheatstone’s bridge, one can easily find the one unknown resistance if the other three are known.