To Compare the EMF of Two Given Primary Cells Using Potentiometer

A uniform wire AB with a low-temperature coefficient of resistance is stretched over a uniform wooden scale to make a potentiometer. The potentiometer's wire is organised into two or three rows, summing to about $400 \ cm$. Typically, a wooden board with a $100 \ cm$ scale fastened next to it has a wire fixed.

A voltmeter can only measure the difference in voltage between a cell's two terminals, whereas a potentiometer can measure the internal resistance and EMF of a particular cell.

Table of Contents

1. Aim

2. Apparatus R.equired

3. Theory 

4. Procedure

5. Observations 

6. Result

Aim

To set up a potentiometer and use it to compare the EMF of two given primary cells using potentiometer.

Apparatus Required

1. Potentiometer

2. Leclanche cell

3. Daniel cell

4. Two way key

5. Resistance box plug type $(0 \ to \ 1000 \ \Omega)$ 

6. Galvanometer

7. Voltmeter

8. Battery eliminator

9. Low resistance rheostat

10. Two one-way keys

11. Connecting wires

12. Sandpaper

Theory

The device works on the principle that when two points are at the same potential, no current flows through the wire connecting those points. To use the device, a potential is set across the wire of the potentiometer. Each unit length of the potentiometer has a certain potential, known as the potential gradient. It can mathematically be expressed as $\text{Potential gradient} = \dfrac{\text{Potential across potentiometer wire}}{\text{Total length of potentiometer wire}}$. 

When the jockey connected to one end of the cell of unknown EMF is slid over the potentiometer wire, it tries to balance the EMF of the cell with the potential of the wire. As soon as the length of the potentiometer to suffice the EMF of the cell is reached, the galvanometer shows no deflection. Thus the null point is said to be obtained. 

Mathematically, the EMF of cell $(E)$ and the length of potentiometer wire $(L)$ can be related as $E \ = \ k \times L$ .

Where $k$ is the potential gradient of the potentiometer wire.

Therefore, to compare the EMF of two different cells, the ratio of their EMF can be calculated as the ratio of the lengths of their null points as $\dfrac{E_1}{E_2} \ = \ \dfrac{L_1}{L_2}$ .

Procedure

1. Connect the circuit as shown in the potentiometer diagram. In the diagram, $E_1$ and $E_2$ are two cells of unknown EMF, and $E$ is the cell providing potential difference to the potentiometer circuit. The negative terminal of cell $E$ is connected to the end B of the potentiometer wire through a one-way key $K_1$ and a rheostat.

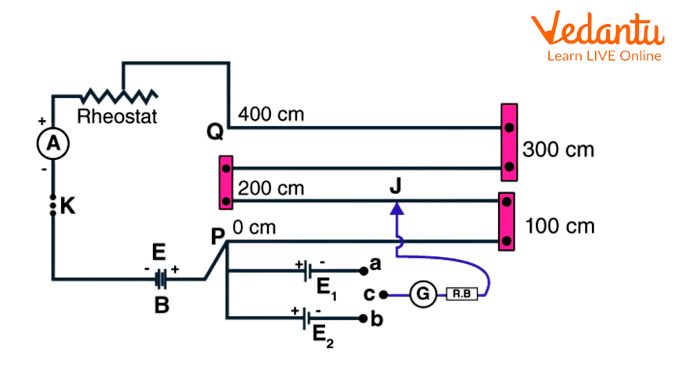
Circuit diagram

2. A two-way key is attached to the negative terminals of the unknown cells- $a$ and $b$ denote the two keys of the two-way key. This two-way key is capable of connecting one cell in the circuit at once. If both the switches are switched on in the key, the unknown cells are in parallel connection.

3. A resistance box $R_{BOX}$ is shunted through a key $K_2$. The common terminal of the two-way key $(c)$ is connected to one end of $R_{BOX}$.

4. The other end of the $R_{BOX}$ is connected to a galvanometer which is then joined to a jockey by its free end. The jockey can be slid on the potentiometer wire to obtain a null point in the galvanometer.

5. Plug is inserted in $a$ and $E_1$ is connected to the circuit and plug $c$ is inserted to complete the circuit. 

6. The key $K_2$ is left open, and rheostat resistance is minimal. High resistance (of the order of a thousand ohm) is removed from the resistance box. The jockey is touched at the zero ends of the potentiometer wire, and the direction of deflection in the galvanometer is considered.

7. Next, the jockey is brought in contact with the other end of the wire. The direction of deflection of the galvanometer needle must be opposite to that observed in the previous step; only then are the connections correct. Check connections if the deflections are in the same direction.

8. The jockey is gently slid over the potentiometer wire till the null point is obtained. 

9. The key $K_2$ is plugged in so that $R_{BOX}$ is short circuited and no resistance is offered. This makes a huge current flow, and the balance point can thus be found with more accuracy.

10. The length of the potentiometer wire is measured from point A to the point where the jockey is placed to find the null point. This length is noted as $L_1$.

11. Now, a plug is inserted in $b$ and $E_2$ is connected to the circuit. The null point is obtained in a similar manner as was done for $E_1$ , and the length is noted as $L_2$.

12. The rheostat is changed, and three different readings for $L_1$ and $L_2$ are obtained.

Observations

Calculate $\dfrac{L_1}{L_2}$ for each set of readings since $E \propto L$ where $E$ is EMF and $L$ is length.

To Calculate Error:

$\dfrac{\Delta\left (\dfrac{E_1}{E_2} \right )}{\dfrac{E_1}{E_2}}=\dfrac{\Delta L_1}{L_1} + \dfrac{\Delta L_2}{L_2}$

${\Delta\left (\dfrac{E_1}{E_2} \right )}=\left ( \dfrac{\Delta L_1}{L_1} + \dfrac{\Delta L_2}{L_2} \right )\times \left ( {\dfrac{E_1}{E_2}} \right )$

Result

The ratio of EMFs of the two unknown cells is:

$\dfrac{E_1}{E_2}\pm {\Delta\left (\dfrac{E_1}{E_2} \right )}_{max}$

$\dfrac{E_1}{E_2}$ is the main value of the ratio of EMFs of the two unknown cells.

Precautions

1. The resistance box must have good electrical contact for the keys plugged in.

2. To avoid creating any kinks in the potentiometer wire, the jockey should be slid with least pressure on it.

3. Prior to determining the balancing length with both cells, the position of the rheostat contact should not be altered for a single set of readings.

Lab Manual Questions

1. The potential difference is measured using a voltmeter connected in series with a battery's terminals. What distinguishes it from the EMF?

Ans: The EMF of the battery $(E)$ is the force that it exerts on the charge that passes through the wire to form current, whereas the potential difference $(V)$ is the amount of force that is received by a unit of electron moving from one location to another. The difference between these is the force involved in coming over the resistance of the battery $(r)$ and external wire $(R)$.

It can mathematically be expressed as $V \ = \ E \ - \ \dfrac{E}{R+r}r$

2. What conclusions would you draw if the galvanometer needle in your test setup kept swaying?

Ans: The probable cause of the same is the error in connection. The connections must be tightened to ensure no leakage of current.

3. To determine the ratio of the two cells' potential differences, use a voltmeter. Does it significantly differ from their emf ratio? What conclusions may you draw if not?

Ans: The ratio between the EMF’s of the cell measured using voltmeter and that using potentiometer is different. This is because the potential across the potentiometer is supplied by a cell of known EMF and not the one whose potential is to be determined whereas for a voltmeter, the potential is supplied by the cell of unknown EMF. Therefore, in the latter case there is some current taken up by the potentiometer resistance which leads to error in measurement.

4. Plot a graph of $L_1$ versus $L_2$ with $L_1$ on the y-axis and $L_2$ on the x-axis. Calculate $\dfrac{E_1}{E_2}$ from the slope of the graph.

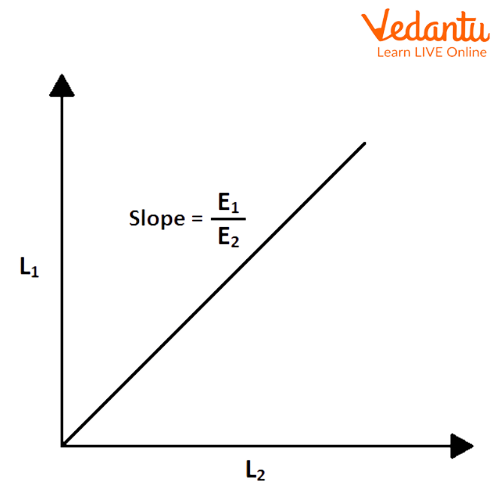
Graph between $L_1$ and $L_2$

Viva Questions

1. Explain what is the EMF of a cell?

Ans: Electromotive force or EMF of a cell is the energy generated by the cell which pushes the free electrons of a conductor, in order to produce electricity.

2. What is a potentiometer and state its uses?

Ans: A potentiometer is a device which usually has 4 wires of about $250 \ cm$ each, having a constant potential per unit length, and a metre scale attached to one end. It is used to find the EMF as well as internal resistance of an unknown cell. This is done using no deflection method, i.e., by obtaining a null point using a galvanometer.

3. On what principle does the potentiometer work?

Ans: Potentiometer works on the principle that when two points are at the same potential, no current flows through the wire connecting those points.

4. What is the preferred substance for making a potentiometer wire?

Ans: The wire used in potentiometers is typically constructed of an alloy, such as manganin or nichrome since these allow high resistivity and low-temperature coefficient of resistance.

5. What conclusion can be made if the deflection in the galvanometer is in the same direction?

Ans: If such a condition arises, it is due to the fact that the EMF of a cell is greater than that across the potentiometer.

6. What is a null point in the potentiometer experiment?

Ans: The null point is the point on the potentiometer wire for which no deflection is seen in the galvanometer.

7. State the possible sources of error in the experiment.

Ans: The possible sources of error are as follows:

• The area of cross section of the potentiometer wire may not be uniform throughout its length.

• Avoid continuous discharge of the two cells whose emf are to be compared by keeping the keys open when E1 and E2 are not in use.

• The length measurement may have error if the potentiometer wire is not taut and along the scale on the board.

• Multiple key jockey may not have correct alignment with the scale.

8. What is a rheostat?

Ans: A variable resistor that can be used to change the resistance in order to control the flow of electric current is called a rheostat.

9. Why does a galvanometer show no deflection at the null point?

Ans: At the null point, the potential difference between both the wires connected to the galvanometer becomes zero and thus no current flows through them. Therefore, the galvanometer does not show any deflection.

10. What are the voltmeter and ammeter used for?

Ans: The voltmeter is connected in parallel to the appliance, and is used to measure the potential difference across it. An ammeter is connected in series with an appliance and is used to measure the current passing through it.

Practical-Based Questions

1. In an experiment, a potentiometer is used to compare the EMF of cells $E_1$ and $E_2$. The null point for cell $E_1$ is found at $20 \ cm$, whereas that for cell $E_2$, is found at $30 \ cm$. Their EMFs will be in the ratio:

1. $\dfrac{2}{3}$

2. $\dfrac{1}{2}$

3. $\dfrac{2}{1}$

4. $\dfrac{1}{1}$

Answer: (a)

2.  The relation between EMF of unknown cell $(E)$ and length of null point $(L)$ is

1. $E \propto \dfrac{1}{L}$

2. $E \propto L$

3. $E = 10 \times L$

4. $E = \dfrac{1}{10 \times L}$

Answer: (b)

3. Potentiometer is an accurate and versatile device to make electrical measurements of EMF since the method involves

1. A combination of cells, galvanometer and resistances

2. Rheostat

3. Potential gradient

4. A condition of no current flow through the galvanometer

Answer: (d)

4. In a potentiometer circuit, a cell of EMF $1.5 \ Volts$ gives the null point at $36 \ cm$ length of wire. If another cell of EMF $2.5 \ Volts$ replaces the first cell, then at what length of the wire will the null point be obtained:

1. $65 \ cm$

2. $60 \ cm$

3. $21.6 \ cm$

4. $64 \ cm$

Answer: (b)

5. The potential gradient of the potentiometer wire depends on

1. Current passing through the potentiometer wire

2. The resistivity of material of the potentiometer wire

3. Area of the cross-section of the potentiometer wire

4. All of the above

Answer: (d)

6. The sensitivity of the potentiometer can be increased by:

1. Decreasing the thickness of the potentiometer wire

2. Increasing the length of the potentiometer wire

3. Increasing the temperature of the surrounding

4. All of the above

Answer: (b)

7.  Which instrument is used to measure deflection due to current?

1. Voltmeter

2. Rheostat

3. Galvanometer

4. Keys

Answer: (c)

8. Which value cannot be measured by a potentiometer? 

1. Capacity

2. Resistance

3. Electric current

4. Potential

Answer: (a)

9. If the radius of the potentiometer wire is doubled, the length of the null point will

1. Remain same

2. Increase

3. Decrease

4. Increase and then decrease

Answer: (c)

10.  If the length of the potentiometer wire is increased but same current is flowed through it, its sensitivity will:

1. Increase

2. Decrease

3. Remain constant

4. Cannot be predicted

Answer: (a)

Summary

Potentiometer works on the principle that when two points are at the same potential, no current flows through the wire connecting those two points. Since it works on the principle of no deflection, it is the most accurate method known. When a cell is connected to the circuit in order to obtain its EMF, a jockey is slid on the potentiometer wire to obtain a null point.

This null point is the length when multiplied by the potential gradient of the wire (potential per unit length), which gives the EMF of the unknown cell. By increasing the length of its wire, the potential gradient across it can be decreased, thus making the instrument more sensitive.