




Essential Experiment: Understanding Internal Resistance Measurement for CBSE Class 12 Physics 2025-26
A uniform wire AB with a low temperature coefficient of resistance is stretched over a uniform wooden scale to make a potentiometer. The potentiometer's wire is organised into two or three rows, summing to about $400\,cm$. Typically, a wooden board with a $100\,cm$ scale is fastened next to it.
The cell produces EMF, i.e. Electromotive Force. This is the energy it provides to the electrons of the conductor by setting up an electric potential. Due to this, the electrons are able to drift and thus are able to produce an electric current. However, other than the resistance provided by the constituent atoms of the conductor, the cell also provides some resistance. This is known as the internal resistance of the cell.
Table of Contents
Aim
Apparatus Required
Theory
Procedure
Observations
Result
Precautions
Lab Manual Questions
Viva Questions
Practical Based Questions
Aim
To set up a potentiometer and use it to determine the internal resistance of a given primary cell using potentiometer
Apparatus Required
Potentiometer
Battery (or battery eliminator)
Two one-way keys
Rheostat of low resistance
Galvanometer
High resistance box
Fractional resistance box
Ammeter
Voltmeter
Cell
Jockey
Set square
Connecting wires
Sand paper
Theory
The device works on the principle that when two points are at the same potential, no current flows through the wire connecting those points. To use the device, a potential is set across the wire of the potentiometer. Each unit length of the potentiometer has a certain potential, known as the potential gradient. It can mathematically be expressed as $\text{Potential gradient} = \dfrac{\text{Potential across potentiometer wire}}{\text{Total length of potentiometer wire}}$.
The potentiometer wire is an external resistance in the circuit. In the absence of an external resistance, a closed circuit is short-circuited. This can be calculated from the equation $V = E - Ir$, ……..(1)
Where $V$ is potential difference, $E$ is EMF of the cell, $I$ is the current through circuit and $r$ is the internal resistance. By putting the value of $I = \dfrac{E}{r}$ in (1), we get $V=0$
Similarly, if the terminals of cell are not connected, it is an open circuit and the potential difference across this cell is equal to its EMF as $I=0$ (from 1)
But, if an external resistance $R$ is connected in the circuit, then equation (1) becomes $V = E - \left ( \dfrac{E}{R+r} \right )r$ ….(2)
Rearranging (2), we get $\dfrac{E}{V}= 1 + \dfrac{r}{R}$ …(3)
When the jockey connected to one end of the cell of unknown internal resistance is slid over the potentiometer wire, it tries to balance the EMF of the cell with the potential of the wire. As soon as the length of the potentiometer to suffice the EMF of the cell is reached, the galvanometer shows no deflection. Thus the null point is said to be obtained. This way $V$ as well as $E$ can be obtained by arranging the circuit accordingly.
Mathematically, EMF of cell $(E)$ or potential across cell $V$ and length of potentiometer wire $(L)$ can be related as $E = k \times L_0$ or $V = k \times L$
Where, $k$ is the potential gradient of the potentiometer wire.
Now, we can write the ratio of $E$ and $V$ in terms of the length of the null point as $\dfrac{E}{V}=\dfrac{L_0}{L}$.
Therefore, equation (3) becomes $\dfrac{L_0}{L} = 1 + \dfrac{r}{R}$
Or, $\dfrac {L_0 – L}{L} = \dfrac{r}{R}$
Therefore, internal resistance of cell can be calculated by $r = \left ( \dfrac{L_0-L}{L} \right )R$
Procedure
Connect the circuit as shown in the diagram. In the diagram, $E_1$ is the cell of unknown internal resistance $(r)$ and $E$ is the cell providing potential difference to the potentiometer circuit.
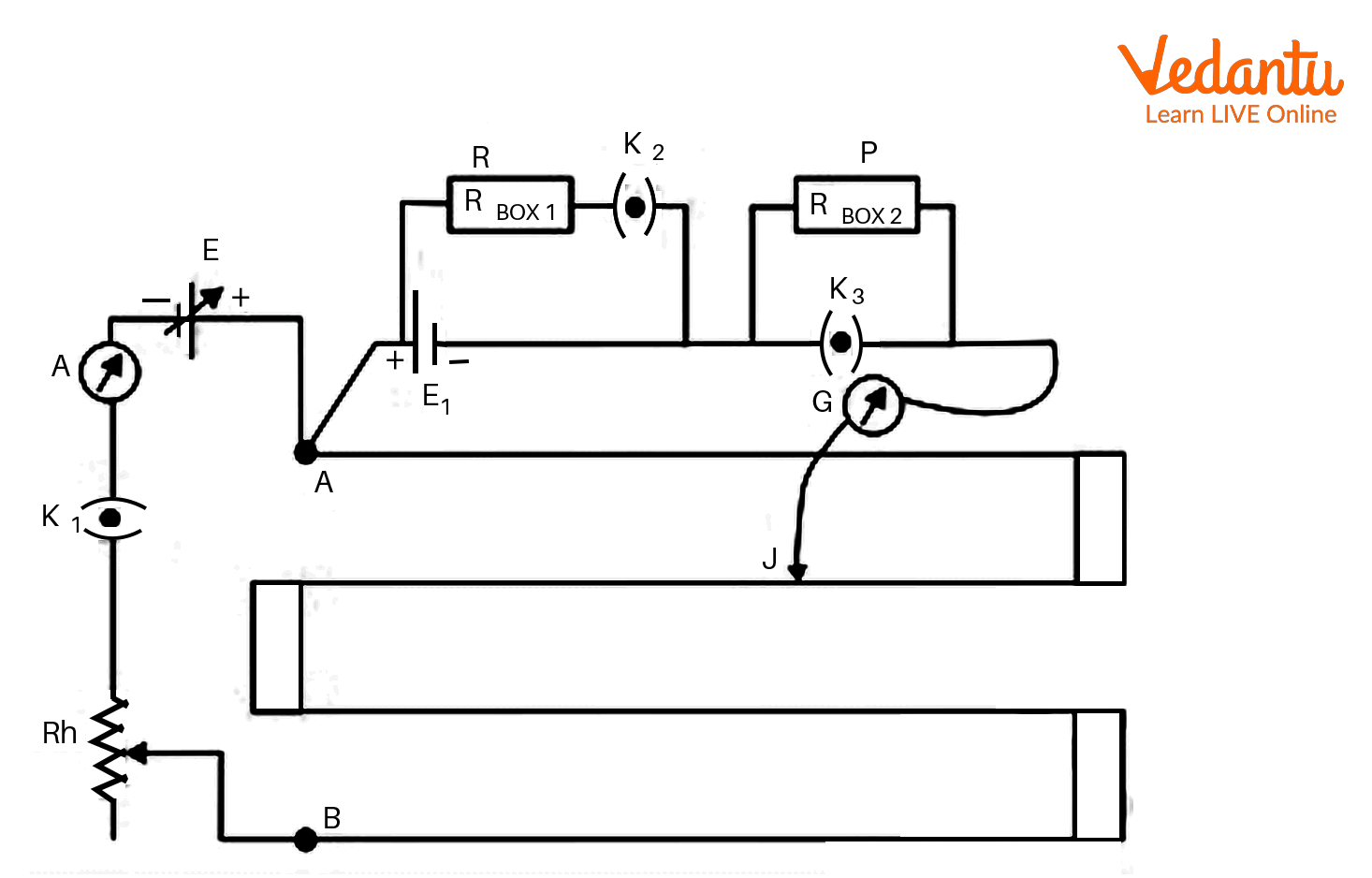
Circuit diagram
After checking the connection, insert a plug in key $K_1$ to connect the potentiometer circuit.
Keep the keys $K_2$ and $K_3$ open so that $R_{BOX-1}$ is not in the circuit whereas $R_{BOX-2}$ is. Take out a protective resistance from $R_{BOX-2}$.
Now, insert a plug in key $K_3$ to short circuit $R_{BOX-2}$ and find the balance length $L_0$ using a jockey.
Take $R=10 \Omega$ from $R_{BOX-1}$ and close the key $K_2$ to include $R_{BOX-1}$ into the circuit. With this set up, quickly measure balance length $L$ and then pull the plug so that $K_2$ is open again.
Throughout the above observations, keep the ammeter reading constant.
Reduce the value of resistance $R$ from $R_{BOX-1}$ in equal increments of $1 \, \Omega$ and get the balance length $L$ for each value of $R$.
Find the value of $L_0$ by opening $K_2$ and repeating step 4.
Observations
Observation Table
Calculate the value of internal resistance $(r)$ using the formula $ r \ = \left ( \dfrac{L_0-L}{L} \right )R$ for each set of observations. Find the mean of the internal resistance $(r)$.
Calculate the value of $r$ using a graph as well-
The equation $r= \left ( \dfrac{L_0-L}{L} \right )R$ can be rearranged to $\dfrac{1}{R}=\dfrac{L_0}{r}\left ( \dfrac{1}{L} \right )- \dfrac{1}{r}$ .
Plot a graph of $\dfrac{1}{R}$ versus $\dfrac{1}{L}$. The graph will come out to be a straight line graph having slope $\dfrac{L_0}{r}$.
Extend the slope to find the intercept. This intercept will give a value of $\dfrac{1}{r}$, which can be reciprocated to obtain the value of internal resistance $(r)$.
Result
The internal resistance $(r)$ of the cell according to mean value is …………….
The internal resistance $(r)$ of the cell according to the graph is …………….
Precautions
It is important to avoid disturbing the primary cell of unknown internal resistance, since doing so might alter the accuracy of its internal resistance.
The primary cell, $E_1$, should have a higher EMF than battery $E$.
Positive terminals of both cells $E$ and $E_1$ both should be connected to the same point on the potentiometer.
Always measure distance up to the balancing point starting from end A on the potentiometer, which is the location where the positive terminals of the battery are attached.
Lab Manual Questions
1. The potential difference is measured using a voltmeter connected in series with a battery's terminals. What distinguishes it from emf?
Ans: A voltmeter can only measure the difference in voltage between a cell's two terminals. However, it adds some resistance to the circuit. Therefore, it takes up some current and shows potential less than the actual EMF.
2. What conclusions would you draw if the galvanometer needle in your test setup kept swaying?
Ans: This may be due to error in connections. All connections should be checked and tightened.
3. Find the internal resistance of a freshly prepared Leclanche cell. Does its internal resistance change with $R$ ?
Ans: The internal resistance of a cell is independent of the external resistance $R$ connected. It only depends on the concentration of electrolyte, the temperature and the distance between electrodes.
4. State the factors on which the internal resistance of a cell depends.
Ans: The concentration of electrolyte, the temperature and the distance between electrodes of the cell affects the internal resistance of a cell.
Viva Questions
1. Explain what is the internal resistance of a cell?
Ans: It is the resistance provided by the cell, against the flow of current.
2. What is a potentiometer and state its uses?
Ans: Potentiometer is a device having a long wire attached, across which a potential gradient is set up. It is used to measure the EMF and internal resistance of a cell.
3. What is the difference between the Voltage across a cell when it is connected to an external resistance and when it’s not?
Ans: The potential difference $V$, the EMF of cell $E$, the internal resistance $r$ and the current $I$ can be related by the equation $V = E - Ir$. When there is no external resistance connected, by Ohm’s law the current $I = \dfrac{E}{r}$. Adding this value in the first equation, $V = E - \dfrac{E}{r}r$. Therefore, $V= 0$. However, in the presence of external resistance, $I = \dfrac{E}{R+r}$. Therefore, $V = E - \dfrac{E}{R+r}r$. Therefore, $V = \dfrac{ER}{R+r}$
4. What is the preferred substance for making a potentiometer wire?
Ans: The wire used in potentiometers is typically constructed of an alloy, such as manganin or nichrome. This is due to the high resistivity and low temperature coefficient of resistance of such alloys.
5. How does the internal resistance of a cell depend on current drawn from it?
Ans: A cell's internal resistance is independent of the current that is being drawn from it. Internal resistance depends on the type of the electrolyte and is independent of current because it is just the amount of resistance the cell's electrolyte offers to the flow of electric current. However, it increases with increase in temperature and temperature increases due to heat generated by the flowing current.
6. What factors affect the internal resistance of a cell?
Ans: The concentration of electrolyte, the temperature and the distance between electrodes of the cell affects the internal resistance of a cell.
7. State the possible sources of error in the experiment.
Ans: The possible sources of error are as follows:
The cross-section of a potentiometer wire need not be uniform.
The resistance of the brass strips at their ends might be limited.
The auxiliary battery's emf, which causes the potential drop down the wire, could vary over the duration of the experiment.
Some mistake may be introduced if the potentiometer wire is heated by current.
8. What is a rheostat?
Ans: A rheostat is an adjustable resistor used in situations where varying resistance or adjusting current in an electric circuit is necessary.
9. Why does a galvanometer show no deflection at the null point?
Ans: The potential of both the terminals to which the galvanometer is connected is the same and thus there is no potential difference at the null point. Thus, no current flows and the galvanometer needle does not deflect.
10. What are the voltmeter and ammeter used for?
Ans: The voltmeter is connected in parallel to the resistance, the voltage or potential difference across which is to be measured. The ammeter, on the other hand, is connected in series with the resistance the current flowing through which is to be measured.
Practical Based Questions
The internal resistance of which among the following cannot be calculated
Leclanche cell
Daniel cell
Nickel metal Hydride
Dry cell
Ans: (c)
The current $(I)$ flowing through a cell of EMF $E$ and internal resistance $r$ when it is connected to an external resistance $R$ is:
$\dfrac{E}{R+r}$ Coulomb
$0$ Coulomb
$\dfrac{R+r}{E}$ Coulomb
Infinite
Ans: (a)
The potential across a cell of EMF $E$ and internal resistance $r$ is:
Infinite
$E$
$\dfrac{E}{r}$
Zero
Ans: (d)
The current $(I)$ flowing through a cell of EMF $E$ and internal resistance $r$ is:
$0$ Coulomb
$\dfrac{E}{r}$ Coulomb
$\dfrac{r}{E}$ Coulomb
Infinite
Ans: (b)
Potential gradient of potentiometer wire depends on
Current passing through the potentiometer wire
Resistivity of material of the potentiometer wire
Area of cross-section of the potentiometer wire
All of the above
Ans: (d)
The sensitivity of the potentiometer can be increased by:
Decreasing the thickness of the potentiometer wire
Increasing the length of the potentiometer wire
Increasing the temperature of the surrounding
All of the above
Ans: (b)
Which instrument is used to measure deflection due to current:
Voltmeter
Rheostat
Galvanometer
Keys
Ans: (c)
Which value cannot be measured by a potentiometer?
Capacity
Resistance
Electric current
Potential
Ans: (a)
If the radius of the potentiometer wire is doubled, the length of the null point will
Remain same
Increase
Decrease
Increase and then decrease
Ans: (c)
If the length of the potentiometer wire is increased but same current is flowed through it, its sensitivity will:
Increase
Decrease
Remain constant
Cannot be predicted
Ans: (a)
Summary
A potentiometer works on the principle that when two points are at the same potential, no current flows through the wire connecting those two points. Since it works on the principle of no deflection, it is the most accurate method. A jockey is slid on the potentiometer wire to obtain a null point since the length of the null point is proportional to the EMF of cell $E_1$.
This method is repeated in the presence of external resistance to find the new potential across the cell. The null point is the length which, multiplied by the potential gradient of the wire (potential per unit length), gives the EMF $E$ of and potential $V$ across the cell. After the ratio of the length of the null point of $E$ and $V$ is found, it can be equated with their potentials. Therefore, $\dfrac{E}{V}=\dfrac{L_0}{L}$. This can then be used to find internal resistance of cell from formula $ r = \left ( \dfrac{L_0-L}{L} \right )R$
FAQs on Step-by-Step Guide to Measuring a Primary Cell's Internal Resistance Using a Potentiometer (2025-26)
1. What is the main principle behind determining the internal resistance of a cell using a potentiometer in Class 12 Physics exams?
The main principle is that no current flows between two points at the same potential. By adjusting the potentiometer, the length corresponding to this condition (null point) is found, allowing calculation of the cell’s EMF and terminal potential difference. The ratio of these lengths, with and without external resistance, helps determine the internal resistance using the category-important formula: r = ((L₀-L)/L) × R.
2. Which formula should you use to calculate the internal resistance of a primary cell in board practical exams, and why is each term significant?
The essential formula is r = ((L₀ - L)/L) × R, where:
- L₀: Balance length without external resistance
- L: Balance length with external resistance R
- R: Known external resistance in the circuit
3. What are the most common board exam mistakes when setting up the potentiometer experiment for internal resistance, and how can you avoid them?
Common mistakes include:
- Connecting positive terminals incorrectly
- Allowing heating of the potentiometer wire, which changes resistance
- Not keeping the current constant during observations
- Measuring length from the wrong end of the potentiometer
4. In board marking, why is it important to include both mean value and graphical methods when reporting the internal resistance result?
For maximum marks, examiners expect students to demonstrate understanding of both analytical (mean value) and graphical approaches. The mean value confirms consistency in measurements, while the graphical method (plotting 1/R vs 1/L) shows application of concepts and critical analysis—both are often noted in marking schemes for higher-order process skills.
5. How can variation in electrolyte concentration and electrode separation impact board answers on internal resistance, and why should these factors be discussed?
According to the CBSE syllabus, internal resistance depends on the concentration of the electrolyte, temperature, and electrode distance. Discussing these in your answer can fetch extra points for depth, showing you understand what conditions might affect your experimental results and the reliability of your findings.
6. What key precautions must be mentioned to secure full marks in a question on this experiment in CBSE boards?
Essential precautions include:
- Ensure uniform cross-section of potentiometer wire
- Connect both cells’ positive terminals to the same potentiometer end
- Do not disturb the primary cell during observations
- Always start measurement from point A
- Minimize current to prevent wire heating
7. Why does the potentiometer method yield more accurate results for EMF and internal resistance compared to using a voltmeter alone?
The potentiometer method does not draw any current from the cell when measuring EMF, so it gives the true value. In contrast, a voltmeter draws some current and shows a slightly less potential due to voltage drop across internal resistance—leading to less accurate results.
8. In high-weightage board questions, what reasoning should you provide if the galvanometer needle never stays at zero during the experiment?
This issue indicates incomplete balancing—most likely caused by loose or faulty connections, variable current in the wire, or defective cells. Addressing these points and suggesting to recheck connections or replace cells demonstrates conceptual understanding and earns method marks.
9. How can you justify the choice of material for the potentiometer wire in an exam answer, and what board-relevant keywords should be included?
The potentiometer wire is typically made from manganin or nichrome due to their high resistivity and low temperature coefficient. This ensures consistent potential gradient and reliable measurements—keywords expected in board marking guidelines.
10. If asked in the exam, how would you explain why the internal resistance of a cell does not depend on the external resistance (R) used?
The internal resistance is a property of the cell itself—determined by the electrolyte’s nature, temperature, and electrode configuration—not by the value of external resistance in the circuit. R only affects the terminal voltage, not the cell’s intrinsic resistance.
11. What is the significance of the null point in securing marks during the experiment, and how does it relate to accuracy?
The null point is where the galvanometer shows zero deflection, indicating equal potential. Accurately finding this point is crucial for correct calculation of EMF and internal resistance. Missing or misreading the null point leads to calculation errors and loss of marks in practical exams.
12. How does increasing the length of the potentiometer wire affect the sensitivity of the instrument and exam scoring?
Increasing the potentiometer wire's length enhances sensitivity, making it easier to detect small potential differences. This is an expected answer point for HOTS and application-based questions in the exam regarding potentiometer improvement tips.
























