CBSE Class 10 Maths Important Questions Chapter 5 - Arithmetic Progressions - Free PDF Download
1. The fourth term of an AP is zero. Prove that its \[{{25}^{th}}\] term is triple its \[{{11}^{th}}\] term.
Ans: Given that \[{{a}_{4}}=0~\]
\[\Rightarrow a+3d=0\]
\[\Rightarrow a=-3d\] …(1)
We have to prove that \[{{a}_{25}}=3{{a}_{11}}\]
\[\Rightarrow a+24d=3\left( a+10d \right)\]
\[\Rightarrow a+24d=3a+30d\]
From equation (1),
\[\Rightarrow -3d+24d=3\left( -3d \right)+30d\]
\[\Rightarrow 21d=21d\]
\[\therefore LHS=RHS\]
Hence proved.
2.Find the \[{{20}^{th}}\] term from the end of the AP \[3,8,13,...,253\].
Ans: Given AP \[3,8,13,...,253\]
Last term is \[253\]
\[{{a}_{20}}\] from end is \[I-(n-1)d\]
Putting the values we get,
\[\Rightarrow 253-(20-1)5\]
\[\Rightarrow 158\]
3.If the \[{{p}^{th}}\] , \[{{q}^{th}}\] and \[{{r}^{th}}\] term of an AP is \[x,y\] and \[z\] respectively, show that \[x\left( q-r \right)+y\left( r-p \right)+z\left( p-q \right)=0\] .
Ans: \[{{\text{p}}^{th}}\text{term}\Rightarrow x=A+\left( p-1 \right)D\]
\[{{q}^{th}}\text{term}\Rightarrow y=A+\left( q-1 \right)D\]
\[{{r}^{th}}\text{term}\Rightarrow z=A+\left( r-1 \right)D\]
We have to prove:
\[x\left( q-r \right)+y\left( r-p \right)+z\left( p-q \right)=0\]
\[\Rightarrow \left\{ A+\left( p-1 \right)D \right\}\left( q-r \right)+\left\{ A+\left( q-1 \right)D \right\}\left( r-p \right)~+\left\{ A+\left( r-1 \right)D \right\}\left( p-q \right)~=0\]
\[\Rightarrow A\left\{ \left( q-r \right)+\left( r-p \right)+\left( p-q \right) \right\}+D\{\left( p-1 \right)\left( q-r \right)~+\left( r-1 \right)\left( r-p \right)+\left( r-1 \right)\left( p-q \right)\}=0\]
\[\Rightarrow A\cdot 0+D\{p\left( q-r \right)+q\left( r-p \right)+r\left( p-q \right)-\left( q-r \right)\left( r-p \right)-\left( p-q \right)\}=0\]
\[\Rightarrow A\cdot 0+D\cdot 0=0\]
\[\therefore LHS=RHS\]
Hence proved.
4. Find the sum of first \[40\] positive integers divisible by \[6\] also find the sum of first \[20\] positive integers divisible by \[5\] or \[6\] .
Ans: Numbers which are divisible by \[6\] are \[6,12,18,...,240\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{40}}=\dfrac{40}{2}\left[ 12+39\left( 6 \right) \right]\]
\[\therefore {{S}_{40}}=4920\]
Numbers div by \[5\] or \[6\] are
\[30,60,...600\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{20}}=\dfrac{20}{2}\left[ 60+19\left( 30 \right) \right]\]
\[\therefore {{S}_{20}}=6300\]
5. A man arranges to pay a debt of Rs. \[3600\] in \[40\] monthly installments which are in an AP. When \[30\] installments are paid he dies leaving one-third of the debt unpaid. Find the value of the first installment.
Ans: Let the value of instalment be \[{{S}_{40}}=3600\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow \dfrac{40}{2}[2a+39d]=3600\]
\[\Rightarrow [2a+39d]=180\] …(1)
If thirtyinstallments are paid then,
\[\Rightarrow {{\text{S}}_{30}}=\dfrac{30}{2}[2a+29d]\]
\[\Rightarrow \dfrac{30}{2}[2a+29d]=\dfrac{2}{3}\times 3600\]
\[\Rightarrow 2a+29d=160\] …(2)
Solving equations (1) and (2) we get,
\[d=2\]
\[a=51\]
Therefore, the first instalment is \[Rs.51\] .
6. Find the sum of all three-digit numbers which leave remainder \[3\] when divided by \[5\].
Ans: Three-digit numbers which leave remainder \[3\] when divided by \[5\] are \[103,108,...,998\]
To find \[n\] ,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\Rightarrow 998=103+5\left( n-1 \right)\]
\[\therefore n=180\]
To find sum use the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{180}}=\dfrac{180}{2}\left[ 2\left( 103 \right)+5\left( 180-1 \right) \right]\]
\[\therefore {{S}_{180}}=99090\]
7.Find the value of \[x\] if \[2x+1,{{x}^{2}}+x+1,3{{x}^{2}}-3x+3\] are consecutive terms of an AP.
Ans: We know that consecutive terms of an AP have a same common difference
\[{{a}_{2}}\text{ }{{a}_{1}}=\text{ }{{a}_{3}}\text{ }{{a}_{2}}~\]
\[\Rightarrow {{x}^{2}}\text{+}x+1-2x-1=3{{x}^{2}}-3x+3-{{x}^{2}}-x-1\]
\[\Rightarrow {{x}^{2}}-3x+2=0~\]
\[\Rightarrow \left( x-1 \right)\left( x2 \right)=0\]
\[\therefore x=1,2\]
8. Raghav buys a shop for Rs. \[1,20,000\] . He pays half the balance of the amount in cash and agrees to pay the balance in \[12\] annual installments of Rs. \[5000\] each. If the rate of interest is \[12%\] and he pays with the installment the interest is due for the unpaid amount. Find the total cost of the shop.
Ans: Given that balance is Rs. \[60,000\] in \[12\]installments of Rs. \[5000\] each.
Amount of first instalment is \[5000+\left( \dfrac{12}{100}\times 60,000 \right)=12200\]
Amount of second instalment is \[5000+\left( \dfrac{12}{100}\times 55,000 \right)=11600\]
Amount of third instalment is \[5000+\left( \dfrac{12}{100}\times 50,000 \right)=11000\]
∴ AP is \[12200,11600,11000,...\]
Here, \[d=600\]
Cost of shop is = \[60,000\] + [sum of \[12\] instalment]
\[\Rightarrow 60,000+\dfrac{12}{2}[24,400-6600]=1,66,800\]
The total cost of the shop is Rs. \[1,66,800\] .
9. Prove that $ {{a}_{m+n}}+{{a}_{m-n}}=2{{a}_{m}} $ .
Ans: We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
Therefore,
\[{{a}_{m+n}}={{a}_{1}}+\left( m+n-1 \right)d\] …(1)
\[{{a}_{m-n}}={{a}_{1}}+\left( m-n-1 \right)d\] …(2)
\[{{a}_{m}}={{a}_{1}}+\left( m-1 \right)d\] …(3)
Adding equations (1) and (2),
\[{{a}_{m+n}}+{{a}_{m-n}}={{a}_{1}}+\left( m+n-1 \right)d+{{a}_{1}}+\left( m-n-1 \right)d\]
\[{{a}_{m+n}}+{{a}_{m-n}}=2[{{a}_{1}}+\left( m-1 \right)d]~\]
From equation (3) we can conclude that,
\[{{a}_{m+n}}+{{a}_{m-n}}=2{{a}_{m}}\]
Hence proved.
10. If the roots of the equation $ (b-c){{x}^{2}}+(c-a)x+(a-b)=0 $ are equal show that \[a,b,c\] are in A.P
Ans: If the roots of the equation \[a{{x}^{2}}+bx+c=0\] are equal then,
\[{{b}^{2}}-4ac=0\]
Therefore, for equation $ (b-c){{x}^{2}}+(c-a)x+(a-b)=0 $
\[\Rightarrow {{\left( c-a \right)}^{2}}-4\left( b-c \right)\left( a-b \right)=0\]
\[\Rightarrow {{c}^{2}}+{{a}^{2}}-2ca-4\left( ab-{{b}^{2}}-ca+cb \right)=0\]
\[\Rightarrow {{c}^{2}}+{{a}^{2}}+4{{b}^{2}}+2ca-4ba-4bc=0\]
\[\Rightarrow {{\left( a-2b+c \right)}^{2}}=0\]
\[\Rightarrow \left( a-2b+c \right)=0\]
\[\therefore \left( a+c \right)=2b\]
Hence proved that \[a,b,c\] are in AP.
11. Balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second two balls, and so on. If \[669\] more balls are added, then all the balls can be arranged in the shape of a square and each of its sides then contains \[8\] balls less than each side of the triangle. Find the initial number of balls.
Ans: Let there be \[n\] balls in each side of the triangle
∴ No. of ball (in ∆),
\[1+2+3+...=\dfrac{n\left( n+1 \right)}{2}\]
No. of balls in each side square is \[n-8\]
No. of balls in square is \[{{\left( n-8 \right)}^{2}}\]
From the given data,
\[\dfrac{n\left( n+1 \right)}{2}+669={{\left( n-8 \right)}^{2}}\]
\[\Rightarrow {{n}^{2}}+n+1338=2({{n}^{2}}-16n+64)\]
\[\Rightarrow {{n}^{2}}-33n-1210=0\]
\[\Rightarrow \left( n-55 \right)\left( n+22 \right)=0\]
\[\Rightarrow n=55,-22\]
Negative number is not possible,
Number of balls is \[55\] .
12. Find the sum of $ \left( 1-\dfrac{1}{n} \right)+\left( 1-\dfrac{2}{n} \right)+\left( 1-\dfrac{3}{n} \right)+...nterms $ .
Ans: We have to find sum of $ \left( 1-\dfrac{1}{n} \right)+\left( 1-\dfrac{2}{n} \right)+\left( 1-\dfrac{3}{n} \right)+...nterms $
$ \Rightarrow \left[ 1+1+...nterms \right]-\left[ \left( \dfrac{1}{n} \right)+\left( \dfrac{2}{n} \right)+\left( \dfrac{3}{n} \right)+...nterms \right] $
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{n}}=n-\dfrac{n}{2}\left[ 2\left( \dfrac{1}{n} \right)+\left( n-1 \right)\left( \dfrac{1}{n} \right) \right]\]
\[\Rightarrow {{S}_{n}}=n-1-\dfrac{n}{2}+\dfrac{1}{2}\]
\[\therefore {{S}_{n}}=\dfrac{n-1}{2}\]
13. If the following terms form a AP. Find the common difference & write the next \[3\] terms \[3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2},...\]
Ans: Common difference is \[d=3+\sqrt{2}-3\]
\[\therefore d=\sqrt{2}\]
Next three terms are $ 3+4\sqrt{2},3+5\sqrt{2},3+6\sqrt{2}.... $
14. Find the sum of \[a+b,a-b,a-3b,...22terms\] .
Ans: Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{22}}=\dfrac{22}{2}\left[ 2\left( a+b \right)+\left( 22-1 \right)\left( -2b \right) \right]\]
\[\Rightarrow {{S}_{22}}=11\left[ 2a-40b \right]\]
\[\therefore {{S}_{22}}=22a-440b\]
15. Write the next two terms \[\sqrt{12,}\sqrt{27},\sqrt{48},\sqrt{75},...\]
Ans: Here, \[a=\sqrt{12}\] and
\[d=\sqrt{27}-\sqrt{12}\]
\[\Rightarrow d=3\sqrt{3}-2\sqrt{3}\]
\[\therefore d=\sqrt{3}\]
Next two terms are $ \sqrt{108},\sqrt{147} $
16. If the \[{{p}^{th}}\] term of an AP is \[q\] and the \[{{q}^{th}}\] term is \[p\] . P.T its \[{{n}^{th}}\] term is \[p+q-n\] .
Ans: Given that
\[{{a}_{p}}=q\]
\[\Rightarrow a+\left( p-1 \right)d=q\] …(1)
\[{{a}_{q}}=p\]
\[\Rightarrow a+\left( q-1 \right)d=p\] …(2)
From equations (1) and (2),
\[\Rightarrow d\left[ pq \right]=qp\text{ }\]
\[\therefore d=-1\]
Putting it in equation (1) we get,
\[a=q+p-1~\]
We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\Rightarrow {{a}_{n}}=\left( q+p1 \right)-1\left( n1 \right)\]
\[\therefore {{a}_{n}}=\left( q+p-n \right)\]
Hence proved.
17. If $ \dfrac{1}{x+2},\dfrac{1}{x+3},\dfrac{1}{x+5} $ are in AP find \[x\] .
Ans: We have to find \[x\] if $ \dfrac{1}{x+2},\dfrac{1}{x+3},\dfrac{1}{x+5} $ are in AP.
\[\Rightarrow \dfrac{1}{x+2}+\dfrac{1}{x+5}=\dfrac{2}{\left( x+3 \right)}\]
\[\Rightarrow \dfrac{2x+7}{{{x}^{2}}+7x+10}=\dfrac{2}{x+3}\]
\[\Rightarrow \left( 2x+7 \right)\left( x+3 \right)=2\left( {{x}^{2}}+7x+10 \right)\]
\[\Rightarrow \left( 2{{x}^{2}}+13x+21 \right)=\left( 2{{x}^{2}}+14x+20 \right)\]
\[\therefore x=1\]
18. Find the middle term of the AP \[1,8,15,...,505\] .
Ans: Total number of terms,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\Rightarrow 505=1+7\left( n-1 \right)\]
\[\therefore n=73\]
\[\therefore n=36,37\] are middle terms
\[{{a}_{36}}=1+7\left( 36-1 \right)\]
\[\therefore {{a}_{36}}=246\] and
\[{{a}_{37}}=253\]
19. Find the common difference of an AP whose first term is \[100\] and the sum of whose first \[6\] terms is \[5\] times the sum of next \[6\] terms.
Ans: Here \[a=100\] and
\[{{a}_{1}}+{{a}_{2}}+...+{{a}_{6}}=5({{a}_{7}}+\ldots +{{a}_{12}})~\]
\[\Rightarrow 6\left( \dfrac{{{a}_{1}}+{{a}_{6}}}{2} \right)=5\times 6\left( \dfrac{{{a}_{7}}+{{a}_{12}}}{2} \right)\]
\[\Rightarrow a+a+5d=5\left[ a+6d+a+11d \right]\]
\[\Rightarrow 800+80d=0\]
\[\therefore d=-10\]
20. Find the sum of all natural no. between \[101\] and \[304\] which are divisible by \[3\] or \[5\] . Find their sum.
Ans: The AP formed by numbers that are divisible by \[3\] or \[5\] is
\[105,120,135,....300\]
The sum of this AP is:
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{14}}=\dfrac{14}{2}\left[ 300+13\left( 15 \right) \right]\]
\[\Rightarrow {{S}_{14}}=19035\]
21. The ratio of the sum of first \[n\] terms of two AP’s is \[7n+1:4n+27\] . Find the ratio of their \[{{11}^{th}}\] terms.
Ans: Using the formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\dfrac{\dfrac{m}{2}\left[ 2{{a}_{1}}+(n-1){{d}_{1}} \right]}{\dfrac{m}{2}\left[ 2{{a}_{2}}+(n-1){{d}_{2}} \right]}=\dfrac{7n+1}{4n+27}\]
\[\Rightarrow \dfrac{2{{a}_{1}}+(n-1){{d}_{1}}}{2{{a}_{2}}+(n-1){{d}_{2}}}=\dfrac{7n+1}{4n+27}\]
Here \[n=21\] ,
\[\Rightarrow \dfrac{2{{a}_{1}}+20{{d}_{1}}}{2{{a}_{2}}+20{{d}_{2}}}=\dfrac{7\times 21+1}{4(21)+27}\]
\[\Rightarrow \dfrac{{{a}_{1}}+10{{d}_{1}}}{{{a}_{2}}+10{{d}_{2}}}=\dfrac{148}{111}\]
\[\therefore \dfrac{{{a}_{1}}+10{{d}_{1}}}{{{a}_{2}}+10{{d}_{2}}}=\dfrac{4}{3}\]
Ratio of their \[{{11}^{th}}\] terms is \[4:3\]
22. If there are \[2n+1\] terms in an AP, prove that the ratio of the sum of odd terms and the sum of even terms is \[n+1:n\] .
Ans: Use the formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Sum of odd terms:
\[{{s}_{1}}=\text{ }{{a}_{1}}+\text{ }{{a}_{3}}+\text{ }\ldots \ldots \ldots \text{ }{{a}_{2n+1}}\]
\[{{s}_{1}}=\dfrac{n+1}{2}[2{{a}_{1}}+2nd]\]
\[\therefore {{s}_{1}}=\left( n+1 \right)\left( a+nd \right)~\]
Sum of even terms:
\[{{s}_{2}}=\text{ }{{a}_{2}}+\text{ }{{a}_{4}}+\text{ }\ldots ..\text{ }{{a}_{2n}}~\]
$ {{s}_{2}}=\dfrac{n}{2}[a+d+a+(2n-1)d] $
\[\therefore {{s}_{2}}=n[a+nd]\]
\[\therefore \dfrac{{{s}_{1}}}{{{s}_{2}}}=\dfrac{(n+1)(a+nd)}{n(a+nd)}\]
\[\therefore \dfrac{{{s}_{1}}}{{{s}_{2}}}=\dfrac{(n+1)}{n}\]
23. Find the sum of all natural numbers amongst the first one thousand numbers which are neither divisible \[2\] nor by \[5\].
Ans: Sum of all natural numbers in first thousand integers which are not divisible by two i.e. sum of odd integers.
1 + 3 + 5 + ………. + 999
n = 500
$ {{S}_{500}}=\dfrac{500}{2}[1+999] $
$ \therefore {{S}_{500}}=250000 $
Odd No’s which are divisible by five
5 + 15 + 25 …….. + 995
n = 100
$ {{S}_{100}}=\dfrac{100}{2}[5+995] $
$ \therefore {{S}_{100}}=50000 $
Required sum is $ 250000-50000=20,000 $
Very Short Answer Questions (1 Mark)
1. The next term of the AP in $ {{1}^{2}},{{5}^{2}},{{7}^{2}},73,.... $ is
$ 97 $
$ 92 $
$ 99 $
$ 95 $
Ans: (a) $ 97 $
2. The \[{{10}^{th}}\] term of the AP in \[2,7,12,...\] is
\[45\]
\[47\]
\[48\]
\[50\]
Ans: (b) \[47\]
3. If the sum of the circumferences of two circles with radii \[{{R}_{1}}\] and \[{{R}_{2}}\] is equal to the circumference of a circle of Radius, then \[R\]
\[{{R}_{1}}+{{R}_{2}}=R\]
\[{{R}_{1}}+{{R}_{2}}>R\]
\[{{R}_{1}}+{{R}_{2}}<R\]
None of these
Ans: (a) \[{{R}_{1}}+{{R}_{2}}=R\]
4. If the perimeter of a circle is equal to that of a square, then the ratio of their area is
\[22:7\]
\[14:11\]
\[7:22\]
\[11:14\]
Ans: (b) \[14:11\]
5. Area of a sector of angle \[{{p}^{\circ }}\] of a circle with radius \[R\] is
\[\dfrac{P}{100}\times 2\pi R\]
\[\dfrac{P}{180}\times \pi {{R}^{2}}\]
\[\dfrac{P}{360}\times 2\pi R\]
\[\dfrac{P}{720}\times 2\pi {{R}^{2}}\]
Ans: (d) \[\dfrac{P}{720}\times 2\pi {{R}^{2}}\]
6. Area of the sector of angle \[{{60}^{\circ }}\] of a circle with radius \[10\] cm is
\[52\dfrac{5}{21}c{{m}^{2}}\]
\[52\dfrac{8}{21}c{{m}^{2}}\]
\[52\dfrac{4}{21}c{{m}^{2}}\]
none of there
Ans: (b) \[52\dfrac{8}{21}c{{m}^{2}}\]
7. \[{{11}^{th}}\] term of the AP \[-3,-\dfrac{1}{2},2,....\] is
\[28\]
\[22\]
\[-38\]
\[-48\dfrac{1}{2}\]
Ans: (b) \[22\]
8. If \[{{17}^{th}}\] term of an AP exceeds its \[{{10}^{th}}\] term by \[7\] . The common difference is
\[2\]
\[-1\]
\[3\]
\[1\]
Ans: (d) \[1\]
9. Which of the following list of no. form an AP?
\[2,4,8,16,...\]
\[2,\dfrac{5}{2},3,\dfrac{7}{2},...\]
\[0.2,0.22,0.222,...\]
\[1,3,9,27,...\]
Ans: (b) \[2,\dfrac{5}{2},3,\dfrac{7}{2},...\]
10. The \[{{n}^{th}}\] term of the AP in \[2,5,8,...\] is
\[3n-1\]
\[2n-1\]
\[3n-2\]
\[2n-3\]
Ans: (a) \[3n-1\]
11. If \[a,(a-2),3a\] are in AP, then value of \[a\] is
\[-3\]
\[-2\]
\[3\]
\[2\]
Ans: (b) \[-2\]
12. The sum of first \[n\] positive integers is given by
\[\dfrac{n(n-1)}{2}\]
\[\dfrac{n(2n+1)}{2}\]
\[\dfrac{n(n+1)}{2}\]
none of these
Ans: (c) \[\dfrac{n(n+1)}{2}\]
Short Answer Questions (2 Marks)
1. Find the missing variable from \[a,d,n\] and \[{{a}_{n}}\] , where \[a\] is the first term, \[d\] is the common difference and \[{{a}_{n}}\] is the \[{{n}^{th}}\] term of AP.
(i). \[a=7,d=3,n=8\]
Ans: (i) \[a=7,d=3,n=8\]
We need to find \[{{a}_{n}}\] here.
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[{{a}_{8}}=7+3\left( 8-1 \right)\]
\[\therefore {{a}_{8}}=28\]
(ii). \[a=-18,n=10,{{a}_{n}}=0\]
Ans: (ii) \[a=-18,n=10,{{a}_{n}}=0\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[0=-18+d\left( 10-1 \right)\]
\[\therefore d=2\]
(iii). \[d=-3,n=18,{{a}_{n}}=-5\]
Ans: (iii) \[d=-3,n=18,{{a}_{n}}=-5\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[-5=a-3\left( 18-1 \right)\]
\[\therefore a=46\]
(iv). \[a=-18.9,d=2.5,{{a}_{n}}=3.6\]
Ans: (iv) \[a=-18.9,d=2.5,{{a}_{n}}=3.6\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[3.6=-18.9+2.5\left( n-1 \right)\]
\[\therefore n=10\]
(v). \[a=3.5,d=0,n=105\]
Ans: (v) \[a=3.5,d=0,n=105\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[{{a}_{n}}=3.5+0\left( 105-1 \right)\]
\[\therefore {{a}_{n}}=3.5\]
2. Choose the correct choice in the following and justify:
(i). \[{{30}^{th}}\] term of the AP: \[10,7,4,...\] is
\[97\]
\[77\]
\[-77\]
\[-87\]
Ans: (i) Given AP \[10,7,4,...\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[{{a}_{30}}=10-3\left( 29 \right)\]
\[\therefore {{a}_{30}}=-77\]
Therefore, the answer is (C).
(ii). \[{{11}^{th}}\] term of the AP: \[-3,-\dfrac{1}{2},2,...\] is
\[28\]
\[22\]
\[-38\]
\[-48\dfrac{1}{2}\]
Ans: (ii) Given AP \[-3,-\dfrac{1}{2},2,...\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[{{a}_{11}}=-3-2.5\left( 11-1 \right)\]
\[\therefore {{a}_{11}}=22\]
Therefore, the answer is (B).
3. Which term of the AP: \[3,8,13,18,...\] is \[78\] ?
Ans: Here, \[a=3,d=5,{{a}_{n}}=78\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[78=3+5\left( n-1 \right)\]
\[\therefore n=16\]
It means \[{{16}^{th}}\] term of the given AP is equal to \[78\] .
4. Find the number of terms in each of the following APs:
(i). \[7,13,19,...,205\]
Ans: (i) Here, \[a=7,d=6,{{a}_{n}}=205\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[205=7+6\left( n-1 \right)\]
\[\therefore n=34\]
Therefore, there are \[34\] terms in the given arithmetic progression.
(ii). \[18,15\dfrac{1}{2},13,...,-47\]
Ans: (ii) Here, \[a=18,d=-2.5,{{a}_{n}}=-47\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[-47=18-2.5\left( n-1 \right)\]
\[\therefore n=26\]
Therefore, there are \[26\] terms in the given arithmetic progression.
5. Check whether \[-150\] is a term of the AP: \[11,,8,5,2,...\]
Ans: Here, \[a=11,d=-3,{{a}_{n}}=-150\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[-150=11-3\left( n-1 \right)\]
\[\therefore n=\dfrac{164}{3}\]
But, \[n\] cannot be in fraction.
Therefore, our supposition is wrong. \[-150\] cannot be a term in AP.
6. An AP consists of \[50\] terms of which \[{{3}^{rd}}\] term is \[12\] and the last term is \[106\] . Find the \[{{29}^{th}}\] term.
Ans: Given that
\[{{a}_{3}}=12\] and \[{{a}_{50}}=106\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 12=a+2d\] …(1)
\[\Rightarrow 106=a+49d\] …(2)
\[\Rightarrow a=106-49d\] …(3)
These are equations consisting of two variables.
Putting value of \[a\] in the equation (1),
\[12=106-49d+2d\]
\[\Rightarrow d=2\]
Putting it in equation (3),
\[\Rightarrow a=10649\left( 2 \right)\]
\[\therefore a=8\]
Therefore, First term is \[a=8\] and Common difference is \[d=2\]
To find \[{{29}^{th}}\] term use the formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow {{a}_{29}}=8+2\left( 29-1 \right)\]
\[\therefore {{a}_{29}}=64\]
7. How many multiples of \[4\] lie between \[10\] and \[250\]?
Ans: Given AP \[12,16,20,...,248\]
Here, \[a=12,d=4,{{a}_{n}}=248\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[248=12+4\left( n-1 \right)\]
\[\therefore n=60\]
Therefore, sixty multiples of \[4\] lie between \[10\] and \[250\] .
8. Which term of the AP: \[121,117,113,...\] is its first negative term?
Ans: Given AP: \[121,117,113,...\]
Here, \[a=121,d=117-121=-4\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow {{a}_{n}}=121-4\left( n-1 \right)\]
\[\Rightarrow {{a}_{n}}=125-4n\]
For the first negative term, \[{{a}_{n}}<0\]
\[\Rightarrow 125-4n<0\]
\[\Rightarrow n>\dfrac{125}{4}\]
\[\Rightarrow n>31\dfrac{1}{4}\]
\[n\] is an integer and \[n>31\dfrac{1}{4}\]
Hence, the first negative term is \[{{32}^{nd}}\] term
9. The sum of the third and the seventh terms of an AP is \[6\] and their product is \[8\]. Find the sum of sixteen terms of the AP.
Ans: Let the AP be \[a-4d,a-3d,a-2d,a-d,a,a+d,a+2d,a+3d,...\]
Then,
\[{{a}_{3}}=a-2d,{{a}_{7}}=a+2d\]
\[\Rightarrow {{a}_{3}}+{{a}_{7}}=a-2d+a+2d=6\]
\[\Rightarrow a=3\] …(1)
Also,
\[(a-2d)(a+2d)=8\]
\[\Rightarrow {{a}^{2}}-4{{d}^{2}}=8\]
From (1),
\[\Rightarrow {{d}^{2}}=\dfrac{1}{4}\]
\[\therefore d=\pm \dfrac{1}{2}\]
Taking \[d=\dfrac{1}{2}\] ,
\[{{S}_{16}}=\dfrac{16}{2}[2\times (a-4d)+(16-1)d]\]
\[\Rightarrow {{S}_{16}}=\dfrac{16}{2}\left[ 2\times \left( 3-4\left( \dfrac{1}{2} \right) \right)+(16-1)\left( \dfrac{1}{2} \right) \right]\]
\[\therefore {{S}_{16}}=76\]
Taking \[d=-\dfrac{1}{2}\] ,
\[{{S}_{16}}=\dfrac{16}{2}[2\times (a-4d)+(16-1)d]\]
\[\Rightarrow {{S}_{16}}=\dfrac{16}{2}\left[ 2\times \left( 3-4\left( -\dfrac{1}{2} \right) \right)+(16-1)\left( -\dfrac{1}{2} \right) \right]\]
\[\therefore {{S}_{16}}=20\]
The sum of sixteen terms of the AP is \[{{S}_{16}}=20\]or \[{{S}_{16}}=76\]
10. A ladder has rungs \[25\] cm apart (see figure). The rungs decrease uniformly in length from \[45\] cm, at the bottom to \[25\] cm at the top. If the top and the bottom rungs are \[2\dfrac{1}{2}\] m apart, what is the length of the wood required for the rungs?
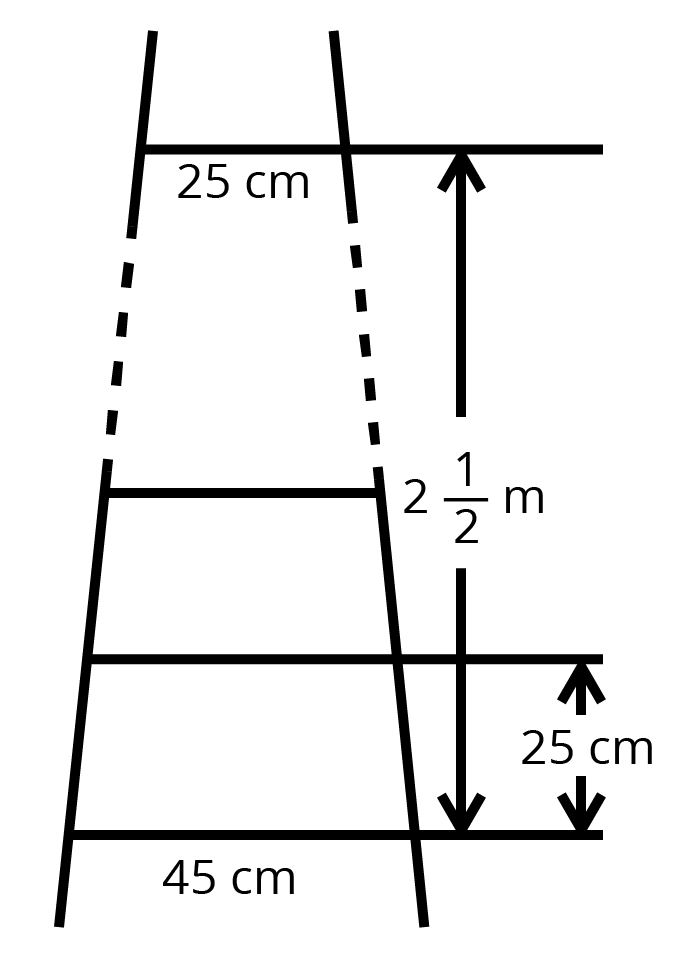
Ans: Number of rungs, \[(n)=\dfrac{2\dfrac{1}{2}\times 100}{25}\]
\[n=10\]
The length of the wood required for rungs = sum of ten rungs
\[\Rightarrow \dfrac{10}{2}\left[ 25+45 \right]=350cm\]
11. The houses of a row are numbered consecutively from \[1\] to \[49\]. Show that there is a value of \[x\] such that the sum of the numbers of the houses preceding the house numbered \[x\] is equal to the sum of the numbers of the houses following it. Find this value of \[x\] .
Ans: Here \[a=1,d=1\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{x-1}}=\dfrac{x-1}{2}[2\times 1+(x-1-1)\times 1]\]
\[\Rightarrow {{S}_{x-1}}=\dfrac{{{x}^{2}}-x}{2}\]
\[{{S}_{x}}=\dfrac{x}{2}\left[ 2\times 1+(x-1)\times 1 \right]\]
\[\Rightarrow {{S}_{x}}=\dfrac{{{x}^{2}}+x}{2}\]
Now, \[{{S}_{49}}=\dfrac{49}{2}[2\times 1+(49-1)\times 1]\]
\[\Rightarrow {{S}_{49}}=49\times 25\]
According to question,
\[{{S}_{x-1}}={{S}_{49}}-{{S}_{x}}\]
\[\Rightarrow \dfrac{{{x}^{2}}-x}{2}=49\times 25-\dfrac{{{x}^{2}}+x}{2}\]
\[\Rightarrow \dfrac{{{x}^{2}}-x}{2}+\dfrac{{{x}^{2}}+x}{2}=49\times 25\]
\[\Rightarrow {{x}^{2}}=49\times 25\]
\[\Rightarrow x=\pm 35\]
Since, \[x\] is a counting number, so negative value will be neglected.
\[\therefore x=35\]
12. Find the first term and the common difference \[\dfrac{1}{3},\dfrac{5}{3},\dfrac{9}{3}\] .
Ans: Given AP: \[\dfrac{1}{3},\dfrac{5}{3},\dfrac{9}{3}\]
First term: \[a=\dfrac{1}{3}\]
Common difference: \[d=\dfrac{5}{3}-\dfrac{1}{3}=\dfrac{4}{3}\]
13. Does \[\sqrt{3},\sqrt{6},\sqrt{9},....\] form an AP?
Ans: Here, \[{{a}_{1}}=\sqrt{3},{{a}_{2}}=\sqrt{6},{{a}_{3}}=\sqrt{9}\]
\[{{d}_{1}}=\sqrt{6}-\sqrt{3}\]
\[\Rightarrow {{d}_{1}}=\sqrt{3}(\sqrt{2}-1)\]
\[{{d}_{2}}=\sqrt{9}-\sqrt{6}\]
\[\Rightarrow {{d}_{2}}=3-\sqrt{6}\]
Since \[{{d}_{1}}\ne {{d}_{2}}\] ,
Hence, it is not an AP.
14. Which is the next term of the AP \[\sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},....\]
Ans: Given AP is \[\sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},....\]
Here, \[d=\sqrt{8}-\sqrt{2}\]
\[\Rightarrow d=\sqrt{2}\]
\[{{a}_{5}}=a+(5-1)d\]
\[\therefore {{a}_{5}}=5\sqrt{2}\]
Next term is \[5\sqrt{2}\] or \[\sqrt{50}\]
15. Find the \[{{11}^{th}}\] term from the last term of the AP. \[10,7,4,...,-62\].
Ans: Here, we consider the AP in reverse
\[\therefore a=-62,d=-(7-10)=3\]
\[{{a}_{11}}=a+10d\]
\[\therefore {{a}_{11}}=-32\]
Therefore, \[{{11}^{th}}\] term from the last is \[-32\] .
16. If \[x+1,3x\] and \[4x+2\] are in A.P, find the value of \[x\] .
Ans: Since \[x+1,3x\] and \[4x+2\] are in AP
\[2(3x)=x+1+4x+2\]
\[\therefore x=3\]
17. Find the sum of first \[n\] odd natural numbers.
Ans: AP of odd numbers are \[1,3,5,7,.....\]
\[a=1,d=3-1=2\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{n}}=\dfrac{n}{2}\left[ 2\times 1+(n-1)2 \right]\]
\[\therefore {{S}_{n}}={{n}^{2}}\]
18. Find the \[{{12}^{th}}\] term of the AP \[\sqrt{2},3\sqrt{2},5\sqrt{2}....\]
Ans: Here, \[a=\sqrt{2},d=3\sqrt{2}-\sqrt{2}=2\sqrt{2}\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[{{a}_{12}}=a+11d\]
\[\Rightarrow {{a}_{12}}=\sqrt{2}+11\left( 2\sqrt{2} \right)\]
\[\therefore {{a}_{12}}=23\sqrt{2}\]
19. Find the sum of first \[11\] terms of AP \[2,6,10,...\]
Ans: Here, \[a=2,d=6-2=4\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{11}}=\dfrac{11}{2}\left[ 2\times 2+(11-1)\times 4 \right]\]
\[\therefore {{S}_{11}}=242\]
20.Find the sum of the first hundred even natural numbers divisible by \[5\].
Ans: Even natural no. divisible by \[5\] are \[10,20,30,...\]
Here, \[a=10,d=10,n=100\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{100}}=\dfrac{100}{2}\left[ 2\left( 10 \right)+10\left( 100-1 \right) \right]\]
\[\therefore {{S}_{100}}=50500\]
21. Find \[{{a}_{30}}-{{a}_{20}}\] for the A.P \[-9,-14,-19,-24,...\]
Ans: Here, \[a=-9\]
\[d=-14+9\]
\[\Rightarrow d=-5\]
\[\Rightarrow {{a}_{30}}-{{a}_{20}}=a+29d-a-19d\]
\[\Rightarrow {{a}_{30}}-{{a}_{20}}=10d\]
\[\therefore {{a}_{30}}-{{a}_{20}}=-50\]
22. Find the common difference and write the next two terms of the AP \[{{1}^{2}},{{5}^{2}},{{7}^{2}},73,...\]
Ans: Given AP \[{{1}^{2}},{{5}^{2}},{{7}^{2}},73,...\]
\[\Rightarrow 1,25,49,73,...\]
\[d={{a}_{2}}-{{a}_{1}}\]
\[\Rightarrow {{a}_{2}}-{{a}_{1}}=25-1\]
\[\Rightarrow {{a}_{2}}-{{a}_{1}}=24\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Next two terms are,
\[{{a}_{5}}=97\]
\[{{a}_{6}}=121\]
23. Show that sequence defined by \[{{a}_{n}}=3+2n\] is an AP.
Ans: Here, \[{{a}_{1}}=5,{{a}_{2}}=7,{{a}_{3}}=9,{{a}_{4}}=11\]
Common difference:
\[d=7-5\]
\[d=11-9\]
\[\therefore d=2\]
Hence, it is AP.
24. The first term of an AP is \[-7\] and common difference \[5\] . Find its general term.
Ans: Here, \[a=-7,d=5\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[{{a}_{n}}=-7+5\left( n-1 \right)\]
\[{{a}_{n}}=5n-12\]
25. How many terms are there in A.P? \[18,15\dfrac{1}{2},13,....,-47\]
Ans: Here, \[a=18,d=\dfrac{31}{2}-\dfrac{18}{1}=\dfrac{-5}{2}\]
\[{{a}_{n}}=-47\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow -47=18+\left( n-1 \right)\left( \dfrac{-5}{2} \right)\]
\[\therefore n=27\]
26. In an AP, the sum of first \[n\] terms is \[\dfrac{3{{n}^{2}}}{2}+\dfrac{13}{2}n\] find its \[{{2}^{nd}}\] term.
Ans: Given \[{{S}_{n}}=\dfrac{3{{n}^{2}}}{2}+\dfrac{13}{2}n\]
Put \[n=1,2,3,...\]
\[{{S}_{1}}=\dfrac{16}{2}=8\]
\[{{S}_{2}}=19\]
\[{{a}_{1}}={{S}_{1}}=8\]
\[{{a}_{2}}={{S}_{2}}-{{S}_{1}}\]
\[\therefore {{a}_{2}}=11\]
27. Show that the progression \[4,7\dfrac{1}{2},10\dfrac{1}{2},13\dfrac{3}{4},17,..\] is an AP.
Ans: Common difference: \[{{d}_{1}}=\dfrac{29}{4}-\dfrac{4}{1}\]
\[\Rightarrow {{d}_{1}}=\dfrac{13}{4}\]
Also,
\[{{d}_{2}}=\dfrac{21}{2}-\dfrac{29}{4}\]
\[\Rightarrow {{d}_{2}}=\dfrac{13}{4}\]
\[\because {{d}_{1}}={{d}_{2}}\]
Hence, it is an AP.
Short Answer Questions (3 Marks)
1. Write first four terms of the AP, when the first term \[a\] and common difference \[d\] are given as follows:
(i) \[a=10,d=10\]
Ans: (i) Given: \[a=10,d=10\]
Using these values we get,
First term: \[a=10\]
Second term: \[a+d=20\]
Third term: \[a+2d=30\]
Fourth term: \[a+3d=40\]
Therefore, first four terms are: \[10,20,30,40\]
(ii) \[a=-2,d=0\]
Ans: (ii) Given: \[a=-2,d=0\]
Using these values we get,
First term: \[a=-2\]
Second term: \[a+d=-2\]
Third term: \[a+2d=-2\]
Fourth term: \[a+3d=-2\]
Therefore, first four terms are: \[-2,-2,-2,-2\]
(iii) \[a=4,d=-3\]
Ans: (iii) Given: \[a=4,d=-3\]
Using these values we get,
First term: \[a=4\]
Second term: \[a+d=1\]
Third term: \[a+2d=-2\]
Fourth term: \[a+3d=-5\]
Therefore, first four terms are: \[4,1,-2,-5\]
(iv) \[a=-1,d=\dfrac{1}{2}\]
Ans: (iv) Given: \[a=-1,d=\dfrac{1}{2}\]
Using these values we get,
First term: \[a=-1\]
Second term: \[a+d=\dfrac{-1}{2}\]
Third term: \[a+2d=0\]
Fourth term: \[a+3d=\dfrac{1}{2}\]
Therefore, first four terms are: \[-1,\dfrac{-1}{2},0,\dfrac{1}{2}\]
(v) \[a=-1.25,d=-0.25\]
Ans: (v) Given: \[a=-1.25,d=-0.25\]
Using these values we get,
First term: \[a=-1.25\]
Second term: \[a+d=-1.50\]
Third term: \[a+2d=-1.75\]
Fourth term: \[a+3d=-2.00\]
Therefore, first four terms are: \[-1.25,-1.50,-1.75,-2.00\]
2. Find the \[{{31}^{st}}\] term of an AP whose \[{{11}^{th}}\] term is \[38\] and \[{{16}^{th}}\] term is \[73\] .
Ans: Given that: \[{{a}_{11}}=38\] and \[{{a}_{16}}=73\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[\Rightarrow 38=a+\left( 11-1 \right)d\]
\[\therefore ~38=a+10d\] …(1)
Also,
\[\Rightarrow ~73=a+\left( 16-1 \right)d\]
\[\therefore ~73=a+15d\] …(2)
Solving equation (1) and (2) we get,
Common difference: \[d=7\]
And first term: \[a=-32\]
Again by using formula \[{{a}_{n}}=a+\left( n-1 \right)d\]
We get,
\[{{a}_{31}}=-32+7\left( 31-1 \right)\]
\[\therefore {{a}_{31}}=178\]
Therefore, \[{{31}^{st}}\] term of AP is \[178\] .
3. If the third and the ninth terms of an AP are \[4\] and \[-8\] respectively, which term of this AP is zero?
Ans: Given that: \[{{a}_{3}}=4\] and \[{{a}_{9}}=-8\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
Putting the given values,
\[\Rightarrow 4=a+\left( 3-1 \right)d\]
\[\therefore ~4=a+2d\] …(1)
Also,
\[\Rightarrow ~-8=a+\left( 9-1 \right)d\]
\[\therefore ~-8=a+8d\] …(2)
Solving equation (1) and (2) we get,
Common difference: \[d=-2\]
And first term: \[a=8\]
Again by using formula \[{{a}_{n}}=a+\left( n-1 \right)d\]
We get,
\[0=8-2\left( n-1 \right)\]
\[\therefore n=5\]
Therefore, \[{{5}^{th}}\] term of AP is \[0\] .
4. Two AP's have the same common difference. The difference between their \[{{100}^{th}}\] terms is \[100\] , what is the difference between their \[{{1000}^{th}}\] terms.
Ans: Let first term of \[{{1}^{st}}\] AP be \[a\]
Let first term of \[{{2}^{nd}}\] AP be \[a'\]
It is given that their common difference is same.
Let their common difference be \[d\]
It is given that difference between their terms \[{{100}^{th}}\] is \[100\] .
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[a+\left( 100-1 \right)d\text{ }\left[ a\prime +\left( 100-1 \right)d \right]\]
\[\Rightarrow a+99d-a\prime -99d=100\]
\[\therefore a-a\prime =100\] …(1)
We have to find difference between their \[{{1000}^{th}}\] terms,
\[\therefore a+\left( 1000-1 \right)d\text{ }\left[ a\prime +\left( 1000-1 \right)d \right]\]
\[\Rightarrow a+999d-a\prime -999d\]
\[\Rightarrow aa\prime ~\]
Putting equation (1) in the above equation we get,
\[aa\prime ~=100\]
Therefore, difference between their \[{{1000}^{th}}\] terms would be equal to \[100\] .
5. How many three-digit numbers are divisible by \[7\] ?
Ans: From the given data we have the AP:
\[105,112,119,...,994\]
Let \[994\] be the \[{{n}^{th}}\] term of the AP.
We need to find \[n\] here.
Here, First term: \[a=105\], Common difference: \[d=7\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 994=105+\left( n-1 \right)\left( 7 \right)\]
\[\therefore n=128\]
Therefore, there are \[128\] terms in the given AP.
6. A contract on a construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. \[200\] for the first day, Rs \[250\] for the second day, Rs \[300\] for the third day, etc., the penalty for each succeeding day being Rs \[50\] more than for the preceding day. How much money the contractor has to pay a penalty if he has delayed the work by \[30\] days?
Ans: Given that:
Penalty for first day is Rs \[200\] ,
Penalty for second day is Rs \[250\] ,
Penalty for third day is Rs \[300\] .
We want to know how much money the contractor has to pay as penalty, if he has delayed the work by \[30\] days.
So, we have an AP of the form \[200,250,300,350,....30terms\]
Here,
First term: \[a=200\] , Common difference: \[d=50\] , number of terms: \[n=30\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{30}}=\dfrac{30}{2}\left[ 400+\left( 30-1 \right)50 \right]\]
\[\therefore {{S}_{30}}=27750\]
Therefore, penalty for \[30\] days is Rs. \[27750\] .
7. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g, a section of Class I will plant one tree, a section of class II will plant two trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
Ans: Given that:
The number of trees planted by class I = number of sections × 1 = 3 × 1 = 3
The number of trees planted by class II = number of sections × 2 = 3 × 2 = 6
The number of trees planted by class III = number of sections × 3 = 3 × 3 = 9
Therefore, we have sequence of the form \[3,6,9,...,12terms\]
To find total number of trees planted by all the students, we need to find sum of this sequence.
Here, First term: \[a=3\] ,
Common difference: \[d=3\] and
Number of terms: \[n=12\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{12}}=\dfrac{12}{2}\left[ 6+3\left( 12-1 \right) \right]\]
\[\therefore {{S}_{12}}=234\]
Total \[234\] trees will be planted by the students.
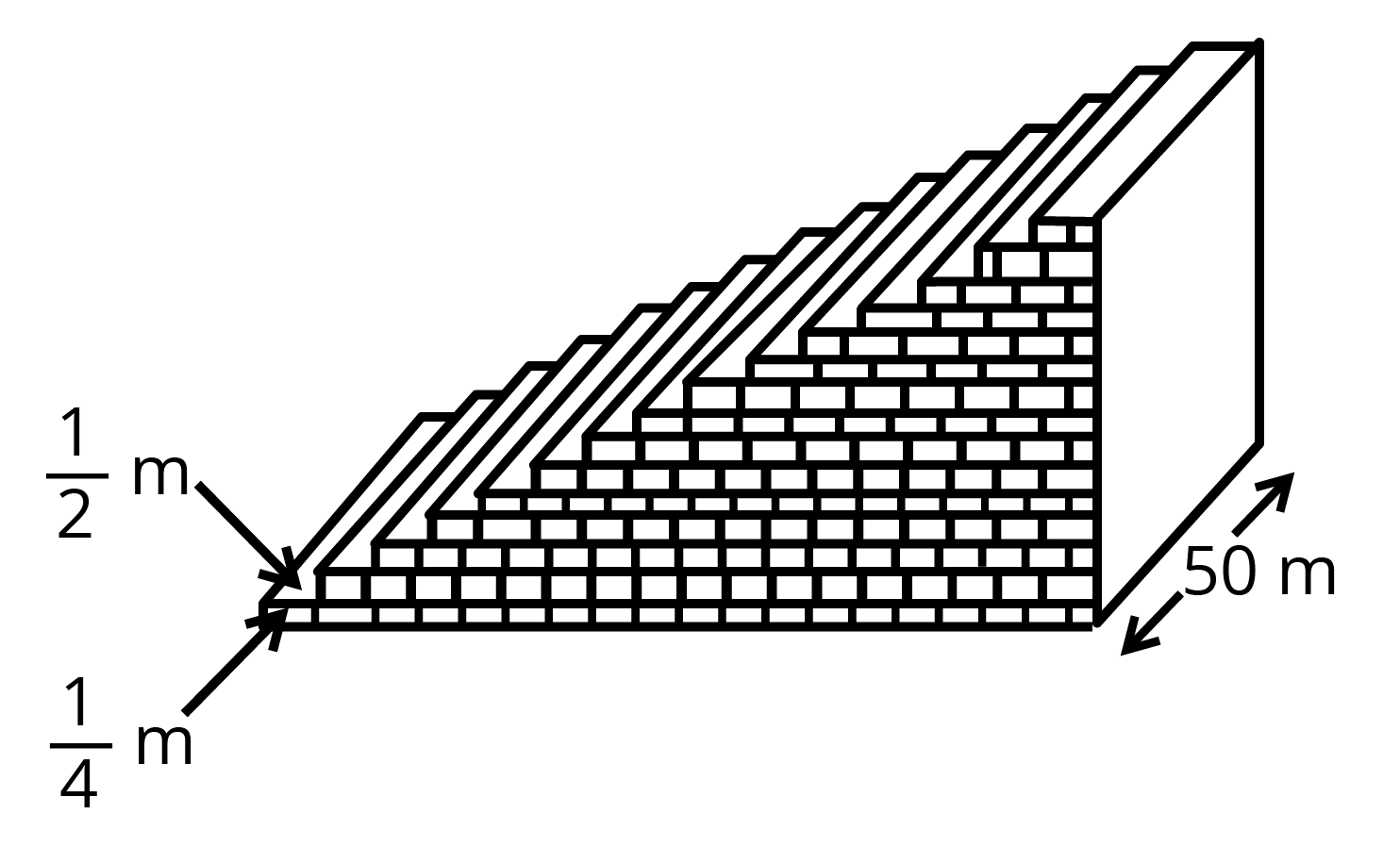
8. A small terrace at a football ground comprises of \[15\] steps each of which is \[50\] m long and built of solid concrete. Each step has a rise of \[\dfrac{1}{4}\] m and a tread of \[\dfrac{1}{2}\] m (see figure). Calculate the total volume of concrete required to build the terrace.
Ans: Volume of concrete required to build the first step, second step, third step,… are:
\[\dfrac{1}{4}\times \dfrac{1}{2}\times 50,\left( 2\times \dfrac{1}{4} \right)\times \dfrac{1}{2}\times 50,\left( 3\times \dfrac{1}{4} \right)\times \dfrac{1}{2}\times 50,...\]
\[\Rightarrow \dfrac{50}{8},2\times \dfrac{50}{8},3\times \dfrac{50}{8},...\]
To find the total volume of concrete required,
Use the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{15}}=\dfrac{50}{8}\left( \dfrac{15}{2}\left[ 2+\left( 15-1 \right) \right] \right)\]
\[\therefore {{S}_{15}}=750\]
The total volume of concrete required to build the terrace is \[750{{m}^{3}}\].
9. For what value of n are the \[{{n}^{th}}\] term of the following two AP’s are same \[13,19,25,...\] and \[69,68,67,...\] .
Ans: Given that: \[{{n}^{th}}\] term of \[13,19,25,...\] is equal to \[{{n}^{th}}\] term of \[69,68,67,...\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 7\left( n-1 \right)=56\]
\[\therefore n=9\]
10. Check whether \[301\] is a term of the list of numbers \[5,11,17,32,...\] ?
Ans: Given AP is \[5,11,17,32,...\]
Here, \[a=5,d=6\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 301=5+6\left( n-1 \right)\]
\[\therefore n=\dfrac{302}{6}\]
Since \[n\] cannot be a fraction.
Therefore, \[301\] is not a term of the given AP.
11. Determine the AP whose third term is \[16\] and the \[{{7}^{th}}\] term exceeds the \[{{5}^{th}}\] term by \[12\] .
Ans: Given \[{{a}_{3}}=16\] and \[{{a}_{7}}={{a}_{5}}+12\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow a+2d=16\] …(1)
And \[\Rightarrow a+6d=a+4d+12\]
\[\therefore d=6\]
Put the value of \[d\] in equation (1),
\[a+2\times 6=16\]
\[\therefore a=4\]
Therefore, the AP is \[4,10,16,...\]
12. Find the sum of AP in \[-5+(-8)+(-11)+....+(-230)\] .
Ans: Here, \[a=-5,d=-3,{{a}_{n}}=-230\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow -230=-5-3\left( n-1 \right)\]
\[\therefore n=76\]
Use the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{76}}=\dfrac{76}{2}\left[ -10-3\left( 76-1 \right) \right]\]
\[\therefore {{S}_{76}}=-8930\]
13. In an AP, \[{{a}_{n}}=4,d=2,{{S}_{n}}=-14\] find \[n\] and \[a\] .
Ans: Given that \[{{a}_{n}}=4,d=2,{{S}_{n}}=-14\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 4=a+2\left( n-1 \right)\] …(1)
Use the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow -14=\dfrac{n}{2}\left[ a+4 \right]\] …(2)
From equation (1) and (2) we get,
\[\Rightarrow -28=n\left[ 6-2n+4 \right]\]
\[\Rightarrow {{n}^{2}}-5n-14=0\]
\[\Rightarrow n=7,-2\]
\[\therefore a=-8\]
14. Find \[{{a}_{30}}-{{a}_{20}}\] for the AP in \[-9,-14,-19,-24,...\]
Ans: Here, \[a=-9\] and \[d=-5\]
\[{{a}_{30}}-{{a}_{20}}=(a+29d)-(a+19d)\]
\[\therefore {{a}_{30}}-{{a}_{20}}=-50\]
15. Find the sum to \[n\] terms of the AP in \[5,2,-1,-4,-7,...\]
Ans: Here, \[a=5\] and \[d=-3\]
Use the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2\times 5+(n-1)(-3) \right]\]
\[{{S}_{n}}=\dfrac{n}{2}\left[ 13-3n \right]\]
16. Find the sum of first \[24\] terms of the list of no. whose \[{{n}^{th}}\] term is given by \[{{a}_{n}}=3+2n\] .
Ans: Given that: \[{{a}_{n}}=3+2n\]
Put \[n=1,2,3,...\]
\[{{a}_{1}}=5,{{a}_{2}}=7,{{a}_{3}}=9...\]
Here, \[a=5,d=2\]
Use the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{24}}=\dfrac{24}{2}\left[ 2\times 5+(24-1)\times 2 \right]\]
\[\therefore {{S}_{24}}=672\]
Long Answer Questions (4 Marks)
1. For the following APs, write the first term and the common difference.
(i). \[3,1,-1,-3,...\]
Ans: (i) Given AP is \[3,1,-1,-3,...\]
First term: \[a=3\]
Common difference:
\[d=1-3\]
\[\therefore d=-2\]
(ii). \[-5,-1,3,7,...\]
Ans: (ii) Given AP is \[-5,-1,3,7,...\]
First term: \[a=-5\]
Common difference:
\[d=-1-\left( -5 \right)\]
\[\therefore d=4\]
(iii). \[\dfrac{1}{3},\dfrac{5}{3},\dfrac{9}{3},\dfrac{13}{3}...\]
Ans: (iii) Given AP is \[\dfrac{1}{3},\dfrac{5}{3},\dfrac{9}{3},\dfrac{13}{3}...\]
First term: \[a=\dfrac{1}{3}\]
Common difference:
\[d=\dfrac{5}{3}-\dfrac{1}{3}\]
\[\therefore d=\dfrac{4}{3}\]
(iv). \[0.6,1.7,2.8,3.9,...\]
Ans: (iv) Given AP is \[0.6,1.7,2.8,3.9,...\]
First term: \[a=0.6\]
Common difference:
\[d=1.7-0.6\]
\[\therefore d=1.1\]
2. The \[{{17}^{th}}\] term of an AP exceeds its \[{{10}^{th}}\] term by \[7\] . Find the common difference.
Ans: Given that: \[{{a}_{17}}={{a}_{10}}+7\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[a+16d=a+9d+7\]
\[\Rightarrow 7d=7\]
\[\therefore d=7\]
Common difference of the given AP is \[7\] .
3. A sum of Rs \[700\] is to be used to give seven cash prizes to students of a school for their overall academic performance. If, each prize is Rs \[20\] less than its preceding term, find the value of each of the prizes.
Ans: It is given that sum of seven cash prizes is equal to Rs \[700\] .
And, each prize is Rs \[20\] less than its preceding term.
Let the value of first prize be Rs \[a\]
Let value of second prize be Rs \[\left( a-20 \right)\]
Let value of third prize be Rs \[\left( a-40 \right)\]
So, we have sequence of the form:
\[a,a-20,a-40,a-60,...\]
It is an arithmetic progression because the difference between consecutive terms is constant.
Here, first term is \[a\] ,
Common difference: \[d=-20\]
\[n=7\] (Because there are total of seven prizes)
\[{{S}_{7}}=Rs700\] (given)
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{7}}=\dfrac{7}{2}\left[ 2\times a+(7-1)\times -20 \right]\]
\[\Rightarrow 200=2a-120\]
\[\therefore a=160\]
Therefore, the value of prizes is \[160,140,120,100,80,60,40\] respectively.
4. A spiral is made up of successive semicircles, with centers alternatively at \[A\] and \[B\], starting with center at \[A\], of radii \[0.5\] cm, \[1.0\] cm, \[1.5\] cm, \[2.0\] cm, ... What is the total length of such a spiral made up of thirteen consecutive semicircles.
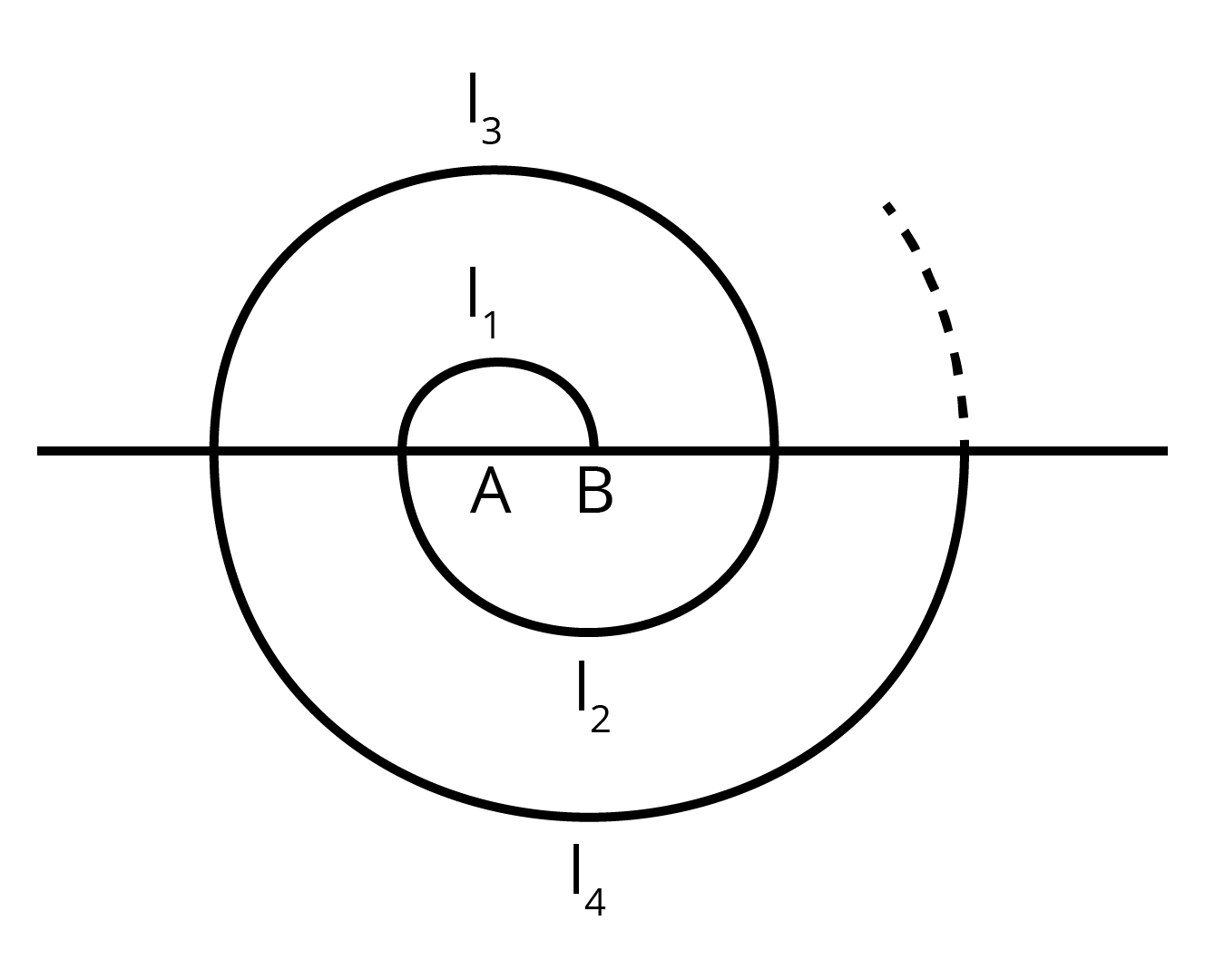
Ans: The Length of semi–circle is $ \dfrac{\text{Circumferenceofcircle}}{2}=\dfrac{2\pi r}{2}=\pi r $
The Length of semicircle of radii \[0.5\] cm is \[0.5\pi \] cm
The Length of semicircle of radii \[1.0\] cm is \[\pi \] cm
The Length of semicircle of radii \[1.5\] cm is \[1.5\pi \] cm
Therefore, we have sequence of the form:
\[0.5\pi ,1.0\pi ,1.5\pi ,....13terms\]
To find total length of the spiral, we need to find sum of the sequence.
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
Here, \[a=0.5,d=0.5,n=13\]
\[\Rightarrow {{S}_{13}}=\dfrac{13}{2}\left[ 1+0.5\left( 13-1 \right) \right]\]
\[\therefore {{S}_{13}}=45.5\]
Total length of spiral is \[45.5\pi =143cm\] .
5. \[200\] logs are stacked in the following manner: \[20\] logs in the bottom row, \[19\] in the next row, \[18\] in the row next to it, and so on. In how many rows are the \[200\] logs placed and how many logs are in the top row?
Ans: Given that:
The number of logs in the bottom row is \[20\]
The number of logs in the next row is \[19\]
The number of logs in the next to next row is \[18\]
Therefore, we have a sequence of the form \[20,19,18,...\]
Here, \[a=20,d=-1\]
We need to find that how many rows make total of 200 logs.
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
Putting the given values we get,
\[\Rightarrow 200=\dfrac{n}{2}\left( 40-n+1 \right)\]
\[\Rightarrow {{n}^{2}}-41n+400=0\]
\[\therefore n=25,16\]
We can discard \[n=25\] because we cannot have more than \[20\] rows in the sequence. \[\therefore n=16\] which means \[16\] rows make total number of logs equal to \[200\] .
We also need to find number of logs in the top row.
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[{{a}_{16}}=20-15\]
\[\therefore {{a}_{16}}=5\]
Therefore, there are \[5\] logs in the topmost row and there is a total of \[16\] rows.
6. In a potato race, a bucket is placed at the starting point, which is \[5\] meters from the first potato, and the other potatoes are placed \[3\] meters apart in a straight line. There are ten potatoes in the line. A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
Ans: Given that:
The distance of the first potato from the starting point is \[5\] meters
Therefore, the distance covered by the competitor to pick up the first potato and put it in the bucket is \[5\times 2=10m\]
The distance of the Second potato from the starting point is \[5+3=8\] meters
Therefore, the distance covered by the competitor to pick up the second potato and put it in the bucket is \[8\times 2=16\] meters
The distance of the third potato from the starting point is \[8+3=11\] meters
Therefore, the distance covered by the competitor to pick up third potato and put it in the bucket is \[11\times 2=22\] meters
Therefore, we have a sequence of the form \[10,16,22,...10terms\]
(There are ten terms because there are ten potatoes)
The total distance covered by the competitor is:
Here, \[a=10,d=6,n=10\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
Putting the given values we get,
\[{{S}_{10}}=\dfrac{10}{2}\left[ 20+6\left( 10-1 \right) \right]\]
\[\therefore {{S}_{10}}=370\]
7. Which term of the sequence \[20,19\dfrac{1}{4},18\dfrac{1}{2},17\dfrac{3}{4},...\] is the first negative term?
Ans: For first negative term, \[{{a}_{n}}<0\]
Here, \[a=20,d=\dfrac{-3}{4}\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow \dfrac{20}{1}-\dfrac{3}{4}n+\dfrac{3}{4}<0\]
\[\Rightarrow \dfrac{80-3n+3}{4}<0\]
\[\Rightarrow n>\dfrac{83}{3}\]
Therefore, \[{{28}^{th}}\] term is the first negative term.
8. The \[{{p}^{th}}\] term of an AP is \[q\] and \[{{q}^{th}}\] term is \[p\]. Find its \[{{(p+q)}^{th}}\] term.
Ans: Given that
\[{{a}_{p}}=q\]
\[\Rightarrow a+\left( p-1 \right)d=q\] …(1)
\[{{a}_{q}}=p\]
\[\Rightarrow a+\left( q-1 \right)d=p\] …(2)
From equations (1) and (2),
\[\Rightarrow d\left[ pq \right]=qp\text{ }\]
\[\therefore d=-1\]
Putting it in equation (1) we get,
\[a=q+p-1~\]
We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\Rightarrow {{a}_{p+q}}=\left( q+p1 \right)-1\left( p+q1 \right)\]
\[\therefore {{a}_{p+q}}=0\]
9. If \[m\] times the \[{{m}^{th}}\] term of an A.P is equal to \[n\] times its \[{{n}^{th}}\] term, show that the \[{{(m+n)}^{th}}\] term of the AP is zero.
Ans: Given that: \[{{(m+n)}^{th}}\]
We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\therefore m[a+(m-1)d]=n[a+(n-1)d]\]
\[\Rightarrow ma+{{m}^{2}}d-md=na+{{n}^{2}}d-nd\]
\[\Rightarrow a(m-n)+({{m}^{2}}-{{n}^{2}})d-md+nd=0\]
\[\Rightarrow a(m-n)+(m-n)(m+n)d-(m-n)d=0\]
\[\Rightarrow (m-n)[a+(m+n-1)d]=0\]
\[\Rightarrow a+(m+n-1)d=0\]
\[\therefore {{a}_{m+n}}=0\]
Hence Proved.
10. The sum of the \[{{4}^{th}}\] and \[{{8}^{th}}\] terms of an AP is \[24\] and the sum of the \[{{6}^{th}}\] and \[{{10}^{th}}\] terms is \[44\] . Find the first three terms of the AP.
Ans: We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[{{a}_{4}}+{{a}_{8}}=24\] (Given)
\[\therefore a+3d+a+7d=24\]
\[\Rightarrow a+5d=12\] …(1)
Also, \[{{a}_{5}}+{{a}_{10}}=44\] (Given)
\[\Rightarrow a+5d+a+9d=44\]
\[\Rightarrow a+7d=22\] …(2)
On solving equations (1) and (2),
\[d=5,a=-13\]
Therefore, First three terms are \[-13,-8,-3\]
11. If the sum of \[n\] terms of an AP is \[3{{n}^{2}}+5n\] and its \[{{m}^{th}}\] term is \[164\], find the value of \[m\] .
Ans: Given that: \[{{S}_{n}}=3{{n}^{2}}+5n\]
Put \[n=1,2,3,...\] ,
\[\therefore {{S}_{1}}=8\] and
\[{{S}_{2}}=22\]
\[\therefore {{a}_{1}}={{S}_{1}}=8\] and
\[{{a}_{2}}={{S}_{2}}-{{S}_{1}}\]
\[\therefore {{a}_{2}}=14\]
\[d=6\]
\[{{a}_{m}}=164\] (Given)
\[\therefore 8+(m-1)(6)=164\]
\[\therefore m=27\]
12. If the sum of three numbers in AP, be \[24\] and their product is \[440\] , find the numbers.
Ans: Let numbers be \[a-d,a,a+d\]
\[(a-d)+a+(a+d)=24\] (Given)
\[\therefore a=8\]
\[(a-d)(a)(a+d)=440\]
\[\Rightarrow (8-d).8.(8-d)=440\]
\[\Rightarrow {{8}^{2}}-{{d}^{2}}=55\]
\[\therefore d=\pm 3\]
If \[d=3\]
Then AP is \[5,8,11,...\]
If \[d=-3\]
Then AP is \[11,8,5,...\]
13. If \[{{a}^{2}},{{b}^{2}},{{c}^{2}}\] are in AP, then prove that \[\dfrac{1}{b+c},\dfrac{1}{c+a},\dfrac{1}{a+b}\] are in AP.
Ans: Given \[{{a}^{2}},{{b}^{2}},{{c}^{2}}\] are in AP
Then \[2{{b}^{2}}={{a}^{2}}+{{c}^{2}}\] …(1)
If \[\dfrac{1}{b+c},\dfrac{1}{c+a},\dfrac{1}{a+b}\] are in AP then
\[\dfrac{1}{c+a}-\dfrac{1}{b+c}=\dfrac{1}{a+b}-\dfrac{1}{c+a}\]
\[\Rightarrow \dfrac{(b+c)-(c+a)}{(c+a)(b+c)}=\dfrac{(c+a)-(a+b)}{(a+b)(c+a)}\]
\[\Rightarrow \dfrac{b-a}{b+c}=\dfrac{c-b}{a+b}\]
\[\therefore 2{{b}^{2}}={{c}^{2}}+{{a}^{2}}\] …(2)
From (1) and (2),
Hence proved.
14. If \[{{S}_{1}},{{S}_{2}},{{S}_{3}}\] be the sum of \[n,2n,3n\] terms respectively of an AP, prove that \[{{S}_{3}}=3({{S}_{2}}-{{S}_{1}})\] .
Ans: We know that,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\therefore {{S}_{1}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[{{S}_{2}}=\dfrac{2n}{2}\left[ 2a+\left( 2n-1 \right)d \right]\]
\[{{S}_{3}}=\dfrac{3n}{2}\left[ 2a+\left( 3n-1 \right)d \right]\]
We have to prove that \[{{S}_{3}}=3({{S}_{2}}-{{S}_{1}})\]
RHS: \[\Rightarrow 3\left( \dfrac{2n}{2}\left[ 2a+\left( 2n-1 \right)d \right]-\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right] \right)\]
\[\Rightarrow 3\left( \dfrac{n}{2}\left[ 2a+3nd-d \right] \right)\]
\[\Rightarrow {{S}_{3}}\]
Here, \[LHS=RHS\]
Hence proved.
15. The ratio of the sums of \[m\] and \[n\] terms of an AP is \[{{m}^{2}}:{{n}^{2}}\] , show that the ratio of the \[{{m}^{th}}\] and \[{{n}^{th}}\] term is \[(2m-1):(2n-1)\]
Ans: We know that,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
Therefore,
\[\dfrac{{{S}_{m}}}{{{S}_{n}}}=\dfrac{\dfrac{m}{2}[2a+(m-a)d]}{\dfrac{n}{2}[2a+(n-1)d]}\]
\[\Rightarrow \dfrac{{{m}^{2}}}{{{n}^{2}}}=\dfrac{m}{n}\left[ \dfrac{2a+(m-1)d}{2a+(n-1)d} \right]\] (Given)
\[\Rightarrow \dfrac{m}{n}=\left[ \dfrac{2a+(m-1)d}{2a+(n-1)d} \right]\]
\[\Rightarrow 2am+mnd-md=2an+mnd-nd\]
\[\Rightarrow 2am-2an-md+nd=0\]
\[\Rightarrow (m-n)(2a-d)=0\]
\[\Rightarrow 2a=d\] …(1)
According to question,
\[\Rightarrow \dfrac{{{a}_{m}}}{{{a}_{n}}}=\dfrac{a+(m-1)d}{a+(n-1)d}\]
From equation (1),
\[\Rightarrow \dfrac{{{a}_{m}}}{{{a}_{n}}}=\dfrac{a+(m-1)2a}{a+(n+1)2a}\]
\[\Rightarrow \dfrac{{{a}_{m}}}{{{a}_{n}}}=\dfrac{2m-1}{2n-1}\]
Hence proved.
16. If the sum of first \[p\] terms of an AP is the same as the sum of its first \[q\] terms, show that the sum of the first \[(p+q)\] terms is zero.
Ans: Given that: \[{{S}_{P}}={{S}_{q}}\]
We know that,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\therefore \dfrac{p}{2}[2a+(p-1)d]=\dfrac{q}{2}[2a+(q-1)d]\]
\[\Rightarrow 2ap+{{p}^{2}}d-pd=2aq+{{q}^{2}}d-qd\]
\[\Rightarrow 2a(p-q)+(p-q)(p-q)d-(p-q)d=0\]
\[\Rightarrow (p-q)[2a+(p+q-1)d]=0\]
\[\therefore {{S}_{p+q}}=0\]
Hence Proved.
17. For the A.P \[{{a}_{1}},{{a}_{2}},{{a}_{3}},...\] If \[\dfrac{{{a}_{4}}}{{{a}_{7}}}=\dfrac{2}{3}\] find \[\dfrac{{{a}_{6}}}{{{a}_{8}}}\] .
Ans: Given that \[\dfrac{{{a}_{4}}}{{{a}_{7}}}=\dfrac{2}{3}\]
We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\therefore \dfrac{a+3d}{a+6d}=\dfrac{2}{3}\]
\[\Rightarrow 3a+9d=2a+12d\]
\[\Rightarrow a=3d\]
\[\therefore \dfrac{{{a}_{6}}}{{{a}_{7}}}=\dfrac{a+5d}{a+6d}\]
\[\Rightarrow \dfrac{{{a}_{6}}}{{{a}_{7}}}=\dfrac{3d+5d}{3d+6d}\]
\[\Rightarrow \dfrac{{{a}_{6}}}{{{a}_{7}}}=\dfrac{8}{9}\]
18. In an AP \[{{p}^{th}}\], \[{{q}^{th}}\] and \[{{r}^{th}}\] terms are respectively \[a,b,c\] . Prove that \[p(b-c)+q(c-a)+r(a-b)=0\] .
Ans: We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
Therefore,
\[A+(p-1)D=a\] …(1)
\[A+(q-1)D=b\] …(2)
\[A+(r-1)D=c\] …(3)
Equation (2) – (3),
\[\Rightarrow b-c=(q-1)D-(r-1)D\]
\[\Rightarrow b-c=D(q-r)\]
\[\Rightarrow p(b-c)=pD(q-r)\] …(4)
Similarly,
\[q(c-a)=qD(r-p)\] …(5)
\[r(a-b)=rD(p-q)\] …(6)
Adding (4), (5) and (6) we get,
\[\Rightarrow p(b-c)+q(c-a)+r(a-b)=0\]
Hence proved.
19. If \[{{(p+1)}^{th}}\] term of an A.P is twice the \[{{(q+1)}^{th}}\] term, show that \[{{(3p+1)}^{th}}\] term is twice the \[{{(p+q+1)}^{th}}\] term.
Ans: Given that: $ {{a}_{p+1}}=2{{a}_{q+1}} $
We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\therefore a+(p+1-1)d=2[a+(q+1-1)d]\]
\[\Rightarrow a+pd=2a+2qd\]
\[\Rightarrow (p-2q)d=a\]
Now, \[\dfrac{{{a}_{3p+1}}}{{{a}_{p+q+1}}}=\dfrac{a+(3p+1-1)d}{a+(p+q+1-1)d}\]
\[\Rightarrow \dfrac{(p-2q)d+3pd}{p-2q+(p+q)d}=2\]
Hence proved that \[{{(3p+1)}^{th}}\] term is twice the \[{{(p+q+1)}^{th}}\] term.
20. The sum of four numbers in AP is \[50\] and the greatest number four times the least. Find the numbers.
Ans: Let the numbers be \[(a-3d),(a-d),(a+d),(a+3d)\]
Given that:
\[(a-3d)+(a-d)+(a+d)+(a+3d)=50\]
\[\Rightarrow 4a=50\]
\[\therefore a=12.5\]
According to question,
\[(a+3d)=4\times (a-3d)\]
\[\Rightarrow a=5d\]
\[\therefore d=2.5\]
Numbers are \[5,10,15,20\]
21. Find the sum of all integers between \[84\] and \[719\] which are multiples of \[5\] .
Ans: The numbers are \[85,90,95,....,715\]
Here, \[a=85,d=5,{{a}_{n}}=715\]
We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\Rightarrow 85+5(n-1)=715\]
\[\Rightarrow n=127\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{127}}=\dfrac{127}{2}(85+715)\]
\[\Rightarrow {{S}_{127}}=50800\]
22. If \[{{m}^{th}}\] term of an A.P is \[\dfrac{1}{n}\] and the \[{{n}^{th}}\] term is \[\dfrac{1}{m}\] show that the sum of terms is \[\dfrac{1}{2}(mn+1)\] .
Ans: We know that,
\[{{a}_{n}}=a+\left( n-1 \right)d\]
\[\Rightarrow \dfrac{1}{n}=a+(m-1)d\]
\[\Rightarrow \dfrac{1}{m}=a+(n-1)d\]
On solving the above equations we get,
\[a=\dfrac{1}{mn},d=\dfrac{1}{mn}\]
Using the formula,
\[{{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]\]
\[\Rightarrow {{S}_{mn}}=\dfrac{mn}{2}[2a+(mn-1)d]\]
\[\Rightarrow {{S}_{mn}}=\dfrac{mn}{2}\left[ 2\cdot \dfrac{1}{mn}+(mn-1)\cdot \dfrac{1}{mn} \right]\]
\[\Rightarrow {{S}_{mn}}=\dfrac{1}{2}(mn+1)\]
Hence proved.
23. In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
(i). The taxi fare after each km when the fare is Rs \[15\] for the first km and Rs \[8\] for each additional km.
Ans: (i) Given that Taxi fare for first km is Rs \[15\],
Taxi fare after two km is Rs \[23\] ,
Taxi fare after three km is Rs \[31\]
Taxi fare after four km is Rs \[39\]
Therefore, the sequence is \[15,23,31,39,...\]
It is an arithmetic progression because the difference between any two consecutive terms is equal which is \[8\].
(ii). The amount of air present in a cylinder when a vacuum pump removes \[{{\dfrac{1}{4}}^{th}}\] of the air remaining in the cylinder at a time.
Ans: (ii) Let amount of air initially present in a cylinder be \[V\]
Amount of air left after pumping out air by vacuum pump is \[V-\dfrac{V}{4}=\dfrac{4V-V}{4}=\dfrac{3V}{4}\]
Amount of air left when vacuum pump again pumps out air is \[\dfrac{3}{4}V-\left( \dfrac{1}{4}\times \dfrac{3}{4}V \right)=\dfrac{9}{16}V\]
So, the sequence we get is \[V,\dfrac{3}{4}V,\dfrac{9}{16}V...\]
Checking for difference between consecutive terms,
\[\dfrac{3}{4}V-V=-\dfrac{V}{4}\]
\[\dfrac{9}{16}V-\dfrac{3}{4}V=\dfrac{-3V}{16}\]
The difference between consecutive terms is not equal.
Therefore, it is not an arithmetic progression.
(iii). The cost of digging a well after every meter of digging, when it costs Rs \[150\] for the first meter and rises by Rs \[50\] for each subsequent meter.
Ans. (iii) Cost of digging one meter of well is Rs \[150\]
The cost of digging two meters of well is Rs \[200\]
The cost of digging three meters of well is Rs \[250\]
Therefore, we get a sequence of the form \[150,200,250,...\]
Here, the difference between any two consecutive terms which is also called a common difference is constant and equal to \[50\].
Therefore, it is an AP.
(iv). The amount of money in the account every year, when Rs \[10,000\] is deposited at compound Interest at \[8%\] per annum.
Ans. (iv) Amount in bank after first year is \[10000\left( 1+\dfrac{8}{100} \right)\]
Amount in bank after two years is \[10000{{\left( 1+\dfrac{8}{100} \right)}^{2}}\]
Amount in bank after three years is \[10000{{\left( 1+\dfrac{8}{100} \right)}^{3}}\]
Amount in bank after four years is \[10000{{\left( 1+\dfrac{8}{100} \right)}^{4}}\]
It is not an arithmetic progression because the difference between consecutive terms is not constant.
Therefore, it is not an Arithmetic Progression.
24. In the following AP's find the missing terms:
(i). \[2,\_,26\]
Ans: (i) Given AP: \[2,\_,26\]
We know that difference between consecutive terms is equal in any A.P.
Let the missing term be \[x\] ,
\[\therefore x-2=26-x\]
\[\Rightarrow x=14\]
Therefore, missing term is \[14\] .
(ii). \[\_,13,\_,3\]
Ans: (ii) Given AP: \[\_,13,\_,3\]
Let the missing terms be \[x\] and \[y\] ,
We know that difference between consecutive terms is equal in any A.P.
\[\therefore x-13=3-x\]
\[\Rightarrow x=8\]
And \[13-x=y-13\]
But \[\because x=8\]
\[\therefore y=18\]
Therefore, missing terms are \[8,18\] .
(iii). \[5,\_,\_,9\dfrac{1}{2}\]
Ans: (iii) Given AP: \[5,\_,\_,9\dfrac{1}{2}\]
Here, \[a=5,{{a}_{4}}=9\dfrac{1}{2}\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow \dfrac{19}{2}=5+3d\]
\[\therefore d=\dfrac{3}{2}\]
Second term: \[a+d=5+\dfrac{3}{2}=\dfrac{13}{2}\]
Third term: \[a+2d=\dfrac{13}{2}+\dfrac{3}{2}=8\]
Therefore, missing terms are \[\dfrac{13}{2}\] and \[8\] .
(iv). \[-4,\_,\_,\_,\_,6\]
Ans: (iv) Given AP: \[-4,\_,\_,\_,\_,6\]
Here, \[a=-4,{{a}_{6}}=6\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 6=-4+5d\]
\[\therefore d=2\]
Second term: \[a+d=-4+2=-2\]
Third term: \[a+2d=-4+4=0\]
Fourth term: \[a+3d=-4+6=2\]
Fifth term: \[a+4d=-4+8=4\]
Therefore, missing terms are \[-2,0,2,4\] .
(v). \[\_,38,\_,\_,\_,-22\]
Ans: (v) Given AP: \[\_,38,\_,\_,\_,-22\]
Here, \[{{a}_{2}}=38,{{a}_{6}}=-22\]
Using formula \[{{a}_{n}}=a+\left( n-1 \right)d\] ,
\[\Rightarrow 38=a+d\] and
\[\Rightarrow -22=a+5d\]
Solving the above equations we get,
\[d=-15,a=53\]
First term: \[a=53\]
Third term: \[a+2d=53-30=23\]
Fourth term: \[a+3d=53-45=8\]
Fifth term: \[a+4d=53-60=-7\]
Therefore, missing terms are \[53,23,8,-7\] .
25. The given figure depicts a racing track whose left and right ends are semi-circular. The difference between the two inner parallel line segments is \[60\] m and they are each \[106\] m long. If the track is \[10\] m wide, find:
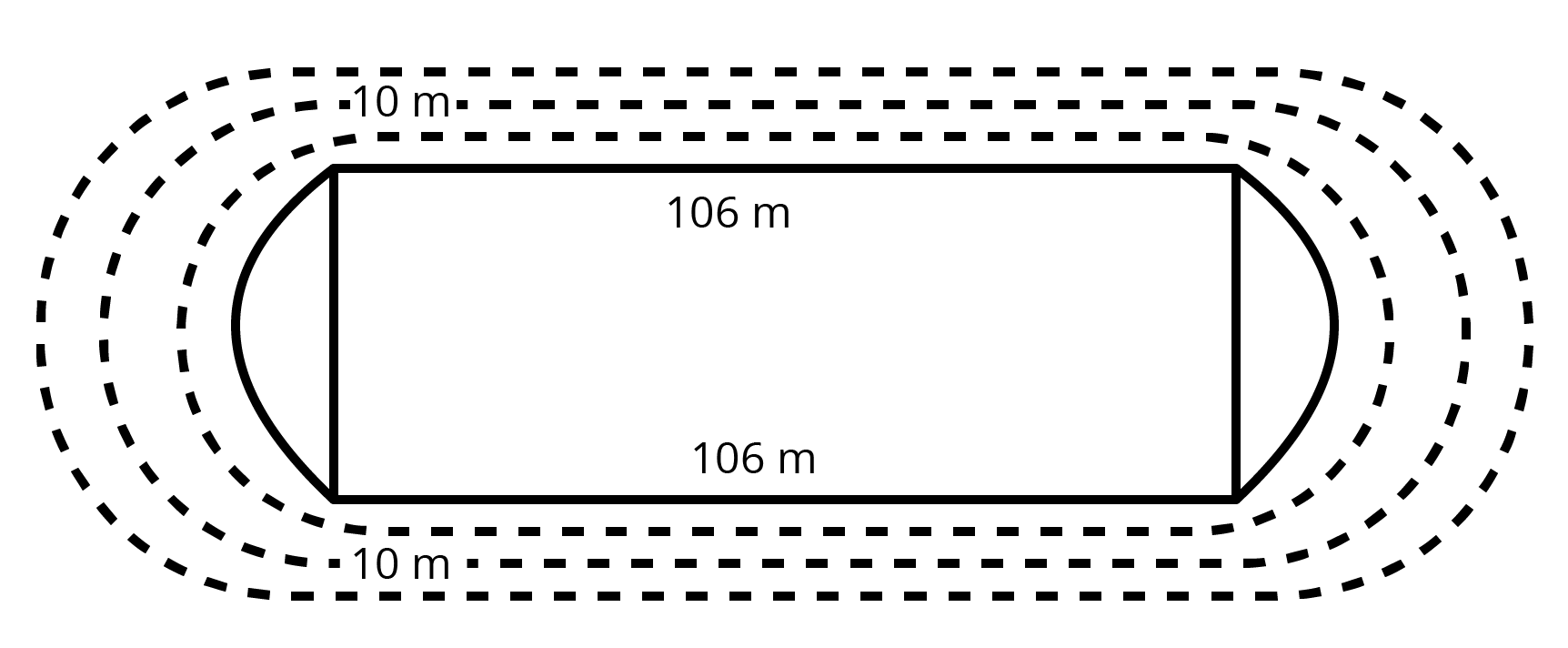
(i). The distance around the track along its inner edge.
Ans: (i) The distance around the track along the inner edge:
\[\Rightarrow 106+106+(\pi \times 30+\pi \times 30)\]
\[\Rightarrow 212+\dfrac{22}{7}\times 60\]
\[\Rightarrow \dfrac{2804}{7}m\]
(ii). The area of the track.
Ans. (ii) The area of the track:
\[\Rightarrow 106\times 80-106\times 60+2\dfrac{1}{2}\pi [{{40}^{2}}-{{30}^{2}}]\]
\[\Rightarrow 106\times 20+\pi (70)(10)\]
\[\Rightarrow 12+700\times \dfrac{22}{7}\]
\[\Rightarrow 4320{{m}^{2}}\]
26. Which of the following are APs? If they form an AP, find the common difference \[d\] and write three more terms.
(i) \[2,4,8,16,...\]
Ans: (i) \[2,4,8,16,...\]
It is not an AP because difference between consecutive terms is not equal.
As \[4-2\ne 8-4\]
(ii) \[2,\dfrac{5}{2},3,\dfrac{7}{2},...\]
Ans. (ii) \[2,\dfrac{5}{2},3,\dfrac{7}{2},...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow \dfrac{5}{2}-2=\dfrac{1}{2}\]
Common difference: \[d=\dfrac{1}{2}\]
Fifth term: \[\dfrac{7}{2}+\dfrac{1}{2}=4\]
Sixth term: \[4+\dfrac{1}{2}=\dfrac{9}{2}\]
Seventh term: \[\dfrac{9}{2}+\dfrac{1}{2}=5\]
Therefore, next three terms are \[4,\dfrac{9}{2},5\] .
(iii) \[-1.2,-3.2,-5.2,-7.2,...\]
Ans. (iii) \[-1.2,-3.2,-5.2,-7.2,...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow -3.2+1.2=-2\]
Common difference: \[d=-2\]
Fifth term: \[-7.2-2=-9.2\]
Sixth term: \[-9.2-2=-11.2\]
Seventh term: \[-11.2-2=-13.2\]
Therefore, next three terms are \[9.2,-11.2,-13.2\] .
(iv) \[-10,-6,-2,2,...\]
Ans. (iv) \[-10,-6,-2,2,...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow -6+10=4\]
Common difference: \[d=4\]
Fifth term: \[2+4=6\]
Sixth term: \[6+4=10\]
Seventh term: \[10+4=14\]
Therefore, next three terms are \[6,10,14\] .
(v) \[3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2}...\]
Ans. (v) \[3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2}...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow 3+\sqrt{2}-3=\sqrt{2}\]
Common difference: \[d=\sqrt{2}\]
Fifth term: \[3+3\sqrt{2}+\sqrt{2}=3+4\sqrt{2}\]
Sixth term: \[3+4\sqrt{2}+\sqrt{2}=3+5\sqrt{2}\]
Seventh term: \[3+5\sqrt{2}+\sqrt{2}=3+6\sqrt{2}\]
Therefore, next three terms are \[3+4\sqrt{2},3+5\sqrt{2},3+6\sqrt{2}\] .
(vi) \[0.2,0.22,0.222,0.2222,...\]
Ans: (vi) \[0.2,0.22,0.222,0.2222,...\]
It is not an AP because difference between consecutive terms is not equal.
As \[0.222-0.22\ne 0.22-0.2\]
(vii) \[0,-4,-8,-12,...\]
Ans. (vii) \[0,-4,-8,-12,...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow -4-0=-4\]
Common difference: \[d=-4\]
Fifth term: \[-12-4=-16\]
Sixth term: \[-16-4=-20\]
Seventh term: \[-20-4=-24\]
Therefore, next three terms are \[-16,-20,-24\] .
(viii) \[-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2},...\]
Ans. (viii) \[-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2},...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow -\dfrac{1}{2}+\dfrac{1}{2}=0\]
Common difference: \[d=0\]
Fifth term: \[-\dfrac{1}{2}+0=-\dfrac{1}{2}\]
Sixth term: \[-\dfrac{1}{2}+0=-\dfrac{1}{2}\]
Seventh term: \[-\dfrac{1}{2}+0=-\dfrac{1}{2}\]
Therefore, next three terms are \[-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2}\] .
(ix) \[1,3,9,27,...\]
Ans: (ix) \[1,3,9,27,...\]
It is not an AP because difference between consecutive terms is not equal.
As \[3-1\ne 9-3\]
(x) \[a,2a,3a,4a,...\]
Ans. (x) \[a,2a,3a,4a,...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow 2a-a=a\]
Common difference: \[d=a\]
Fifth term: \[4a+a=5a\]
Sixth term: \[5a+a=6a\]
Seventh term: \[6a+a=7a\]
Therefore, next three terms are \[5a,6a,7a\] .
(xi) \[a,{{a}^{\mathbf{2}}},{{a}^{\mathbf{3}}},{{a}^{\mathbf{4}}}...~\]
Ans: (xi) \[a,{{a}^{\mathbf{2}}},{{a}^{\mathbf{3}}},{{a}^{\mathbf{4}}}...~\]
It is not an AP because difference between consecutive terms is not equal.
As \[{{a}^{2}}-a\ne {{a}^{3}}-{{a}^{2}}\]
(xii) \[\sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},...\]
Ans. (xii) \[\sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},...\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow 2\sqrt{2}-\sqrt{2}=\sqrt{2}\]
Common difference: \[d=\sqrt{2}\]
Fifth term: \[4\sqrt{2}+\sqrt{2}=\sqrt{50}\]
Sixth term: \[5\sqrt{2}+\sqrt{2}=\sqrt{72}\]
Seventh term: \[6\sqrt{2}+\sqrt{2}=\sqrt{98}\]
Therefore, next three terms are \[\sqrt{50},\sqrt{72},\sqrt{98}\] .
(xiii) \[\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...\]
Ans: (xiii) \[\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...\]
It is not an AP because difference between consecutive terms is not equal.
As \[\sqrt{6}-\sqrt{3}\ne \sqrt{9}-\sqrt{6}\]
(xiv) \[{{1}^{2}},{{3}^{2}},{{5}^{2}},{{7}^{2}}...~\]
Ans: (xiv) \[{{1}^{2}},{{3}^{2}},{{5}^{2}},{{7}^{2}}...~\]
It is not an AP because difference between consecutive terms is not equal.
As \[9-1\ne 25-9\]
(xv) \[{{1}^{2}},{{5}^{2}},{{7}^{2}},73...~\]
Ans. (xv) \[{{1}^{2}},{{5}^{2}},{{7}^{2}},73...~\]
It is an AP because difference between consecutive terms is equal.
\[\Rightarrow 25-1=24\]
Common difference: \[d=24\]
Fifth term: \[73+24=97\]
Sixth term: \[97+24=121\]
Seventh term: \[121+24=145\]
Therefore, next three terms are \[24,121,145\] .
Class 10 Maths Chapter 5 Extra Questions – PDF Download
Vedantu provides a free downloadable PDF version of Chapter 5 Maths Class 10 important questions for the students. It is easily accessible by all the students on any devices, and is also easily downloadable for future offline reference on any device, without any limitations. Along with the important questions, the PDF also carries the solutions for each problem, and some alternative solutions to help the students.
Chapter 5 of Maths Class 10 is about the Arithmetic progression that is a vast chapter and has various applications and extended studies in the higher classes. Therefore, the students need to practice all the questions available in the PDF of important questions of Chapter 5 Maths Class 10 to briefly discuss the problems that are important for all the examinations and the ones that require more practice. This is also helpful as the students can access them anytime and anywhere.
Class 10 Maths Ch 5 Important questions help the students get well-versed with all the concepts and be confident about solving various types of problems related to a given concept. This is a significant reason why it is always advised that the students practice more questions from different sets of Class 10, Chapter 5 important questions.
Important Questions for Class 10 Maths Arithmetic Progression – Related Essential Concepts
Arithmetic Progression has many topics from which the questions are asked in the examinations. Here are the major topics that cover some questions in several examinations and whose problems are also included in the set of important questions for Class 10 Maths Chapter 5.
Series, Sequence, and Progressions
A series refers to the Sum of elements in a given sequence, as the Sum of n natural numbers is the series of n natural numbers. On the other hand, a sequence refers to a list of finite or infinite numbers which follows a specific pattern, like the numbers 1, 2, 3, 4, 5,… is an endless sequence of natural numbers. Each number coming in a series or a sequence is known as a term. Furthermore, a progression refers to a sequence where the general term is expressible using a mathematical formula.
Arithmetic Progression
Arithmetic Progression refers to a progression where the difference between any two consecutive numbers of the concerned sequence is always constant. Any AP has a general form as a, a+d, a+2d, a+3d, a+4d… where a is the first term of the given sequence and d is a common difference.
Arithmetic Progression can be finite as well as infinite. Finding the last term for a finite AP is feasible, whereas it is not for an infinite AP.
Common Difference
For a given sequence in an AP, the difference between any two consecutive terms is always constant. This difference refers to the "common difference" (d) of the concerned AP. According to the given scenario, the common difference (d) for a given AP can be:
Positive, for an increasing AP.
Zero, for a constant AP.
Negative, for a decreasing AP.
n
th
Term and Sum of n Terms of an AP
For a given AP, the nth term is given as Tn = a+ (n−1)d. Here, a refers to the AP's first term, d is a common difference, and n is the number of terms of it.
On the other hand, the Sum of n terms for a given AP is given as Sn=n/2(2a+(n−1)d). Here, a refers to the first term of the concerned AP, d is the common difference and n is the number of terms for which the Sum is calculated. Sum of the given AP can also be computed using Sn=n/2(a+l). Here, a is the first term of the given AP, l is its last term, and n is the total number of terms considered.
Arithmetic Mean (AM)
Arithmetic Mean of the given numbers is simply the average of them. Or a given set of numbers,
Arithmetic Mean = Sum of terms/Number of terms
For defining the arithmetic mean of the given numbers, they are not required to be in an AP.
Sum of First n Natural Numbers
For a given range of up to n, the Sum of n natural numbers is given by:
Sn=n(n+1)/2
To derive this formula of Sum of n natural numbers, one must consider the given natural numbers sequence as an AP, with the first term as one and common difference as 1.
Class 10 Maths Chapter 5 Important Questions
Based on the surveys done on previous year Boards examination papers and competitive level examinations, Vedantu experts designed Arithmetic Progression Class 10 important questions for the students. The top ten questions from the entire set of Arithmetic progression important questions are as follows:
For a given AP: 21, 18, 15, ....., which term is -81? Also, tell whether any of the terms is 0 or not? Justify the answers.
For a given AP: 11, 8, 5, 2, check whether 150 is the term associated with it or not.
For a given AP, the third term is four and the 9th term is -8. Find out whether any of its terms is zero. Also, find the term which is 0.
For a given AP: 3, 15, 27, 39, ..., write the difference between the 54th term of the AP and the number 132. Is 132 greater than the 54th term of the AP?
Write the number of multiples of 4 lying between 10 and 250.
For a given AP, the Sum of 4th and 8th term is 24, and that of 6th and 10th term is 44. Calculate the first five terms of the AP.
Shiva saved 5 INR in the first week of the year and increased her weekly savings by 1.75 INR every week. If his saving is 20.75 INR in the nth week, find n.
For a given AP: 24, 21, 18,..., how many terms are essential for making the Sum as 78?
For an AP, the first term is 5, and the last is 45. The Sum of all the terms is 400. Find the common difference and the number of terms.
For a given AP, the Sum of 3rd and 7th term is 6, and the product is 8. Find the Sum of the first sixteen terms of the given AP.
Practice Questions for Class 10 Maths Chapter 5: Arithmetic Progression
The following are some of the questions that can be taken up by students to assist them in the board preparations.
Question 1. A total of Rs 700 would be used to provide seven cash prizes to pupils for their overall academic performance at a school. Determine the value of each reward if it is Rs 20 less than the prize before it.
Answer. 160, Rs 140, Rs 120, Rs 100, Rs 80, Rs 60 and Rs 40 are the correct answers.
Question 2. Find the 9th term from the end of the A.P. 5,9,13,..., 185 towards the first term.
Answer. 153 (Using the formula an = a + (n-1)d).
Question 3. The angles of a triangle are measured in A.P., with the smallest angle being half of the largest. Determine the angles.
Answer. 40, 60, and 80 are the correct answers.
Question 4. In the series of AP 4, 9, 14, 19,..., which term is 109?
Answer. 22nd term.
Question 5. Find the AP, if the sum of the first seven terms of an AP is 182. Given that the 4th and 17th terms are in the ratio 1: 5.
Answer. AP would be 2, 10, 18, 26, …. .
Benefits of Important Questions for Class 10 Maths Chapter 5:
Crucial in student preparation, Class 10 Maths Chapter 5 important questions serve as a pivotal study and revision resource. These essential questions enhance understanding and contribute significantly to exam success in Arithmetic Progression. The key benefits of engaging with these important questions include:
Comprehensive Preparation:
Important questions for Class 10 Maths Chapter 5 in Arithmetic Progression compile frequently asked and diverse question types.
Offer students a consolidated study material for better preparation.
Insights and Approaches:
Provide an in-depth understanding of question types and various approaches to solve them.
Equip students with knowledge on handling different types of problems effectively.
Confident Exam Appearance:
Enable students to confidently appear in exams with the desired level of practice.
Contribute to successful exam outcomes and performance with flying colors.
Versatile Practice:
Beneficial for both school and competitive level examinations.
Include alternative approaches for problem-solving in different scenarios.
Extra Load of Practice:
Serve as an additional resource for extra practice in mathematics.
Acknowledge the importance of consistent practice for successful outcomes.
Important Related Links for CBSE Class 10 Maths
Conclusion
Vedantu's mission is to support students nationwide in their exam preparations. All our study resources, including "Important Questions for CBSE Class 10 Maths Chapter 5 - Arithmetic Progressions," are freely available for download in PDF format. Our experts provide sample responses for each question in CBSE Class 10 test papers, enabling students to practice independently. Utilizing the Vedantu Website and App, students can access essential questions, revision notes, NCERT chapter-wise solutions, and other necessary materials related to Chapter 5. This inclusive approach ensures that valuable resources are accessible to all, fostering effective and holistic learning experiences.
FAQs on Important Questions for CBSE Class 10 Maths Chapter 5 - Arithmetic Progressions
Q1. Is Chapter 5 Arithmetic Progression of Class 10 Maths easy?
Ans: Chapter 5 Arithmetic Progression of Class 10 Maths is easy provided that you follow the right strategy and study plan to simplify your preparation for this chapter. Before solving the exercise questions, first, read the theory and obtain the basic conceptual understanding of the arithmetic progression and the related terms. Then, go through the solved examples to understand the stepwise method of answering each type of question. Next, solve all the NCERT questions and clear all doubts as soon as possible. Revise the chapter multiple times to make this chapter easy for you.
Q2. How can I prepare Chapter 5 Arithmetic Progression of Class 10 Maths?
Ans: The first step to prepare Class 10 Maths, Chapter 5- Arithmetic Progression is to solve every question and example of this chapter from the NCERT standard Maths textbook. Clear all doubts as soon as possible to ensure a clear and smooth Maths exam preparation journey. Lastly, practice questions from the past year question papers from this chapter and give timed mock tests to build confidence and manage time well in the exam. If you follow this strategy diligently, you will master this chapter and perform well in the Maths exam.
Q3. What is Arithmetic Progression according to Chapter 5 Arithmetic Progression of Class 10 Maths?
Ans: As discussed in the chapter, Arithmetic Progression, in simple words, refers to a mathematical sequence in a particular order in which the difference between two consecutive terms is a fixed number throughout the sequence. For instance, the series of natural numbers are in Arithmetic Progression because the difference between two consecutive terms is the same throughout the sequence.
These solutions are available on Vedantu's official website(vedantu) and mobile app free of cost.
Q4. What are the most important topics in Chapter 5 Arithmetic Progression of Class 10 Maths?
Ans: Class 10 Maths, Chapter 5- Arithmetic Progression, as the name suggests, deals with the study of arithmetic progression and related concepts. The most important topics in this chapter are- the difference between a sequence, a series and an arithmetic progression, the terms in an AP, the common difference between the terms in an AP, the nth term in an AP, the general form and the sum of n terms in an AP.
Q5. Where can I find the most important questions for Chapter 5 Arithmetic Progression of Class 10 Maths?
Ans: Refer to Vedantu's Important Questions for Class 10 Maths, Chapter 5- Arithmetic Progression by clicking here. It covers all the most important questions of Arithmetic Progression from an examination point of view. These questions have been prepared by the best Maths teachers in India after deeply analyzing the previous year Board exam questions, latest Maths syllabus and exam pattern. If you thoroughly prepare these questions, you will be an expert in this chapter and will surely fetch high marks in the Maths exam.