CBSE Class 11 Maths Important Questions - Chapter 11 Introduction to Three Dimensional Geometry

1 Marks Questions

1.Name the octant in which the following lie: $(5,2,3)$

Ans: Octant I

2. Name the octant in which the following lie: $( - 5,4,3)$

Ans: Octant II

3. Find the image of $( - 2,3,4)$ in the y $z$ plane

Ans: $(2,3,4)$

4. Find the image of $(5,2, - 7)$ in the x y plane.

Ans: $(5,2,7)$

5. A point lie on ${\mathbf{X}}$-axis what are co- ordinate of the point

Ans: $(a,0,0)$

6. Write the name of plane in which $x$ axis and $y$- axis are taken together.

Ans: X Y Plane

7. The point $(4, - 3, - 6)$ lie in which octants

Ans: VIII

8. The point $(2,0,8)$ lie in which plane

Ans: XZ Plane

9. A point is in the $XZ$ plane. What is the value of y co-ordinates?

Ans: $Zero$

10. What is the coordinates of $XY$ plane

Ans: $(x,y,0)$

11. The point $( - 4,2,5)$ lie in which octant.

Ans:  Octant II

12. The distance from origin to point $(a,b,c)$ is:

Ans: Distance from origin=$\sqrt {{a^2} + {b^2} + {c^2}} $

4 Marks Questions

1. Given that $P(3,2, - 4),Q(5,4, - 6)$ and $R(9,8, - 10)$ are collinear. Find the ratio in which $Q$ divides PR

Ans: Suppose Q divides PR in the ratio $\lambda :1.$ Then coordinator of ${\text{Q}}$ are

$\left( {\dfrac{{9\lambda  + 3}}{{\lambda  + 1}},\dfrac{{8\lambda  + 2}}{{\lambda  + 1}},\dfrac{{ - 10\lambda  - 4}}{{\lambda  + 1}}} \right)$

But, coordinates of ${\text{Q}}$ are $(5,4, - 6).$Therefore

$\dfrac{{9\lambda  + 3}}{{2 + 1}} = 5,\dfrac{{8\lambda  + 2}}{{\lambda  + 1}} = 4,\dfrac{{ - 10\lambda  - 4}}{{2 + 1}} = 6$

These three equations give

$\hat \alpha  = \dfrac{1}{2}$

So Q divides PR in the ratio $\dfrac{1}{2}:1$ or 1:2

2. Determine the points in x y plane which is equidistant from these point A $(2,0,3)$T${\text{B}}(0,3,2)$ and $C(0,0,1)$

Ans: Since the z coordinate in the xy plane is zero. So, let P(x, y, 0) be a point in xy- plane, such that PA=PB=PC. $Now,PA = PB$

PA2 = PB2

$ \Rightarrow {(x - 2)^2} + {(y - 0)^2} + {(0 - 3)^2} = {(x - 0)^2} + {(y - 3)^2} + {(0 - 2)^2}$

$2x - 3y = 0 \ldots ..(i)$

$PB = PC$

$ \Rightarrow P{B^2} = P{C^2}$

$ \Rightarrow {(x - 0)^2} + {(y - 3)^2} + {(0 - 2)^2} = {(x - 0)^2} + {(y - 0)^2} + {(0 - 1)^2}$T

$ \Rightarrow  - 6y + 12 = 0 \Rightarrow y = 2 \ldots  \ldots ..(ii)$

Put $y = 2$ in (i) we get $x = 3$

Hence the points required are $(3,2,0)$.

3. Find the locus of the point which is equidistant from the point ${\text{A}}(0,2,3)$ and ${\text{B}}(2, - 2,1)$

Ans: Let \[Q(x,y,z)\]be any point which is equidistant from $A(0,2,3)$ and $B(2, - 2,1).$ Then

\[QA = QB\]

Squaring both sides, we get

\[QA\]2 = \[QB\]2

$ \Rightarrow \sqrt {{{(x - 0)}^2} + {{(y - 2)}^2} + {{(2 - 3)}^2}}  = \sqrt {{{(x - 2)}^2} + {{(y + 2)}^2} + {{(z - 1)}^2}} $

$\Rightarrow 4x - 8y - 42 + 4 = 0$

$\Rightarrow x - 2y - 2 + 1 = 0$

$\Rightarrow x - 2y - 1 = 0$

4. Show that the points\[P(2, - 1,3),Q(0,1,2),R(2, - 1,3)\]  are vertices of an isosceles right angled triangle.

Ans: We have

$PQ = \sqrt {{{(2 - 0)}^2} + {{( - 1 - 1)}^2}{{( + 3 - 2)}^2}}  = \sqrt {4 + 4 + 1}  = 3$

$QR = \sqrt {{{(1 - 2)}^2} + {{( - 3 + 1)}^2} + {{(1 - 3)}^2}}  = \sqrt {1 + 4 + 4}  = 3$

And $RP = \sqrt {{{(1 - 0)}^2} + {{( - 3 - 1)}^2} + {{(1 - 2)}^2}}  = \sqrt {1 + 16 + 1}  = 3\sqrt 2 $

Clearly $PQ = QR$ and $PQ$2 + $QR$2 = $RP$2

Hence triangle $PQR$ is an isosceles right angled triangle.

5. Using the section formula, prove that the three points $A( - 2,3,5), B(1,2,3)$, and $C(7,0, - 1)$ are collinear.

Ans: Assume that the given points are collinear and $C$ divides $AB$ in the ratio $\lambda  = 1.$

Then coordinates of $C$ are

$\left( {\dfrac{{\lambda  - 2}}{{2 + 1}},\dfrac{{2\lambda  + 3}}{{\lambda  + 1}},\dfrac{{3\hat 2 + 5}}{{\lambda  + 1}}} \right)$

But the coordinates of $C$ are $(3,0, - 1)$ from the above equations we get $\lambda  = \dfrac{3}{2}$

Since these equation give the same value of ${V_.}$

∴  the given points are collinear and$C$ divides $AB$ exactly in the ratio 3: 2.

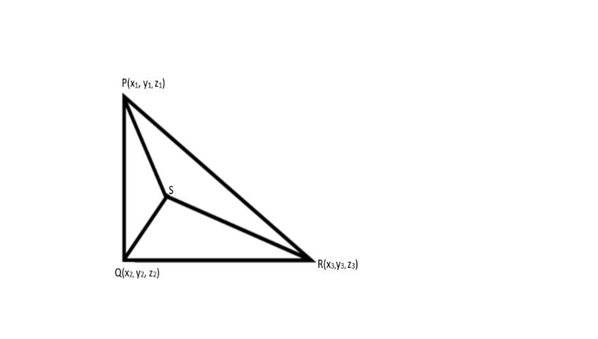
6. Show that coordinator of the centroid of triangle with vertices $A\left( {{x_1}{y_1}{z_1}} \right),{\text{B}}\left( {{x_2}{y_2}{z_2}} \right)$,T$\operatorname{and} C\left( {{x_3}{y_3}{z_3}} \right)$ is $\left[ {\dfrac{{{x_1} + {y_1} + {z_1}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right]$

Ans: Let $D$ be the mid-point of $BC$ ,then

Coordinates of ${\text{D}}$are $\left( {\dfrac{{{x_2} + {x_2}}}{2},\dfrac{{{y_2} + {y_3}}}{2},\dfrac{{{z_2} + {z_3}}}{2}} \right)$. 

Let${\text{G}}$ be the centroid of $\vartriangle ABC$. The ${\text{G}}$, divides${\text{AD}}$ in the ratio 2:  1. So coordinates of ${\text{D}}$are

$\left( {\dfrac{{1.{x_1} + 2\dfrac{{\left( {{x_2} + {x_3}} \right)}}{2}}}{{1 + 2}} \cdot \dfrac{{{{1.2}_1} + 2\left( {\dfrac{{{y_2} + {y_3}}}{2}} \right)}}{{1 + 2}} = \dfrac{{1 - {z_1} + 2\left( {\dfrac{{{z_2} + {z_3}}}{2}} \right)}}{{1 + 2}}} \right)$

$\left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)$

7. Prove by distance formula that the points $X(1,2,3),Y( - 1, - 1, - 1),Z(3,5,7)$ are collinear.

Ans: The Distance

$|XY| = \sqrt {{{( - 1 - 1)}^2} + {{( - 1 - 2)}^2} + {{( - 1 - 3)}^2}}  = \sqrt {4 + 9 + 16}  = \sqrt {29} $

Distance

$|YZ| = \sqrt {{{(3 + 1)}^2} + {{(5 + 1)}^2} + {{(7 + 1)}^2}}  = \sqrt {16 + 36 + 64}  = 2\sqrt {29} $

Distance

$|XZ| = \sqrt {{{(3 - 1)}^2} + {{(5 - 2)}^2} + {{(7 - 3)}^2}}  = \sqrt {4 + 9 + 16}  = \sqrt {29} $

$\therefore |YZ| = |XY| + |XZ|$

The points $X,Y,Z$ are collinear.

8. find the co-ordinate of the point which divides the join of $A(2, - 1,4),B(4,3,2)$ in the ratio $2:5(i)$ internally (ii) externally

Ans: Let $C(x,y,z)$ be the required point

i. For internal division

$x = \dfrac{{2 \times 4 + 5 \times 2}}{{2 + 5}} = \dfrac{{8 + 10}}{7} = \dfrac{{18}}{7}$

$y = \dfrac{{2 \times 3 + 5 \times  - 1}}{{2 + 5}} = \dfrac{{6 - 5}}{7} = \dfrac{1}{7}$

$z = \dfrac{{2 \times 2 + 5 \times 4}}{{2 + 5}} = \dfrac{{4 + 20}}{7} = \dfrac{{24}}{7}$

$\therefore $Required point$C\left( {\dfrac{{18}}{7},\dfrac{1}{7},\dfrac{{24}}{7}} \right)$

ii. For external division.

$x = \dfrac{{2 \times 4 - 5 \times 2}}{{2 - 5}} = \dfrac{{8 - 10}}{{ - 3}} = \dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3}$

$y = \dfrac{{2 \times 3 - 5 \times  - 1}}{{2 - 5}} = \dfrac{{6 + 5}}{{ - 3}} = \dfrac{{11}}{{ - 3}}$

$z = \dfrac{{2 \times 2 - 5 \times 4}}{{2 - 5}} = \dfrac{{4 - 20}}{{ - 3}} = \dfrac{{ - 16}}{{ - 3}} = \dfrac{{16}}{3}$

$\therefore $Required point $C\left( {\dfrac{2}{3},\dfrac{{ - 11}}{3},\dfrac{{16}}{3}} \right)$

9. Find the co-ordinate of a point equidistant from the four points

$P(0,0,0),Q(a,0,0),R(0,b,0)$ and $S(0,0,c)$.

Ans: let $A(x,y,z)$ be the required point

According to condition

$PA = AQ = AR = AS$

Now $PA = AQ$

$ \Rightarrow P{A^2} = A{Q^2}$

$ \Rightarrow {x^2} + {y^2} + {z^2} = {(x - a)^2} + {(y - 0)^2} + {(z - 0)^2}$

$ \Rightarrow {x^2} + {y^2} + {z^2} = {x^2} - 2ax + {a^2} + {y^2} + {z^2}$

$2ax = {a^2}$

$\therefore x = \dfrac{a}{2}$

Similarly $PA = AR$

$ \Rightarrow y = \dfrac{b}{2}$

$Q\left( {x,y,{z_,}} \right)\quad ,R\left( {{x_2},{y_2},{z_2}} \right)$ and $S\left( {{x_3},{y_3},{z_3}} \right)D,E$ and $F$ are mid points of side $RS,SQ$ and $QR$ respectively.

Then $\dfrac{{{x_1} + {x_2}}}{2} =  - 1$

${x_1} + {x_2} =  - 2 \ldots ..(1)$

$\dfrac{{{y_1} + {y_2}}}{2} = 1$

${y_1} + {y_2} = 2 \ldots  \ldots $(2)

$\dfrac{{{z_1} + {z_2}}}{2} =  - 4$

${z_1} + {z_2} =  - 8 \ldots  \ldots (3)$

$\dfrac{{{x_2} + {x_3}}}{2} = 1$

${x_2} + {x_3} = 2 \ldots  \ldots (4)$

$\dfrac{{{y_2} + {y_3}}}{2} = 2$

$y2 + y3 = 4 \ldots ..(5)$

$\dfrac{{{z_2} + {z_3}}}{2} =  - 3$

${z_2} + {z_3} =  - 6 \ldots  \ldots $(6)

$\dfrac{{{x_1} + {r_3}}}{2} = 3$

${x_1} + {x_3} = 6 \ldots  \ldots (7)$

$\dfrac{{{y_1} + {y_3}}}{2} = 0$

${y_1} + {y_3} = 0 \ldots  \ldots (8)$

$\dfrac{{{z_1} + {z_3}}}{2} = 1$

${z_1} + {z_3} = 2 \ldots  \ldots (9)$

Adding equation (1), (4) and (7) we get

$2\left( {{y_1} + {y_2} + {y_3}} \right) = 6$

${y_1} + {y_2} + {y_3} = 3 \ldots  \ldots (11)$

And $PA = AS$

$ \Rightarrow z = \dfrac{c}{2}$

Hence co-ordinate of $A(\dfrac{a}{2},\dfrac{b}{2},\dfrac{c}{2})$

10. Find the ratio in which the join the $B(2,1,5)$ and $C(3,4,3)$ is divided by the plane$2x + 2y - 2z = 1$. Also find the co-ordinate of the point of division.

Ans: Assume the plane$2x + 2y - 2z = 1$ divides $A(2,1,5)$ and $B(3,4,5)$ in the ratio $\lambda :1$ at point $A$

Then the co-ordinate of the point $A$

$\left( {\dfrac{{3\lambda  + 2}}{{\lambda  + 1}} \cdot \dfrac{{4\lambda  + 1}}{{\lambda  + 1}}\dfrac{{3\lambda  + 5}}{{\lambda  + 1}}} \right)$

$\because $ Point $A$ lies on the plane $2x + 2y - 2z = 1$

$\therefore $ Points $A$ must satisfy the equation of plane

$2\left( {\dfrac{{3\lambda  + 2}}{{\lambda  + 1}}} \right) + 2\left( {\dfrac{{4\lambda  + 1}}{{\lambda  + 1}}} \right) - 2\left( {\dfrac{{3\lambda  + 5}}{{\lambda  + 1}}} \right) = 1$

$ \Rightarrow 8\lambda  - 4 = \lambda  + 1$

$ \Rightarrow \lambda  = \dfrac{5}{7}$

$\therefore $ Required ratio 5:7

11. Find the centroid of a triangle, mid-points of whose sides are $D(1,2, - 3),E(3,0,1)$and$F( - 1,1, - 4)$.

Ans: Suppose the co-ordinate of vertices of $\vartriangle ABC$ are

Add equation (3), (6) and (9)

$2\left( {{z_1} + {z_2} + {z_3}} \right) =  - 8 - 6 + 2$

${z_1} + {z_2} + {z_3} =  - 6 \ldots  \ldots (12)$

Co-ordinate of centroid

$x = \dfrac{{{x_1} + {x_2} + {x_3}}}{3} = \dfrac{3}{3} = 1$

$y = \dfrac{{{y_1} + {y_2} + {y_3}}}{3} = \dfrac{3}{3} = 1$

$z = \dfrac{{{z_1} + {z_2} + {z_3}}}{3} = \dfrac{{ - 6}}{3} =  - 2$

$(1,1, - 2)$

12. The mid points of the sides of $\vartriangle ABC$ are given by $( - 2,3,5),(4, - 1,7)$ and $(6,5,3)$ find the co-ordinate of ${\text{A}},{\text{B}}$ and${\text{C}}$.

Ans: Let us suppose that the co-ordinates of point $A,B$ AND $C$ are $\left( {{x_1},{y_1},{z_1}} \right),\left( {{x_2},{y_2},{z_2}} \right)$and $\left( {{x_3},{y_3},{z_3}} \right)$ respectively. Let $D,E$ and$F$are the mid-points of side $BC,CA$and $AB$respectively.

$x$1 + $x$2 =12T………(1)

$\dfrac{{{y_1} + {y_2}}}{2} = 5$

${y_1} + {y_2} = 10 \ldots  \ldots (2)$

$\dfrac{{{z_1} + {z_2}}}{2} = 3$

${z_1} + {z_2} = 6 \ldots  \ldots $(3)

$\dfrac{{{x_2} + {x_3}}}{2} =  - 2$

${x_2} + {x_3} =  - 4 \ldots  \ldots (4)$

$\dfrac{{{y_2} + {y_3}}}{2} = 3$

${y_2} + {y_3} = 6 \ldots  \ldots (5)$

$\dfrac{{{z_1} + {z_2}}}{2} = $

${z_1} + {z_2} = 10 \ldots  \ldots (6)$

$\dfrac{{{x_1} + {x_3}}}{2} = 4$

${x_1} + {x_3} = 8 \ldots  \ldots (7)$

$\dfrac{{{y_1} + {y_3}}}{2} =  - 1$

${y_1} + {y_3} =  - 2 \ldots  \ldots $(8)

$\dfrac{{{z_1} + {z_3}}}{z} = 7$

${z_1} + {z_3} = 14 \ldots  \ldots $(9)

Add equation (1), (4) and (7)

$2\left( {{x_1} + {x_2} + {x_3}} \right) = 12 - 4 + 8$

${x_1} + {x_2} + {x_3} = \dfrac{{16}}{3} = 8 \ldots ..(10)$

Similarly,${y_1} + {y_2} + {y_3} = 7 \ldots  \ldots (11)$

${z_1} + {z_2} + {z_3} = 15 \ldots  \ldots (12)$

Subtract equation (1), (4) and (7) from (10)

${x_3} =  - 4,\quad {x_1} = 12,\quad {x_2} = 0$

Now subtract equation (2), (5) and (8) from (11)

${y_3} =  - 3,\quad {y_1} = 1,\quad {y_2} = 9$

Similarly,${z_3} = 9,\quad {z_1} = 5,\quad {z_2} = 1$

$\therefore $ co-ordinate of point $A,B$and $C$are

$A(12,0, - 4),B(1,9, - 3)$ ,and$C(5,1,9)$

13. Find the co-ordinates of the points which trisects the line segment $QP$ formed by joining the point $P(4,2, - 6)$ and $Q(10, - 16,6)$.

Ans: Let $R\& S$ be the points of trisection of the line  segment $QP$ . Then

$ \Rightarrow 2PR = RQ$

$ \Rightarrow \dfrac{{PQ}}{{RQ}} = \dfrac{1}{2}$

∴ $S$divide $QP$in the ratio 1: 2

$\therefore $ Co-ordinates of point

$S\left[ {\dfrac{{1(10) + 2 \times 4}}{{1 + 2}},\dfrac{{1( - 16) + 2 \times 2}}{{1 + 2}},\dfrac{{1 \times 6 + 2( - 6)}}{{1 + 2}}} \right]$

$S(6, - 4, - 2)$

Similarly,$PS = 2SQ$

$ \Rightarrow \dfrac{{PS}}{{SQ}} = \dfrac{2}{1}$

$\therefore $$R$ divide the line segment $QP$ in the ratio 2:1

$\therefore $ co-ordinates of point $R$

$R\left[ {\dfrac{{2(10) + 1(4)}}{{1 + 2}},\dfrac{{2( - 16) + 1(2)}}{{1 + 2}},\dfrac{{2(6) + 1( - 6)}}{{1 + 2}}} \right]$

$\therefore R(8, - 10,2)$

14. Show that the point $A(1,2,3),B( - 1, - 2, - 1),C(2,3,2)$ and $D(4,7,6)$ taken in order form the vertices of a parallelogram. Do these form a rectangle?

Ans: Mid-point of $AC$ is $\left( {\dfrac{{1 + 2}}{2},\dfrac{{2 + 3}}{2},\dfrac{{3 + 2}}{2}} \right)$

i.e. $\left( {\dfrac{3}{2},\dfrac{5}{2},\dfrac{5}{2}} \right)$

also the mid-point of $BD$ is $\left( {\dfrac{{ - 1 + 4}}{2},\dfrac{{ - 2 + 7}}{2},\dfrac{{ - 1 + 6}}{2}} \right)$

i.e.$\left( {\dfrac{3}{2},\dfrac{5}{2},\dfrac{5}{2}} \right)$

Then$AC$and  $BD$ have same mid-points

$\therefore $$AC$ and $BD$ bisect each other , It is a Parallelogram.

Now 

$AC = \sqrt {{{(2 - 1)}^2} + {{(3 - 2)}^2} + {{(2 - 3)}^2}}  = \sqrt 3 $ and

$BD = \sqrt {{{(4 + 1)}^2} + {{(7 + 2)}^2} + {{(6 + 1)}^2}}  = \sqrt {155} $

$\therefore AC \ne BD$ diagonals are not equal

PQRS is not a rectangle.

15. A point $C$with $x$ co-ordinates 4 lies on the line segment joining the points$A(2, - 3,4)$ and $B(8,0,10)$ find the co-ordinates of the point $C$.

Ans: let the point $C$ divide the line segment joining the point $A$ and $B$in the ratio $\lambda  = 1$, Then co-ordinates of Point ${\text{R}}$

$\left[ {\dfrac{{8\lambda  + 2}}{{\lambda  + 1}},\dfrac{{ - 3}}{{\lambda  + 1}},\dfrac{{10\lambda  + 4}}{{\lambda  + 1}}} \right]$

The $x$ co-ordinates of point $C$is 4

$ \Rightarrow \dfrac{{8\lambda  + 2}}{{\lambda  + 1}} = 4 = \lambda  = \dfrac{1}{2}$

$\therefore $ co-ordinates of point ${\text{R}}$

$\left[ {4,\dfrac{{ - 3}}{{\dfrac{1}{2} + 1}} \cdot \dfrac{{10 \times \dfrac{1}{2} + 4}}{{\dfrac{1}{2} + 1}}} \right]$ i.e. $(4, - 2,6)$

16. If the points $A(1,0, - 6) = B( - 3,P,q)$ and $C( - 5,9,6)$are collinear, find the values of ${\mathbf{P}}$and ${\mathbf{q}}$

Ans: Given points 

$A(1,0, - 6) = B( - 3,P,q)$ and $C( - 5,9,6)$ are collinear

Let point $B$ divide $AC$ in the ratio K:1

$\therefore $  co-ordinates of point $A\left( {\dfrac{{1 - 5K}}{{K + 1}} \cdot \dfrac{{0 + 9K}}{{K + 1}},\dfrac{{ - 6 + 6K}}{{K + 1}}} \right)$

$B( - 3,P,q)$

$\dfrac{{1 - 5K}}{{K + 1}} =  - 3$

$1 - 5K =  - 3K - 3$

$ - 2K =  - 4$

$K = \dfrac{{ - 4}}{{ - 2}}$

$K = 2$

$\therefore $ The value of ${\text{P}}$ and ${\text{q}}$ are 6 and 2.

17. Three consecutive vertices of a parallelogram $PQRS$ are $P(3, - 1,2),Q(1,2, - 4)$ and $R( - 1,1,2)$. Find fourth vertex $S$.

Ans: Given vertices of $Paralle\log ramPQRS$

$P(3, - 1,2),Q(1,2, - 4),R( - 1,1,2)$

Suppose co-ordinates of fourth vertex $S(x,y,z)$

Mid-point of $PR\left( {\dfrac{{3 - 1}}{2},\dfrac{{ - 1 + 1}}{2},\dfrac{{2 + 2}}{2}} \right)$

$ = (1,0,2)$

Mid-point of $QS\left( {\dfrac{{x + 1}}{2},\dfrac{{y + 2}}{2},\dfrac{{ - 4 + z}}{2}} \right)$

Mid-point of $PR$ = mid-point of $QS$

$\dfrac{{x + 1}}{2} = 1 \Rightarrow x = 1$

$\dfrac{{y + 2}}{2} = 0 \Rightarrow y =  - 2$

$\dfrac{{ - 4 + z}}{2} = 2 \Rightarrow z = 8$

Co-ordinates of point $S(1, - 2,8)$.

18. If $P$ and $Q$be the points $(3.4,5)$ and $( - 1,3,7)$ respectively. Find the eq. of the set points $A$ such that $A{P^2} + A{Q^2} = {K^2}$ where ${\mathbf{K}}$ is a constant.

Ans: Let co-ordinates of point P be$(x,y,z)$

$A{P^2} = {(x - 3)^2} + {(y - 4)^2} + {(z - 5)^2}$

$ = {x^2} - 6x + 9 + {y^2} - 8y + 16 + {z^2} - 10z + 25$

$ = {x^2} + {y^2} + {z^2} - 6x - 8y - 10z + 50$

$A{Q^2} = {(x + 1)^2} + {(y - 3)^2} + {(z - 7)^2}$

$ = {x^2} + 2x + 1 + {y^2} - 6y + 9 + {z^2} - 14 + 49$

$ = {x^2} + {y^2} + {z^2} + 2x - 6y - 14z + 59$

$A{P^2} + A{Q^2} = {K^2}$

$2\left( {{x^2} + {y^2} + {z^2}} \right) - 4x - 14y - 24z + 109 = {K^2}$

${x^2} + {y^2} + {z^2} - 2x - 7y - 12z = \dfrac{{{K^2} - 109}}{2}$

6 Marks Questions

1. Prove that the lines joining the vertices of a tetrahedron to the centroids of the opposite faces are concurrent.

Ans: Let $PQRS$ be tetrahedron such that the coordinates of its vertices are $P\left( {{x_1},{y_1},{z_1}} \right)$, $Q\left( {{x_2},{y_2},{z_2}} \right),R\left( {{x_2},{y_3},{z_3}} \right)$ and $S({x_4},{y_4},{z_4})$.

The coordinates of the centroids of faces $PQR,SPQ,SQR$ and $SRP$respectively.

${G_1}\left[ {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right]$

${G_2}\left[ {\dfrac{{{x_1} + {x_2} + {x_4}}}{3},\dfrac{{{y_1} + {y_2} + {y_4}}}{3} \cdot \dfrac{{{z_1} + {z_2} + {z_4}}}{3}} \right]$

${G_3}\left[ {\dfrac{{{x_2} + {x_3} + {x_4}}}{3},\dfrac{{{y_2} + {y_3} + {y_4}}}{3},\dfrac{{{z_2} + {z_3} + {z_4}}}{3}} \right]$

${G_4}\left[ {\dfrac{{{x_4} + {x_3} + {x_1}}}{3},\dfrac{{{y_4} + {y_3} + {y_1}}}{3} \cdot \dfrac{{{z_4} + {z_3} + {z_1}}}{3}} \right]$

Now, coordinates of point $G$ dividing $S{G_1}$ in the ratio 3: 1are

$\left[ {\dfrac{{1.{x_4} + 3\left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3}} \right)}}{{1 + 3}} = \dfrac{{1.{y_4} + 3\left( {\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)}}{{1 + 3}} = \dfrac{{1 - {z_4} + 3\left( {\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)}}{{1 + 3}}} \right]$

$ = \left[ {\dfrac{{{x_1} + {x_2} + {x_3} + {x_4}}}{4},\dfrac{{{y_1} + {y_2} + {y_3} + {y_4}}}{4},\dfrac{{{z_1} + {z_2} + {z_3} + {z_4}}}{4}} \right]$

Similarly the point dividing $R{G_2},P{G_3},Q{G_4}$ and $S{G_1}$ in the ratio 3:1 has the same coordinates.

Hence the point $G\left[ {\dfrac{{{x_1} + {x_2} + {x_3} + {x_4}}}{4},\dfrac{{{y_1} + {y_2} + {y_3} + {y_4}}}{4},\dfrac{{{z_1} + {z_2} + {z_3} + {z_4}}}{4}} \right]$ is common to

$S{G_1}$, $R{G_2},P{G_3}$ and $Q{G_4}$

Hence, they are concurrent.

2. The midpoints of the sides of a triangle are $(1,5, - 1),(0,4, - 2)$ and $(2,3,4)$. Find its vertices.

Ans: Let the vertices of triangle be

$A\left(x_{1}, y_{1}, z_{1}\right), B\left(x_{2}, y_{2}, z_{2}\right)$ and $C\left(x_{3}, y_{3}, z_{3}\right)$

Mid-point of $A C$ is $E$

$\therefore \quad\left(\dfrac{x_{1}+x_{3}}{2}, \dfrac{y_{1}+y_{3}}{2}, \dfrac{z_{1}+z_{3}}{2}\right) \equiv(0,4,-2)$

So, $C\left(x_{3}, y_{3}, z_{3}\right) \equiv C\left(-x_{1}, 8-y_{1},-4-z_{1}\right)$

(i)

Mid-point of $A B$ is $F$

$\therefore \quad\left(\dfrac{x_{1}+x_{2}}{2}, \dfrac{y_{1}+y_{2}}{2}, \dfrac{z_{1}+z_{2}}{2}\right) \equiv(2,3,4)$

So, $B\left(x_{2}, y_{2}, z_{2}\right) \equiv B\left(4-x_{1}, 6-y_{1}, 8-z_{1}\right)$

(ii) Mid-point of BC is

 $\therefore \quad \dfrac{-x_{1}+4-x_{1}}{2} =1,$$\dfrac{8-y_{1}+6-y_{1}}{2}=5$

 $\dfrac{-4-z_{1}+8-z_{1}}{2}=-1$

 $\Rightarrow \quad x_{1}=1, y_{1}=2 \text { and } z_{1}=3$

 $\therefore \quad A \equiv(1,2,3)$

 So, $B \equiv(3,4,5) \quad$ [Using (ii)]

 and $C \equiv(-1,6,-7) \quad$ [Using (i)]

 Centroid, $G \equiv\left(\dfrac{1+3-1}{3}, \dfrac{2+4+6}{3}, \dfrac{3+5-7}{3}\right)$

 $\equiv\left(1,4, \dfrac{1}{3}\right)$

3. Let $P\left( {{x_1} \cdot {y_1},{z_1}} \right)$ and $Q\left( {{x_2} \cdot {y_2},{z_2}} \right)$ be two points in space find co- ordinate of point $R$which divides$P$and $Q$ in the ratio ${m_1}:{m_2}$ by geometrically.

Ans: Let co-ordinate of Point $R$ be $(x,y,z)$ which divide line segment joining the point  $P$and $Q$ in the ratio ${m_1}:{m_2}$

Clearly , $\vartriangle PR{L^\prime }~\Delta QR{M^\prime }\quad [By - AA$similarity]

$\therefore \dfrac{{P{L^\prime}}}{{M{Q^\prime }}} = \dfrac{{PR}}{{RQ}}$

$ \Rightarrow \dfrac{{L{L^\prime } - LP}}{{MQ - M{M^\prime }}} = \dfrac{{{m_1}}}{{{m_2}}}$

$ \Rightarrow \dfrac{{NR - LP}}{{MQ - NR}} = \dfrac{{{m_1}}}{{{m_2}}}$

${\because L{L^\prime } = NR}$

${{\text{ and }}M{M^\prime } = NR}$

$ \Rightarrow \dfrac{{z - {z_1}}}{{{z_2} - z}} = \dfrac{{{m_1}}}{{{m_2}}}$

$ \Rightarrow z = \dfrac{{{m_1}{z_2} + {m_2}{z_1}}}{{{m_1} + {m_2}}}$

Similarly , we get

$y = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}$

4. Show that the plane $px + qy + rz + s = 0$ divides the line joining the points $\left( {{x_1},{y_1},{z_1}} \right)$and $\left( {{x_2},{y_2},{z_2}} \right)$ in the ratio $\dfrac{{p{x_1} + q{y_1} + r{z_1} + s}}{{p{x_2} + q{y_2} + r{z_2} + s}}$.

Ans: Let the plane $px + qy + rz + s = 0$ divide the line joining the points $\left( {{x_1},{y_1},{z_1}} \right)$ and$\left( {{x_2},{y_2},{z_2}} \right)$ in the ratio $\lambda  = 1$.

$\therefore x = \dfrac{{\widehat {2{x_2}} + {x_1}}}{{\lambda  + 1}} = y = \dfrac{{\lambda {y_2} + {y_1}}}{{\lambda  + 1}} = z = \dfrac{{\lambda {z_2} + {z_1}}}{{\lambda  + 1}}$

$\because $ Plane $px + qy + rz + s = 0$Passing through $\left( {{x_0}y,z} \right)$

$\therefore p\dfrac{{\left( {\lambda {x_2} + {x_1}} \right)}}{{\lambda  + 1}} + q\dfrac{{\left( {\lambda {y_2} + {y_1}} \right)}}{{\lambda  + 1}} + r\dfrac{{\left( {\lambda {z_2} + {z_1}} \right)}}{{2 + 1}} + s = 0$

$p\left( {\lambda {x_2} + {x_1}} \right) + q\left( {\lambda {y_2} + {y_1}} \right) + r\left( {\lambda {z_2} + {z_1}} \right) + s(\lambda  + 1) = 0$

$\lambda \left( {p{x_2} + q{y_2} + r{z_2} + s} \right) + \left( {p{x_1} + q{y_1} + r{z_1} + s} \right) = 0$

$\lambda  =  - \dfrac{{\left( {p{x_1} + q{y_1} + r{z_1} + s} \right)}}{{\left( {p{x_2} + q{y_2} + r{z_2} + s} \right)}}$

Hence Proved.

5.Prove that the points$0(0,0,0),P(2,0,0),Q(1,\sqrt 3 ,0)$, and $R\left( {1,\dfrac{1}{{\sqrt 3 }},\dfrac{{2\sqrt 2 }}{{\sqrt 3 }}} \right)$ are

The vertices of a regular tetrahedron.

Ans: To prove $O,P,Q,R$ are vertices of regular tetrahedron.

${{\text{ We have to show that }}}$

${|OP| = |OQ| = |OR| = |PQ| = |QR| = |RP|}$

${|OP| = \sqrt {{{(0 - 2)}^2} + {0^2} + {0^2}}  = 2{\text{ unit }}}$

${|{\text{OQ}}| = \sqrt {{{(0 - 1)}^2} + {{(0 - \sqrt 3 )}^2} + {0^2}}  = \sqrt {1 + 3}  = \sqrt 4  = 2{\text{ unit }}}$

${|OR| = \sqrt {{{(0 - 1)}^2} + \left( {0 - \dfrac{1}{{\sqrt 3 }}} \right) + {{\left( {0 - \dfrac{{2\sqrt 2 }}{3}} \right)}^2}} }$ 

${ = \sqrt {1 + \dfrac{1}{3} + \dfrac{8}{3}} }$

${ = \sqrt {\dfrac{{12}}{3}}  = \sqrt 4  = 2{\text{ unit }}}$

${|AB| = \sqrt {{{(2 - 1)}^2} + {{(0 - \sqrt 3 )}^2} + {{(10 - 0)}^2}}  = \sqrt {1 + 3 + 0} }$ 

${ = \sqrt 4  = 2{\text{ unit }}}$ 

${|BC| = \sqrt {{{(1 - 1)}^2} + {{\left( {\sqrt 3  - \dfrac{1}{{\sqrt 3 }}} \right)}^2} + {{\left( {0 - \dfrac{{2\sqrt 2 }}{{\sqrt 3 }}} \right)}^2}} }$

${ = \sqrt {0 + {{\left( {\dfrac{2}{{\sqrt 3 }}} \right)}^2} + \dfrac{8}{3}} }$ 

$ = \sqrt {\dfrac{{12}}{3}}  = 2{\text{unit}}$

$|{\text{CA}}| = \sqrt {{{(1 - 2)}^2} + {{\left( {\dfrac{1}{{\sqrt 3 }} - 0} \right)}^2} + {{\left( {\dfrac{{2\sqrt 2 }}{{\sqrt 3 }} - 0} \right)}^2}} $

$ = \sqrt {1 + \dfrac{1}{3} + \dfrac{8}{3}} $

$ = \sqrt {\dfrac{{12}}{3}}  = 2{\text{unit}}$

$\therefore |{\text{AB}}| = |{\text{BC}}| = |{\text{CA}}| = |{\text{OA}}| = |{\text{OB}}| = |{\text{OC}}| = 2$ unit

${\text{O,P,Q,R}}$ are vertices of a regular tetrahedron.

6. If ${\text{P}}$ and  ${\text{Q}}$ are the points $( - 2,2,3)$ and $( - 1,4, - 3)$ respectively, then find the locus of

${\text{A}}$ such that $3|AP| = 2|\;AQ|$.

Ans: The Given points $P( - 2,2,3)$ and $Q( - 1,4, - 3)$

Suppose co-ordinates of point $A(x,y,z)$

$|AP| = \sqrt {{{(x + 2)}^2} + {{(y - 2)}^2} + {{(2 - 3)}^2}} $

$|{\text{AP}}| = \sqrt {{x^2} + {y^2} + {z^2} + 4x - 4y - 6z + 17} $

$|AQ| = \sqrt {{{(x + 1)}^2} + {{(y - 4)}^2} + {{(z + 3)}^2}} $

$|AQ| = \sqrt {{x^2} + {y^2} + {z^2} + 2x - 8y + 6z + 26} $

$9A{P^2} = 4\;A{Q^2}$

$9\left( {{x^2} + {y^2} + {z^2} + 4x - 4y - 6z + 17} \right) = 4\left( {{x^2} + {y^2} + {z^2} + 2x - 8y + 6z + 26} \right)$

\[\left( {5{x^2} + 5{y^2} + 5{z^2} + 28x - 4y - 30z + 49 = 0} \right)\]

Benefits of Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry - Important Questions

• Helps in understanding the basics of 3D geometry, like coordinates, distance, and section formulas.

• Builds a foundation for advanced topics in higher classes and competitive exams.

• Improves problem-solving and analytical thinking skills.

• Provides practice with a variety of questions to prepare effectively for exams.

• Helps students get familiar with the type of questions asked in CBSE exams.

• Step-by-step solutions make it easier to understand and clear doubts.

• Saves time by focusing on the most important and frequently asked questions.

• Boosts confidence in understanding 3D geometry problems.

Important Study Materials for Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry

CBSE Class 11 Maths Chapter-wise Important Questions

CBSE Class 11 Maths Chapter-wise Important Questions and Answers cover topics from all 14 chapters, helping students prepare thoroughly by focusing on key topics for easier revision.

Additional Study Materials for Class 11 Maths