Important Questions for CBSE Class 11 Physics Chapter 10 - Thermal Properties of Matter

2 Marks Questions

1. A copper block of mass $2.5\;{\text{kg}}$ is heated in a furnace to a temperature of ${{{500}^{0}} }{\text{C}}$ and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper $ = 0.39{\text{J}}{{\text{g}}^{ - 1}}\;{{\text{K}}^{ - 1}}$; heat of fusion of water $ = 335{\text{J}}{{\text{g}}^{ - 1}}$

Ans: The copper block's mass, $m = 2.5\;{\text{kg}} = 2500\;{\text{g}}$

The temperature of the copper block has risen, $\Delta \theta  = {{{500}^{0}} }{\text{C}}$

Copper's specific heat \[_uC = 0.39{\text{J}}{{\text{g}}^{ - 1}}{{\text{C}}^{ - 1}}\]

The heat of water fusion, $L = 335{\text{J}}{{\text{g}}^{ - 1}}$

The greatest amount of heat that a copper block may lose in a given amount of time, $= mC\Delta \theta $

$ = 2500 \times 0.39 \times 500$

$ = 487500\;{\text{J}}$

Let ${m_1}g$ be the amount of ice that melts when the copper block is put on the ice block,

The heat that the melting ice has acquired, $= {m_1}L$

$\therefore {m_1} = \dfrac{Q}{L} = \dfrac{{487500}}{{335}} = 1455.22\;{\text{g}}$

As a result, the total amount of ice that can melt is $1.45\,{\text{kg}}$.

2. A 'thermocol' icebox is a cheap and efficient method for storing small quantities of cooked food in summer in particular. A cubical icebox of side $30\;{\text{cm}}$ has a thickness of $5.0\;{\text{cm}}$. If $4.0\;{\text{kg}}$ of ice is put in the box, estimate the amount of ice remaining after $6\;{\text{h}}$.

The outside temperature is ${{{45}^{0}} }{\text{C}}$, and co-efficient of thermal conductivity of thecmacole is $0.01{\text{J}}{{\text{s}}^{ - 1}}\;{{\text{m}}^{ - 1}}\;{{\text{K}}^{ - 1}}$. [Heat of fusion of water $ = 335 \times {10^3}\;{\text{J}}\;{\text{k}}{{\text{g}}^{ - 1}}{\text{l}}$

Ans: The provided cubical ice box's side, $s = 30\;{\text{cm}} = 0.3\;{\text{m}}$

The ice box's thickness, $l = 5.0\;{\text{cm}} = 0.05\;{\text{m}}$

In the ice because of ice kept, $m = 4\;{\text{kg}}$

Time gap, $t = 6\;{\text{h}} = 6 \times 60 \times 60\;{\text{s}}$

the temperature outside, $T = {{{45}^{0}} }{\text{C}}$

Thermacele's heat conductivity coefficient, $K = 0.01{\text{J}}{{\text{s}}^{ - 1}}\;{{\text{m}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

The heat of water fusion, $L = 335 \times {10^3}\;{\text{J}}\;{\text{k}}{{\text{g}}^{ - 1}}$

Let's call $m$ be the total amount of ice that melts in $6\;{\text{h}}$.

The quantity of heat lost by the meal is calculated as follows:

$\theta  = \dfrac{{KA(T - 0)t}}{l}$

Where, In such case, the surface area

$A = {\text{ Surface area of the }}b0x = 6{s^2} = 6 \times {(0.3)^2} = 0.54\;{{\text{m}}^3}$

$\theta  = \dfrac{{0.01 \times 0.54 \times (45) \times 6 \times 60 \times 60}}{{0.05}} = 104976J$

But $\theta  = mL$

$\therefore {m^\prime } = \dfrac{\theta }{L}$

$ = \dfrac{{104976}}{{335 \times {{10}^3}}} = 0.313\;{\text{kg}}$

Mass of ice left $ = 4 - 0.313 = 3.687\;{\text{kg}}$

As a result, the amount of ice left after is. $6\;{\text{h}}$ is $3.687\;{\text{kg}}$.

3 Marks Questions

1. The triple points of neon and carbon dioxide are $24.57\;{\text{K}}$ and $216.55\;{\text{K}}$ respectively. Express these temperatures on the Celsius and Fahrenheit scales. 

Ans: The following is a relation between the Kelvin and Celsius scales:

$${T_c} = {T_k} - 273.15 \ldots {\text{ (j) }}$$

The temperature scales in Celsius and Fahrenheit are linked in the following way:

$${T_F} = \dfrac{9}{5}{T_c} + 32 \ldots $$

If you want to use neon, you need use the following formula.

${{T_{\text{k}}} = 24.57\;{\text{K}}} $

${\therefore {T_{\text{c}}} = 24.57 - 273.15 =  - 248.58{\text{C}}} $ 

${{T_F} = \dfrac{9}{5}{T_c} + 32}$

$={\dfrac{9}{5}( - 248.58) + 32}$

${ = {{415.44}^2}\;{\text{F}}}$ 

In case of carbon dioxide:

${{T_{\text{K}}} = 216.55\;{\text{K}}} $

${\therefore {T_c} = 216.55 - 273.15 =  - {{56.60}^{0}}{\text{C}}}$

${{T_F} = \dfrac{9}{5}\left( {{T_6}} \right) + 32}$

${ = \dfrac{9}{5}( - 56.60) + 32} $

${ =  - 69.88{\text{C}}}$ 

2. Two absolute scales A and B have triple points of water defined to be $200\;{\text{A}}$ and $350\;{\text{B}}.$ What is the relation between ${T_A}$ and ${T_B}$ ?

Ans: Water's triple point on the absolute scale $A,{T_1} = 200\;{\text{A}}$

Water's triple point on the absolute scale ${{\text{B}}_2}{T_2} = 350\;{\text{B}}$

Water's triple point on the Kelvin scale, ${T_X} = 273.15\;{\text{K}}$

The temperature $273.15\;{\text{K}}$ on Kelvin scale is equal to $200\;{\text{A}}$ on absolute scale ${\text{A}}$.

${{T_1} = {T_K}} $

${200\;{\text{A}} = 273.15\;{\text{K}}} $

${\therefore A = \dfrac{{273.15}}{{200}}}$

The temperature $273.15\;{\text{K}}$ on Kelvin scale is equal to $350\;{\text{B}}$ on absolute scale ${\text{B}}$.

${{T_2} = {T_K}}$

${350\;{\text{B}} = 273.15} $ 

${\therefore B = \dfrac{{273.15}}{{350}}}$ 

On a scale $A,{T_A}$ is triple point of water.

On a scale ${\text{B,}}{T_B}$ is triple point of water.

${\therefore  = \dfrac{{273.15}}{{200}} \times {T_A} = \dfrac{{273.15}}{{350}} \times {{\bar T}_B}}$ 

 $ {{T_A} = \dfrac{{200}}{{350}}{T_B}}$ 

Hence, the ratio ${T_A}:{T_B}$ is given as 4.7.

3. A steel tape $1\;{\text{m}}$ long is correctly calibrated for a temperature of ${27.{0}^{0} }{\text{C}}$. The length of a steel rod measured by this tape is found to be $63.0\;{\text{cm}}$ on a hot day when the temperature is ${45.{0}^{0} }{\text{C}}$. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is ${27.{0}^{0} }{\text{C}}\quad $ ? Coefficient of linear expansion of steel $ = 1.20 \times {10^{ - 6}}\;{{\text{K}}^{ - 1}}$

Ans: Temperature-dependent length of steel tape $T = {{27}^{0} }{\text{C}},l = 1\;{\text{m}} = 100\;{\text{cm}}$ At temperature ${T_1} = {{{45}^{0}} }{\text{C}}$, the length of the steel rod, ${l_1} = 63\;{\text{cm}}$

Coefficient of linear expansion of steel, $a = 1.20 \times {10^{ - 5}}{{\mathbf{K}}^{ - 1}}$

Let, $l$ be the real length of the steel rod and $l$ be the length of the steel tape at ${{{45}^{0}} }{\text{C}}$

${{l^\prime } = l + al\left( {{T_1} - T} \right)}$

${\therefore {l^\prime } = 100 + 1.20 \times {{10}^{ - 5}} \times 100(45 - 27)} $

$  { = 100.0216\;{\text{cm}}} $

Therefore, As a result, the actual length of the steel rod ${{{45}^{0}} }{\text{C}}$ can be computed as follows:

${l_2} = \dfrac{{100.0216}}{{100}} \times 63$

$ = 63.0136\;{\text{cm}}$

As a result, the rod's real length is at

${{{45.0}^{0}}}{\text{C}}$ is $63.0136\;{\text{cm}}$. Its total length at ${{27.0}^{0}}{\text{C}}$ is $63.0\;{\text{cm}}$.

4. A $10\;{\text{kW}}$ drilling machine is used to drill a bore in a small aluminium block of mass $8.0\,{\text{kg}}$. How much is the rise in temperature of the block in 2.5 minutes, assuming $50\% $ of power is used up in heating the machine itself or lost to the surroundings. Specific heat of aluminium $ = 0.91\,{\text{J}}{{\text{g}}^{ - 1}}{{\text{K}}^{ - 1}}$

Ans: Drilling machine's power $P = 10\;{\text{kW}} = 10 \times {10^3}\;{\text{W}}$

The aluminium block's mass, $m = 8.0\;{\text{kg}} = 8 \times {10^3}\;{\text{g}}$

The length of time that the machine is in use, $t = 2.5\;{\text{min}} = 2.5 \times 60 = 150\;{\text{s}}$

Aluminum's specific heat, $c = 0.91{\text{J}}{{\text{g}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

After drilling, the block's temperature rises $ = \delta T$

Drilling machine's total energy $ = {P_t}$

$  { = 10 \times {{10}^3} \times 150}$  

${ = 1.5 \times {{10}^6}\;{\text{J}}} $

Only a $50\% $ portion of the power is usable.

However, it is useful energy $\vartriangle = \dfrac{{50}}{{100}} \times 1.5 \times {10^5} = 7.5 \times {10^5}\;{\text{J}}$

$ {{\text{But}}\Delta = m{c_\Delta }T} $

$  {\therefore A = \dfrac{{\Delta Q}}{{mc}}} $

$  { = \dfrac{{7.5 \times {{10}^5}}}{{8 \times {{10}^3} \times 0.91}}} $

$  { = {{103}^{0} }{\text{C}}} $

As a result, the temperature of the block rises by ${{103}^{0} }{\text{C}}$ in $2.5$ minutes of drilling.

5. In an experiment on the specific heat of a metal, a $0.20\;{\text{kg}}$ block of the metal at ${15{0}^{0} }{\text{C}}$ is dropped in a copper calorimeter (of water equivalent $0.025\;{\text{kg}}$ ) containing $150\;{\text{c}}{{\text{m}}^3}$ of water at ${{27}^{0} }{\text{C}}$. The final temperature is ${{40}^{0} }{\text{C}}$. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal?

Ans: The metallic mass, $m = 0.20\;{\text{kg}} = 200\;{\text{g}}$

The metal's initial temperature, ${T_1} = {15{0}^{0} }{\text{C}}$

The metal's final temperature, ${T_2} = {{40}^{0} }{\text{C}}$

The mass of a calorimeter is equal to the mass of water, ${m^\prime } = 0.025\;{\text{kg}} = 25\;{\text{g}}$

Volume of water, $V = 150\;{\text{c}}{{\text{m}}^3}$

Water mass $^{(M)}$ at given temperature $T = {{27}^{0} }{\text{C}}$ :

$150 \times 1 = 150\;{\text{g}}$

The temperature of the metal has dropped:

$$\Delta T = {T_1} - {T_2} = 150 - 40 = {11{0}^{0} }{\text{C}}$$

Water's specific heat, ${C_w} = 4.186\;{\text{J}}/{\text{g}}{/^1}\;{\text{K}}$

Metal's specific heat, $ = C$

Metal dissipates heat, $\theta  = mC\Delta T \ldots $ (i)

The temperature of the water and the calorimeter system is rising:

$\Delta {T^{\prime \prime }} = 40 - 27 = {{13}^{0} }{\text{C}}$

Heat obtained by the water and calorimeter system:

$\Delta {\theta ^{\prime \prime }} = {m_1}{C_{\text{v}}}\Delta {T^\prime }$

$ = \left( {M + {m^\prime }} \right){C_u}\Delta {T^\prime } \ldots {\text{ (ii) }}$

Heat lost by the metal = Heat gained by the water and colorimeter system.

$mC\Delta T = \left( {M + {m^\prime }} \right){C_ \vee }\Delta T$

$  {200 \times C \times 110 = (150 + 25) \times 4.186 \times 13} $

$  {\therefore C = \dfrac{{175 \times 4.186 \times 13}}{{110 \times 200}} = 0.43{\text{J}}{{\text{g}}^{ - 1}}{K^{ - 1}}} $

If heat is lost to the environment, the value will of $C$ will be lower than the real value.

4 Marks Questions

1. The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law:

$R = {R_0}\left[ {1 + \alpha \left( {T - {T_e}} \right)} \right]$

The resistance is $101.6\Omega $ at the triple-point of water $273.16\;{\text{K}}$, and $165.5\Omega $ at the normal melting point of lead $(600.5\;{\text{K}}).$ What is the temperature when the resistance is $123.4\Omega ?$

Ans: It is assumed that:

$R = R = {R_0}\left[ {1 + \alpha \left( {T - {T_\theta }} \right)} \right] \ldots (i)$

Where,

${R_0}$ and ${T_0}$ are the starting resistance and temperature respectively $R$ and $T$ are the ultimate resistance and temperature, respectively a is a constant

When water reaches its triple point, ${T_0} = 273.15\;{\text{K}}$

Lead resistance, ${R_0} = 101.6\Omega $

When these values are substituted in equation (i), we get:

$  {R = {R_0}\left[ {1 + a\left( {T - {T_0}} \right)} \right]} $

$  {165.5 = 101.6[1 + a(600.5 - 273.15)]} $

$  {1.629 = 1 + a(327.35)} $  

${\therefore a = \dfrac{{0.629}}{{327.35}} = 1.92 \times {{10}^{ - 3}}\;{{\text{K}}^{ - 1}}} $

For resistance, ${R_1} = 123.4\Omega $

$R = {R_0}\left[ {1 + a\left( {T - {T_0}} \right)} \right]$

Where, ${\text{T}}$ is the temperature when the resistance of lead is calculated $123.4\Omega $

$  {123.4 = 101.6\left[ {1 + 1.92 \times {{10}^{ - 3}}(T - 273.15)} \right]} $

$  {1.214 = 1 + 1.92 \times {{10}^{ - 3}}(T - 273.15)} $

$  {\dfrac{{0.214}}{{1.92 \times {{10}^{ - 1}}}} = T - 273.15} $

$\therefore T = 384.61\;{\text{K}}$

2. A large steel wheel is to be fitted on to a shaft of the same material. At ${{27}^{0} }{\text{C}}$, the outer diameter of the shaft is $8.70\;{\text{cm}}$ and the diameter of the central hole in the wheel is $8.69\;{\text{cm}}$. The shaft is cooled using 'dry ice'. At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range: ${\alpha _{{\text{stel }}}} = 1.20 \times {10^{ - 5}}\;{{\text{K}}^{ - 1}}$

Ans: The given temperature, $T = {{27}^{0} }{\text{C}}$ In Kelvin, the given temperature is expressed as:

$27 + 273 = 300\;{\text{K}}$

The steel shaft's outside diameter at $T,{d_1} = 8.70\;{\text{cm}}$ 

The centre hole in the whed has a diameter of $T,{d_2} = 8.69\;{\text{cm}}$

Steel linear expansion coefficient, ${a_{{\text{tedl }}}} = 1.20 \times {10^{ - 5}}{K^{ - 1}}$

The temperature of the shaft drops when it is cocled with dry ice. ${T_1}$

If the diameter of the wheel changes, it will slip on the shaft, $\Delta {\text{d}} = 8.69 - 8.70$$ =  - 0.01\;{\text{cm}}$

Temperature ${T_1}$, can be determined from the relation:

$  {\Delta d = d_1^d{u_{{\text{thal }}}}\left( {{T_1} - T} \right)} $

$  {0.01 = 8.70 \times 1.20 \times {{10}^{ - 5}}\left( {{T_1} - 300} \right)} $

$  {\left( {{T_1} - 300} \right) = 95.78}$

$  {\therefore {T_1} = 204.21\;{\text{K}}} $

$  { = 204.21 - 273.16} $

$ =  - {{68.95}^{0} }{\text{C}}$

Therefore, when the shaft temperature is $ - {{69}^{0}}{\text{C}}$ the wheel will slip on.

3. Given below are observations on molar specific heats at room temperature of some common gases.

The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is $2.92{\text{cal}}/{\text{molK}}$. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine?

Ans: The gases indicated in the table are diatomic in nature. They have other degrees of freedom (modes of motion) in addition to translational degrees of freedom. Heat must be supplied to raise the temperature of these gases. The average energy of all modes of motion is increased as a result of this. As a result, diatomic gases have a higher molar specific heat than monatomic gases.

If just rotational motion is taken into account, the molar specific heat of a diatomic is gas $ = \dfrac{5}{2}R$

= $\dfrac{5}{2} \times 1.98 = 4.95{\text{calmo}}{{\text{l}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

All of the observations in the table agree with, the exception of chlorine $\left( {\dfrac{5}{2}R} \right)$. This is because, in addition to rotational and translational modes of motion, chlorine exhibits vibrational modes of motion at ambient temperature.

4. The coefficient of volume expansion of glycerin is $49 \times {10^{ - 5}}\;{{\text{K}}^{ - 1}}.$ What is the fractional change in its density for a 30 "C rise in temperature?

Ans: Glycerin volume expansion coefficient, ${\alpha _\gamma } = 49 \times {10^{ - 5}}\;{{\text{K}}^{ - 1}}$

Temperature rises, $\Delta T = {3{0}^{0} }$

Its volume has changed by a fraction $ = \dfrac{{\Delta V}}{V}$

This variation is linked to temperature changes as follows:

$  {\dfrac{{\Delta V}}{V} = {a_{\text{r}}}\Delta T}$

$  {{V_{{T_2}}} - {V_{{T_1}}} = {V_{{T_1}}}{a_1}\Delta T} $ 

$  {\dfrac{m}{{{\rho _{{T_2}}}}} - \dfrac{m}{{{\rho _{{T_1}}}}} = \dfrac{m}{{{\rho _{{T_1}}}}}{a_v}\Delta T} $

Where,

$m = $ Glycerine mass

${\rho _T} = $ Density at initial ${T_1}$

${\rho _{{T_2}}} = $ Density at final ${T_2}$

$\dfrac{{{\rho _{{T_1}}} - {\rho _{{T_2}}}}}{{{\rho _{{T_2}}}}}{a_i}\Delta T$

Where,

$\dfrac{{{\rho _{{T_1}}} - {\rho _{{T_2}}}}}{{{\rho _{{T_2}}}}} = {\text{ Density change expressed as a fraction }}$

$\therefore $ The density of glycerin changes fractionally $ = 49 \times {10^{ - 5}} \times 30 = 1.47 \times {10^{ - 2}}$

5 Marks Questions

1. Answer the following:

(a) The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale)?

(b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number ${{0}^{0} }{\text{C}}$ and ${10{0}^{0} }{\text{C}}$ respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number $273.16\;{\text{K}}.$ What is the other fixed point on this (Kelvin) scale?

(c) The absolute temperature (Kelvin scale) $T$ is related to the temperature $t\,{\text{c}}$ on the Celsius scale by ${t_{\text{c}}} = T - 273.15$

Why do we have 273.15 in this relation, and not 273.16 ?

(d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale?

Ans:

(a) Water's triple point has a one-of-a-kind value of 273.16 K. The triple point of water is always present at specific volume and pressure levels $273.16\;{\text{K}}$. Because the melting point of ice and the boiling point of water are dependent on pressure and temperature, these points do not have specific values.

(b) On the Kelvin absolute scale, the absolute zero or $0\;{\text{K}}$ is the other fixed point.

(c) The temperature is the water's triple point $273.16\;{\text{K}}$ It is not the ice melting point.Ice melts at a temperature ${{0}^{0} }{\text{C}}$ on Celsius. On the Kelvin scale, it corresponds to the value $273.15\;{\text{K}}$

As a result, absolute temperature (Kelvin scale) $T$, and temperature t c on the Celsius scale are linked as follows:

${t_{\text{c}}} = T - 273.15$

(d) Let,$T\;{\text{F}}$ be the Fahrenheit scale temperature and ${T_K}$ be the absolute scale temperature. Both temperatures can be correlated as follows:

$\dfrac{{{T_F} - 32}}{{180}} = \dfrac{{{T_K} - 273.15}}{{100}}$

Let, ${T_{F1}}$ be the Fahrenheit scale temperature and ${T_{K1}}$ be the absolute scale temperature. Both temperatures can be correlated as follows:

$\dfrac{{{T_{F1}} - 32}}{{180}} = \dfrac{{{T_{K1}} - 273.15}}{{100}}$

It is assumed that:

${T_{K1}} - {T_K} = 1K$

When we subtract equation (i) from equation (ii), we obtain the following:

$  {\dfrac{{{T_{F1}} - {T_F}}}{{180}} = \dfrac{{{T_{X1}} - {T_E}}}{{100}} = \dfrac{1}{{100}}} $ 

$  {{T_{F1}} - {T_F} = \dfrac{{1 \times 180}}{{100}} = \dfrac{9}{5}} $

2. Two ideal gas thermometers A and Buse oxygen and hydrogen respectively. The following observations are made:

(a) What is the absolute temperature of normal melting point of sulphur as read by thermometers A and B?

(b) What do you think is the reason behind the slight difference in answers of thermometers ${\text{A}}$ and ${\text{B}}$? (The thermometers are not faulty). What further procedure is needed in the experiment to reduce the discrepancy between the two readings?

Ans: (a) Water's triple point $T = 273.16\;{\text{K}}$

Pressure in the thermometer at this temperature, ${\text{A}},{P_A} = 1.250 \times {10^5}\;{\text{Pa}}$

Let, the usual melting point of sulphur be the ${T_1}$.

The pressure in the thermometer at this temperature is

${\text{A}},{P_B} = 1.797 \times {10^{6{\text{E}}}}{\text{Pa}}$

We have the following relation, according to Charles' law:

$  {\dfrac{{{P_A}}}{T} = \dfrac{{{P_1}}}{{{T_1}}}} $

$  {\therefore {T_1} = \dfrac{{{P_1}T}}{{{P_A}}} = \dfrac{{1.797 \times {{10}^5} \times 273.16}}{{1.250 \times {{10}^3}}}}$

$ { = 392.69\;{\text{K}}} $

As a result, the absolute temperature of sulphur's typical melting point as measured by a thermometer A is $392.69\;{\text{K}}$.

At triple point $273.16\;{\text{K}}$, the pressure in thermometer ${\text{B}}$, ${P_{\text{B}}} = 0.200 \times {10^5}\;{\text{Pa}}$

At temperature ${T_1}$, the pressure in thermometer ${\text{B}},{P_2} = 0.287 \times {10^3}\;{\text{Pa}}$

We can write the relation as follows, according to Charles' law:

$  {\dfrac{{{P_B}}}{T} = \dfrac{{{P_1}}}{{{T_1}}}}$

$  {\dfrac{{0.200 \times {{10}^5}}}{{273.16}} = \dfrac{{0.287 \times {{10}^5}}}{{{T_1}}}} $

$  {\therefore {T_1} = \dfrac{{0.287 \times {{10}^5}}}{{0.200 \times {{10}^5}}} \times 273.16 = 391.98K} $

As a result, the absolute temperature of sulphur's typical melting point, measured using a thermometer, ${\text{B}}$ is $391.98\;{\text{K}}$.

(b) The oxygen and hydrogen gas included in thermometers A and B respectively are not perfect ideal gases. As a result, the readings of thermometers and are somewhat different. A and B.

The experiment should be carried out at low pressure circumstances to decrease the disparity between the two measurements. These gases act like perfect ideal gases at low pressure.

3. A hole is drilled in a copper sheet. The diameter of the hole is $4.24\;{\text{cm}}$ at${27.{0}^{0} }{\text{C}}.$ What is the change in the diameter of the hole when the sheet is heated to ${2{27}^{0} }{\text{C}}$ ? Coefficient of linear expansion of copper $ = 1.70 \times {10^{ - 6}}{{\text{K}}^{ - 1}}$

Ans: Temperature at initial, ${T_1} = {27.{0}^{0} }{\text{C}}$

The hole's diameter at $_2{T_1},{d_1} = 4.24\;{\text{cm}}$

Final temperature, ${T_2} = {2{27}^{0} }{\text{C}}$

The hole's diameter at, ${T_2} = {d_2}$

Copper linear expansion coefficient, ${\alpha _{Cu}} = 1.70 \times {10^{ - 5}}\;{{\text{K}}^{ - 1}}$

We have the following relationship for the co-efficient of superficial expansion $\beta $ and change in temperature, $\Delta T$

$  {\dfrac{{{\text{ Change in area }}(\Delta A)}}{{{\text{ Original area }}(A)}} = {\beta _\Delta }T}$

$  {\dfrac{{\left( {\pi \dfrac{{d_2^2}}{4} - \pi \dfrac{{d_1^2}}{4}} \right)}}{{\left( {\pi \dfrac{{d_1^2}}{4}} \right)}} = \dfrac{{\Delta A}}{A}} $

$  {\therefore \dfrac{{\Delta A}}{A} = \dfrac{{d_2^2 - d_1^2}}{{d_1^2}}} $

$  {{\text{ But }}\beta  = 2a}$

$  {\therefore \dfrac{{d_2^2 - d_1^2}}{{d_1^2}} = 2{a_\Delta }T} $ 

$  {\dfrac{{d_2^2}}{{d_1^2}} - 1 = 2a\left( {{T_2} - {T_1}} \right)} $

$  {\dfrac{{d_2^2}}{{d{{(4.24)}^2}}} = 2 \times 1.7 \times {{10}^{ - 5}}(227 - 27) + 1} $

$  {d_2^2 = 17.98 \times 1.0068 = 18.1} $

$  {\therefore {d_2} = 4.2544\;{\text{cm}}} $

As a result, the diameter grows by. $1.44 \times {10^{ - 2}}\;{\text{cm}}$

4. A brass wire $1.8\;{\text{m}}$ long at ${{27}^{0} }{\text{C}}$ is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of ${{39}^{0} }{\text{C}}$, what is the tension developed in the wire, if its diameter is $2.0\;{\text{mm}}$ ? Co-efficient of linear expansion of brass $ = 2.0 \times {10^{ - 6}}\;{{\text{K}}^{ - 1}}$; Young's modulus of brass $ = 0.91 \times {10^{11}}\;{\text{Pa}}$

Ans: Temperature at initial, ${T_1} = {{27}^{0} }{\text{C}}$

Brass wire length at ${T_1},l = 1.8\;{\text{m}}$

Final temperature, ${T_2} =  - {{39}^{0} }{\text{C}}$

The wire's diameter is, $d = 2.0\;{\text{mm}} = 2 \times {10^{ - 3}}\;{\text{m}}$

Tension developed in the wire $ = F$

Brass linear expansion coefficient, $a = 2.0 \times {10^{ - 5}}\;{{\text{K}}^{ - 1}}$

Brass Young's modulus,

$Y = 0.91 \times {10^{11}}Pa$

Young's modulus can be calculated using the following formula:

$Y = \dfrac{{{\text{ Stress }}}}{{{\text{ Strain }}}} = \dfrac{{\dfrac{F}{A}}}{{\dfrac{{\Delta L}}{L}}}$

$L = \dfrac{{F \times L}}{{A \times Y}}$

Where,

$F = $ Tension developed in the wire

$A = $ Area of cross-section of the wire.

$\Delta L = $ Change in the length, given by the relation:

$\Delta L = aL\left( {{T_2} - {T_1}} \right) \ldots {\text{ (ii) }}$

When we combine equations (i) and (ii), we get the following result:

$  {aL\left( {{T_2} - {T_1}} \right) = \dfrac{{FL}}{{\pi {{\left( {\dfrac{d}{2}} \right)}^2} \times Y}}}$

$ {F = a\left( {{T_2} - {T_1}} \right)\pi {{\left( {\dfrac{d}{2}} \right)}^2}}$

$F=2\times 10^{-5}\left ( -39-27 \right )\left (3.14  \right )\left (\frac{2\times 10^{-3}}{2}  \right )^{2}$

$ =  - 3.8 \times {10^2}N$

$= 3.8 \times {10^2}N$ (The minus symbol denotes inward strain.)

As a result, the wire's tension rises $3.8 \times {10^2}\;{\text{N}}$.

5. A brass rod of length $50\;{\text{cm}}$ and diameter $3.0\;{\text{mm}}$ is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at ${{250}^{0} }{\text{C}}$, if the original lengths are at ${{40.0}^{0} }{\text{C}}$ ? Is there a 'thermal stress" developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass $ = 2.0 \times {10^{ - 6}}{{\mathbf{K}}^{ - 1}}$, steel $\left. { = 1.2 \times {{10}^{ - 6}}{{\mathbf{K}}^{ - 1}}} \right)$

Ans: Temperature at initial, ${T_1} = {{40}^{0} }{\text{C}}$ Temperature at final, ${T_2} = {{250}^{0} }{\text{C}}$

Change in temperature, $\Delta T = {T_2} - {T_1} = {21{0}^{0} }{\text{C}}$

Length of the brass rod at, ${T_1},{l_1} = 50\;{\text{cm}}$

Diameter of the brass rod at ${T_1},{d_1} = 3.0\;{\text{mm}}$

Length of the steel rod at, ${T_2},{l_2} = 50\;{\text{cm}}$

Diameter of the steel rod at ${T_2},{d_2} = 3.0\;{\text{mm}}$

Brass linear expansion coefficient ${\alpha _1} = 2.0 \times {10^{ - 6}}{{\mathbf{K}}^{ - 1}}$

Steel linear expansion coefficient, ${\alpha _2} = 1.2 \times {10^{ - 6}}{{\mathbf{K}}^{ - 1}}$

We have the following for brass rod expansion:

$\dfrac{{{\text{ Change in area }}(\Delta A)}}{{{\text{ Original area }}(A)}} = {a_1}\Delta T$

$  {\therefore \Delta {l_1} = 50 \times \left( {2.1 \times {{10}^{ - 5}}} \right) \times 210} $

$  { = 0.2205\;{\text{cm}}} $

For the steel rod's expansion, we have:

$  {\dfrac{{{\text{ Change in area }}(\Delta A)}}{{{\text{ Original area }}(A)}} = {a_2}\Delta T}$ 

$  {\therefore \Delta {l_2} = 50 \times \left( {2.1 \times {{10}^{ - 5}}} \right) \times 210} $

$  { = 0.126\;{\text{cm}}} $

Total change in brass and steel lengths,

$\Delta l = {\Delta _1} + \Delta {l_2}$

$ = 0.2205 + 0.126$

$ = 0.346\;{\text{cm}}$

Total change in the length of the combined, $\operatorname{rod}  = 0.346\;{\text{cm}}$

Because the rod extends freely from both ends, there is no heat tension at the connection.

6.Answer the following questions based on the $P - T$ phase diagram of carbon dioxide:

(a) At what temperature and pressure can the solid, liquid and vapour phases of ${\text{C}}{{\text{O}}_2}$ co-exist in equilibrium?

(b) What is the effect of decrease of pressure on the fusion and boiling point of ${\text{C}}{{\text{O}}_2}?$

(c) What are the critical temperature and pressure for ${\text{C}}{{\text{O}}_2}$ ? What is their significance?

(d) Is $C$ O 2 solid, liquid or gas at 

1. - ${7{0}^{0} }{\text{C}}$ under $1\;{\text{atm}}$, (b) $ - {6{0}^{0}}{\text{C}}$ under $10\;{\text{atm}}$, (c)${{15}^{0} }{\text{C}}$under 56 atm?

Ans: (a) The $P - T$ phase diagram for ${\text{C}}{{\text{O}}_2}$ is shown in the following figure.

${\text{C}}$ is the triple point of the ${\text{C}}{{\text{O}}_2}$ phase diagram. This indicates that with the current temperature and pressure corresponding to this point (i.e., at $ - {{56.6}^{0} }{\text{C}}$ and $5.11\;{\text{atm}}$ ), the solid, liquid, and vaporous phases of ${\text{C}}{{\text{O}}_2}$ co-exist in equilibrium.

2. The boiling and fusion points of

${\text{C}}{{\text{O}}_2}$ decrease with a decrease in pressure.

3. The temperature and pressure at which the critical temperature and pressure of ${\text{C}}{{\text{O}}_2}$ are 31.1 ${\text{C}}$ and 73 atm respectively. Even if it is squeezed to a higher pressure $^{73\;{\text{atm}},{\text{C}}{{\text{O}}_2}}$ will not liquefy if the temperature above the critical point.

4. The conclusion may be drawn from the $P - T$ phase diagram of ${\text{C}}{{\text{O}}_2}$ that:

1. ${\text{C}}{{\text{O}}_2}$ is gaseous at $ - {7{0}^{0} }{\text{C}}$, under 1 atm pressure

2. ${\text{C}}{{\text{O}}_2}$ is solid at $ - {6{0}^{0} }{\text{C}}$, under 10 atm pressure

3. ${\text{C}}{{\text{O}}_2}$ is liquid at ${{15}^{0} }{\text{C}}$, under 56 atm pressure

7.Answer the following questions based on the $P - T$ phase diagram of ${\text{C}}{{\text{O}}_2}$ :

(a) ${\text{C}}{{\text{O}}_2}$ at 1 atm pressure and temperature $ - {6{0}^{0} }{\text{C}}$ is compressed isothermally. Does it go through a liquid phase?

(b) What happens when ${\text{C}}{{\text{O}}_2}$ at 4 atm pressure is cooled from room temperature at constant pressure?

(c) Describe qualitatively the changes in a given mass of solid ${\text{C}}{{\text{O}}_2}$ at $10\;{\text{atm}}$ pressure and temperature $ - {{65}^{0} }{\text{C}}$ as it is heated up to room temperature at constant pressure.

(d) ${\text{C}}{{\text{O}}_2}$ is heated to a temperature ${7{0}^{0} }{\text{C}}$ and compressed isothermally. What changes

in its properties do you expect to observe?

Ans: (a) No

(b) It instantly condenses into a solid

(c) The intersection point where this parallel line cuts the fusion and vaporisation curves gives the fusion and boiling points.

(d) As pressure increases, it deviates from ideal gas behaviour.

Explanation:

(a) The $P - T$ phase diagram for ${\text{C}}{{\text{O}}_2}$ is shown in the following figure.

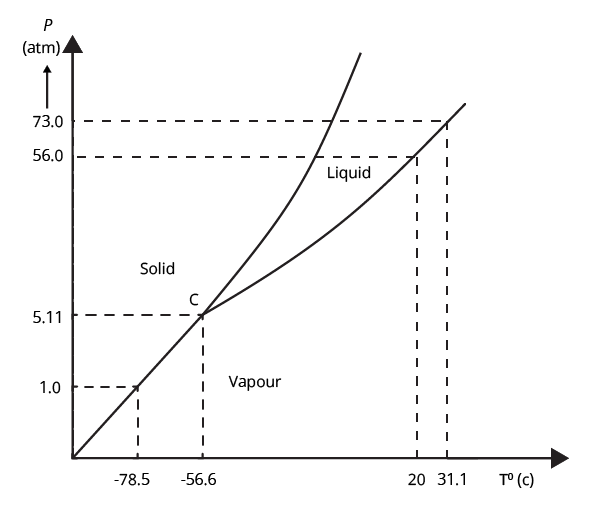
At 1 atm pressure and at $ - {6{0}^{0} }{\text{C}},{\text{C}}{{\text{O}}_2}$ lies to the left of $ - {{56.6}^{0} }{\text{C}}$ (triple point C) As a result, it exists in between the vaporous and solid phases.

Thus, ${\text{CC}}{{\text{O}}_2}$ Without passing through the liquid state, it immediately condenses into a solid.

(b) At 4 atm pressure, ${\text{C}}{{\text{O}}_2}$ lies below $5.11({\text{triple point}}\left. {\text{C}} \right)$. As a result, it exists between the vaporous and solid phases. As a result, it condenses directly into the solid form without going through the liquid stage.

(c) When the temperature of a mass of solid ${\text{C}}{{\text{O}}_2}$$({\text{at}}10\,{\text{atm}}\,{\text{pressure}}\,{\text{and}}\,{\text{at}}\, - {65^ \circ }{\text{C)}}$ is increased, It transitions from a solid to a liquid, and subsequently to a vaporous state. At 10 atm, it forms a line parallel to the temperature axis. The junction point where this parallel line cuts the fusion and vaporisation curves determines the fusion and boiling points

(d) If${\text{C}}{{\text{O}}_{\text{2}}}$ is heated to ${7{0}^{0} }{\text{C}}$ and If it is squeezed isothermally, there will be no transition to liquid state. This is because ${7{0}^{0} }{\text{C}}$ is higher than the critical temperature of ${\text{C}}{{\text{O}}_2}$. It will stay in the vapour state, but when pressure rises, it will deviate from its optimum behaviour.

8. A child running a temperature of ${101^ + }{\text{F}}$ is given an antipyrine (i.e. a medicine that lowers fever) which causes an increase in the rate of evaporation of sweat from his body. If the fever is brought down to ${{98}^{0} }{\text{F}}$ in $20\;{\text{min}}$, what is the average rate of extra evaporation caused, by the drug? Assume the evaporation mechanism to be the only way by which heat is lost. The mass of the child is $30\;{\text{kg}}$. The specific heat of human body is approximately the same as that of water, and latent heat of evaporation of water at that temperature is about $580{\text{cal}}{g^{ - 1}}$

Ans: The child's initial body temperature is ${T_1} = {{101}^{0} }{\text{F}}$

The child's final body temperature is ${T_2} = {{98}^{0} }{\text{F}}$

Change in temperature, $\Delta T = {\left[ {(101 - 98) \times \dfrac{5}{9}} \right]^ - }{\text{C}}$

Time taken to get the temperature down,

$t = 20\;{\text{min}}$

Mass of the child, $m = 30\;{\text{kg}} = 30 \times {10^3}\;{\text{g}}$

Specific heat of the human body = Specific heat of water $ = c$

$ = 1000{\text{cal}}/{\text{kg}}{/^6}{\text{C}}$

Calorific value of latent heat of water evaporation. $L = 580$ cal ${g^{ - 1}}$ The following is the amount of heat lost by the child:

$  {\Delta \theta  = mC\Delta T} $ 

$  { = 30 \times 1000 \times (101 - 98)\dfrac{5}{9}}$

$  { = 50000{\text{cal}}} $

Let, ${m_1}$ be the volume of water evaporated from the child's body in $20\;{\text{min}}$. The following factors contribute to heat loss through water:

$  {\Delta \theta  = {m_1}L} $

$  {\therefore {m_1} = \dfrac{{\Delta \theta }}{L}} $

$  { = \dfrac{{50000}}{{580}} = 86.2\;{\text{g}}} $

$\therefore $ The drug's average rate of additional evaporation

$ = \dfrac{{{m_1}}}{t}$

$ = \dfrac{{86.2}}{{200}} = 4.3\;{\text{g}}/{\text{min}}$

9.A brass boiler has a base area of $0.15\;{{\text{m}}^2}$ and thickness $1.0\;{\text{cm}}$. It boils water at the rate of $6.0\;{\text{kg}}/$ min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass $ = {10^9}J\;{{\text{s}}^{ - 1}}\;{{\text{m}}^{ - 1}}{K^{ - 1}}$ Heat of vaporisation of water $ = 2256 \times {10^3}J\;{\text{k}}{{\text{g}}^{ - 1}}$.

Ans: The boiler's base area, $A = 0.15\;{{\text{m}}^2}$

The boiler's thickness, $l = 1.0\;{\text{cm}} = 0.01\;{\text{m}}$

Water is boiling at a rapid rate, $R = 6.0\;{\text{kg}}/{\text{min}}$

Mass, $m = 6\;{\text{kg}}$

Time, $t = 1\min  = 60\;{\text{s}}$

Brass's thermal conductivity, $K = {1{0}^{0} }{\text{J}}{{\text{s}}^{ - 1}}\;{{\text{m}}^{ - 1}}{K^{ - 1}}$

Vaporization heat, $L = 2256 \times {10^3}J\;{\text{k}}{{\text{g}}^{ - 1}}$

The quantity of heat that passes through the boiler's brass base and into the water is calculated as follows:

$\theta  = \dfrac{{KA\left( {{T_1} - {T_2}} \right)t}}{l}$ …………(i)

Where,

${T_1} = $ The temperature of the flame that comes into contact with the boiler.

${T_2} = $ Boiling point of water $ = {10{0}^{0} }{\text{C}}$

Heat required for boiling the water: $\theta  = mL \ldots (ii)$

By combining equations (i) and (ii), we obtain:

$  {\therefore ml = \dfrac{{KA\left( {{T_1} - {T_2}} \right)t}}{l}} $

$  {{T_1} - {T_2} = \dfrac{{mLl}}{{KAt}}} $

$  { = \dfrac{{6 \times 2256 \times {{10}^3} \times 0.01}}{{109 \times 0.15 \times 60}}}$

$  { = {{137.98}^{0} }{\text{C}}} $

Therefore, the temperature of the portion of the flame that comes into contact with the boiler is ${{137.98}^{0} }{\text{C}}$.

10.Explain why:

(a) a body with large reflectivity is a poor emitter

(b) a brass tumbler feels much colder than a wooden tray on a chilly day

(c) an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace

(d) the earth without its atmosphere would be inhospitably cold

(e) heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water

Ans: (a) A body with a high reflectivity absorbs light radiations poorly. A poor radiation absorber will also be a poor radiation emitter. As a result, a body with a high reflectivity is an inefficient emitter.

(b) Brass is an excellent heat conductor. When a person touches a brass tumbler, heat is easily transferred from the body to the tumbler. As a result, the body's temperature drops to a lower level, and one feels cooler.

Wood is a poor heat conductor. When one touches a wooden tray, just a small amount of heat is transferred from the body to the tray. As a result, there is only a minor reduction in body temperature, and one does not feel cool. On a cool day, a metal tumbler seems colder than a wooden tray.

(c) The temperature of a red hot iron piece maintained in the open is measured incorrectly by an optical pyrometer calibrated for perfect black body radiation. The equation for black-body radiation is:

$E = \sigma \left( {{T^4} - T_0^4} \right)$

Where,

$E = $ Energy radiation

$T = $ Temperature of optical pyrometer

${T_0} = $ Temperature of open space

$\sigma  = $ Constant

As a result, increasing the temperature of open space lowers the amount of energy radiated. When the same piece of iron is heated in a furnace, the amount of radiation energy produced is the same $E = \sigma {T^4}$

(d) Earth would be inhospitably cold without its atmosphere. There will be no additional heat trapped in the absence of air gases. The heat would be reflected back to the surface of the earth.

(e) A heating system that circulates steam rather than hot water is more efficient in warming a building. This is due to the fact that steam includes latent heat, which is surplus heat.

$(540{\text{cal}}/{\text{g}})$

11. A body cools from ${8{0}^{0} }{\text{C}}$ to ${5{0}^{0} }{\text{C}}$ in 5 minutes. Calculate the time it takes to cool from ${6{0}^{0} }{\text{C}}$ to ${3{0}^{0} }{\text{C}}$. The temperature of the surroundings is ${2{0}^{0} }{\text{C}}$. 

Ans: We have the following, according to Newton's law of cooling:

$  { - \dfrac{{dT}}{{dt}} = K\left( {T - {T_0}} \right)}$

$  {\dfrac{{dT}}{{K\left( {T - {T_0}} \right)}} =  - Kdt} $

Where,

The body's temperature $ = T$

The temperature of the environment $ = {T_0} = {2{0}^{0} }{\text{C}}$

$K$ is a constant

The body's temperature drops from ${8{0}^{0} }{\text{C}}$ to ${5{0}^{0} }{\text{C}}$ In time, $t = 5\;{\text{min}} = 300\;{\text{s}}$ Integrating equation (j), we get:

$  {\int_{50}^{90} {\dfrac{{dT}}{{K\left( {T - {T_0}} \right)}}}  =  - \int_0^{300} K dt}$

$  {\left[ {{{\log }_e}\left( {T - {T_0}} \right)} \right]_{30}^{80} =  - K[t]_0^{3\infty }} $

$  {\dfrac{{2.3026}}{K}{{\log }_{10}}\dfrac{{80 - 20}}{{50 - 20}} =  - 300} $

$  {\dfrac{{2.3026}}{K}{{\log }_{10}}2 =  - 300} $

$  {\dfrac{{ - 2.3026}}{K}{{\log }_{10}}2 = K} $

The body's temperature drops from ${6{0}^{0} }{\text{C}}$ to ${3{0}^{0} }{\text{C}}$ in time $ = {t^\prime }$ Therefore, we get:

${\dfrac{{ - 2.3026}}{t}{{\log }_{10}}\dfrac{{60 - 20}}{{30 - 20}} =  - t} $

${\dfrac{{ - 2.3026}}{t}{{\log }_{10}}4 = K} $

We obtain the following when we combine equations (ii) and (iii):

${\dfrac{{ - 2.3026}}{t}{{\log }_{10}}4 = \dfrac{{ - 2.3026}}{{300}}{{\log }_{10}}2} $

${\therefore t = 300 \times 2 = 600s = 10\;{\text{min}}} $

Therefore, the time taken to cool the body from ${6{0}^{0} }{\text{C}}$ to ${3{0}^{0} }{\text{C}}$ is 10 minutes.