Important Questions for CBSE Class 11 Physics Chapter 12 - Kinetic Theory

1 Marks Questions

1. Given Samples of $1\;{\text{c}}{{\text{m}}^3}$ of Hydrogen and $1\;{\text{c}}{{\text{m}}^3}$ of oxygen, both at N. T. P. which sample has a larger number of molecules?

Ans: Equal volumes of all gases, at equivalent temperatures and pressures, contain the same number of molecules, according to Avogadro's hypothesis. As a result, the number of molecules in both samples is the same. As a result, the number of molecules in both samples is the same.

2. Find out the ratio between most probable velocity, average velocity and root Mean Square Velocity of gas molecules?

Ans : Since,

Most Probable velocity, ${V_{mP}} = \sqrt {\dfrac{{2KT}}{m}} $

Average velocity, $\bar V = \sqrt {\dfrac{{8KT}}{{\pi m}}} $

Root Mean Square velocity: Vr.m.s. $ = \sqrt {\dfrac{{3KT}}{m}} $

Now, find out the Ratio between most probable velocity, average velocity and root mean square velocity of gas molecules

So, ${{\text{V}}_{ = p}}:\overline {\text{V}} {\text{Vrm}}.{\text{s}} = \sqrt {\dfrac{{2{\text{KT}}}}{m}} :\sqrt {\dfrac{{3KT}}{{\pi m}}} :\sqrt {\dfrac{{3{\text{KT}}}}{m}} $

$ = \sqrt 2 :\sqrt {\dfrac{8}{\pi }} :\sqrt 3 $
${{\text{V}}_{ = \rho }}:\overline {\text{V}} $ Vr.m.s. $ = 1.1.3:1.23$

3. What is Mean free path?

Ans: The average distance a molecule travels between collisions is known as the mean free path. It is symbolised by (lambda). Meters are the units of measurement (m).

4. What happens when an electric fan is switched on in a closed room?

Ans: When an electric fan is turned on, electrical energy is first transferred into mechanical energy, which is subsequently converted into heat. Heat energy increases the kinetic energy of air molecules, raising the temperature of the environment.

5. State the law of equi- Partition  of energy?

Ans: The average kinetic energy of a molecule in each degree of freedom is equal to $\dfrac{1}{2}KT$.  According to the law of equipartition of energy. 

6. On what factors, does the average kinetic energy of gas molecules depend?

Ans: The absolute temperature is the only variable that affects average kinetic energy, and it is directly proportional to it.

7. Why the temperature less than absolute zero is not possible?

Ans: Since mean square velocity is proportional to temperature, it's a no-brainer. If the temperature is 0, the mean square velocity is also zero, and since molecules cannot be negative, temperatures lower than the absolute zone are not attainable.

8. What is the relation between pressure and kinetic energy of gas?

Ans: We are aware of this, Pressure$ = P$ Kinetic energy $ = {\text{E}}$

Now, Kinetic theory of gases is $P = \dfrac{1}{3}S{c^2} \to 1$ )

${\text{S}} = $ Density

$C = r.m.s$ Velocity of gas molecules

Translation’s mean kinetic energy per unit

Volume of the gas $ = E = \dfrac{1}{2}S{c^2} \to 2$ )

Dividing 1) by 2)

Now, we find out relation between pressure and kinetic energy of gas: 

$\dfrac{P}{E} = \dfrac{{1S{c^2}2}}{{3 \times S{c^2}}} = \dfrac{2}{3}$

$ \Rightarrow P = \dfrac{2}{3}E$

9. What is an ideal perfect gas?

Ans: Ideal gas is defined as a gas that obeys the following laws or qualities.

1) The size of a gas molecule is zero.

2) There is no attraction or repellent force between gas molecules.

2 Marks Questions

1. If a certain mass of gas is heated first in a small vessel of volume ${{\text{V}}_1}$ and then in a large vessel of volume ${{\text{V}}_2}$. Draw the ${\text{P}}$ - T graph for two cases?

Ans: Equation of perfect gas; $P = \dfrac{{RT}}{V}$

Given, temperature is  $P\alpha \dfrac{1}{V}$ As a result, when the gas is heated in a small vessel .

${V}_{1}$ the pressure rises faster than when the gas is heated in a big vessel  (Volume). 

${V}_{2}$  As a result, the slope of the graph in the case of a small vessel will be greater than in the case of a large vessel.

2. Derive the Boyle's law using kinetic theory of gases?

Ans: With the temperature constant, Boyle's law states that the volume of a given quantity of gas is inversely proportional to the pressure P, i.e. PV = constant.

The pressure exerted by a gas is now given by the kinetic theory of gases.

${\text{P}} = $ Pressure

${\text{V}} = $ Volume

$\overline {\text{V}}  = $ Average Velocity

${\text{m}}$ = Mass of 1 molecule

${\text{N}} = $ No. of molecules

${\text{M}} = {\text{mN}}$ (Mass of gas)

$P = \dfrac{{1mN{{\bar V}^2}}}{{3V}}$

${P_V} = \dfrac{1}{3}M{\bar V^2}$

3. At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the r.m.s speed of a helium gas atom at- ${{20}^{0} }{\text{C}}$ ? Given Atomic Mass is ${\text{Ar}} = 39.9$ and  ${\text{He}} = 4.0?$

Ans: Let we know that   , Vr.m.s.  and ${{\text{V}}^1}{\text{r}}$.m.s. are the root mean square speeds of Argon and helium

We have , Atoms  at temperature ${\text{T}}$ and ${{\text{T}}^1}$ respectively.

${\text{R}} = $ Universal Gas constant

${\text{T}} = $ Temperature

${\text{M}}$ = Atomic Mass of Gas

Now,   Vr.m.s. $ = \sqrt {\dfrac{{3RT}}{M}} $

${{\text{V}}^1}{\text{r}} \cdot {\text{m}}.{\text{s}}. = \sqrt {\dfrac{{3R{T^1}}}{{{M^1}}}} $

Given,${\text{M}} = $ Mass of Argon $ = 39.9$

${{\text{M}}^1} = $ Mass of Helium $ = 4.0$

${{\text{T}}^1} = $ Temperature of helium $ =  - {20^0}{\text{C}}$

${{\text{T}}^1} = 273 + ( - 20) = 253\;{\text{K}}$

${\text{T}} = $ Temperature of Argon =?

Now, Vr.m.s. = ${{\text{V}}^1}{\text{r}} \cdot {\text{m}}.$

$\sqrt {\dfrac{{3RT}}{M}}  = \sqrt {\dfrac{{3R{T^1}}}{{{M^1}}}} $

Squaring both side,

$\dfrac{{\not 3\,\not RT}}{M} = \dfrac{{\not 3\,\not R{T^1}}}{{{M^1}}}$

$\dfrac{T}{M} = \dfrac{{{T^1}}}{{{M^2}}} \Rightarrow T = \dfrac{{{T^1}M}}{{{M^1}}}$

Now it's time to put the numbers together.${T^1},{M^1}{\text{ \&  }}M$

$T = \dfrac{{253 \times 39.9}}{{4.0}} = 2523.7\;{\text{K}}$

4. Show that constant - temperature bulk modulus ${\text{K}}$ of an ideal gas is the pressure ${\text{P}}$ of the gas?

Ans: When a substance P is exposed to increased pressure, a minor fractional volume drop occurs, which is related to bulk modulus k by:-

$K = \dfrac{{\Delta P}}{{\dfrac{{ - \Delta V}}{V}}} \to 1$)

So we know that A negative sign implies that the volume is decreasing. Before,  compression in the case of an ideal gas at a constant temperature.

$PV = \dfrac{m}{M}RT \to 2$)

${\text{M}}$ = Molecular Mass of gas

We have, After compression at constant temperature,

$(P + \Delta P)(V + \Delta V) = \dfrac{m}{M}RT$

Now, From equation 2)

$PV = (P + \Delta P)(V + \Delta V)$

$P{V^\prime } = {P^\prime }{V^\prime } + P\Delta V + V\Delta P + \Delta P\Delta V$

or $ - P\Delta V = V\Delta P + \Delta P\Delta V$

$ - \dfrac{{P\Delta V}}{V} = \Delta P + \dfrac{{\Delta P\Delta V}}{V}(\because $ Dividing by ${\text{V}}$ on both sides )

$ - \dfrac{{P\Delta V}}{V} = \Delta P\left( {1 + \dfrac{{\Delta V}}{V}} \right)$

$ - \dfrac{{\Delta V}}{V} = \dfrac{{\Delta P}}{P}\left( {1 + \dfrac{{\Delta V}}{V}} \right)$

We're only concerned with minor fractional changes. Therefore, $\dfrac{{\Delta V}}{V}$ is much smaller than

1, As a result, it can be neglected as compared to 1.

$\therefore  - \dfrac{{\Delta V}}{V} = \dfrac{{\Delta P}}{P}$

Using this value instead of $\dfrac{{\Delta V}}{V}$ in equation 1) we get

$K = \dfrac{{\Delta P}}{{\dfrac{{\Delta P}}{P}}} = P$

As a result, the bulk modulus of an ideal gas is equal to the gas's pressure under compression at constant temperature.

5. The earth without its atmosphere would be inhospitably cold. Explain Why?

Ans: Infrared radiation from the earth's surface is reflected back to the lower layers of the atmosphere. As a result, the earth's heat radiation from the sun is trapped by the atmosphere during the day. The earth's surface would become too cold to live if it didn't have an atmosphere.

6. If a vessel contains 1 mole of ${0_2}$ gas (molar mass 32 ) at temperature ${\mathbf{T}}$. The pressure of the gas is P. What is the pressure if an identical vessel contains 1 mole of Hit at a temperature $2{\text{T}}?$

Ans: According to the ideal gas equation: $ \to $

$PV = nRT$

$P = $ pressure

${\text{V}}$ =volume

${\text{n}} = {\text{No}}$. of molecule per unit volume

R=Universal Gas Constant

${\text{T}} = $ Temperature

So we get, $\dfrac{{PV}}{T} = nR\quad $ or $\dfrac{{PV}}{T} = $ constant

Hence $\left. {\dfrac{{{P_1}{V_1}}}{{{T_1}}} = \dfrac{{{P_2}{V_2}}}{{{T_2}}} \to 1} \right)$

Now, in response to the query,$ \to $

${P_1} = P\mid {T_1} = T$

${V_1} = V\mid {T_2} = 2T$

Using above equations in equation 1)

${P_2} = \dfrac{{{P_1}{V_1}}}{{{T_1}}}K\dfrac{{{T_2}}}{{{V_2}}}$

${P_2} = \dfrac{{PV}}{T}X\dfrac{{2T}}{V}\quad \;{{\text{V}}_1} = {{\text{V}}_2} = {\text{V}}(\because $ identical vessels )

${{\text{P}}_2} = 2{\text{P}}$

As a result, the pressure is doubled.

7. At very low pressure and high temperature, the real gas behaves like ideal gas. Why?

Ans: An ideal gas has a molecule volume of zero and no intermolecular forces. 

1) At extremely low pressures, the amount of gas is so huge that the volume of a molecule is insignificant in comparison to the volume of gas.

2) Because the kinetic energy of molecules is very high at very high temperatures, the effect of intermolecular forces can be ignored.

As a result, at low pressure, real gases behave like an ideal gas.

8. Calculate the degree of freedom for monatomic, diatomic and triatomic gas?

Ans: The system's degrees of freedom are determined by:- ${\text{f}} = 3\;{\text{N}} - {\text{K}}$

Where, ${\text{f}} = $ degrees of freedom

${\text{N}} = $ Number of  Particles in the system.

${\text{K}} = $ Independent  relation among the particles.

Now ,

1) For a monatomic gas, ${\text{N}} = 1$ and ${\text{K}} = 0$

${\text{f}} = 3{\times }1 - 0 = 3$

2) For a diatomic gas; ${\text{N}} = 2$ and ${\text{K}} = {\text{m}}1$

${\text{f}} = 3{\times }2 - 1 = 5$

3) For a triatomic gas; ${\text{N}} = 3$ and ${\text{K}} = 3$

${\text{f}} = 3{\times }3 - 3$

${\text{f}} = 6$

As a result, the degrees of freedom for monatomic, diatomic, and Triatomic particles are 3, 5, and 6 respectively.

9. Determine the volume of 1 mole of any gas at s. T. P., assuming it behaves like an ideal gas?

Ans: Using the ideal gas equation-

${\text{P}} = $ Pressure

${\text{V}} = $ Volume

${\text{n}} = {\text{No}}$. of moles of gas

${\text{R}} = $ Universal Gas Constant

${\text{T}} = $ Temperature

We have,

${\text{PV}} = {\text{nRT}}$

${\text{V}} = \dfrac{{nRT}}{P}$

Given is  , ${\text{n}} = 1$ mole; ${\text{R}} = 8.31\;{\text{J}}/{\text{mol}}/{\text{K}};{\text{T}} = 273\;{\text{K}}$

${\text{P}} = 1.01 \times {10^5}\;{\text{N}}\mid {{\text{m}}^2}$

${\text{V}} = \dfrac{{1 \times (8.31) \times 273}}{{1.01 \times {{10}^3}}}$

${\text{V}} = 22.4 \times {10^{ - 3}}\;{{\text{m}}^3}$

Since 1 litre

$ = 1000\;{\text{c}}{{\text{m}}^3}$

$ = 1 \times {10^{ - 3}}\;{{\text{m}}^3}$

Hence ${\text{V}} = 22.41$

i.e. at S.T.P., any gas has a volume of 22.41. (Standard Temperature & Pressure).

10. A tank of volume $0.3{m^3}$contains 2 moles of Helium gas at ${{20}^{0} }{\text{C}}$. Assuming the helium behave as an ideal gas;

Ans: 1) Find the total internal energy of the system.

Given, ${\text{n}} = $ No. of moles $ = 2$

${\text{T}} = $ Temperature $ = 273 + 20 = 293\;{\text{K}}$

${\text{R}} = $ Universal Gas constant $ = 8.31\;{\text{J}}/{\text{mole}}.$

So we know that, Total energy of the system $ = {\text{E}} = \dfrac{3}{2}nRT$

Hence, $E = \dfrac{3}{2} \times n \times 8.31 \times 293E = 7.30 \times {10^3}J$

 2) Determine the r. m. s. Speed of the atoms.

 Molecular Mass of helium $ = 4\;{\text{g}}$ \ mol

$ = \dfrac{{4 \times {{10}^{ - 3}}{\text{Kg}}}}{{mol}}$

Now , Root Mean speed $ = {\text{Vr}} \cdot {\text{m}} \cdot {\text{s}} = \sqrt {\dfrac{{3RT}}{M}}  = \sqrt {\dfrac{{3X8.31 \times 293}}{{4X{{10}^{ - 3}}}}} $

Vr.m.s. $ = 1.35{\text{X}}{10^3}\;{\text{m}}/{\text{s}}$

11. State Graham's law of diffusion and derive it?

Ans: The rates of diffusion of two gases are inversely proportional to the square roots of their densities, according to Graham's law of diffusion.

Consider two gases diffusing into one another at a certain pressure. Let ${{\text{S}}_{\text{A}}}$ and ${{\text{S}}_{\text{B}}}$ be their densities. 

So we know that, the root Mean square velocities of the molecules of gases A and B will be: $ \to $

$\left. {{{\text{V}}^{\text{A}}}{\text{r}} \cdot {\text{m}} \cdot {\text{s}} = \sqrt {\dfrac{{3P}}{{{S_A}}}}  \to 1} \right)$

$\left. {{{\text{V}}^{\text{B}}}{\text{r}} \cdot {\text{m}} \cdot {\text{s}} = \sqrt {\dfrac{{3P}}{{{S_\mathbb{B}}}}}  \to 2} \right)$

Now, Dividing equation 1) by 2)

$\left. {\dfrac{{{{\text{V}}^A}{\text{r}} \cdot {\text{m}} \cdot {\text{s}}.}}{{{{\text{V}}^{\text{B}}}{\text{r}} \cdot {\text{m}}.{\text{s}}}} = \sqrt {\dfrac{{3P}}{{{S_A}}}} X\sqrt {\dfrac{{{S_B}}}{{3P}}} \quad  = \sqrt {\dfrac{{{S_B}}}{{{S_A}}}}  \to 1} \right)$

The rate of diffusion of a gas is now directly related to its molecules' r.m.s. velocity. If and are the gas diffusion rates, and B is the rate of diffusion of gases, then

$\dfrac{{{r_A}}}{{{r_B}}} = \dfrac{{{V^A}rm.s}}{{{V^B}{r_M}.s}} = \sqrt {\dfrac{{{S_B}}}{{{S_A}}}} $

Or $ \Rightarrow $ this is Graham's law.

$\dfrac{{{r_A}}}{{{r_B}}} = \sqrt {\dfrac{{{S_B}}}{{{S_A}}}} $

12. State Charles's law? If air is filled in a vessel At ${{60}^{0}}{\text{c}}$. To what temperature should it be heated in order that $\dfrac{{{1^{rd}}}}{3}$ of air may escape out of the vessel?

Ans: According to Charles' law, the volume of a given mass of a gas is precisely proportional to its Kelvin temperature when pressure remains constant, i.e.

V & T if pressure is constant; ${\text{V}} = $ volume ${\text{T}} = $ Temperature

Or $\dfrac{V}{T} = $ constant

We have, ${{\text{T}}_1} = 60 + 273 = 333{\text{k}}$

${{\text{v}}_1} = {\text{V}}$

${{\text{T}}_2} = $ ?

${{\text{v}}_2} = {\text{V}} + \dfrac{V}{3} = \dfrac{4}{3}V$

So now , from Charles's show,

$\dfrac{{{V_1}}}{{{T_1}}} = \dfrac{{{V_2}}}{{{T_2}}} \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{T_1}}}{{{T_2}}}$

${{\text{T}}_2} = {{\text{T}}_1}\dfrac{{{V_2}}}{{{V_1}}}$

${{\text{T}}_2}\dfrac{{333 \times 4\;{\text{V}}}}{{3 \times V}}$

Hence,

${{\text{T}}_2} = {171^0}{\text{c}}$ or $444{\text{k}}$

13. Show that average kinetic energy of translation per molecule of gas is directly proportional to the absolute temperature of gas?

Ans: According to the kinetic theory of gases, one mole of an ideal gas exerts a pressure of

${\text{P}} = \dfrac{{1M{C^2}}}{{3\;{\text{V}}}}\quad {\text{M}} = $ Mass of gas

or ${\text{PV}} = \dfrac{{1M{C^2}}}{3}\;{\text{V}} = $ Volume of gas

Since ${\text{PV}} = {\text{RT}}$ (for 1mole of gas)

or $\dfrac{1}{3}M{C^2} = RT\quad $ R=Universal gas constant

${C^2} = \dfrac{{3RT}}{M}\quad \;{\text{T}} = $ Temperature

So Now, $C\alpha \sqrt T $

Also, $\dfrac{1}{3}M{C^2} = RT$

Dividing by number of molecules of gas $ = {\text{N}}$

$\dfrac{{1M}}{{3N}}{C^2} = \dfrac{R}{N}T$

${\text{K}} = $ Boltzman constant

$\dfrac{1}{3}m{c^2} = KT \to $ Dividing

or $\dfrac{1}{2}m{c^2} = \dfrac{3}{2}KT$

We get , $\dfrac{1}{2}m{c^2} = $ Kinetic energy per molecule of gas

Now, $\dfrac{1}{2}m{c^2}\alpha T$

as $\dfrac{3}{2}k = $ constant

14. Air pressure in a car tyre increases during driving? Why?

Ans: Because of the action, the temperature of the air inside the tyre rises during driving. According to Charles's law, as the temperature rises, the pressure inside the tyres rises as well.

15. Four molecules of gas have Speeds $2,4,6,8,\;{\text{km}}/{\text{s}}$. Respectively.

Ans: Here, ${{\text{C}}_1} = {\text{km}}/{\text{s}} = $ velocity of first gas

${{\text{C}}_2} = 4\;{\text{km}}/{\text{s}}$ l=velocity of second gas

${{\text{C}}_3} = 6\;{\text{km}}/{\text{s}} = $ velocity of third gas

${{\text{C}}_4} = 8\;{\text{km}}/{\text{s}}$ =velocity of fourth gas

1) Average speed -

Calculate the average period –

We Get used formula is,

$\therefore $ Average speed $ = \dfrac{{{C_1} + {C_2} + {C_3} + {C_4}}}{4}$

Now,

Average Speed $ = \dfrac{{2 + 4 + 6 + 8}}{4}$

i.e Average Speed $ = \dfrac{{20}}{4} = 5\;{\text{km}}/{\text{s}}$

2) Root Mean square speed -

Calculate the Root mean square speed –

We Get used formula is, 

Root Mean Square Speed $ = \sqrt {\dfrac{{C_1^2 + C_2^2 + C_3^2 + C_4^2}}{4}} $

Now ,

R. m. s of gas$ = \sqrt {\dfrac{{{2^2} + {4^2} + {6^2} + {8^2}}}{4}} $

R. m. s of gas$ = \sqrt {\dfrac{{120}}{4}} $

i.e R. m. s of gas$ = 5.48km/s$

3 Marks Questions

1.  If Nine particles have speeds of $5,8,12,12,12,14,14,17$and $20\;{\text{m}}/{\text{s}}$. Find.

Ans:  1) the average speed

Divide the total number of particles by the sum of their speeds to get the average speed.

Hence, Average speed, $\bar V = \dfrac{{5 + 8 + 12 + 12 + 12 + 14 + 14 + 17 + 20}}{9} = 12.7\;{\text{m}}\mid {\text{s}}$

 2) the Most Probable speed

 The average value of the square of speeds is given by:-

Hence,${\bar V^2} = \dfrac{{{5^2} + {8^2} + {{12}^2} + {{12}^2} + {{12}^2} + {{14}^2} + {{14}^2} + {{17}^2} + {{20}^2}}}{9}$

$ = \dfrac{{25 + 64 + 144 + 144 + 144 + 196 + 196 + 289 + 400}}{9} = \dfrac{{1602}}{9}$

i.e. ${\bar V^2} = 178\;{{\text{m}}^2}/{{\text{s}}^2}$

RM $S$ speed,$Vrm.s = \sqrt {{{\bar V}^2}}  = \sqrt {178}  = 13.3\;{\text{m}}/{\text{s}}$

 3) the r.m.s. Speed of the particles

 Three particles have a speed of, two particles have a speed of, and the remaining particles have varying speeds. As a result, the most likely speed,

${{\text{V}}_{{\text{mP}}}} = 12\;{\text{m}}/{\text{s}}$

2: Establish the relation between $Y\left( { = \dfrac{{{C_P}}}{{{C_V}}}} \right)$ and degrees of freedom (n)?

Ans: Now $y = \dfrac{{{C_p}}}{{{C_V}}}$

Where ${\text{CP}} = $ specific heat at constant pressure

${\text{CV}} = $ Specific heat at Constant  volume.

and ${\text{n}} = $ Degrees of freedom $ \to $ is the total number of co-ordinates or independent quantities needed to completely describe the system's position and configuration.

 Suppose, a polyatomic gas molecule has ' ${{\text{n}}^\prime }$ degrees of freedom.

$\therefore $ Total energy associated with a gram molecule of the gas i. e.

Here,

${\text{N}} = $ Total number of molecules 

${\text{R}} = $ Universal Gas Constant

${\text{R}} = {\text{NK}}$

${\text{K}} = $ Boltzmann Constant

${\text{E}} = n \times \dfrac{1}{2}{\text{KT}} \times {\text{N}} = \dfrac{n}{2}RT$

So We know that,

Specific heat at constant volume,

${C_v} = \dfrac{{dE}}{{dT}}$

${C_V} = \dfrac{d}{{dT}}\left( {\dfrac{n}{2}RT} \right)$

${C_V} = \dfrac{n}{2}R$

Now Specific heat at constant Pressure, ${{\text{C}}_{\text{P}}} = {\text{Cv}} + {\text{R}}$

${C_P} = \dfrac{n}{2}R + R$

${C_P} = \left( {\dfrac{n}{2} + 1} \right)R$

As, $Y = \dfrac{{{C_p}}}{{{C_\nabla }}}$

$Y = \dfrac{{\left( {\dfrac{n}{2} + 1} \right)R}}{{\dfrac{n}{2}R}}$

$Y = \left( {\dfrac{n}{2} + 1} \right) \times \dfrac{2}{n}$

$Y = \dfrac{2}{{\not \prime }} \times \dfrac{{\not t}}{{{\gamma ^\prime }}} + 1 \times \dfrac{2}{n}$

Hence, $Y = \left( {1 + \dfrac{2}{n}} \right)$

3: Two perfect gases at absolute temperature ${{\text{T}}_1}$ and ${{\text{T}}_2}$ are mixed. There is no loss of energy. Find the temperature of the mixture if the masses of molecules are ${{\text{m}}_1}$ and ${{\text{m}}_2}$and number of molecules is ${{\text{n}}_1}$ and ${{\text{n}}_2}?$

Ans: There is no reciprocal interaction between the molecules in a perfect gas. Now, K.E of gas $ = \dfrac{1}{2}m{v^2}$

Energy equivalence is achieved by energy equivalence :

$\dfrac{1}{2}m{v^2} = \dfrac{3}{2}KT$

K.E of one gas $ = {n_1} \times \left( {\dfrac{3}{2}K{T_1}} \right) \to 1$ )

K.E. of other gas $ = {n_2} \times \left( {\dfrac{3}{2}K{T_2}} \right) \to 2$ )

Now , ${{\text{n}}_1},{{\text{n}}_2} = $ Number of molecules in gases

${\text{K}} = $ Bolt zman' Constant

${{\text{T}}_1},\;{{\text{T}}_2} \to $ Temperatures.

Total K.E. $ = \dfrac{3}{2}K\left( {{n_1}{T_1} + {n_2}{T_2}} \right)$ (adding equation 1)\&2)

Let we know that, ${\text{T}}$ be the absolute temperature of the mixture of gases

Then,

Total Kinetic energy $ = {n_1} \times \left( {\dfrac{3}{2}KT} \right) + {n_2} \times \left( {\dfrac{3}{2}KT} \right)$

Total K.E $ = \dfrac{3}{2}KT\left( {{n_1} + {n_2}} \right) \to 4$ )

Since there is no loss of energy, hence on equating e$^43$ ) & 4) for total K.E.: $ \to $

$\dfrac{{\not 3}}{{\not 2}}\not KT({n_1} + {n_2}) = \dfrac{{\not 3}}{{\not 2}}\not K\left( {{n_1}{T_1} + {n_2}{T_2}} \right)$

$T\left( {{n_1} + {n_2}} \right) = \left( {{n_1}{T_1} + {n_2}{T_2}} \right)$

Therefore,$T = \dfrac{{{n_1}{T_1} + {n_2}{T_2}}}{{{n_1} + {n_2}}}$

4. Derive Avogadro's law?

Ans: Avogadro's law asserts that equal volumes of all gases, at the same temperature and pressure, have the same number of molecules. Consider two gases with similar volumes at the same temperature T  and pressure${{\text{P}}^\prime }$.

Let ${{\text{M}}_1}$ =Mass of first gas

${{\text{M}}_2} = $ Mass of second gas

${{\text{C}}_1} = {{\text{C}}_2} = {\text{r}}.{\text{m}}.{\text{s}}$ velocity of gas molecules of 2 gases ${\text{m}}1/{\text{m}}2 = $ Mass of each molecule of gas

${{\text{M}}_1},\;{{\text{m}}_2} = $ Number of molecules of gas

Now, ${{\text{M}}_1} = {{\text{m}}_1}{{\text{n}}_1}$ and ${{\text{M}}_2} = {{\text{m}}_2}{{\text{n}}_2}$

From kinetic theory of gas: -

For first gas $ \Rightarrow P = \dfrac{{1{M_1}}}{{3V}}C_1^2 \to (1)$

For second gas $ \Rightarrow P = \dfrac{{1{M_2}}}{{3V}}C_2^2 \to (2)$

Now, Equating equation 1) 82) for pressure

$\dfrac{{1{M_1}}}{{3V}}C_1^2 = \dfrac{{1{M_2}}}{{3V}}C_2^2$

$\left. {{{\text{M}}_1}{\text{c}}_1^2 = {\text{M}}_2^2{\text{C}}_2^2 \to 3} \right)$

$\dfrac{{{\text{ AverageK}}{\text{.E }}}}{{{\text{ Molecule of first gas }}}} = \dfrac{{{\text{ Average KE}}}}{{{\text{ Moleculeof sec ond gas }}}} \Rightarrow $ for same temperatures

$\dfrac{1}{2}{M_1}C_1^2 = \dfrac{1}{2}{M_2}C_2^2$

$\left. {{{\text{M}}_1}{\text{C}}_1^2 = {{\text{M}}_2}{{\text{C}}_2}^2 \to 4} \right)$

Let ${\text{Cl}},{\text{C}}2 - {\text{Cn}} = $ Random velocities of gases molecules

Let  Radom rectangular co-ordinates of $\eta $ - molecules

$x_1^2 + y_1^2 + z_1^2 = c_1^2$

So, ${x_n}^2 + {y_n}^2 + {z_n}^2 = {c_n}^2$

we have,

Initial Molomentum of ${\text{A}}, = {\text{m}}{{\text{x}}_1}$

on collision with wall, Momentum = -mx,

Change in Momentum $ =  - {\text{m}}{{\text{x}}_1} - {\text{m}}{{\text{x}}_1}$

$ =  - 2\;{\text{m}}{x_1}$

Let , The molecule in between the collisions of two walls OPKT and QRSL covers a distance $ = 2{\text{a}}$

So, time between 2 collisions $ = \dfrac{{2a}}{{{x_1}}}$

As Mornentum transferred in 1 second $ = 2\;{\text{m}}{x_1}{\text{x}}\dfrac{{{x_1}}}{{2a}} = \dfrac{{mx_{\text{g}}^2}}{a}$

From Newton's second law $ \Rightarrow {f_1} = \dfrac{{mx_1^2}}{a}$

$fn = \dfrac{{mx_n^2}}{a}$

Total force in ${\text{X}}$ -direction $ = {{\text{f}}_1} + {{\text{f}}_2} +  \ldots {\text{fn}}$

$ = \dfrac{{mx_1^2}}{a} + \dfrac{{mx_2^2}}{a} +  -  -  -  - \dfrac{{mx_h^2}}{a}$

Pressure exerted on wall QRSL

$ = \dfrac{{Fx}}{{{a^2}}} = \dfrac{m}{{{a^2}}}\left( {x_1^2 + x_2^2 +  -  -  -  - x_n^2} \right)$

Dividing equation 4 ) by 3 )

$\dfrac{{{M_1}C_1^2}}{{{m_1}c_1^2}} = \dfrac{{{M_2}C_2^2}}{{{m_2}c_2^2}}\quad M = m \times n$

$\dfrac{{{m_1}{n_1}}}{{{m_1}}} = \dfrac{{{m_2}{n_2}}}{{{m_2}}}$

$ \Rightarrow $ I.e. Avogadro's law

${{\text{n}}_1} = {{\text{n}}_2}$

5. What are the assumptions of kinetic theory of gas?

Ans: The following are the assumptions of the kinetic theory of gases:

1) A gas is made up of a vast number of molecules that should all be elastic spheres and identical.

2) A gas's molecules are in a constant state of rapid and unpredictable mobility.

3) Gas molecules are extremely small in comparison to the distance between them.

4) There is no attraction or repulsio between the molecules.

5) Molecule collisions with one another and with the vessel's walls are perfectly elastic.

6. Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be $3{{A}^{0} }$.

Ans: Given, Diameter of an oxygen molecule, $d = 3A$

Radius, $r = \dfrac{d}{2} = \dfrac{3}{2} = 1.5{\quad _A} = 1.5 \times {10^{ - 8}}\;{\text{cm}}$

We know that the Actual volume occupied by 1 mole of oxygen gas at $ TP = 22400\;{\text{c}}{{\text{m}}^3}$

Let Molecular volume of oxygen gas, $V = \dfrac{4}{3}\pi {r^3} - N$

Where, $N$ is Avogadro's number $ = 6.023 \times 1023$ molecules/mole

$\therefore V = \dfrac{4}{3}3.14 \times {\left( {1.5 \times {{10}^{ - 8}}} \right)^3} \times 6.023 \times {10^{23}} = 8.51\;{\text{c}}{{\text{m}}^3}$

Hence, the Ratio of the molecular volume to the actual volume of oxygen $ = \dfrac{{8.51}}{{22400}}$

$ = 3.8 \times {10^{ - 4}}$

7. Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity $25.0\;{{\text{m}}^3}$ at a temperature of ${{27}^{0} }{\text{C}}$.

Ans: Given is, Volume of the room, $V = 25.0\;{{\text{m}}^3}$

Temperature of the room, $T = {{27}^{0}}{\text{C}} = 300\;{\text{K}}$

Pressure in the room, $P = 1\;{\text{atm}} = 1 \times 1.013 \times {10^5}\;{\text{Pa}}$

We get, The ideal gas equation relating pressure $(P)$, Volume (V), and absolute temperature ( $T$ ) can be written as:

$PV = {k_B}NT$

Where,

${K_B}$ is Boltzmann constant $ = 1.38 \times {10^{ - 23}}\;{{\text{m}}^2}\;{\text{kg}}\;{{\text{s}}^{ - 2}}\;{{\text{K}}^{ - 1}}$

$N$ is the number of air molecules in the room

Now,

$\therefore N = \dfrac{{PV}}{{{k_5}T}}$

$ = \dfrac{{1.013 \times {{10}^5} \times 25}}{{1.38 \times {{10}^{ - 25}} \times 300}}$

$ = 6.11 \times {10^{26}}$ molecules

As a result, the total number of air molecules in a room is  $6.11 \times {10^{26}}$.

8. From a certain apparatus, the diffusion rate of hydrogen has an average value of $28.7$ ${\text{cm}}3\;{{\text{s}}^{ - 1}}$. The diffusion of another gas under the same conditions is measured to have an average rate of $7.2\;{\text{c}}{{\text{m}}^3}\;{{\text{s}}^{ - 1}}$. Identify the gas.(Hint: Use Graham's law of diffusion: ${{\text{R}}_1}/{{\text{R}}_2} = {\left( {{{\mathbf{M}}_2}/{{\mathbf{M}}_1}} \right)^{1/2}}$, where ${{\mathbf{R}}_1},{{\mathbf{R}}_2}$ are)

diffusion rates of gases 1 and 2 , and ${{\mathbf{M}}_1}$ and ${{\mathbf{M}}_2}$ their respective molecular masses. The law is a simple consequence of kinetic theory.)

Ans:  Given, 

Rate of diffusion of hydrogen, ${R_1} = 28.7\;{\text{c}}{{\text{m}}^3}\;{{\text{s}}^{ - 1}}$

Rate of diffusion of another gas, ${R_2} = 7.2\;{\text{c}}{{\text{m}}^3}\;{{\text{s}}^{ - 1}}$

According to Graham's Law of diffusion, we have:

$\dfrac{{{R_1}}}{{{R_2}}} = \sqrt {\dfrac{{{{\mathbf{M}}_2}}}{{{{\mathbf{M}}_1}}}} $

Where,

${M_1}$ is the molecular mass of hydrogen $ = 2.020\;{\text{g}}$

${M_2}$ is the molecular mass of the unknown gas

Now putting value in given,

$\therefore {{\mathbf{M}}_2} = {{\mathbf{M}}_1}{\left( {\dfrac{{{R_1}}}{{{R_2}}}} \right)^2}$

$ = 2.02{\left( {\dfrac{{28.7}}{{7.2}}} \right)^2} = 32.09\;{\text{g}}$

32 g is the oxygen molecular mass. As a result, oxygen is the unknown gas.

4 Marks Questions

1. Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure $0{}^\circ \text{C}$. Show that it is $22.4$ liters.

Ans: The relationship between pressure (P), volume (V), and absolute temperature (T) is known as the ideal gas equation.

$PV = $ net

Where,

$R$ is the universal gas constant $ = 8.314\;{\text{J}}\;{\text{mo}}{{\text{l}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

$n = $ Number of moles $ = 1$

$T = $ Standard temperature $ = 273\;{\text{K}}$

$P = $ Standard pressure $ = 1\;{\text{atm}} = 1.013 \times {10^5}{\text{N}}{{\text{m}}^{ - 2}}$

Formula is, 

$\therefore V = \dfrac{{nRT}}{P}$

Now put the value,

$ = \dfrac{{1 \times 8.314 \times 273}}{{1.013 \times {{10}^5}}}$

$ = 0.0224\;{{\text{m}}^3}$

i.e V$ = 22.4$ liters

As a result, a gas's molar volume at STP is 22.4 litres.

2. Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is the largest?

Ans: Yes. All of them have the same number of molecules in them.

No. Neon has the highest root mean square speed.

The three jars have the same volume because their capacities are equal.

As a result, the pressure, volume, and temperature of each gas are the same.

The three vessels will each contain an equal quantity of the corresponding molecules, according to Avogadro's law. This is the same as Avogadro's number.

$N = 6.023 \times {10^{23}}$.

The root mean square speed $\left( {{v_{{\text{ru}}}}} \right)$ of a gas of mass ${\text{m}}$, and temperature $T$, is given relation is :

${v_{r = }} = \sqrt {\dfrac{{3kT}}{m}} $

Here, $k$ is Boltzmann constant

As we know the given gases, $k$ and $T$ are constants.

Hence ${v_{{r_{14}}}}$ depends only on the mass of the atoms, i.e.,

${v_{rne}} \propto \sqrt {\dfrac{1}{m}} $

As a result, the root mean square speed of the molecules in each of the three scenarios differs. The mass of neon is the smallest of the three elements: neon, chlorine, and uranium hexafluoride. As a result, among the supplied gases, neon has the fastest root mean square speed

3. A metre-long narrow bore held horizontally (and closed at one end) contains a $76\;{\text{cm}}$long mercury thread, which traps a $15\;{\text{cm}}$ column of air. What happens if the tube is held vertically with the open end at the bottom?

Ans: Given By the  Length of the narrow bore, $L = 1\;{\text{m}} = 100\;{\text{cm}}$

Length of the mercury thread, $l = 76\;{\text{cm}}$

Length of the air column between mercury and the closed end, ${l_a} = 15\;{\text{cm}}$

Now,The mercury length that occupies the air space is because the bore is kept vertically in air with the open end at the bottom : $100 - (76 + 15) = 9\;{\text{cm}}$

Hence, the total length of the air column $ = 15 + 9 = 24\;{\text{cm}}$

Let $h\;{\text{cm}}$ of mercury flow out as a result of atmospheric pressure.

- Length of the air column in the bore $ = 24 + h\;{\text{cm}}$

And, length of the mercury column $ = 76 - h\;{\text{cm}}$

Initial pressure, ${P_1} = 76\;{\text{cm}}$ of mercury

Initial volume, ${V_1} = 15\;{\text{c}}{{\text{m}}^3}$

Final pressure, ${P_2} = 76 - (76 - h) = h\;{\text{cm}}$ of mercury

Final volume, ${V_2} = (24 + h){\text{c}}{{\text{m}}^3}$

Temperature remains constant throughout the process.

$\therefore {P_1}{V_1} = {P_2}{V_2}$

$76 \times 15 = h(24 + h)$

${h_2} + 24h - 1140 = 0$

$\therefore h = \dfrac{{ - 24 \pm \sqrt {{{(24)}^2} + 4 \times 1 \times 1140} }}{{2 \times 1}}$

$ = 23.8\;{\text{cm}}$ or $ - 47.8\;{\text{cm}}$

Height can't possibly be a disadvantage. As a result, 23.8 cm of mercury will flow out of the hole, leaving 52.2 in the chamber. The length of the air column will be. $24 + 23.8 = 47.8\;{\text{cm}}$.

4. An air bubble of volume $1.0\;{\text{cm}}3$ rises from the bottom of a lake $40\;{\text{m}}$ deep at a temperature of ${{35}^{0}}{\text{C}}$ ?

Ans: Given is, Volume of the air bubble, ${V_1} = 1.0\;{\text{c}}{{\text{m}}^3} = 1.0 \times {10^{ - 6}}\;{{\text{m}}^3}$

Bubble rises to height, $d = 40\;{\text{m}}$

Temperature at a depth of $40\ \text{m},{{T}_{1}}=12{}^\circ \text{C}=285\ \text{K}$

Temperature at the surface of the lake, ${{T}_{2}}=35{}^\circ \text{C}=308\ \text{K}$

The pressure on the surface of the lake:

${P_2} = 1\;{\text{atm}} = 1 \times 1.013 \times {10^5}\;{\text{Pa}}$

The pressure at the depth of $40\;{\text{m}}$ :

${P_1} = 1\;{\text{atm}} + d\rho {\text{g}}$

Given ,

$\rho $ is the density of water $ = {10^3}\;{\text{kg}}/{{\text{m}}^3}$

${\text{g}}$ is the acceleration due to gravity $ = 9.8\;{\text{m}}/{{\text{s}}^2}$

$\therefore {P_1} = 1.013 \times {10^5} + 40 \times {10^3} \times 9.8$

$ = 493300\;{\text{Pa}}$

We have: $\dfrac{{{P_1}{V_1}}}{{{T_1}}} = \dfrac{{{P_2}{V_2}}}{{{T_2}}}$

Where, ${V_2}$ is the volume of the air bubble when it reaches the surface

${V_2} = \dfrac{{P{V_1}{T_2}}}{{{T_1}{P_2}}}$

Now put the value,

$ = \dfrac{{(493300)\left( {1.0 \times {{10}^{ - 5}}} \right)308}}{{285 \times 1.013 \times {{10}^5}}}$

$ = 5.263 \times {10^{ - 6}}\;{{\text{m}}^3}$ or $5.263\;{\text{c}}{{\text{m}}^3}$

As a result, the volume of the air bubble decreases as it approaches the surface. $5.263\;{\text{c}}{{\text{m}}^3}$.

5. Estimate the average thermal energy of a helium atom at

Ans:  

(i) room temperature $\left( 27{}^\circ \text{C} \right)$

 At room temperature, calculate the average thermal energy of a helium atom. $T=27{}^\circ \text{C}=300\ \text{K}$

Now, Average thermal energy $= \dfrac{3}{2}kT$

Let,  $k$ is Boltzmann constant $= 1.38 \times {10^{ - 23}}\;{{\text{m}}^2}\;{\text{kg}}\;{{\text{s}}^{ - 2}}\;{{\text{K}}^{ - 1}}$

$\therefore \dfrac{3}{2}kT = \dfrac{3}{2} \times 1.38 \times {10^{ - 98}} \times 300$

$ = 6.21 \times {10^{ - 21}}J$

As a result, at ambient temperature, the average thermal energy of a helium atom is $\left({{27}^{0} }{\text{C}} \right)$ is $6.21 \times {10^{ - 21}}J$

(ii) the temperature on the surface of the Sun (6000 K) 

Determine the average thermal energy of a helium atom at the sun's surface.  $T = 6000\;{\text{K}}$

Now, Average thermal energy $ = \dfrac{3}{2}kT$

$\dfrac{3}{2} \times 1.38 \times {10^{ - 38}} \times 6000$

$ = 1.241 \times {10^{ - 18}}J$

As a result, a helium atom on the sun's surface has an average thermal energy of $1.241 \times {10^{ - 19}}J$

(iii) the temperature of 10 million Kelvin (the typical core temperature in the case of a star).

Find the average thermal energy of a helium atom  At temperature,  $T = 107\;{\text{K}}$

Now, Average thermal energy $ = \dfrac{3}{2}kT$

$\dfrac{3}{2} \times 1.38 \times {10^{ - 38}} \times {10^7}$

$ = 2.07 \times {10^{ - 16}}J$

As a result, the average thermal energy of a helium atom at a star's core is $2.07 \times {10^{ - 16}}J$.

6. At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at $ - {{20}^{0}}{\text{C}}?$ (atomic mass of ${\text{Ar}} = $ $39.9{\text{u}}$, of ${\text{He}} = 4.0{\text{u}}$ ).

Ans: Given data is,

Temperature of the helium atom, ${T_F} =  - {{20}^{0}}{\text{C}} = 253\;{\text{K}}$

Atomic mass of argon, ${M_A} = 39.9{\text{u}}$

Atomic mass of helium, ${M_{He}} = 4.0{\text{u}}$

Let, ${\left( {{v_{r = \infty }}} \right)_d}$ be the rms speed of argon.

Let ${\left( {{v_{rwe}}} \right)_{Ht}}$ be the rms speed of helium.

We have , The rms speed of argon is given by:

${\left( {{v_{n + \xi }}} \right)_A} = \sqrt {\dfrac{{3R{T_A}}}{{{M_{\Delta t}}}}} $

Where,

$R$ is the universal gas constant

${T_A}$ is temperature of argon gas

Now, The rms speed of helium is given by:

${\left( {{v_{rms}}} \right)_{Ht}} = \sqrt {\dfrac{{3R{T_R}}}{{{M_H}}}}  \ldots $ (ii)

It is given that:

${\left( {{v_{rre}}} \right)_{At}} = {\left( {{v_{rwb}}} \right)_B}$

$\sqrt {\dfrac{{3R{T_{AV}}}}{{{M_A}}}}  = \sqrt {\dfrac{{3R{T_B}}}{{{M_H}}}} $

$\dfrac{{{T_\Delta }}}{{{M_\Delta }}} = \dfrac{{{T_B}}}{{{M_{Ht}}}}$

${T_A} = \dfrac{{{T_{{H_t}}}}}{{{M_{{H_t}}}}} \times {M_\Delta }$

$ = \dfrac{{253}}{4} \times 39.9$

$ = 2523.675 = 2.52 \times {10^3}\;{\text{K}}$

As a result, the argon atom's temperature is  $2.52 \times {10^3}\;{\text{K}}$.

5 Marks Questions

1. Derive an expression for the pressure due to an ideal gas?

Ans: Consider an ideal gas confined in an OPRSTKL cubical container with capacity on each side a. ${\text{V}}$ now, ${\text{V}} = {{\text{a}}^3}$ ((Side) $^3 = $ volume of cube)

Where,  ${\text{n}} = $ Molecule of gas

${\text{m}} = $ Mass of each molecule

${\text{M}} = {\text{mxn}} = $ Mass of gas

Now Similarly, ${\text{Py}} = \dfrac{m}{{{a^3}}}\left( {y_1^2 + {y_2}^2 +  -  - {y_n}^2} \right)$

$Pz = \dfrac{m}{{{a^3}}}\left( {z_1^2 + {z_2}^2 +  -  - {z_n}^2} \right)$

${\text{P}} = $ Total pressure $ = \dfrac{{{P_x} + {P_y} + {P_z}}}{3}$

Put the following equation as per formula,

$ = \dfrac{1}{3}\left[ {\dfrac{m}{{{a^2}}}\left( {x_1^2 + x_2^2 +  -  - x_n^2} \right) + \dfrac{m}{{{a^2}}}\left( {y_1^2 + y_2^2 +  -  - y_n^2} \right) + \dfrac{m}{{{a^3}}}\left( {z_1^2 + z_2^2 +  -  - z_n^2} \right)} \right]$

${\text{P}} = \dfrac{m}{{3{a^3}}}\left[ {\left( {x_1^2 + y_1^2 + {z_1}^2} \right) +  -  -  - \left( {{x_n}^2 + {y_n}^2 + {z_n}^2} \right)} \right](\because $ from equation A)

$P = \dfrac{m}{{3v}}\left[ {C_1^2 + C_2^2 +  -  - C_n^2} \right]$

$ \to $ Multiply & divide by ${\text{n}}$ (no of molecules of gas)

$P = \dfrac{{1mpn}}{{3v}}\left[ {\dfrac{{C_1^2 + C_2^2 +  -  - {C_n}^2}}{n}} \right]$

${\text{P}} = \dfrac{{1{\text{M}}}}{{3v}}{C^2}$

${c^2} = \dfrac{{C_1^2 + C_2^2 +  -  - C_n^2}}{n}$ or $C = \sqrt {\dfrac{{C_1^2 + C_2^2 +  -  - C_n^2}}{n}} $

${\text{C}} = {\text{r}}.{\text{ms}}$. velocity of gas.

2: Figure 13.8 shows plot of $PV\mid T$ versus Poor $1.00 \times {10^{ - 3}}\;{\text{kg}}$ of oxygen gas at two different temperatures.

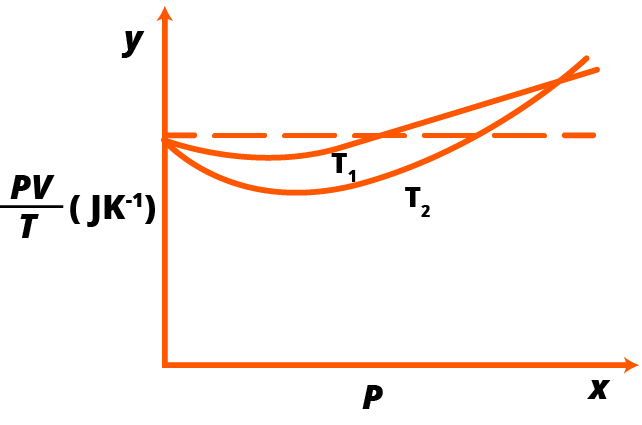
Molecular mass of ${H_2} = 2.02u,\,of\,O2 = 32.0{\text{u}},R = 8.31\;{\text{Jmo}}{1^{ - 1}}\;{{\text{K}}^{ - 1}}$

Ans: 

(a) What does the dotted plot signify?

The dotted plot in the graph, in which the ratio is equal, depicts the ideal behaviour of the gas Is a constant quality (where is the number of moles and is the universal gas constant). It isn't affected by the gas's pressure.

(b) Which is true: ${T_1} > {T_2}$ or ${T_1} < {T_2}?$

The dotted plot in the graph represents the ideal gas. The gas's temperature curve is closer to the dotted plot than the gas's temperature curve. When a real gas's temperature rises, it begins to behave like an ideal gas. As a result, is true for the given plot.

(c) What is the value of $PV/T$ where the curves meet on the $y$ -axis?

 The value of the ratio $PV/T$, where the two curves meet, is ${\mu _R}$. This is because the ideal gas equation is given as:

$PV = \mu RT$

$\dfrac{{PV}}{T} = \mu R$

Where,

$P$ is the pressure

$T$ is the temperature

$V$ is the volume

$\mu $ is the number of moles

$R$ is the universal constant

Molecular mass of oxygen $ = 32.0\;{\text{g}}$

Mass of oxygen $ = 1 \times {10^{ - 3}}\;{\text{kg}} = 1\;{\text{g}}$

We have, $R = 8.314\;{\text{J}}\;{\text{mol}}{{\text{e}}^{ - 1}}\;{{\text{K}}^{ - 1}}$

$\therefore \dfrac{{PV}}{T} = \dfrac{1}{{32}} \times 8.314$

$ = 0.26\;{\text{J}}{K^{ - 1}}$

Therefore, the value of the ratio $PV/T$, where the curves meet on the $y$ -axis, is

$0.26\;{\text{J}}{K^{ - 1}}$

(d) If we obtained similar plots for $1.00 \times {10^{ - 3}}\;{\text{kg}}$ of hydrogen, would we get the same value of $PV/T$ at the point where the curves meet on the $y$ -axis? If not, what mass of hydrogen yields the same value of $PV/T$ (for low pressure high temperature region of the plot)?  

If we obtain similar plots for $1.00 \times {10^{ - 3}}\;{\text{kg}}$ of hydrogen, then we will not get the same value of $PV/T$ at the point where the curves meet the $y$ -axis. This is because the molecular mass of hydrogen ( $(2.02{\text{u}})$ is different from that of oxygen (32.0 u).

We have:

$\dfrac{{PV}}{T} = 0.26J{K^{ - 1}}$

Now ,

$R = 8.314\;{\text{J}}\;{\text{mol}}{e^{ - 1}}\;{{\text{K}}^{ - 1}}$

Molecular mass $(M)$ of ${H_2} = 2.02{\text{u}}$

Let $\dfrac{{PV}}{T} = \mu R$ at constant temperature

where, $\mu  = \dfrac{m}{M}$

$m$ - Mass of ${H_2}$

$\therefore m = \dfrac{{PV}}{T} \times \dfrac{M}{R}$

$ = \dfrac{{0.26 \times 2.02}}{{8.31}}$

$ = 6.3 \times {10^{ - 2}}g = 6.3 \times {10^{ - 5}}\;{\text{kg}}$

Therefore,, $6.3 \times {10^{ - 5}}\;{\text{kg}}$ of ${H_2}$ will yield the same value of $PV/T$.

3: An oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm and a temperature of ${{27}^{0}}{\text{C}}$. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to ${{17}^{0}}{\text{C}}$. Estimate the mass of oxygen taken out of the cylinder $\left( {R = 8.31\;{\text{J}}\;{\text{mo}}{{\text{l}}^{ - 1}}\;{{\text{K}}^{ - 1}}} \right.$, molecular mass of ${{\text{O}}_2} = 32{\text{u}}$ ).

Ans: Given,

 Volume of oxygen, ${V_1} = 30$ litres - $30 \times {10^{ - 3}}\;{{\text{m}}^3}$

Gauge pressure, ${P_1} - 15\;{\text{atm}} = 15 \times 1.013 \times {10^5}\;{\text{Pa}}$

Temperature, ${T_1} = {{27}^{0}}{\text{C}} = 300\;{\text{K}}$

Universal gas constant, $R = 8.314\;{\text{J}}\;{\text{mo}}{{\text{l}}^{ - 1}}{{\mathbf{K}}^{ - 1}}$

Let the initial number of moles of oxygen gas in the cylinder be ${n_1}$.

Now we calculate the given equation,

${P_1}{V_1} = {n_1}R{T_1}$

$\therefore {n_1} = \dfrac{{{P_1}{V_1}}}{{R{T_1}}}$

$ = \dfrac{{15.195 \times {{10}^5} \times 30 \times {{10}^{ - 3}}}}{{(8.314) \times 300}} = 18.276$

But, ${n_1} = \dfrac{{{m_1}}}{M}$

Where,

${m_1} = $ Initial mass of oxygen

$M$ - Molecular mass of oxygen $ = 32\;{\text{g}}$

$\therefore {m_1} = {n_1}M = 18.276 \times 32 = 584.84\;{\text{g}}$

 The pressure and temperature drop after some oxygen is removed from the cylinder.

Given is , Volume, ${V_2} = 30$ litres $ = 30 \times {10^{ - 3}}\;{{\text{m}}^3}$

Gauge pressure, ${P_2} = 11\;{\text{atm}} = 11 \times 1.013 \times {10^5}\;{\text{Pa}}$

Temperature, ${T_2} = {{17}^{0}}{\text{C}} = 290\;{\text{K}}$

Let ${n_2}$ be the number of moles of oxygen left in the cylinder.

The gas equation is given as:

${P_2}{V_2} = {n_2}R{T_2}$

$\therefore {n_2} = \dfrac{{{P_2}{V_2}}}{{R{T_2}}}$

$ = \dfrac{{11.143 \times {{10}^5} \times 30 \times {{10}^{ - 3}}}}{{8.314 \times 290}} = 13.86$

But, ${n_2} = \dfrac{{{m_2}}}{M}$

Where,

${m_2}$ is the mass of oxygen remaining in the cylinder

$\therefore {m_2} = {n_2}M = 13.86 \times 32 = 453.1\;{\text{g}}$

The mass of oxygen taken out of the cylinder can be calculated using the following formula:

Mass of oxygen in the cylinder at the start - Mass of oxygen in the cylinder at the end$ = {m_1} - {m_2}$

$ = 584.84\;{\text{g}} - 453.1\;{\text{g}}$

$ = 131.74\;{\text{g}}$

$ = 0.131\;{\text{kg}}$

Hence, $0.131\;{\text{kg}}$ of oxygen is taken out of the cylinder.

4. Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at $2.0\;{\text{atm}}$ and temperature ${{17}^{0}}{\text{C}}$. Take the radius of a nitrogen molecule to be roughly $1.0_A^o$. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of $\left. {{{\text{N}}_2} = 28.0{\text{u}}} \right)$

Ans: We know that the , Mean free path $ = 1.11 \times {10^{ - 7}}\;{\text{m}}$

Collision frequency $ = 4.58 \times {10^9}\;{{\text{s}}^{ - 1}}$

Successive collision time $ \approx 500 \times $ (Collision time)

Pressure inside the cylinder containing nitrogen, $P = 2.0\;{\text{atm}} = 2.026 \times {10^5}\;{\text{Pa}}$

Let , Temperature inside the cylinder, $T = {}^ \circ {A^{{{17}^{0} }{\text{C}} - 290\;{\text{K}}}}$

Radius of a nitrogen molecule, $r = 1.0 - 1 \times {10^{10}}\;{\text{m}}$

Diameter, $d = 2 \times 1 \times {10^{10}} = 2 \times {10^{10}}\;{\text{m}}$

Molecular mass of nitrogen, $M = 28.0\;{\text{g}} = 28 \times {10^{ - 3}}\;{\text{kg}}$

The relationship gives the nitrogen root mean square speed :

${v_{n{\text{se}}}} = \sqrt {\dfrac{{3RT}}{M}} $

Where,

$R$ is the universal gas constant $ = 8.314\;{\text{J}}\;{\text{mol}}{{\text{e}}^{ - 1}}{K^{ - 1}}$

$\therefore {v_{me}} = \sqrt {\dfrac{{3 \times 8.314 \times 290}}{{28 \times {{10}^{ - 4}}}}}  = 508.26\;{\text{m}}/{\text{s}}$

The mean free path ( ${\text{b}}$ is given by the relation:

Now ,$l = \dfrac{{kT}}{{\sqrt 2  \times {d^2} \times P}}$

Where,

$K$ is the Boltzmann constant $ = 1.38 \times {10^{ - 21}}\;{\text{kg}}\;{{\text{m}}^2}\;{{\text{s}}^{ - 2}}\;{{\text{K}}^{ - 1}}$

$\therefore l = \dfrac{{1.38 \times {{10}^{ - 2}} \times 290}}{{\sqrt 2  \times 3.14 \times {{\left( {2 \times {{10}^{ - 12}}} \right)}^2} \times 2.026 \times {{10}^5}}}$

$ = 1.11 \times {10^{ - 7}}m$

Collision frequency $ = \dfrac{{{v_{rec}}}}{l}$

$ = \dfrac{{508.26}}{{1.11 \times {{10}^{ - 7}}}} = 4.58 \times 109{s^{ - 1}}$

Collision time is given as:

$T = \dfrac{d}{{{v_{nsL}}}}$

$ = \dfrac{{2 \times {{10}^{ - 10}}}}{{508.26}} = 3.93 \times {10^{ - 13}}s$

The amount of time that passes between subsequent collisions :

${T^\prime } = \dfrac{l}{{{v_{rm}}}}$

$ = \dfrac{{1.11 \times {{10}^{ - 7}}}}{{508.26\;{\text{m}}/{\text{s}}}} = 2.18 \times {10^{ - 10}}s$

$\therefore \dfrac{{{T^\prime }}}{T} = \dfrac{{2.18 \times {{10}^{ - 10}}}}{{3.93 \times {{10}^{ - 11}}}} = 500$

As a result, the period between subsequent collisions is 500 times that of a single collision.

5. A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres

${n_2} = {n_1}\exp \left[ { - mg\left( {{h_2} - {h_1}} \right)/{k_{\text{B}}}T} \right]$

Where $nl,{n_1}$ refer to number density at heights ${h_2}$ and ${h_1}$ respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid

Column:

${n_2} = {n_1}\exp \left[ { - mg{N_A}\left( {\rho  - {P^\prime }} \right)\left( {{h_2} - {h_1}} \right)/(\rho RT)} \right]$

Where $\rho $ is the density of the suspended particle, and ${\rho ^\prime }$ that of surrounding medium . I ${N_A}$ is  Avogadro's number, and $R$ the universal gas constant.] [Hint: use Archimedes principle to find the apparent

Ans:  We have, according to the rule of atmospheres,

${n_2} = {n_1}\exp \left[ { - mg\left( {{h_2} - {h_1}} \right)/{k_B}T} \right] \ldots (i)$

Where,

${n_1}$ is the number density at height ${h_1},and{n_2}$ is the number density at height ${h_2}$

${m_g}$ is the weight of the particle suspended in the gas column

Density of the medium $ = {\{{rho}^{0} }$

Density of the suspended particle $ = \rho $

Mass of one suspended particle $ = {{\mathbf{m}}^\prime }$

Mass of the medium displaced $ = m$

Volume of a suspended particle = $V$

The effective weight of a suspended particle in a liquid column is given by Archimedes' principle for a particle suspended in a liquid column as  :

Let  , Weight of the medium displaced - Weight of the suspended particle

$ = mg - {m^\prime }g$

$ = mg - V{\rho ^\prime }g = mg - \left( {\dfrac{m}{\rho }{\rho ^\prime }g} \right)$

$mg\left( {1 - \dfrac{{{\rho ^\prime }}}{\rho }} \right) -  \ldots  \ldots .(1i)$

Now Gas constant, ${\text{R}} = {k_B}\;{\text{N}}$

${k_B} = \dfrac{R}{N} \ldots (\omega i)$

Substituting equation (ii) in place of $m g$ in equation $(i)$ and then using equation (iii), we get:

${n_2} = {n_1}\exp \left[ { - mg\left( {{h_2} - {h_1}} \right)/{k_B}T} \right]$

$ - {n_1}\exp \left[ { - mg\left( {1 - \dfrac{{{\rho ^\prime }}}{\rho }} \right)\left( {{h_2} - {h_1}} \right)\dfrac{N}{{RT}}} \right]$

$ = {n_2}\exp \left[ { - mg\left( {\rho  - {\rho ^\prime }} \right)\left( {{h_2} - {h_1}} \right)\dfrac{N}{{RT\rho }}} \right]$

6. Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:

(Hint: Assume the atoms to be ‘tightly packed’ in a solid or liquid phase, and use the known value of Avogadro's number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few ${}^ \circ {A^{1.}}$.)

Ans:  Determine the atomic sizes in the range of a few Radius ${}^ \circ {A^{1.}}$.

Atomic mass of a substance $ = M$

Density of the substance $ = \rho $

Avogadro's number $ = {\text{N}} = 6.023 \times {10^2}$

Volume of each atom $ = \dfrac{4}{3}\pi {r^3}$

Volume of $N$ number of molecules $ = \dfrac{4}{3}\pi {r^3}N \ldots (i)$

volume of one mole of a substance $ = \dfrac{M}{\rho } \ldots (ii)$

$ = \dfrac{4}{3}\pi {r^3}$

$N = \dfrac{M}{\rho }$

$\therefore r = \sqrt[3]{{\dfrac{{3.M}}{{4\pi \rho N}}}}$

For carbon:

$M = 12.01 \times {10^{ - 3}}\;{\text{kg}}$

$\rho  = 2.22 \times {10^3}\;{\text{kg}}\;{{\text{m}}^{ - 3}}$

$\therefore r = {\left( {\dfrac{{3 \times 12.1 \times {{10}^{ - 4}}}}{{4\pi  \times 2.22 \times {{10}^9} \times 6.023 \times {{10}^2}}}} \right)^{\dfrac{1}{3}}} = 1.29\dot A$

As a result, a carbon atom's radius is 1.29 A.

For the sake of gold:

$M - 197.00 \times {10^{ - 1}}\;{\text{kg}}$

$\rho  = 19.32 \times {10^3}\;{\text{kg}}\;{{\text{m}}^{ - 3}}$

$\therefore r = {\left( {\dfrac{{3 \times 197 \times {{10}^{ - 1}}}}{{4\pi  \times 19.32 \times {{10}^3} \times 6.023 \times {{10}^2}}}} \right)^{\dfrac{1}{3}}} = 1.59{}^ \circ A$

As a result, a gold atom's radius is 1.59.

In the case of liquid nitrogen:

$M = 14.01 \times {10^{ - 1}}\;{\text{kg}}$

$\rho  = 1.00 \times {10^3}\;{\text{kg}}\;{{\text{m}}^{ - 1}}$

$\therefore r = {\left( {\dfrac{{3 \times 14.01 \times {{10}^{ - 1}}}}{{4\pi  \times 1.00 \times {{10}^3} \times 6.23 \times {{10}^{21}}}}} \right)^{\dfrac{1}{3}}} = {{1.77}^{0} }A$

As a result, a liquid nitrogen atom's radius is 1.77 ${A}^{0}$ .

In the case of lithium:

$M = 6.94 \times {10^{ - 1}}\;{\text{kg}}$

${\text{p}} = 0.53 \times {10^{\text{i}}}{\text{kg}}{{\text{m}}^{ - 3}}$

$\therefore r = {\left( {\dfrac{{3 \times 6.94 \times {{10}^{ - 3}}}}{{4\pi  \times 0.53 \times {{10}^1} \times 6.23 \times {{10}^{41}}}}} \right)^{\dfrac{1}{3}}} - 1.73{}^ \circ A$

As a result, the radius of a lithium atom is – 1.73 ${A}^{0}$ For liquid fluorine, the radius of a lithium atom is :

$M = 19.00 \times {10^{ - 3}}\;{\text{kg}}$

$\rho  = 1.14 \times {10^3}kg$

Important Related Links for CBSE Class 11