Motion in a Plane Class 11 important questions with answers PDF download
NCERT Solutions for Motion in a Plane Class 11 Physics is provided in the form of a free PDF as this chapter is very important from the examination point of view. It would benefit the students to prepare for their assessments. Chapter 3 Physics Class 11 NCERT Solutions have been prepared to keep in mind the latest syllabus prescribed by the CBSE. These solutions are prepared by skilled teachers who have been teaching for years and are very well accustomed to the syllabus and scoring schemes.
CBSE Class 11 Physics Important Questions would help the student obtain a better knowledge of the subject. We have added a free PDF to download so that the students can study the notes from anywhere and at any time. The study includes important concepts discussed and tips on how to utilize the NCERT Solutions for Motion in a Plane in the study curriculum of a student.
Study Important Questions for Class 11 Physics Chapter 3 – Motion in A Plane
1 Mark Questions
1. What is the trajectory of a projectile?
Ans: Trajectory of a projectile can be defined as the path followed by a projectile. The trajectory may be of various forms, for example, parabola.
2. A projectile is fired at an angle of \[{{30}^{\circ }}\] with the horizontal with velocity \[10m/s\]. At what angle with the vertical should it be fired to get maximum range?
Ans: The maximum range that can be achieved is at an angle of \[{{45}^{\circ }}\].
3. What is the value of angular speed for 1 revolution?
Ans: For one complete revolution, \[\theta =2\pi \] in time period \[t=T\], the angular speed can be given as \[\omega =\frac{2\pi }{T}\].
4. Give an example of a body moving with uniform speed but having a variable velocity and an acceleration which remains constant in magnitude but changes in direction
Ans: An example of a body moving with uniform speed having velocity that is not constant can be given as a body moving in a circular path.
5. What is the direction of centripetal force when particle is following a circular path?
Ans: The direction of the centripetal force in a circular path is towards the centre of the circle.
6. Two vectors \[\vec{A}\] and \[\vec{B}\] are perpendicular to each other. What is the value of \[\vec{A}\cdot \vec{B}\]?
Ans: We know, \[\theta ={{90}^{\circ }}\]
\[\vec{A}\cdot \vec{B}=AB\cos \theta \]
\[\Rightarrow \vec{A}\cdot \vec{B}=0\]
7. What will be the effect on horizontal range of a projectile when its initial velocity is doubled, keeping the angle of projection same?
Ans: The horizontal range will be four times the initial horizontal range.
8. What will be the effect on the maximum height of a projectile when its angle of projection is changed from \[{{30}^{\circ }}\]to \[{{60}^{\circ }}\], keeping the same initial velocity of projection?
Ans: The maximum height will be three times the initial vertical height.
9. What is the angular velocity of the hour hand of a clock?
Ans: The angular velocity is \[\frac{\pi }{6}radian\,per\,hour\].
10. A body is moving on a curved path with a constant speed. What is the nature of its acceleration?
Ans: Acceleration should be perpendicular to the direction of motion and nature is called as centripetal acceleration.
11. State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
Ans: Scalars: Volume, mass, density, speed, number of moles, angular frequency
Vectors: Acceleration, displacement, velocity, angular velocity
A scalar quantity is expressed by its magnitude only. It does not have any direction related with it. Volume, mass, speed, density, number of moles, and angular frequency are some of the scalar physical quantities.
On the other hand, a vector quantity is specified by its magnitude as well as the direction associated with it.
Acceleration, velocity, displacement, and angular velocity come under this category.
12. Pick out the two scalar quantities in the following list:
force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.
Ans: Work and current are scalar quantities.
Work done is expressed by the dot product of force and displacement. Because the dot product of two quantities is always a scalar, work is a scalar physical quantity.
Current is expressed only by its magnitude. Its direction is not taken into consideration. Therefore, it is a scalar quantity.
13. Pick out the only vector quantity in the following list:
Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.
Ans: Impulse is a vector quantity.
Impulse is expressed as the product of force and time. Because the force is a vector quantity, its product with time (a scalar quantity) gives a vector quantity.
2 Marks Questions
1. What is the angle between two forces of \[2N\] and \[3N\] having resultant as \[4N\]?
Ans: Using the equation \[R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\]
We can write,
\[\Rightarrow 4=\sqrt{{{2}^{2}}+{{3}^{2}}+2\times 2\times 3\cos \theta }\]
\[\Rightarrow 16=4+9+12\cos \theta \]
\[\Rightarrow \cos \theta =\frac{3}{12}={{\cos }^{-1}}0.25\]
\[\Rightarrow \theta =75{}^\circ 32'\], which is the required angle.
2. What is the angle of projection at which horizontal range and maximum height are equal?
Ans: We can write,
\[\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\]
\[\because \frac{{{u}^{2}}\sin 2\theta }{g}=R\,\left( Horizontal\,Range \right)\]
Therefore, we can write,
\[\sin 2\theta =\frac{1}{2}{{\sin }^{2}}\theta \]
\[\because \frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}={{H}_{\max }}\left( Maximum\,Height \right)\]
\[\Rightarrow 2\sin \theta \cos \theta =\frac{1}{2}{{\sin }^{2}}\theta \]
\[\Rightarrow \tan \theta =4\]
\[\Rightarrow \theta =75.96{}^\circ \], which is the required angle of projection.
3. Prove that for elevations that exceed or fall short of \[45{}^\circ \] by equal amounts the ranges are equal.
Ans: We know that,
\[R=\frac{{{u}^{2}}\sin 2\theta }{g}\]
And,
\[{{\theta }_{1}}=45{}^\circ +\alpha \]
\[{{\theta }_{2}}=45{}^\circ -\alpha \]
\[{{R}_{1}}=\frac{{{u}^{2}}\sin 2{{\theta }_{1}}}{g}=\frac{{{u}^{2}}\sin 2\left( 45{}^\circ +\alpha \right)}{g}\]
\[\Rightarrow {{R}_{1}}=\frac{{{u}^{2}}\sin \left( 90{}^\circ +2\alpha \right)}{g}\]
And,
\[{{R}_{2}}=\frac{{{u}^{2}}\sin 2{{\theta }_{2}}}{g}=\frac{{{u}^{2}}\sin 2\left( 45{}^\circ -\alpha \right)}{g}\]
\[\Rightarrow {{R}_{2}}=\frac{{{u}^{2}}\sin \left( 90{}^\circ -2\alpha \right)}{g}\]
Therefore, we can write, \[{{R}_{1}}={{R}_{2}}\].
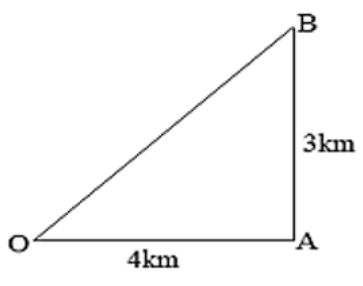
4. At what range will a radar set show a fighter plane flying at \[3km\] above its centre and at a distance of \[4km\] from it?
Ans: Here, the straight distance of the object from the radar can be given as \[=OB\]
\[OB=\sqrt{{{4}^{2}}+{{3}^{2}}}\]
\[\Rightarrow OB=\sqrt{16+9}\]
\[\Rightarrow OB=\sqrt{25}\]
\[\Rightarrow OB=5\]
\[\Rightarrow Range=5km\]
5. Two forces \[5kg\,wt\] and \[10kg\,wt\] are acting with an inclination of \[120{}^\circ \] between them. What is the angle which the resultant makes with \[10kg\,wt\]?
Ans: We can write,
\[{{F}_{1}}=5kg\,wt\]
\[{{F}_{2}}=10kg\,wt\]
\[\Rightarrow F=\sqrt{{{F}_{1}}^{2}+{{F}_{2}}^{2}+2{{F}_{1}}{{F}_{2}}\cos \theta }\]
\[\tan \beta =\frac{{{F}_{2}}\sin \theta }{{{F}_{1}}+{{F}_{2}}\cos \theta }\]
\[\Rightarrow \tan \beta =\frac{5\sin 120{}^\circ }{10+5\cos 120{}^\circ }\]
\[\Rightarrow \tan \beta =\frac{5\times \frac{\sqrt{3}}{2}}{10-5\times \frac{1}{2}}\]
\[\Rightarrow \tan \beta =\frac{1}{\sqrt{3}}\]
\[\Rightarrow \beta ={{\tan }^{-1}}\left( \frac{1}{\sqrt{3}} \right)=30{}^\circ \], which is the required angle here.
6. A stone is thrown vertically upwards and then it returns to the thrower. Is it a projectile? Explain.
Ans: A stone thrown vertically upwards cannot be called as a projectile since a projectile must have two perpendicular components of velocities but in the given case a stone has velocity in one direction while going up or coming downwards.
7. Which is greater: the angular velocity of the hour hand of a watch or angular velocity of the earth around its own axis?
Ans: In hour hand of a watch time period can be given as \[T=\frac{1}{2}h\]
\[{{\omega }_{H}}=\frac{2\pi }{12}\]
For rotation of earth can be given as \[T\text{ }=24h\]
\[{{\omega }_{E}}=\frac{2\pi }{24}\]
\[\Rightarrow \frac{{{\omega }_{H}}}{{{\omega }_{E}}}=\frac{24}{12}=2\]
\[\Rightarrow {{\omega }_{H}}=2{{\omega }_{E}}\]
Clearly, \[{{\omega }_{H}}>{{\omega }_{E}}\].
8. Why does the direction of motion of a projectile become horizontal at the highest point of its trajectory?
Ans: At the highest point of the trajectory, the vertical component of velocity becomes zero. Thus, the direction of motion of the projectile becomes horizontal.
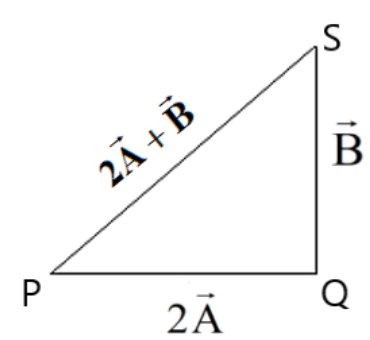
9. A vector \[\vec{A}\] has magnitude 2 and another vector \[\vec{B}\] have magnitude 3 and is perpendicular to each other. By vector diagram, find the magnitude of \[2\vec{A}+\vec{B}\] and show its direction in the diagram.
Ans: We can write,
\[\overrightarrow{PQ}=2\vec{A}=4cm;\overrightarrow{QS}=\vec{B}=3cm\]
\[\left| \overrightarrow{PS} \right|=\sqrt{P{{Q}^{2}}+Q{{S}^{2}}}\Rightarrow \left| \overrightarrow{PS} \right|=\sqrt{{{4}^{2}}+{{3}^{2}}}\Rightarrow \left| \overrightarrow{PS} \right|=5cm\]
10. Find a unit vector parallel to the resultant of the vectors \[\vec{A}=2\hat{i}+3\hat{j}+4\hat{k}\] and \[\vec{B}=3\hat{i}+5\hat{j}+\hat{k}\].
Ans: We know that \[\hat{R}=\frac{{\vec{R}}}{\left| {\vec{R}} \right|}\]
\[\vec{R}=\vec{A}+\vec{B}=\left( 2\hat{i}+3\hat{j}+4\hat{k} \right)+\left( 3\hat{i}+5\hat{j}+\hat{k} \right)\]
\[\Rightarrow \vec{R}=5\hat{i}-2\hat{j}+5\hat{k}\]
\[\Rightarrow \left| {\vec{R}} \right|=\sqrt{{{5}^{2}}+{{\left( -2 \right)}^{2}}+{{5}^{2}}}\]
\[\Rightarrow \left| {\vec{R}} \right|=\sqrt{25+4+25}\]
\[\Rightarrow \left| {\vec{R}} \right|=\sqrt{54}\]
\[\Rightarrow \hat{R}=\frac{5\hat{i}-2\hat{j}+5\hat{k}}{\sqrt{54}}\], which is the required unit vector.
11. A stone tied at the end of string is whirled in a circle. If the string breaks, the stone flies away tangentially. Why?
Ans: When a stone, that is tied at the endpoint of a string, moving around a circular path, its velocity acts tangent to the circle.
When the string breaks, the centripetal force will not act. Because of inertia, the stone continues to move along the tangent to the circular path and flies off tangentially to the circular path.
12. What are the two angles of projection of a projectile projected with velocity \[30m/s\], so that the horizontal range is \[45m\]. Take, \[g=10m/{{s}^{2}}\].
Ans: We can write,
\[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{30}^{2}}\times \sin 2\theta }{10}=45\]
\[\Rightarrow \sin 2\theta =\frac{450}{{{30}^{2}}}\]
\[\Rightarrow \sin 2\theta =\frac{1}{2}\]
\[2\theta =30{}^\circ \,or\,150{}^\circ \]
\[\Rightarrow \theta =15{}^\circ \,or\,75{}^\circ \], which are the two required angles of projection.
13. The blades of an aeroplane propeller are rotating at the rate of \[600\]revolutions per minute. Calculate its angular velocity.
Ans: We can write,
\[\nu =600\,rev/\min \]
\[\Rightarrow \nu =\frac{600}{60}rev/\sec \]
\[\omega =2\pi \nu =2\pi \times \frac{600}{60}\]
\[\Rightarrow \omega =20\pi rad/\sec \], which is the required angular velocity.
14. What is a uniform circular motion? Explain the terms time period, frequency and angular velocity. Establish a relation between them.
Ans: When an object moves in a circular path with constant speed then the motion is said to be a uniform circular motion
The time period can be defined as the time taken by the object to complete one revolution
Frequency can be given as the total number of revolutions in one second.
Angular velocity can be stated as the time rate of change of angular displacement.
\[\omega =\frac{2\pi }{T}=2\pi \nu \]
\[\Rightarrow \frac{1}{T}=\nu \], which is the required relation.
15. A body of mass \[m\]is thrown with velocity\[v\] at angle of \[30{}^\circ \]to the horizontal and another body B of the same mass is thrown with velocity at an angle of \[{{60}^{\circ }}\] to the horizontal. Find the ratio of the horizontal range and maximum height of A and B?
Ans:
Case 1:
When \[\theta ={{30}^{\circ }}\]
\[{{R}_{A}}=\frac{{{u}^{2}}}{g}\times \sin 2\left( {{30}^{\circ }} \right)\]
\[\Rightarrow {{R}_{A}}=\frac{{{u}^{2}}}{g}\times \frac{\sqrt{3}}{2}\]
When \[\theta ={{60}^{\circ }}\]
\[{{R}_{B}}=\frac{{{u}^{2}}}{g}\times \sin 2\left( {{60}^{\circ }} \right)\Rightarrow {{R}_{B}}=\frac{{{u}^{2}}}{g}\times \frac{\sqrt{3}}{2}\Rightarrow {{R}_{A}}:{{R}_{B}}=1:1\]
Case 2:
When \[\theta ={{30}^{\circ }}\]
\[{{H}_{A}}=\frac{{{u}^{2}}}{g}\times {{\sin }^{2}}{{30}^{\circ }}\Rightarrow {{H}_{A}}=\frac{{{u}^{2}}}{g}\left( \frac{1}{4} \right)\]
When \[\theta ={{60}^{\circ }}\]
\[{{H}_{B}}=\frac{{{u}^{2}}}{g}\times {{\sin }^{2}}{{60}^{\circ }}\Rightarrow {{H}_{B}}=\frac{{{u}^{2}}}{g}\left( \frac{3}{4} \right)\Rightarrow {{H}_{A}}:{{H}_{B}}=1:3\], which is the required ratio.
16. Read each statement below carefully and state with reasons, if it is true or false:
a) The magnitude of a vector is always a scalar.
Ans: True.
The magnitude of a vector is a number. Therefore, it is a scalar.
b) Each component of a vector is always a scalar.
Ans: False.
Each component of a vector is also a vector.
c) The total path length is always equal to the magnitude of the displacement vector of a particle.
Ans: False.
Total path length is a scalar quantity, whereas displacement is a vector quantity. Therefore, the total path length is always greater than the magnitude of displacement. It becomes equal to the magnitude of displacement only when a particle is moving in a straight line.
d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time.
Ans: True.
It is because of the fact that the total path length is always greater than or equal to the magnitude of displacement of a particle.
e) Three vectors not lying in a plane can never add up to give a null vector.
Ans: True.
Three vectors, which do not lie in a plane, cannot be represented by the sides of a triangle taken in the same order.
17. State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
a) Adding any two scalars
Ans: Meaningful.
The addition of two scalar quantities is meaningful only if they both represent the same physical quantity.
b) Adding a scalar to a vector of the same dimensions.
Ans: Not meaningful.
The addition of a vector quantity with a scalar quantity is not meaningful.
c) Multiplying any vector by any scalar.
Ans: Meaningful.
A scalar can be multiplied with a vector. For example, force is multiplied with time to give impulse.
d) Multiplying any two scalars.
Ans: Meaningful.
A scalar, irrespective of the physical quantity it represents, can be multiplied with another scalar having the same or different dimensions.
e) Adding any two vectors.
Ans: Meaningful.
The addition of two vector quantities is meaningful only if they both represent the same physical quantity.
f) Adding a component of a vector to the same vector.
Ans: Meaningful.
A component of a vector can be added to the same vector as they both have the same dimensions.
18. Three girls skating on a circular ice ground of radius \[200m\] start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in Fig. 4.20. What is the magnitude of the displacement vector for each? For which girl is this equal to the actual length of the path skated?
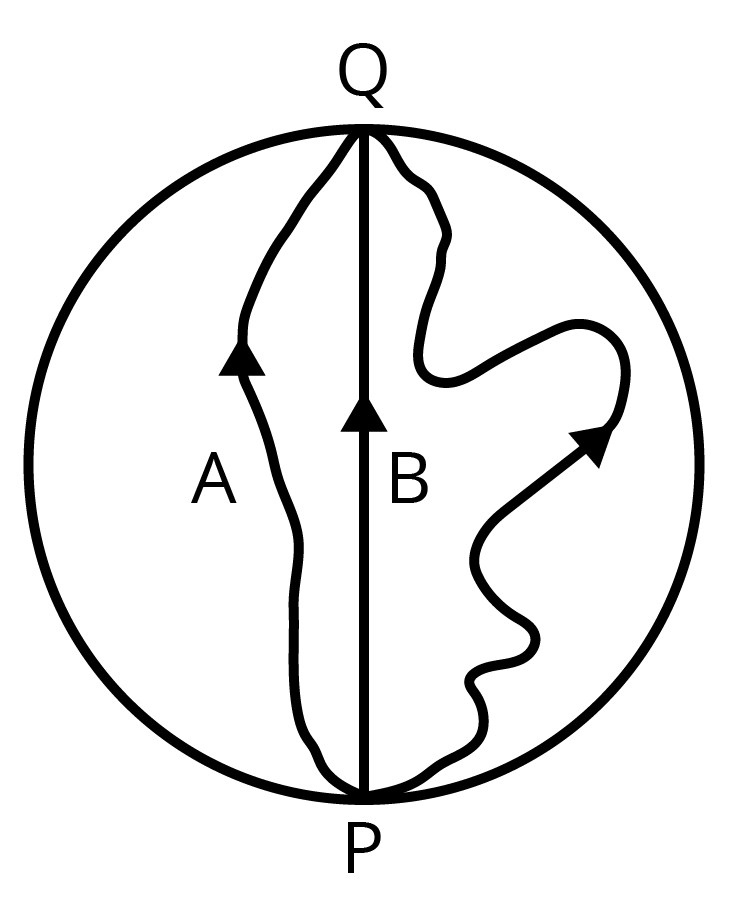
Ans: Displacement can be given by the minimum distance between the initial and final positions of a particle. In the given case, all the girls start from point P and reach point Q. The magnitudes of their displacements will be equal to the diameter of the ground.
Radius of the ground can be given as\[=200m\]
Diameter of the ground \[=2\times 200=400m\]
Therefore, the magnitude of the displacement for each girl is \[400m\]. This is equal to the actual length of the path skated by girl B.
19. A man can swim with a speed of \[4.0km/h\] in still water. How long does he take to cross a river \[1km\] wide if the river flows steadily at \[3.0km/h\]and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?
Ans: Speed of the man is given as \[{{v}_{m}}=4.0km/h\]
Width of the river is given as \[1km\]
$Time\,taken\,to\,cross\,the\,river=\frac{Width\,of\,the\,river}{Speed\,of\,the\,river} $
$\Rightarrow Time\,taken\,to\,cross\,the\,river=\frac{1}{4}h=\frac{1}{4}\times 60=15\min$
Speed of the river, \[{{v}_{r}}=3km/h\]
Distance covered with flow of the river \[={{v}_{r}}\times t\]
\[\Rightarrow 3\times \frac{1}{4}=\frac{3}{4}\Rightarrow \frac{3}{4}\times 1000=750m\], which is the required distance.
20. A stone tied to the end of a string \[80cm\]long is whirled in a horizontal circle with a constant speed. If the stone makes \[14\]revolutions in \[25s\], what is the magnitude and direction of acceleration of the stone?
Ans: Length of the string is given as, \[l=80cm=0.8m\]
Number of revolutions \[=14\]
Time taken \[=25s\]
Frequency, \[\nu =\frac{No.\,of\,revolutions}{Time\,taken}=\frac{14}{25}Hz\]
Angular frequency can be given as, \[\omega =2\pi \nu \]
\[\Rightarrow \omega =2\times \frac{22}{7}\times \frac{14}{25}=\frac{88}{25}rad/s\]
Centripetal acceleration can be given as,
\[{{a}_{c}}={{\omega }^{2}}r\Rightarrow {{a}_{c}}={{\left( \frac{88}{25} \right)}^{2}}\times 0.8\Rightarrow {{a}_{c}}=9.91m/{{s}^{2}}\]
The direction of centripetal acceleration is directed along the string, toward the centre, at all points.
21. An aircraft executes a horizontal loop of radius \[1.0km\] with a steady speed of \[900km/h\]. Compare its centripetal acceleration with the acceleration due to gravity.
Ans: Given that,
Radius of the loop is given as, \[r=1.0km=1000m\]
Speed of the aircraft is given as, \[v=900km/h\]
Centripetal acceleration,
\[{{a}_{c}}=\frac{{{v}^{2}}}{r}\Rightarrow {{a}_{c}}=\frac{{{\left( 250 \right)}^{2}}}{1000}=62.5m/{{s}^{2}}\]
Acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
\[\Rightarrow \frac{{{a}_{c}}}{g}=\frac{62.5}{9.8}=6.38\Rightarrow {{a}_{c}}=6.38g\], which is the required relation.
22. Read each statement below carefully and state, with reasons, if it is true or false:
a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre
Ans: False.
The net acceleration of a particle in circular motion is not always directed along the radius of the circle toward the centre. It happens only in the case of uniform circular motion.
b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point
Ans: True.
At a point on a circular path, a particle appears to move tangentially to the circular path on which it is moving.
Therefore, the velocity vector of the particle is always along the tangent at a point.
c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector
Ans: True.
In uniform circular motion (UCM), the direction of the acceleration vector points toward the centre of the circle. But it constantly changes with time. The average of these vectors over one cycle is a null vector.
23. A cricketer can throw a ball to a maximum horizontal distance of \[100m\]. How much high above the ground can the cricketer throw the same ball?
Ans: Maximum horizontal distance can be given as, \[R=100m\]
It will be possible for the cricketer to throw the ball to the maximum horizontal distance when the angle of projection is \[45{}^\circ \], i.e., \[\theta =45{}^\circ \].
The horizontal range for a projection velocity \[v\], can be expressed by the relation:
\[R=\frac{{{u}^{2}}\sin 2\theta }{g}\]\[\Rightarrow 100=\frac{{{u}^{2}}\sin {{90}^{\circ }}}{g}\Rightarrow \frac{{{u}^{2}}}{g}=100\]
The ball will achieve the maximum height when it is thrown vertically upward. For such motion, the final velocity v is zero at the maximum height H.
Acceleration is given as, \[a=-g\]
Using the third equation of motion:
\[{{v}^{2}}-{{u}^{2}}=-2gH\]
\[\Rightarrow H=\frac{1}{2}\times \frac{{{u}^{2}}}{g}=\frac{1}{2}\times 100=50m\], which is the required height.
24. The position of a particle is given by \[r=\left( 3t\hat{i}-2{{t}^{2}}\hat{j}+4\hat{k} \right)m\]where \[t\] is in seconds and the coefficients have the proper units for \[r\] to be in metres.
a) Find the \[v\] and \[a\] of the particle.
Ans: The position of the particle is given by: \[\vec{r}=3t\hat{i}-2{{t}^{2}}\hat{j}+4\hat{k}\]
Velocity \[\vec{v}\], of the particle is given as:
\[\vec{v}=\frac{d\vec{r}}{dt}=\frac{d}{dt}\left( 3t\hat{i}-2{{t}^{2}}\hat{j}+4\hat{k} \right)\Rightarrow \vec{v}=3\hat{i}-4t\hat{j}\]
Acceleration \[\vec{a}\], of the particle is given as:
\[\vec{a}=\frac{d\vec{v}}{dt}=\frac{d}{dt}\left( 3\hat{i}-4t\hat{j} \right)\Rightarrow \vec{a}=-4\hat{j}\]
b) What is the magnitude and direction of velocity of the particle at \[t=2.0s\] ?
Ans: We have velocity vector as, \[\vec{v}=3\hat{i}-4t\hat{j}\]
At \[t=2.0s\],
\[\vec{v}=3\hat{i}-8\hat{j}\]
The magnitude of velocity is given by:
\[\left| {\vec{v}} \right|=\sqrt{{{3}^{2}}+{{\left( -8 \right)}^{2}}}=\sqrt{73}=8.54m/s\]
Direction can be given as,
\[\theta ={{\tan }^{-1}}\left( \frac{{{v}_{y}}}{{{v}_{x}}} \right)\Rightarrow \theta ={{\tan }^{-1}}\left( \frac{-8}{3} \right)={{\tan }^{-1}}\left( 2.667 \right)=-69.45{}^\circ \]
The negative sign indicates that the direction of velocity is below the x-axis.
25. For any arbitrary motion in space, which of the following relations are true:
(The ‘average’ stands for average of the quantity over the time interval \[{{t}_{1}}\] to \[{{t}_{2}}\])
a) \[{{v}_{average}}=\left( \frac{1}{2} \right)\left( v\left( {{t}_{1}} \right)+v\left( {{t}_{2}} \right) \right)\]
Ans: False.
It is given that the motion of the particle is arbitrary. Therefore, the average velocity of the particle cannot be given by this equation.
b) \[{{v}_{average}}=\frac{\left[ r\left( {{t}_{2}} \right)-r\left( {{t}_{1}} \right) \right]}{\left( {{t}_{2}}-{{t}_{1}} \right)}\]
Ans: True.
The arbitrary motion of the particle can be represented by this equation.
c) \[v\left( t \right)=v\left( 0 \right)+at\]
Ans: False.
The motion of the particle is arbitrary. The acceleration of the particle may also be non-uniform. Therefore, this equation cannot represent the motion of the particle in space.
d) \[r\left( t \right)=r\left( 0 \right)+v\left( 0 \right)t+\frac{1}{2}a{{t}^{2}}\]
Ans: False.
The motion of the particle is arbitrary; acceleration of the particle may also be non-uniform. Therefore, this equation cannot represent the motion of particle in space.
e) \[{{a}_{average}}=\frac{\left[ v\left( {{t}_{2}} \right)-v\left( {{t}_{1}} \right) \right]}{\left( {{t}_{2}}-{{t}_{1}} \right)}\]
Ans: True.
The arbitrary motion of the particle can be represented by this equation.
26. Read each statement below carefully and state, with reasons and examples, if it is true or false:
A scalar quantity is one that
a) is conserved in a process
Ans: False.
Nevertheless, being a scalar quantity, energy is not conserved in inelastic collisions.
b) can never take negative values
Ans: False.
Despite being a scalar quantity, the temperature can take negative values.
c) must be dimensionless
Ans: False.
The total path length is a scalar quantity. Yet it has the dimension of length.
d) does not vary from one point to another in space
Ans: False.
A scalar quantity such as gravitational potential can vary from one point to another in space.
e) has the same value for observers with different orientations of axes
Ans: True.
The value of a scalar does not vary for observers with different orientations of axes.
27.
a) A vector has magnitude and direction. Does it have a location in space?
Ans: No.
Generally, a vector has no definite locations in space. This is due to a vector
remains invariant when displaced in such a way that its magnitude and direction remain the same. However, a position vector has a definite location in space.
b) Can it vary with time?
Ans: Yes.
A vector can vary with time. Example can be given as, the displacement vector of a particle moving with a certain velocity varies with time.
c) Will two equal vectors a and b at different locations in space necessarily have identical physical effects? Give examples in support of your answer.
Ans: No.
Two equal vectors located at different locations in space need not produce the same physical effect. For example, two equal forces that are acting on an object at different points can cause the body to rotate, but their combination cannot produce an equal turning effect.
28.
a) A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector?
Ans: No.
A physical quantity having both magnitude and direction need not be always considered a vector.
For example, despite having magnitude and direction, current is a scalar quantity. The essential requirement for a physical quantity to be considered a vector is that it should follow the law of vector addition.
b) The rotation of a body can be specified by the direction of the axis of rotation, and the angle of rotation about the axis. Does that make any rotation a vector?
Ans: No.
Generally, the rotation of a body about an axis is not a vector quantity as it does not follow the law of vector addition. But a rotation by a certain small angle follows the law of vector addition and is therefore considered a vector.
29. Can you associate vectors with
a) The length of a wire bent into a loop?
Ans: No.
One cannot relate a vector with the length of a wire bent into a loop.
b) A plane area?
Ans: Yes.
One can relate an area vector with a plane area. The direction of this vector is normal, inward, or outward to the plane area.
c) A sphere?
Ans: No.
One cannot relate a vector with the volume of a sphere. However, an area vector can be related with the area of a sphere.
3 Marks Questions
1. Derive expressions for velocity and acceleration for uniform circular motion.
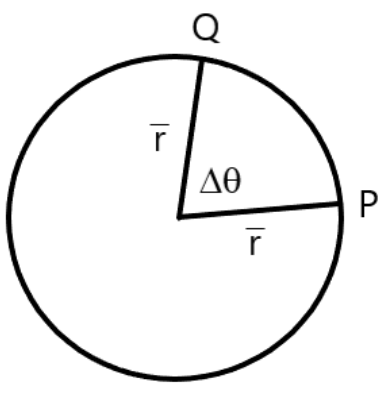
Ans: We can write,
If \[PQ=\Delta l\],
\[V=\frac{\Delta l}{\Delta t}\]
And angular velocity can be given as \[\omega =\frac{\Delta \theta }{\Delta l}\]
Using \[\theta =\frac{l}{r}\Rightarrow \Delta \theta =\frac{\Delta l}{r}\]…… (1)
\[\Delta l=V\Delta t\] and \[\Delta \theta =\omega \Delta t\]
Substituting in (1)
\[\omega \Delta t=V\frac{\Delta t}{r}\]
\[\Rightarrow V=r\omega \], which is the required expression for velocity.
Also,
\[a=\frac{dV}{dt}=r\frac{d\omega }{dt}=\omega \frac{dr}{dt}=\omega V=\frac{V}{r}\times V=\frac{{{V}^{2}}}{r}\]
\[\Rightarrow a=\frac{{{V}^{2}}}{r}\], which is the required expression for acceleration.
2. Derive an equation for the path of a projectile fired parallel to horizontal.
Ans: Let a projectile having initial uniform horizontal velocity u be under the influence of gravity, then at any instant t at position P the horizontal and vertical.
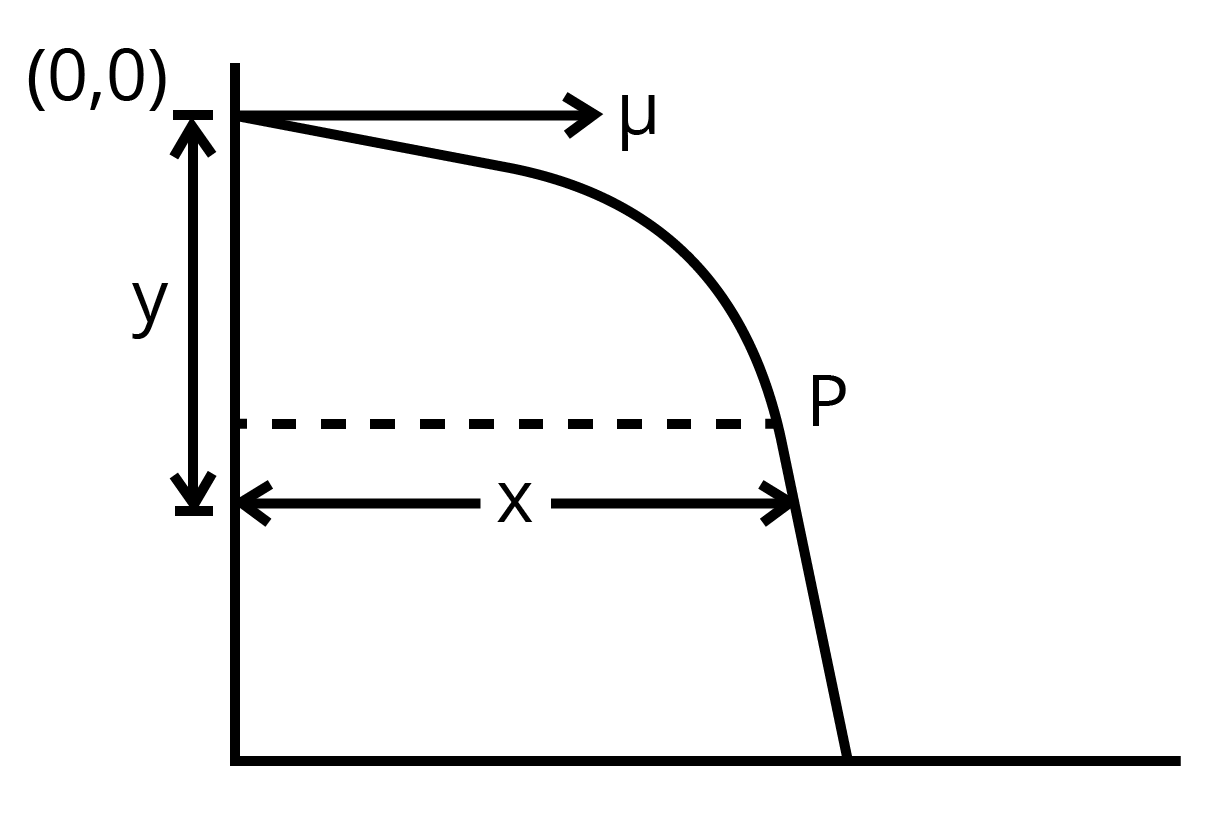
For horizontal motion
\[s=ut+\frac{1}{2}a{{t}^{2}}\]
\[s=x\], \[u=u\], \[t=t\], \[a=0\]
\[x=ut\]
\[\Rightarrow t=\frac{x}{u}\] …… (1)
For vertical motion,
\[s=ut+\frac{1}{2}a{{t}^{2}}\]
\[s=-y\], \[u=0\], \[t=t\], \[a=-g\]
\[-y=-\frac{1}{2}g{{t}^{2}}\]
\[\Rightarrow y=\frac{1}{2}g{{t}^{2}}\] …… (2)
Using equation (1) and (2)
\[\Rightarrow y=\frac{1}{2}g{{\left( \frac{x}{u} \right)}^{2}}=\frac{1}{2}g\frac{{{x}^{2}}}{{{u}^{2}}}\], which is the required equation of the path.
3.
a) Define time of flight and horizontal range.
Ans: The time taken by the projectile to complete its trajectory is defined as time of flight.
The maximum horizontal distance covered by the projectile from the foot of the tower to the point where projectile hits the ground is defined as horizontal range.
b) From a certain height above the ground a stone A is dropped gently. Simultaneously another stone B is fired horizontally. Which of the two stones will arrive on the ground earlier?
Ans: Both the stones will reach the ground simultaneously since the initial vertical velocity in both cases is zero and both are falling with same acceleration equal to acceleration due to gravity.
4. At what point of projectile motion
a) Potential energy is the maximum?
Ans: P.E. will be maximum at the highest point(H).
\[{{\left( P.E. \right)}_{Highest\,Point}}=mgH\]
\[\Rightarrow {{\left( P.E. \right)}_{H}}=mg\left( \frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g} \right)\Rightarrow {{\left( P.E. \right)}_{H}}=\frac{1}{2}m{{u}^{2}}{{\sin }^{2}}\theta \]
b) Kinetic energy is the minimum?
Ans: K.E will be minimum at the highest point. i.e.,
\[{{\left( K.E. \right)}_{H}}=\frac{1}{2}m{{\left( {{v}_{H}} \right)}^{2}}\]
Here, vertical component of velocity is zero.
\[\Rightarrow {{\left( K.E. \right)}_{H}}=\frac{1}{2}m{{v}^{2}}{{\cos }^{2}}\theta \]
c) Total mechanical energy is the maximum?
Ans: Total energy at any point of projectile motion will be the same. Mathematically, at the highest point;
\[{{\left( K.E. \right)}_{H}}+{{\left( P.E. \right)}_{H}}=\frac{1}{2}m{{v}^{2}}{{\cos }^{2}}\theta +\frac{1}{2}m{{u}^{2}}{{\sin }^{2}}\theta \]
\[\Rightarrow {{\left( K.E. \right)}_{H}}+{{\left( P.E. \right)}_{H}}=\frac{1}{2}m{{v}^{2}}\left( {{\cos }^{2}}\theta +{{\sin }^{2}}\theta \right)\]
\[\Rightarrow {{\left( K.E. \right)}_{H}}+{{\left( P.E. \right)}_{H}}=\frac{1}{2}m{{v}^{2}}\]
5. A cyclist starts from the centre \[O\] of a circular park of radius \[1km\], reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 4.21. If the round trip takes \[10\]min, what is the
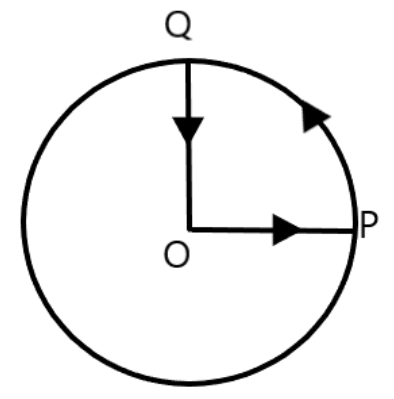
a) Net displacement?
Ans: Displacement is given by the shortest distance between the initial and final positions of a body which is travelling. In the provided case, the cyclist comes to the starting point after cycling for \[10\]minutes. Therefore, his net displacement is zero.
b) Average velocity?
Ans: Average velocity is given by the relation:
\[Average\,velocity=\frac{Net\,displacement}{Total\,time}\]
Because the net displacement of the cyclist is zero, his average velocity will also be zero.
c) Average speed of the cyclist?
Ans: Average speed of the cyclist is given by the formula:
\[Average\,speed=\frac{Total\,path\,length\,}{Total\,time}\]
Total path length is given as \[=OP+PQ+QO\]
\[\Rightarrow 1+\frac{1}{4}\left( 2\pi \times 1 \right)+1\]
\[\Rightarrow 2+\frac{1}{2}\pi =3.570km\]
Time taken can be given as \[10\min =\frac{10}{60}=\frac{1}{6}h\]
Average speed \[=\frac{3.570}{\frac{1}{6}}=21.42km/h\]
6. A passenger arriving in a new town wishes to go from the station to a hotel located \[10\]km away on a straight road from the station. A dishonest cabman takes him along a circuitous path \[23km\]long and reaches the hotel in \[28\min \]. What is
a) The average speed of the taxi?
Ans: Given that,
Total distance travelled can be given as \[=23km\]
Total time taken can be given as \[=28\min =\frac{28}{60}h\]
\[Average\,speed\,of\,the\,taxi=\frac{Total\,distance\,travelled}{Total\,time\,taken}\]
\[\Rightarrow Average\,speed\,of\,the\,taxi=\frac{23}{\left( \frac{28}{60} \right)}=49.29km/h\]
b) The magnitude of average velocity? Are they two equal?
Ans: Given that,
Distance between the hotel and the station \[=10km=\] Displacement of the car.
\[Average\,velocity=\frac{10}{\left( \frac{28}{60} \right)}=21.43km/h\]
Therefore, the two physical quantities (average speed and average velocity) are unequal.
7. Rain is falling vertically with a speed of \[30m/s\]. A woman rides a bicycle with a speed of \[10m/s\]in the north to south direction. What is the direction in which she should hold her umbrella?
Ans: The described situation is depicted in the given figure.
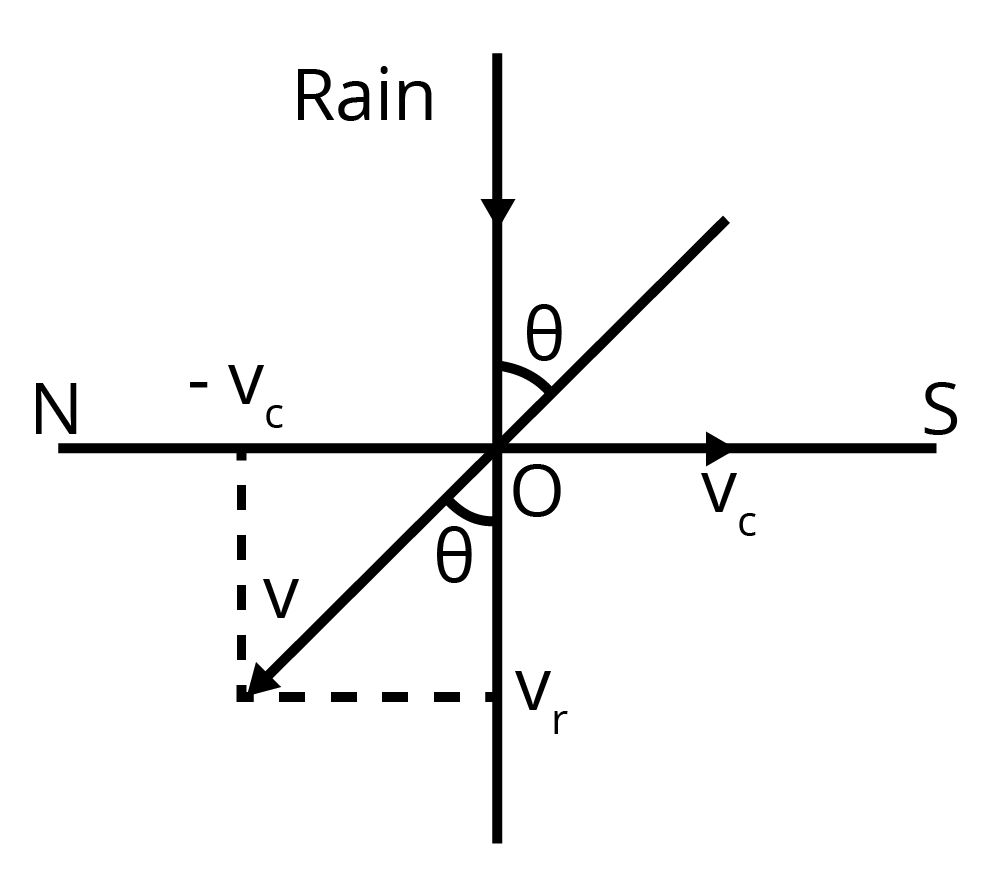
Here,
\[{{v}_{c}}=\] Velocity of the cyclist
\[{{v}_{r}}=\] Velocity of falling rain
To protect herself from the rain, the woman should hold her umbrella in the direction of the relative velocity (v) of the rain with respect to the woman.
\[v={{v}_{t}}+\left( -{{v}_{c}} \right)\Rightarrow v=30+\left( -10 \right)=20m/s\]
Now,
\[\tan \theta =\frac{{{v}_{c}}}{{{v}_{r}}}=\frac{10}{30}\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( 0.333 \right)=18{}^\circ \]
Therefore, the woman must hold the umbrella toward the south, at an angle of nearly \[18{}^\circ \] with the vertical.
8. The ceiling of a long hall is \[25m\] high. What is the maximum horizontal distance that a ball thrown with a speed of \[40m/s\] can go without hitting the ceiling of the hall?
Ans: Given that,
Speed of the ball is given as, \[u=40m/s\]
Maximum height is given as, h = 25 m
In projectile motion, the maximum height attained by a body projected at an angle θ, is given by the formula:
\[h=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\]
\[\Rightarrow 25=\frac{{{40}^{2}}}{2\times 9.8}\]
\[\Rightarrow {{\sin }^{2}}\theta =0.30625\]
\[\Rightarrow \sin \theta =0.5534\]
\[\Rightarrow \theta ={{\sin }^{-1}}\left( 0.5534 \right)=33.60{}^\circ \]
Horizontal Range, \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\]
\[\Rightarrow R=\frac{{{40}^{2}}\times \sin 2\left( 33.60 \right)}{9.8}\]
\[\Rightarrow R=\frac{1600\times \sin 67.2}{9.8}\]
\[\Rightarrow R=\frac{1600\times 0.922}{9.8}=150.53m\]
9. An aircraft is flying at a height of \[3400m\] above the ground. If the angle subtended at a ground observation point by the aircraft positions \[10s\] apart is \[30{}^\circ \], what is the speed of the aircraft?
Ans: The positions of the observer and the aircraft are depicted in the following figure.
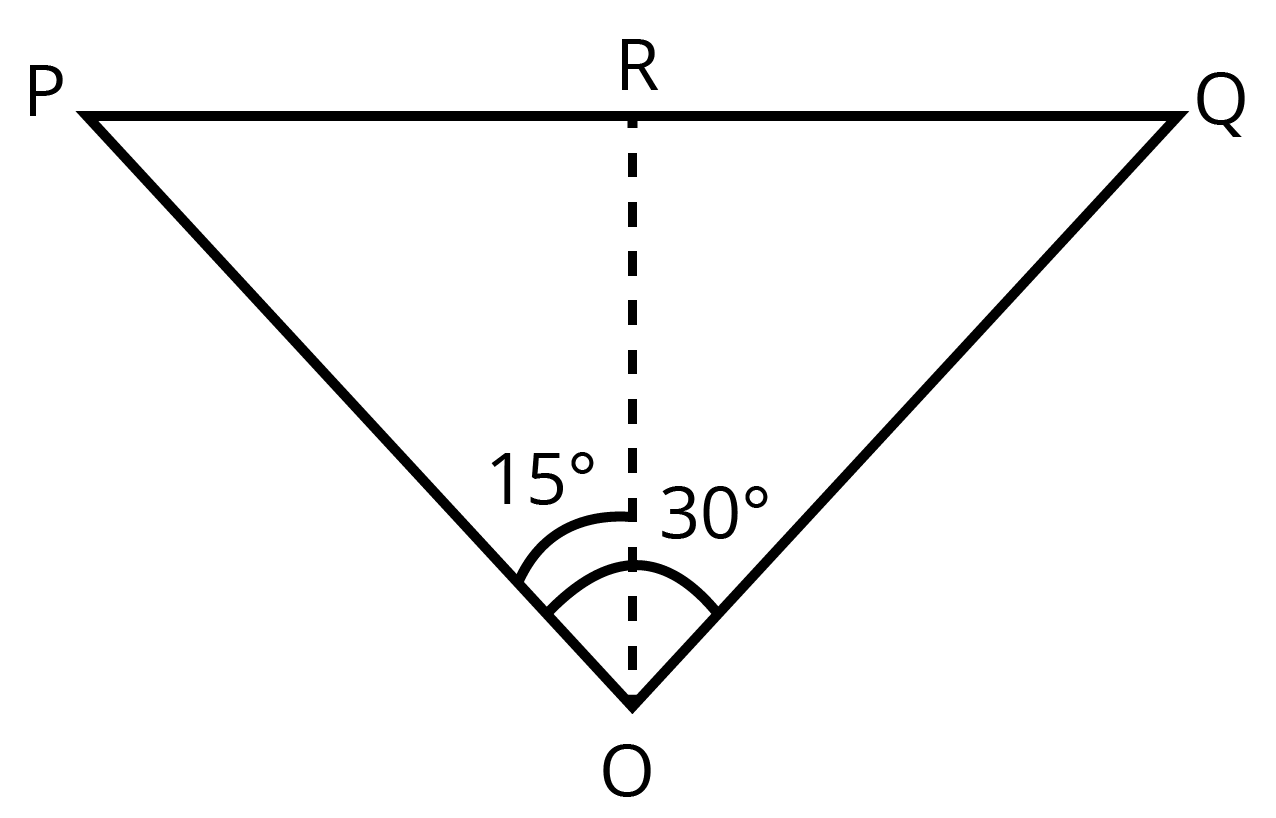
Height of the aircraft from ground is given as, \[OR=3400m\]
Angle subtended between the positions is given as, \[\angle POQ=30{}^\circ \]
Time \[=10s\]
In \[\Delta PRO\] we can write:
\[\tan 15{}^\circ =\frac{PR}{OR}\]
\[\Rightarrow PR=OR\tan 15{}^\circ \]
\[\Rightarrow PR=3400\times \tan 15{}^\circ \]
\[\Delta PRO\]is similar to \[\Delta RQO\].
\[PR=RQ\]
\[\Rightarrow PQ=PR+RQ\]
\[\Rightarrow PQ=2PR=2\times 3400\tan 15{}^\circ \]
\[\Rightarrow PQ=6800\times 0.268=1822.4m\]
Therefore, speed of the aircraft \[=\frac{1822.4}{10}=182.24m/s\]
10. A bullet fired at an angle of \[30{}^\circ \]with the horizontal hits the ground \[3km\] away. By adjusting its angle of projection, can one hope to hit a target \[5km\] away? Assume the muzzle speed to the fixed, and neglect air resistance.
Ans: Range is given as, \[R=3km\]
Angle of projection is given \[=30{}^\circ \]
Acceleration due to gravity, \[g=9.8m/{{s}^{2}}\]
Horizontal range for the projection velocity \[{{u}_{0}}\], is given by the formula:
\[R=\frac{{{u}^{2}}\sin 2\theta }{g}\]
\[\Rightarrow 3=\frac{{{u}_{0}}^{2}}{g}\sin 60{}^\circ \]
\[\Rightarrow \sqrt{3}\times \sqrt{3}=\frac{{{u}_{0}}^{2}}{g}\times \frac{\sqrt{3}}{2}\]…… \[\left[ \because 3=\sqrt{3}\times \sqrt{3} \right]\]
\[\frac{{{u}_{0}}^{2}}{g}=2\sqrt{3}\] …… (1)
The maximum range, \[{{R}_{\max }}\], is achieved by the bullet when it is fired at an angle of \[45{}^\circ \]with the horizontal, that is,
\[{{R}_{\max }}=\frac{{{u}_{0}}^{2}}{g}\] …… (2)
On comparing equations (1) and (2), we get:
\[\Rightarrow {{R}_{\max }}=2\sqrt{3}=2\times 1.732=3.46km\]
Therefore, the bullet will not hit a target \[5km\]away.
4 Marks Questions
1. Given \[a+b+c+d=0\], which of the following statements are correct:
a) \[a\], \[b\], \[c\], and \[d\] must each be a null vector.
Ans: Incorrect.
To make \[a+b+c+d=0\], it is not important to have all the four given vectors to be null vectors. There are many other combinations which can give the addition of vectors as zero.
b) The magnitude of \[a+c\] equals the magnitude of \[\left( b+d \right)\].
Ans: Correct.
\[a+b+c+d=0\]
\[a+c=-\left( b+d \right)\]Taking modulus on both the sides, we obtain:
\[\left| a+c \right|=\left| -\left( b+d \right) \right|=\left| b+d \right|\]
Therefore, the magnitude of \[a+c\] is the same as the magnitude of \[\left( b+d \right)\].
c) The magnitude of \[a\]can never be greater than the sum of the magnitudes of \[b\], \[c\], and \[d\].
Ans: Correct.
\[a+b+c+d=0\]
\[a=b+c+d\]
Taking modulus on both sides, we obtain:
\[\left| a \right|=\left| b+c+d \right|\]
\[\left| a \right|\le \left| b \right|+\left| c \right|+\left| d \right|\] ...... (1)
Equation (1) shows that the magnitude of \[a\]is equal to or less than the sum of the magnitude of \[b\], \[c\], and \[d\].
Therefore, the magnitude of vector \[a\]can never be greater than the sum of the magnitudes of \[b\], \[c\], and \[d\].
d) \[b+c\] must lie in the plane of \[a\] and \[d\]if \[a\]and \[d\]are not collinear, and in the line.
Ans: Correct.
For \[a+b+c+d=0\]
\[a+\left( b+c \right)+d=0\]
The resultant sum of the three vectors \[a\], \[\left( b+c \right)\], and \[d\]is equal to zero only if \[\left( b+c \right)\] lie in a plane containing \[a\]and \[d\], assuming that these three vectors are represented by the three sides of a triangle.
If \[a\]and \[d\] are collinear, then it implies that the vector \[\left( b+c \right)\] is in the line of a and d. This statement holds only when the vector sum of all the vectors will be zero.
2. In a harbour, wind is blowing at the speed of \[72km/h\] and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of \[51km/h\] to the north, what is the direction of the flag on the mast of the boat?
Ans: Velocity of the boat is given as \[{{v}_{b}}=51km/h\]
Velocity of the wind is given as \[{{v}_{w}}=72km/h\]
The flag is fluttering in the north-east direction. It means that the wind is blowing toward the north-east direction. When the ship starts sailing toward the north, the flag will move along the direction of the relative velocity (\[{{v}_{wb}}\]) of the wind with respect to the boat.
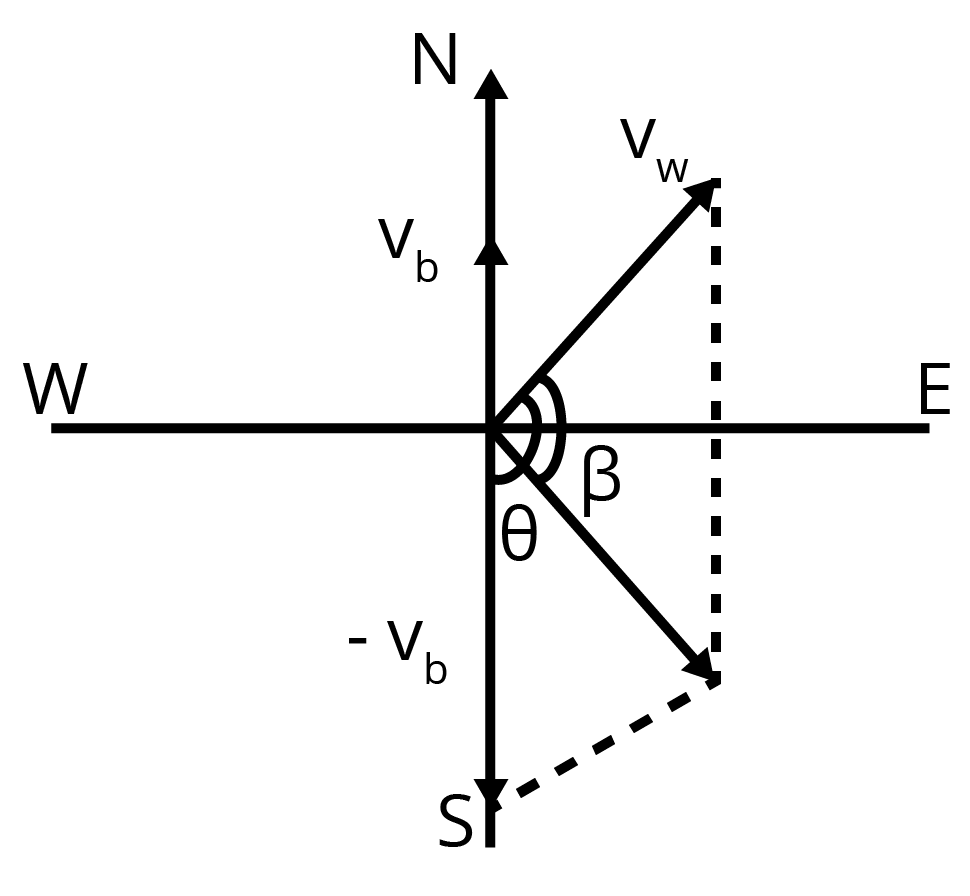
The angle between \[{{v}_{w}}\] and \[\left( -{{v}_{b}} \right)\] \[=90{}^\circ +45{}^\circ \].
\[\tan \beta =\frac{51\sin \left( 90+45 \right)}{72+51\cos \left( 90+45 \right)}\]
\[\Rightarrow \tan \beta =\frac{51\sin \left( 45 \right){}^\circ }{72+51\left( -\cos 45{}^\circ \right)}=\frac{51\times \frac{1}{\sqrt{2}}}{72-51\times \frac{1}{\sqrt{2}}}\]
\[\Rightarrow \tan \beta =\frac{51}{72\sqrt{2}-51}=\frac{51}{72\times 1.414-51}=\frac{51}{50.800}\]
\[\Rightarrow \beta ={{\tan }^{-1}}\left( 1.0038 \right)=45.11{}^\circ \]
Angle with respect to the east direction \[=45.11{}^\circ -45{}^\circ =0.11{}^\circ \].
Therefore, the flag will flutter almost due east.
3. A fighter plane flying horizontally at an altitude of \[1.5km\]with speed \[720km/h\] passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take \[g=10m/{{s}^{2}}\] ).
Ans: Height of the fighter plane is given as \[1.5km=1500m\].
Speed of the fighter plane is given as, v = 720 km/h = 200 m/s
Let \[\theta \] be the angle with the vertical so that the shell hits the plane. The situation is depicted in the given figure.
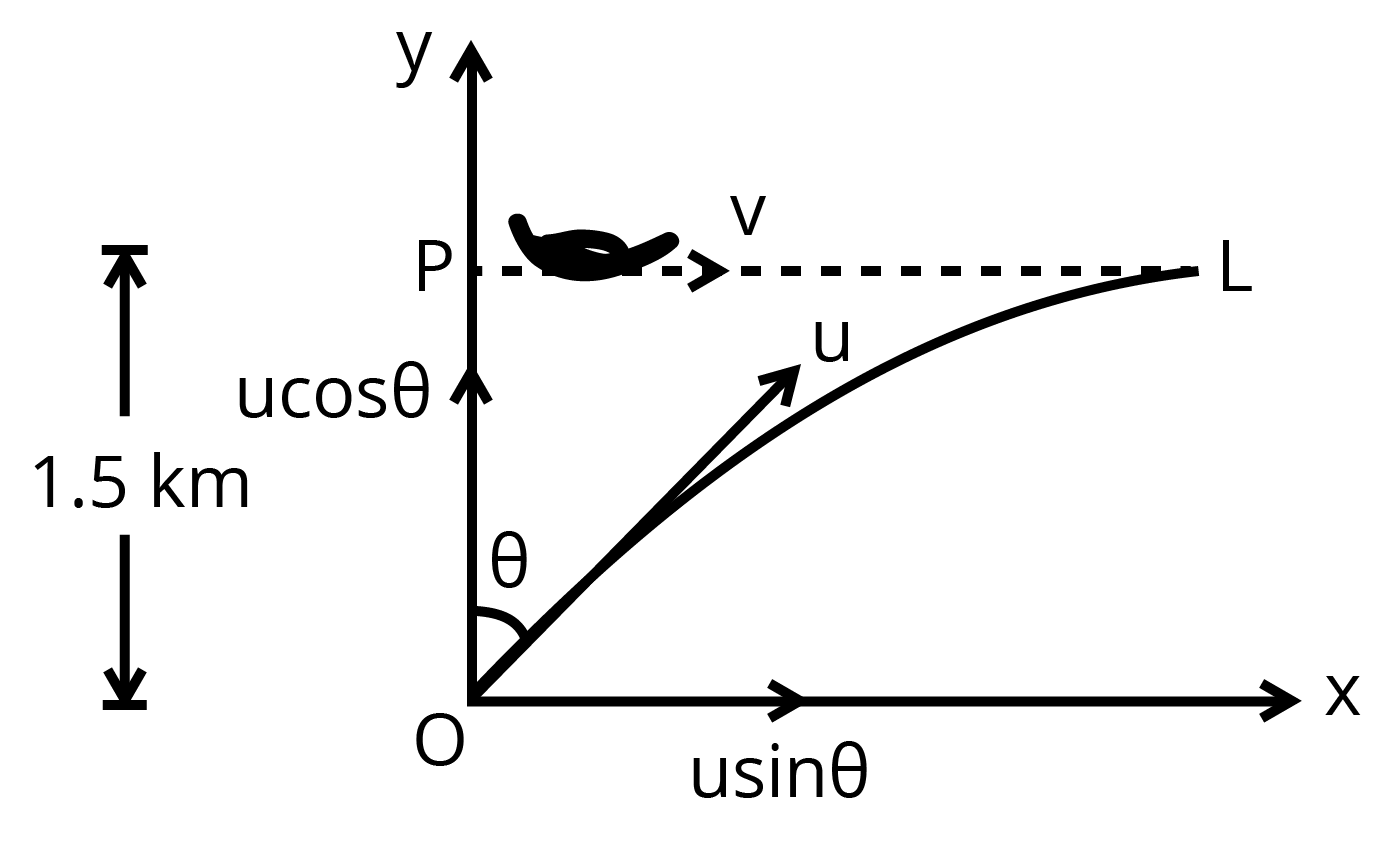
Muzzle velocity of the gun, \[u=600m/s\]
Time taken by the shell to hit the plane \[=t\]
Horizontal distance travelled by the shell \[={{u}_{x}}t\]
Distance travelled by the plane \[=vt\]
The shell hits the plane. Therefore, these two distances should be equal.
\[{{u}_{x}}t=vt\]
\[u\sin \theta =v\]
\[\sin \theta =\frac{v}{u}\]
\[\Rightarrow \sin \theta =\frac{200}{600}=\frac{1}{3}=0.33\]
\[\theta ={{\sin }^{-1}}\left( 0.33 \right)\]
\[\Rightarrow \theta =19.5{}^\circ \]
In order to avoid being hit by the shell, the pilot must fly the plane at an altitude (H) higher than the maximum height achieved by the shell.
\[H=\frac{{{u}^{2}}{{\sin }^{2}}\left( 90-\theta \right)}{2g}\]
\[\Rightarrow H=\frac{{{\left( 600 \right)}^{2}}{{\cos }^{2}}\theta }{2g}\]
\[\Rightarrow H=\frac{360000\times {{\cos }^{2}}19.5}{2\times 10}\]
\[\Rightarrow H=18000\times {{\left( 0.943 \right)}^{2}}\]
\[\Rightarrow H=16006.42m\]
\[\Rightarrow H=16km\], which is the required height.
5 Marks Questions
1.
a) What is the angle between \[\vec{A}\] and \[\vec{B}\]. If \[\vec{A}\] and \[\vec{B}\] denote the adjacent sides of a parallelogram drawn from a point and the area of the parallelogram is \[\frac{1}{2}AB\]?
Ans: Area of a parallelogram can be given as \[=\left| \vec{A}\times \vec{B} \right|\]
Area of parallelogram can be given as \[=AB\sin \theta \] (Applying cross product)
Given data is,
Area of parallelogram \[=\frac{1}{2}AB\]
So, \[\frac{1}{2}=AB=AB\sin \theta \]
\[\Rightarrow \frac{1}{2}=\sin \theta \]
\[\Rightarrow \theta ={{\sin }^{-1}}\left( \frac{1}{2} \right)\]
\[\Rightarrow \theta =30{}^\circ \]
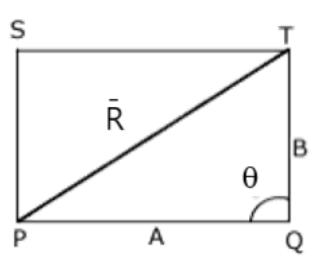
Clearly, area of a parallelogram can be given as \[=\left| \vec{A}\times \vec{B} \right|\]
b) State and prove triangular law of vector addition.
Ans: Triangular law of vector addition states that if two vectors can be expressed both in magnitude and direction by the sides of a triangle taken in order then their resultant is given by the third side of the triangle taken in the opposite order.
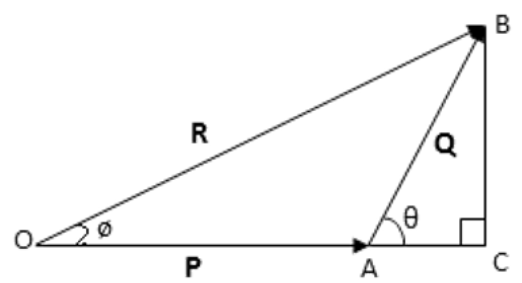
In \[\Delta ADC\],
\[{{\left( AC \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( DC \right)}^{2}}\]
\[\Rightarrow {{\left( AC \right)}^{2}}={{\left( AB+BD \right)}^{2}}+{{\left( DC \right)}^{2}}\]
\[\Rightarrow {{\left( AC \right)}^{2}}=A{{B}^{2}}+B{{D}^{2}}+2\left( AB \right)\left( BD \right)+{{\left( DC \right)}^{2}}\]
\[\Rightarrow {{\left( AC \right)}^{2}}={{P}^{2}}+{{\left( Q\cos \theta \right)}^{2}}+2P\left( Q\cos \theta \right)+{{\left( Q\sin \theta \right)}^{2}}\]
\[\Rightarrow {{\left( AC \right)}^{2}}={{P}^{2}}+{{Q}^{2}}\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta \right)+2PQ\cos \theta \]
\[\left( \because \frac{BD}{BC}=\cos \theta \right)\] and \[\left( \because \frac{CD}{BC}=\sin \theta \right)\]
\[\Rightarrow {{R}^{2}}={{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta \]
\[\left( \because {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \right)\]
\[\Rightarrow R=\sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta }\]
Hence proved.
2. Establish the following vector inequalities geometrically or otherwise:
When does the equality sign above apply?
(a) \[\left| a+b \right|\le \left| a \right|+\left| b \right|\]
Ans: Let two vectors \[\vec{a}\] and \[\vec{b}\] be represented by the adjacent sides of a parallelogram
OMNP, as shown in the given figure.
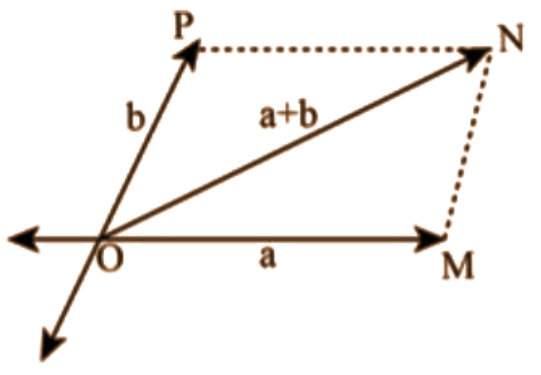
Here, we can express:
\[\left| \overrightarrow{OM} \right|=\left| {\vec{a}} \right|\] …… (1)
\[\left| \overrightarrow{MN} \right|=\left| \overrightarrow{OP} \right|=\left| {\vec{b}} \right|\] …… (2)
\[\left| \overrightarrow{ON} \right|=\left| \vec{\alpha }+\vec{\beta } \right|\] …… (3)
We know that, in a triangle, each side is smaller than the sum of the other two sides.
Therefore, in \[\Delta OMN\], we have:
\[ON<OM+MN\]
\[\left| \vec{a}+\vec{b} \right|<\left| {\vec{a}} \right|+\left| {\vec{b}} \right|\] …… (4)
If the two vectors and act along a straight line in the same direction, then it can be written as:
\[\left| \vec{a}+\vec{b} \right|=\left| {\vec{a}} \right|+\left| {\vec{b}} \right|\] …… (5)
Combining equations (4) and (5), we obtain:
\[\left| \vec{a}+\vec{b} \right|\le \left| {\vec{a}} \right|+\left| {\vec{b}} \right|\]
(b) \[\left| a+b \right|\ge \left| \left| a \right|-\left| b \right| \right|\]
Ans: Let two vectors \[\vec{a}\] and \[\vec{b}\] be represented by the adjacent sides of a parallelogram OMNP, as depicted in the given figure.

Here, we can express:
\[\left| \overrightarrow{OM} \right|=\left| {\vec{a}} \right|\]
\[\left| \overrightarrow{MN} \right|=\left| \overrightarrow{OP} \right|=\left| {\vec{b}} \right|\]
\[\left| \overrightarrow{ON} \right|=\left| \vec{a}+\vec{b} \right|\]
We know that, in a triangle, each side is smaller than the sum of the other two sides.
Therefore, in \[\Delta OMN\], we can write:
\[ON+MN>OM\]
\[ON+OM>MN\]
\[\left| \overrightarrow{ON} \right|>\left| \overrightarrow{OM}-\overrightarrow{OP} \right|\]
\[\left( \because OP=MN \right)\]
\[\left| \vec{a}+\vec{b} \right|>\left| {\vec{a}} \right|-\left| {\vec{b}} \right|\] …... (4)
If the two vectors \[\vec{a}\] and \[\vec{b}\] act along a straight line in the same direction, then we can express:
\[\left| \vec{a}+\vec{b} \right|=\left| {\vec{a}} \right|-\left| {\vec{b}} \right|\] …... (5)
Combining equations (4) and (5), we get:
\[\left| \vec{a}+\vec{b} \right|\le \left| {\vec{a}} \right|-\left| {\vec{b}} \right|\]
(c) \[\left| a-b \right|\le \left| a \right|+\left| b \right|\]
Ans: Let two vectors \[\vec{a}\] and \[\vec{b}\] be represented by the adjacent sides of a parallelogram PORS, as depicted in the given figure.
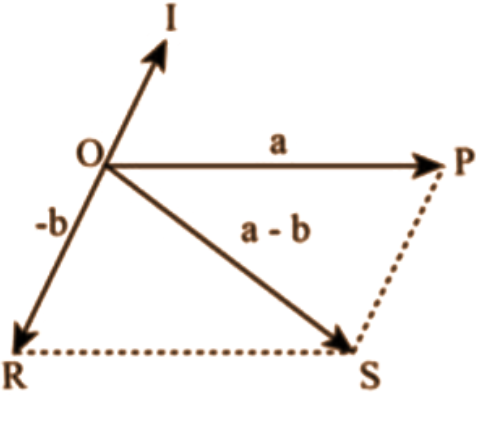
Here we can write:
\[\left| \overrightarrow{OR} \right|=\left| \overrightarrow{PS} \right|=\left| {\vec{b}} \right|\] …… (1)
\[\left| \overrightarrow{OP} \right|=\left| {\vec{a}} \right|\] …… (2)
We know that, in a triangle, each side is smaller than the sum of the other two sides. Therefore, in \[\Delta OSP\] we have:
\[OS<OP+PS\]
\[\left| \vec{a}-\vec{b} \right|<\left| {\vec{a}} \right|+\left| -\vec{b} \right|\]
\[\left| \vec{a}-\vec{b} \right|<\left| {\vec{a}} \right|+\left| {\vec{b}} \right|\] …… (3)
If the two vectors act in a straight line but in opposite directions, then we can express:
\[\left| \vec{a}-\vec{b} \right|=\left| {\vec{a}} \right|+\left| {\vec{b}} \right|\] …… (4)
Combining equations (3) and (4) we get:
\[\left| \vec{a}-\vec{b} \right|\le \left| {\vec{a}} \right|+\left| {\vec{b}} \right|\]
(d) \[\left| a-b \right|\ge \left| \left| a \right|-\left| b \right| \right|\]
Ans: Let two vectors and be represented by the adjacent sides of a parallelogram PORS, as shown in the given figure.

The following relations can be written for the given parallelogram.
\[OS+PS>OP\] …… (1)
\[OS>OP-PS\] …… (2)
\[\left| \vec{a}-\vec{b} \right|>\left| {\vec{a}} \right|-\left| -\vec{b} \right|\] …… (3)
The quantity on the LHS is always positive and that on the RHS can be positive or negative.
To make both quantities positive, we take modulus on both sides as:
\[\left| \vec{a}-\vec{b} \right|>\left| \left| {\vec{a}} \right|-\left| -\vec{b} \right| \right|\]
\[\left| \vec{a}-\vec{b} \right|>\left| {\vec{a}} \right|-\left| {\vec{b}} \right|\] …… (4)
If the two vectors act in a straight line but in the opposite directions, then we can write:
\[\left| \vec{a}-\vec{b} \right|=\left| {\vec{a}} \right|-\left| {\vec{b}} \right|\] …… (5)
Combining equations (4) and (5), we get:
\[\left| \vec{a}-\vec{b} \right|\ge \left| {\vec{a}} \right|-\left| {\vec{b}} \right|\]
3. On an open ground, a motorist follows a track that turns to his left by an angle of \[60{}^\circ \] after every \[500m\]. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
Ans: The path persuaded by the motorist is a regular hexagon with side \[500m\], as shown in the following figure.
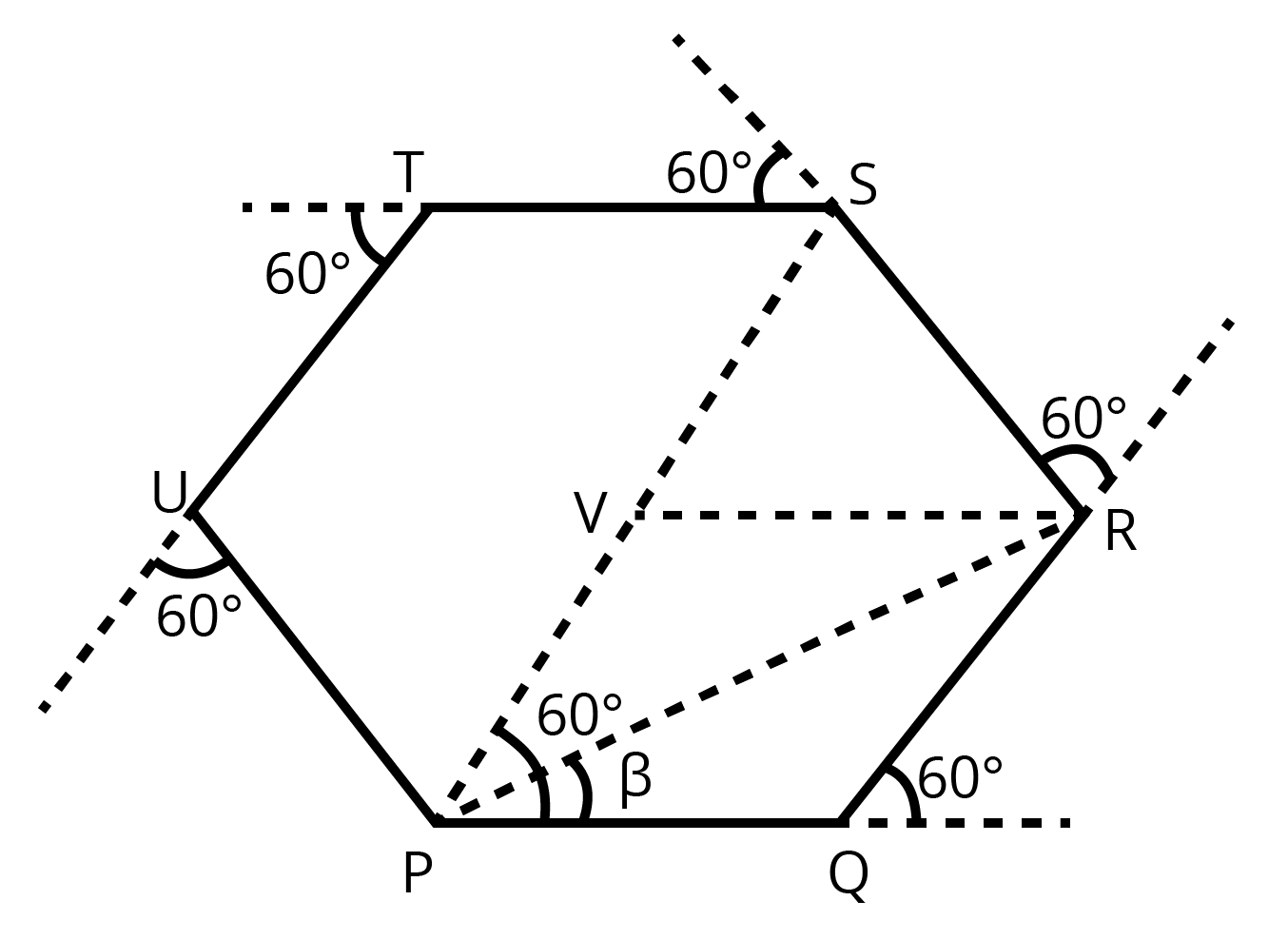
Let the motorist start from the point \[P\].
The motorist takes the third turn at \[S\].
$\therefore$ Magnitude of displacement \[=PS=PV+VS=500+500=1000m\]
Total path length \[=PQ+QR+RS=500+500+500=1500m\]
The motorist takes the sixth turn at point \[P\], which is the starting point.
$\therefore$ Magnitude of displacement can be given \[=0\]
Total path length \[=PQ+QR+RS+ST+TU+UP\]
\[\Rightarrow 500+500+500+500+500+500=3000m\]
The motorist takes the eight turns at point \[R\]
$\therefore$ Magnitude of displacement can be given\[=PR\]
\[\Rightarrow PR=\sqrt{P{{Q}^{2}}+Q{{R}^{2}}+2\left( PQ \right)\cdot \left( QR \right)\cos 60{}^\circ }\]
\[\Rightarrow PR=\sqrt{{{500}^{2}}+{{500}^{2}}+\left( 2\times 500\times 500\times \cos 60{}^\circ \right)}\]
\[\Rightarrow PR=\sqrt{250000+250000+500000\times \frac{1}{2}}\]
\[\Rightarrow PR=866.03m\]
\[\beta ={{\tan }^{-1}}\left( \frac{500\sin 60{}^\circ }{500+500\cos 60{}^\circ } \right)\]
Therefore, the magnitude of displacement is \[866.03m\] at an angle of \[30{}^\circ \] with PR.
Total path length \[=Circumference\,of\,the\,hexagon+PQ+QR\]
\[\Rightarrow 6\times 500+500+500=4000m\]
The magnitude of displacement and the total path length corresponding to the required turns is depicted in the following table:
Turn | Magnitude of Displacement(M) | Total Path Length(m) |
Third | 1000 | 1500 |
Sixth | 0 | 3000 |
Eighth | 866.03, \[30{}^\circ \] | 4000 |
4. A particle starts from the origin at \[t=0s\]with a velocity of \[10\hat{j}m/s\] and moves in the x-y plane with a constant acceleration of \[\left( 8\hat{i}+2\hat{j} \right)m/{{s}^{2}}\].
a) At what time is the x-coordinate of the particle \[16m\]? What is the y-coordinate of the particle at that time?
Ans: Velocity of the particle is given as \[\vec{v}=10.0\hat{j}m/s\]
Acceleration of the particle is given as \[\vec{a}=\frac{d\vec{v}}{dt}=8\hat{i}+2\hat{j}\]
Also,
\[\vec{a}=8\hat{i}+2\hat{j}\]
But,
\[\vec{a}=\frac{d\vec{v}}{dt}=8\hat{i}+2\hat{j}\]
\[d\vec{v}=\left( 8\hat{i}+2\hat{j} \right)dt\]
Integrating both sides:
\[\vec{v}\left( t \right)=8t\hat{i}+2t\hat{j}+\vec{u}\]
Where,
\[\vec{u}=\]Velocity vector of the particle at t = 0
\[\vec{v}=\]Velocity vector of the particle at time t
However,
\[\vec{v}=\frac{dr}{dt}\]
\[d\vec{r}=\vec{v}dt=\left( 8t\hat{i}+2t\hat{j}+\vec{u} \right)dt\]
Integrating the equations with the conditions: at \[t=0\]; \[r=0\]and at \[t=t\]; \[r=r\]
\[\vec{r}=\vec{u}t+\frac{1}{2}\times 8{{t}^{2}}\hat{i}+\frac{1}{2}\times 2{{t}^{2}}\hat{j}\]
\[\Rightarrow \vec{r}=\vec{u}t+4{{t}^{2}}\hat{i}+{{t}^{2}}\hat{j}\]
\[\Rightarrow \vec{r}=\left( 10\hat{j} \right)t+4{{t}^{2}}\hat{i}+{{t}^{2}}\hat{j}\]
\[\Rightarrow x\hat{i}+y\hat{j}=4{{t}^{2}}\hat{i}+\left( 10t+{{t}^{2}} \right)\hat{j}\]
Since the motion of the particle is confined to the x-y plane, on equating the coefficients of \[\hat{i}\] and \[\hat{j}\], we get:
\[x=4{{t}^{2}}\]
\[t={{\left( \frac{x}{4} \right)}^{\frac{1}{2}}}\]
And \[y=10t+{{t}^{2}}\]
When \[x=16m\]:
\[t={{\left( \frac{16}{4} \right)}^{\frac{1}{2}}}=2s\], which is the required time.
\[y=10\times 2+{{2}^{2}}=24m\], which is the required y coordinate.
b) What is the speed of the particle at the time?
Ans: Velocity of the particle can be given by:
\[\vec{v}\left( t \right)=8t\hat{i}+2t\hat{j}+\vec{u}\]
At \[t=2s\]
\[\vec{v}\left( t \right)=8\times 2\hat{i}+2\times 2\hat{j}+10\hat{j}\]
\[\vec{v}\left( t \right)=16\hat{i}+14\hat{j}\]
\[\vec{v}=\sqrt{{{16}^{2}}+{{14}^{2}}}\]
\[\Rightarrow \vec{v}=\sqrt{256+196}=\sqrt{452}\]
\[\Rightarrow \vec{v}=21.26m/s\], which is the required speed.
5. \[\hat{i}\] and \[\hat{j}\] are unit vectors along x- and y-axis respectively. What is the magnitude and direction of the vectors \[\hat{i}+\hat{j}\], and \[\hat{i}-\hat{j}\]? What are the components of a vector along the directions of \[\hat{i}+\hat{j}\] and \[\hat{i}-\hat{j}\]? [You may use graphical method]
Ans: Let us consider a vector \[\vec{P}\], given as:
\[\vec{P}=\hat{i}+\hat{j}\]
\[{{P}_{x}}\hat{i}+{{P}_{y}}\hat{j}=\hat{i}+\hat{j}\]
On comparing the components on both sides, we obtain:
\[{{P}_{x}}={{P}_{y}}=1\]
\[\left| {\vec{P}} \right|=\sqrt{{{P}_{x}}^{2}+{{P}_{y}}^{2}}=\sqrt{{{1}^{2}}+{{1}^{2}}}=\sqrt{2}\]
Therefore, the magnitude of the vector is\[\sqrt{2}\].
Let \[\theta \] be the angle made by the vector \[\vec{P}\], with the x-axis, as shown in the given figure.
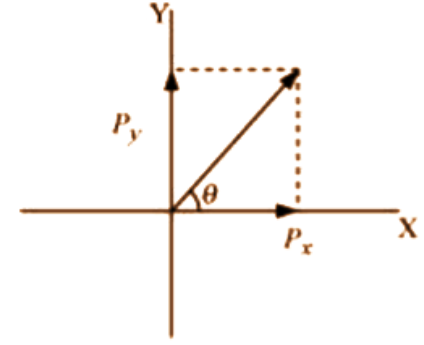
\[\tan \theta =\left( \frac{{{P}_{y}}}{{{P}_{x}}} \right)\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \frac{1}{1} \right)=45{}^\circ \]
Therefore, the vector \[\hat{i}+\hat{j}\] makes an angle of \[45{}^\circ \]with the x-axis.
Let \[\vec{Q}=\hat{i}-\hat{j}\]
\[{{Q}_{x}}\hat{i}-{{Q}_{y}}\hat{j}=\hat{i}-\hat{j}\]
\[{{Q}_{x}}={{Q}_{y}}=1\]
\[\left| {\vec{Q}} \right|=\sqrt{{{Q}_{x}}^{2}+{{Q}_{y}}^{2}}=\sqrt{{{1}^{2}}+{{1}^{2}}}=\sqrt{2}\]
Therefore, the magnitude of the vector \[\hat{i}-\hat{j}\] is \[\sqrt{2}\].
Let \[\theta \] be the angle made by the vector \[\hat{i}-\hat{j}\], with the x- axis, as shown in the following figure.
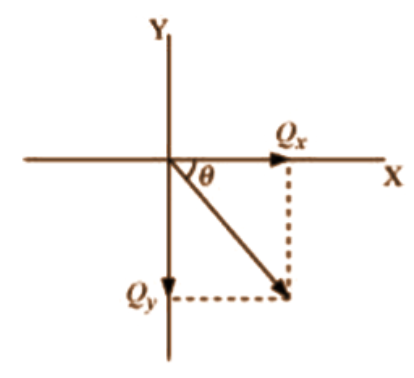
\[\tan \theta =\left( \frac{{{Q}_{y}}}{{{Q}_{x}}} \right)\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \frac{1}{1} \right)=45{}^\circ \]
Therefore, the vector makes an angle of \[45{}^\circ \].
It is given that:
\[\vec{A}=2\hat{i}+3\hat{j}\]
\[{{A}_{x}}\hat{i}+{{A}_{y}}\hat{j}=2\hat{i}+3\hat{j}\]
On comparing the coefficients of \[\hat{i}\] and \[\hat{j}\], we have:
\[{{A}_{x}}=2\]
\[{{A}_{y}}=3\]
\[\left| {\vec{A}} \right|=\sqrt{{{Q}_{x}}^{2}+{{Q}_{y}}^{2}}=\sqrt{{{2}^{2}}+{{3}^{2}}}=\sqrt{13}\]
Let \[\overrightarrow{{{A}_{x}}}\] make an angle with the x-axis as depicted in the given figure.
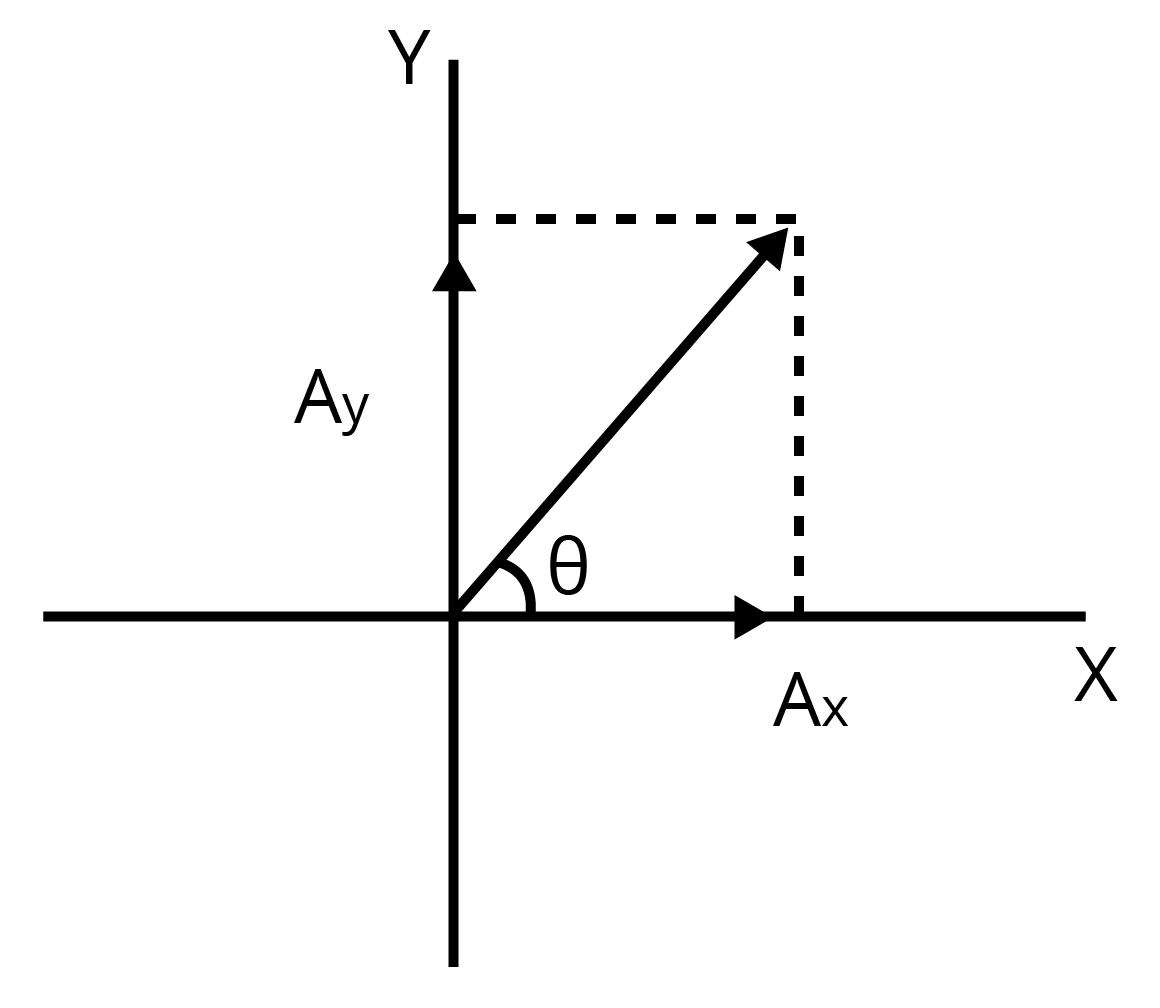
\[\tan \theta =\left( \frac{{{A}_{y}}}{{{A}_{x}}} \right)\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \frac{3}{2} \right)=56.31{}^\circ \]
Angle between the vectors \[2\hat{i}+3\hat{j}\] and \[\hat{i}+\hat{j}\]
\[\theta =56.31{}^\circ -45{}^\circ =11.31{}^\circ \]
Component of vector \[\vec{A}\], along the direction of \[\vec{P}\], making an angle \[\theta \]:
\[=\left( A\cos \theta \right)P=\left( A\cos 11.31{}^\circ \right)\frac{\left( i+j \right)}{\sqrt{2}}\]
\[=\sqrt{13}\times \frac{0.9806}{\sqrt{2}}\left( \hat{i}+\hat{j} \right)=2.5\left( \hat{i}+\hat{j} \right)=\frac{25}{10}\times \sqrt{2}=\frac{5}{\sqrt{2}}\]
Now, let \[\theta \] be the angle between the vectors \[2\hat{i}+3\hat{j}\] and \[\hat{i}+\hat{j}\].
\[\theta =45{}^\circ +56.31{}^\circ =101.31{}^\circ \]
Component of vector \[\vec{A}\], along the direction of \[\vec{Q}\], making an angle \[\theta \]
\[=\left( A\cos \theta \right)\vec{Q}=\left( A\cos \theta \right)\frac{\left( \hat{i}-\hat{j} \right)}{\sqrt{2}}\]
\[=\sqrt{13}\times \cos \left( 901.31{}^\circ \right)\frac{\left( \hat{i}-\hat{j} \right)}{\sqrt{2}}\]
\[=-\sqrt{\frac{13}{2}}\sin 11.30{}^\circ \left( \hat{i}-\hat{j} \right)\]
\[=-2.550\times 0.1961\left( \hat{i}-\hat{j} \right)\]
\[=-0.5\left( \hat{i}-\hat{j} \right)\]\[=-\frac{5}{10}\times \sqrt{2}\]\[=-\frac{1}{\sqrt{2}}\]
6. A cyclist is riding with a speed of \[27km/h\]. As he approaches a circular turn on the road of radius \[80m\], he applies brakes and reduces his speed at the constant rate of \[0.5m/s\] every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Ans: Speed of the cyclist is given as, \[v=27km/h=7.5m/s\]
Radius of the circular turn, \[r=80m\]
Centripetal acceleration can be given as:
\[{{a}_{c}}=\frac{{{v}^{2}}}{r}\]
\[\Rightarrow {{a}_{c}}=\frac{{{\left( 7.5 \right)}^{2}}}{80}=0.7m/s\]
The situation is depicted in the provided figure:
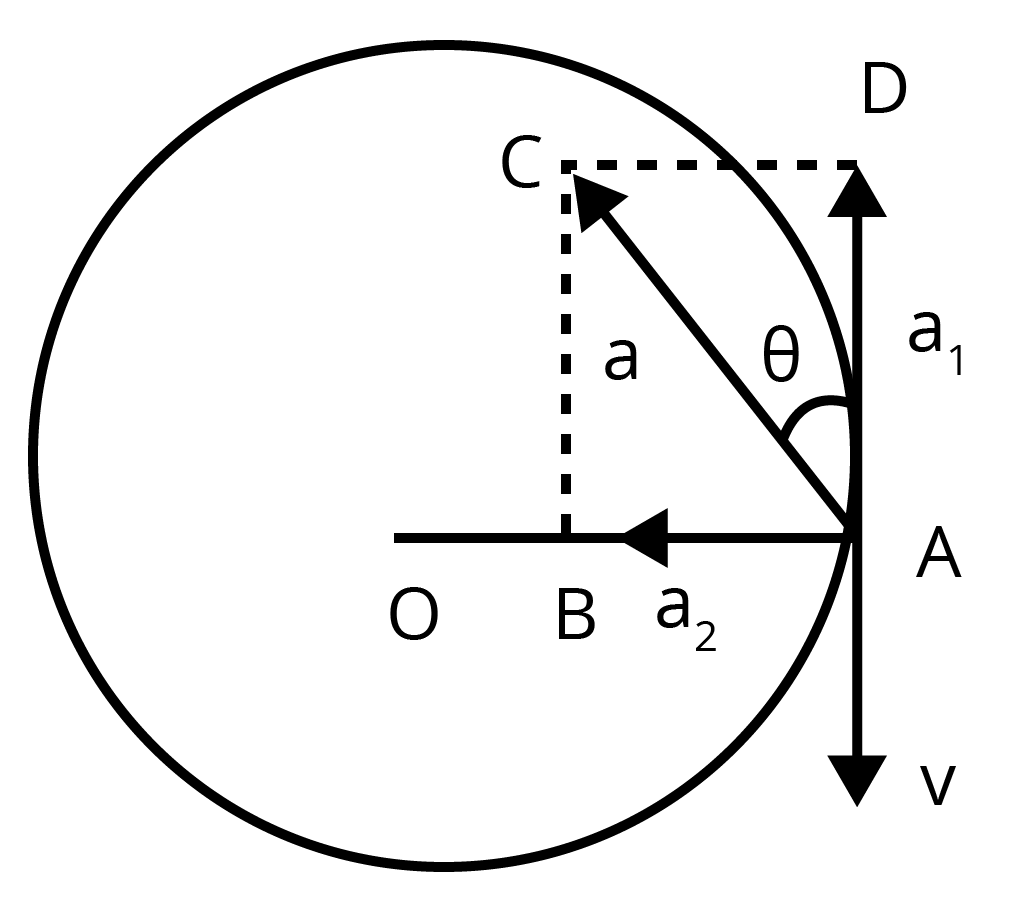
Let us suppose the cyclist begins cycling from point P and moves toward point Q. At point Q, he applies the brakes and decelerates the speed of the bicycle by \[0.5m/{{s}^{2}}\].
This acceleration is along the tangent at Q and in opposite direction to the direction of motion of the cyclist.
Because the angle between \[{{a}_{c}}\] and \[{{a}_{t}}\] is \[{{90}^{\circ }}\] , the resultant acceleration \[a\]is given by:
\[a=\sqrt{{{a}_{c}}^{2}+{{a}_{t}}^{2}}\]
\[\Rightarrow a=\sqrt{{{0.7}^{2}}+{{0.5}^{2}}}\]
\[\Rightarrow a=\sqrt{0.74}=0.86m/{{s}^{2}}\]
\[\tan \theta =\frac{{{a}_{c}}}{{{a}_{t}}}\]
Where \[\theta \] is the angle of the resultant with the direction of velocity.
\[\tan \theta =\frac{0.7}{0.5}=1.4\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( 1.4 \right)\]
\[\Rightarrow \theta =54.46{}^\circ \], which is the required angle of direction here.
7.
a) Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by \[\theta \left( t \right)={{\tan }^{-1}}\left( \frac{{{v}_{0y}}-gt}{{{v}_{0x}}} \right)\]
Ans: Let \[{{v}_{0x}}\]and \[{{v}_{0y}}\]respectively be the initial components of the velocity of the projectile along horizontal (x) and vertical (y) directions.
Let and respectively be the horizontal and vertical components of velocity at a point P.
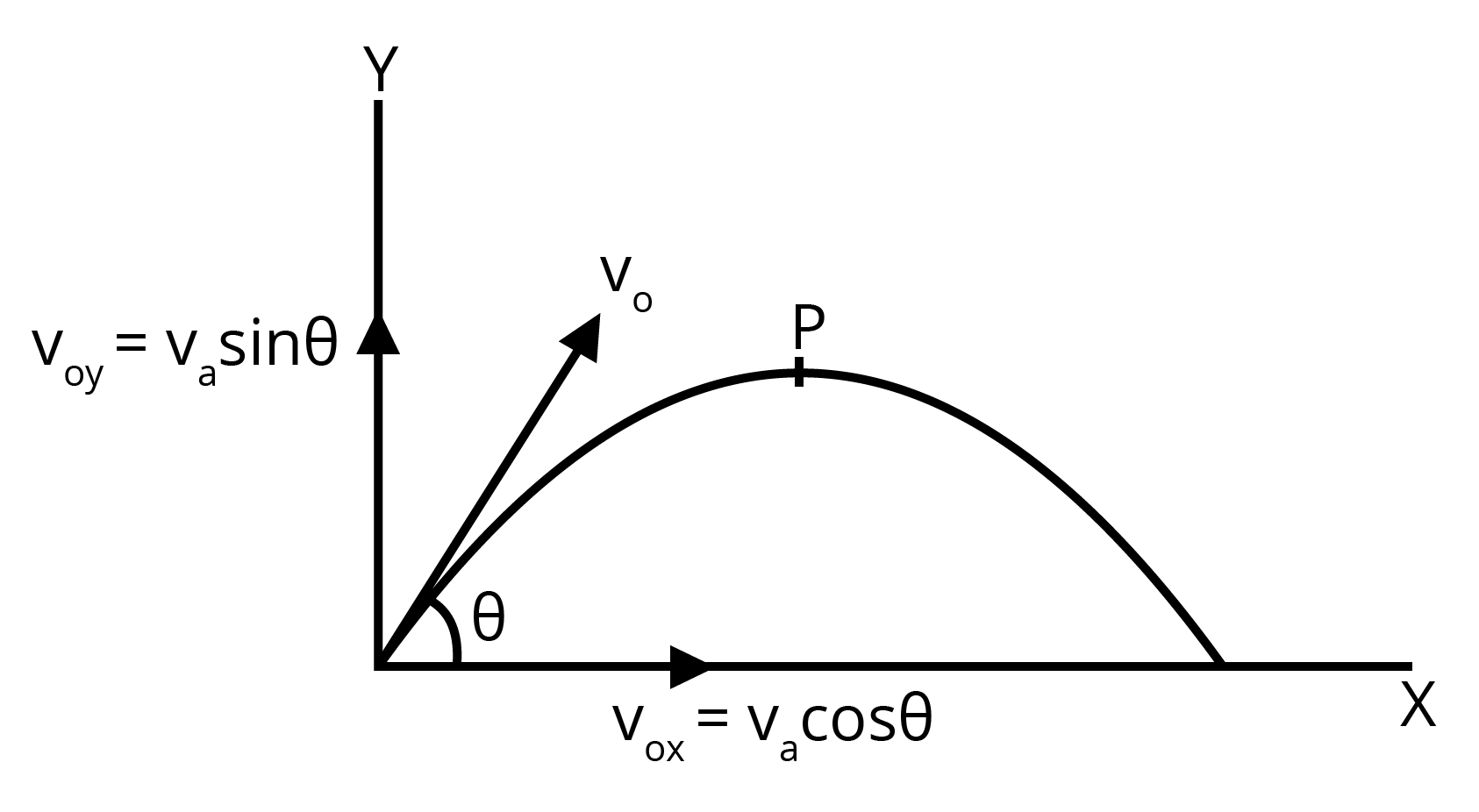
Time taken by the projectile to reach point \[P=t\]
Applying the first equation of motion along the vertical
\[{{v}_{y}}={{v}_{0y}}-gt\]
And, \[{{v}_{x}}={{v}_{0x}}\]
\[\tan \theta =\frac{{{v}_{y}}}{{{v}_{x}}}=\frac{{{v}_{0y}}-gt}{{{v}_{0x}}}\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \frac{{{v}_{0y}}-gt}{{{v}_{0x}}} \right)\]
Hence proved.
b) Show that the projection angle for a projectile launched from the origin is given by \[\theta \left( t \right)={{\tan }^{-1}}\left( \frac{4{{h}_{m}}}{R} \right)\], where the symbols have their usual meaning.
Ans: Maximum vertical height can be given as, \[{{h}_{m}}=\frac{{{u}_{0}}^{2}{{\sin }^{2}}\theta }{2g}\] …… (1)
Horizontal range can be given as, \[R=\frac{{{u}_{0}}^{2}\sin 2\theta }{g}\] …… (2)
Solving equations (1) and (2), we obtain:
\[\frac{{{h}_{m}}}{R}=\frac{{{\sin }^{2}}\theta }{\sin 2\theta }\]
\[\Rightarrow \frac{{{h}_{m}}}{R}=\frac{\sin \theta \times \sin \theta }{2\times 2\sin \theta \cos \theta }\]
\[\Rightarrow \frac{{{h}_{m}}}{R}=\frac{1}{4}\times \frac{\sin \theta }{\cos \theta }=\frac{1}{4}\tan \theta \]
Now,
\[\tan \theta =\frac{4{{h}_{m}}}{R}\]
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \frac{4{{h}_{m}}}{R} \right)\]
Hence proved.
NCERT Solution for Chapter 3 (Motion in a Plane) - How Will It Help a Physics Student?
NCERT Solutions for Motion in a Plane helps students who are preparing for the Class 11 Physics exam. Let us know how exactly will these NCERT Solutions will help a student and what they can find here:
NCERT Solutions Class 11 Physics Chapter 3 is the right thing that can help students to secure good marks in Class 11 exams.
In the NCERT Class 11 Physics Chapter 3 Solutions, students can find the solutions to the questions that have the most chance of coming in the exam.
The motion in a plane Class 11 NCERT Solutions are prepared by some of the best teachers who have expertise in this field; thus, students can be confident in the Class 11 Physics Chapter 3 solutions that they are accurate.
These solutions can be a great help for students who are new in this field.
NCERT Solutions for Chapter 3 (Motion of Plane) [Free] PDF to Download - Other Special Features of the Notes
Studying NCERT solutions for Motion of Plane should be done by the Class 11 students conveniently. Downloading these solutions in PDF will give them access to NCERT Solutions whenever and wherever they want. Students can download the PDF without any cost and retain it till the exam time and study the notes conveniently.
What else does a student get while studying these NCERT Solutions of Motion in a Plane?
Class 11 Physics Chapter 3 NCERT Solutions are the best option available for students to gain basic knowledge in science and learn the concepts of motion in a plane. This will help them in the CBSE Class 11 exam.
Motion in a Plane Class 11 NCERT Solutions PDF is what students require for improving their knowledge in this chapter. They get all the solutions of this chapter in one PDF.
All the concepts and fundamentals are clearly explained in this Motion in a Plane Class 11 solved problems PDF.
NCERT Solutions of Chapter 3 (Motion in a Plane) [CBSE Class 11 Physics] - Important Coverage of the Chapter
Class 11th Physics Chapter 3 NCERT Solutions will cover these vital topics:
Introduction
In the first section, students will be introduced to some concepts that are related to motion in a plane, such as concepts of position, velocity, displacement and acceleration. Explanations relating to these concepts are included in the ch 3 Physics Class 11 NCERT Solutions.
Scalars and Vectors
In the second section, students will gain basic knowledge of scalars and vectors. Topics that are included in this section are the difference between scalars and vectors, directions associated with scalars and vectors, definitions, displacement vectors, triangle law of addition, parallelogram law of addition, the magnitude of displacement and some other topics. Solutions to all these topics can be found in Motion in a Plane Class 11 NCERT Solutions.
Multiplication of Vectors by Real Numbers
In this section, students will learn how to derive an equation by using magnitudes and different formulas. They will also learn to multiply the vectors by using the real numbers.
Addition and Subtraction of Vectors - Graphical Method
In this section, students will learn about the triangle law, parallelogram law of addition and their definitions. They will gain knowledge of formulas of the head-to-tail method, triangle method of vector addition, commutative laws, null vectors and subtraction of vectors in this section.
Resolution of Vectors
With the help of this section, students will learn about the resolution of vectors and its implementation in a straight line. Getting an equation by using real numbers will be easy after learning the concepts of this section.
Vector Addition - Analytical Method
Through this section, a student can learn to add vector numbers by an analytical method along with a graphical method.
Motion in a Plane
In this section, a student will learn about velocity, acceleration, finding out averages, and then finally finding out the motion in a plane.
Motion in a Plane with Constant Acceleration
Here, students will learn how motion in a plane can be treated as two different simultaneous one-dimensional motions, both of which have a constant acceleration in two different perpendicular directions.
Relative Velocity in Three Dimension
In this section, a student will learn to find out three-dimensional motion in a plane by using relative velocity.
Projectile Motion
This section helps in gaining knowledge of the concepts of projectile motion.
Uniform Circular Motion
This section gives a basic knowledge of uniform circular motion.
NCERT Solutions of Chapter 3 - How to Use It and What are the Benefits Rendered?
Vedantu’s CBSE NCERT Solutions Class 11 Physics Chapter 3 is the key to securing good marks in the Class 11 exams. So, how will you use these NCERT Solutions of Chapter 3 in your study plan?
NCERT Solutions are always to be referred for any CBSE subject. These solutions strictly include all the questions following the answer writing guidelines prescribed by the CBSE. Also, generally questions are asked from NCERT books. Thus, students can study these solutions for completing the chapter in an effective and efficient way.
The NCERT Solutions of Chapter 3 can also be referred to while you solve questions and answers. In order to level up your practice, one can easily use these solutions.
NCERT Solutions can be used to brush up on the lessons learned. If you want to revise Chapter 3, you can do it by referring to these NCERT Solutions for Chapter 3.
Now, let us talk about the benefits rendered from studying the NCERT Solutions Chapter 3:
Motion in a Plane Class 11 NCERT Solutions is prepared by some of the best teachers who are experts in this section.
Class 11 Physics Chapter 3 NCERT Solutions are given with practical problems for better understanding.
NCERT Solutions for Class 11 Physics Chapter 3 covers the syllabus.
Conclusion
Students must refer to NCERT solutions so that they can excel in their Class 11 CBSE Exams. These comprehensive notes consist of many important topics which will be beneficial for the students. Students can also download other study material in PDF format at no cost from our website.
Related Study Materials for Class 11 Physics Chapter 3
S.No | Important Other Links for Class 11 Physics Chapter 3 |
1. | |
2. |
CBSE Class 11 Physics Chapter-wise Important Questions
CBSE Class 11 Physics Chapter-wise Important Questions and Answers cover topics from other chapters, helping students prepare thoroughly by focusing on key topics for easier revision.
S.No | Chapter-wise Important Questions for Class 11 Physics |
1 | |
2 | |
3 | |
4 | |
5 | Chapter 6 - Systems of Particles and Rotational Motion Questions |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 |
Additional Study Materials for Class 11 Physics
S.No | Study Materials for Class 11 Physics |
1 | |
2 | |
3 | |
4 |
FAQs on CBSE Important Questions for Class 11 Physics Motion in a Plane - 2025-26
1. What are some of the most important 1-mark questions from Chapter 3, Motion in a Plane?
For the Class 11 Physics exam, several 1-mark questions are frequently asked from this chapter. Key areas to focus on include:
- The condition for the dot product or cross product of two vectors to be zero.
- Defining the trajectory of a projectile.
- The angle of projection for achieving maximum horizontal range (45°).
- Identifying scalar and vector quantities from a given list.
- The direction of centripetal acceleration in uniform circular motion.
2. Which derivations in Motion in a Plane are most important for the CBSE Class 11 exam?
Students should prioritise the following derivations for scoring well in the exam for the session 2025-26:
- Derivation of the expression for the trajectory of a projectile, proving it is a parabola (y = (tanθ)x - (g/2u²cos²θ)x²).
- Derivation of formulas for time of flight (T), maximum height (H), and horizontal range (R) of a projectile.
- Derivation of the expression for centripetal acceleration (a = v²/r) for an object in uniform circular motion.
- The derivation for the resultant of two vectors using the Parallelogram Law of Vector Addition.
3. What is the difference between scalar and vector quantities, and why is this distinction important in this chapter?
A scalar quantity has only magnitude and no direction (e.g., mass, speed, distance, work). A vector quantity has both magnitude and direction (e.g., velocity, acceleration, displacement, force). This distinction is crucial in 'Motion in a Plane' because:
- Motion in a plane is inherently two-dimensional, requiring vectors to describe position, velocity, and acceleration.
- Operations like addition and multiplication are different. Vectors are added using specific laws (Triangle Law, Parallelogram Law), while scalars are added with simple arithmetic.
- Concepts like projectile motion can only be understood by resolving initial velocity into its horizontal and vertical vector components.
4. State and explain the Triangle Law of Vector Addition.
The Triangle Law of Vector Addition states that if two vectors acting on a particle at the same time are represented in magnitude and direction by the two sides of a triangle taken in one order, their resultant vector is represented in magnitude and direction by the third side of the triangle taken in the opposite order. This is a fundamental method used to determine the net effect of two vector quantities.
5. What are the essential formulas for projectile motion that must be remembered for solving numericals?
To solve numerical problems on projectile motion effectively, you must memorise these key formulas:
- Equation of Trajectory: y = (tanθ)x - (g / 2u²cos²θ)x²
- Time of Flight (T): T = 2u sinθ / g
- Maximum Height (H): H = u²sin²θ / 2g
- Horizontal Range (R): R = u²sin(2θ) / g
- Maximum Horizontal Range (R_max): R_max = u² / g (when θ = 45°)
6. What types of numerical problems are important from this chapter for the CBSE 2025-26 exam?
For the upcoming exams, students should practice numericals based on:
- Projectile Motion: Calculating range, height, time of flight, or finding initial velocity/angle of projection given other parameters. A common question involves a cricketer throwing a ball or a bullet fired from a gun.
- Circular Motion: Calculating centripetal acceleration or force for objects like a stone whirled in a circle or a car on a circular track.
- Relative Velocity: Problems involving river-boat scenarios (crossing a river) and rain-person scenarios (the angle to hold an umbrella).
- Vector Operations: Finding the resultant of vectors, unit vectors, and problems involving dot and cross products.
7. A body in uniform circular motion has constant speed, yet it is said to be accelerating. How is this possible?
This is a classic conceptual question. Acceleration is the rate of change of velocity, not speed. Velocity is a vector quantity, having both magnitude (speed) and direction. In uniform circular motion:
- The speed of the body remains constant.
- The direction of motion changes continuously at every point along the circular path.
- Since the direction of velocity is changing, the velocity itself is changing, which means there must be an acceleration.
- This acceleration, called centripetal acceleration, is always directed towards the centre of the circle, perpendicular to the velocity vector at any point.
8. How can two different angles of projection result in the same horizontal range?
A projectile can have the same horizontal range (R) for two different angles of projection that are complementary to each other. If one angle is θ, the other is (90° - θ). This happens because the formula for range, R = u²sin(2θ)/g, gives the same value for both angles:
- For angle θ, the range is R₁ = u²sin(2θ)/g.
- For angle (90° - θ), the range is R₂ = u²sin[2(90° - θ)]/g = u²sin(180° - 2θ)/g.
- Since sin(180° - x) = sin(x), we get R₂ = u²sin(2θ)/g.
Thus, R₁ = R₂. For example, the range is the same for projection angles of 30° and 60°.
9. How should one approach solving problems involving relative velocity in river-boat scenarios to avoid common mistakes?
To solve river-boat problems accurately, follow this strategic approach:
- Identify all vectors: Clearly define the velocity of the boat in still water (v_b), the velocity of the river current (v_r), and the resultant velocity of the boat with respect to the ground (v).
- Use a coordinate system: Align the y-axis with the direction of crossing the river (width) and the x-axis with the direction of the river flow.
- Resolve vectors: The velocity of the boat (v_b) should be resolved into components if it is directed at an angle to the bank. The river velocity (v_r) will only have an x-component.
- Separate motions: The time to cross the river depends only on the y-component of the resultant velocity. The drift (downstream distance) depends only on the x-component of the resultant velocity and the time taken to cross.
- Common Mistake: A frequent error is using the boat's speed (v_b) directly to calculate the time to cross when it's moving at an angle. Always use the component of velocity perpendicular to the river flow for calculating time.
10. What is the physical significance of the dot product and cross product of two vectors?
The dot and cross products have significant physical interpretations that are important for exams:
- Dot Product (Scalar Product): Represents the projection of one vector onto another. It results in a scalar quantity. Its most important application is in calculating Work Done (W = F ⋅ d), where work is the dot product of force and displacement vectors. It is also used to find the angle between two vectors.
- Cross Product (Vector Product): Represents a vector that is perpendicular to the plane containing the two original vectors. It results in a vector quantity. Key applications include calculating Torque (τ = r × F) and Angular Momentum (L = r × p). It is also used to find the area of a parallelogram or triangle formed by two vectors.

























