CBSE Class 11 Physics Chapter 6 Important Questions - Free PDF Download
Physics Class 11 Chapter 6 Important Questions PDF provides a detailed insight into the chapter with the help of problem-solving methods. Chapter 6 of Physics Class 11 deals with the system of particles and rotational motion. Students who are aiming for CBSE board exams or any competitive exams, entrance exams must prepare thoroughly with the help of Important Questions For Class 11 Physics Chapter 6 PDF available on the Vedantu website.
Students who want to secure good grades in the examinations must refer Physics Class 11 Important Questions from the Vedantu website. Chapter 6 Physics Class 11 Important Questions study material prepared by the experts and the master teachers in such a way that the study material incorporates every subtopic of the Chapter 6 system of particle and rotational motion and Class 11 Physics rotational motion important questions will help students who are seeking for practice questions.
Study Important Questions for Class 11 Physics Chapter 6 - System of Particles and Rotational Motion
Very short answer questions (1 Mark)
1. A wheel
Ans: Angular speed can be given as
2. State the condition for translational equilibrium of a body.
Ans: For a body to be in a translational equilibrium, the vector sum of all the forces acting on the body must be equal to zero.
3. How is angular momentum related to linear momentum?
Ans: Angular momentum can be related as
Or
Where
4. What is the position of the centre of mass of a uniform triangular lamina?
Ans: The centre of mass of a uniform triangular lamina is at the centroid of the triangular lamina.
5. What is the moment of inertia of a sphere of mass
Ans:
6. What are the factors on which moment of inertia of a body depends?
Ans: Moment of inertia of a body depends on:
Mass of the body
Shape and size of the body
Position of the axis of rotation
7. Two particles in an isolated system undergo head on collision. What is the acceleration of the centre of mass of the system?
Ans: Acceleration of the centre of mass of the system is zero.
8. Which component of a force does not contribute towards torque?
Ans: The component of a force that does not contribute towards torque is the radial component.
9. What is the position of centre of mass of a rectangular lamina?
Ans: The point of intersection of diagonal is the position of the centre of mass of a rectangular lamina.
10. Give the location of the centre of mass of a
sphere,
cylinder,
ring, and
cube, each of uniform mass density.
Does the centre of mass of a body necessarily lie inside the body?
Ans: The centre of mass (C.M.) can be defined as a point where the mass of a body is supposed to be concentrated.
For the above listed geometric shapes having a uniform mass density, the centre of mass lies at their respective geometric centres.
The centre of mass of a specific body need not necessarily lie inside of the body. For example, the centre of mass of bodies such as a ring, a hollow sphere, etc., lies outside the respective body.
11. A child sits stationary at one end of a long trolley moving uniformly with a speed
Ans: There will not be any change in the speed of the centre of mass of the given system. The child is running arbitrarily on a trolley that is moving forward with velocity
Internal forces in a body produce no effect on the motion of the bodies on which they are acting. Because there is no external force involved in the (child + trolley) system, the child’s motion will not produce any change in the speed of the centre of mass of the trolley.
12. To maintain a rotor at a uniform angular speed of
Ans: Angular speed of the rotor is given as,
Torque required by the rotor of the engine is given as
The power of the rotor
Therefore, the power required by the engine is
Short Answer Questions (2 Marks)
1. A planet revolves around on massive star in a highly elliptical orbit is its angular momentum constant over the entire orbit. Give reason?
Ans: When a planet revolves around the star, it takes place under the effect of gravitational force. The force is radial and does not contribute towards torque. Hence, in the absence of an external torque angular momentum of the planet remains constant.
2. Obtain the equation
Ans: We know the relation,
Integrating within the limits
Hence, proved.
3. What is the torque of the force
Ans: Torque is given by
4. What is the value of linear velocity if
Ans: Linear velocity is given by
5. Establish the third equation of rotational motion
Ans: We have the relation,
Multiply and divide by
Integrating we get
Hence, proved.
6. Find the expression for radius of gyration of a solid sphere about one of its diameters.
Ans: Moment of inertia of a solid sphere about its diameter can be given as,
7. Prove that the centre of mass of two particles divides the line joining the particles in the inverse ratio of their masses?
Ans: We can express the relation as
If centre of mass is at the origin,
In terms of magnitude, it can be expressed as,
8. Show that cross product of two parallel vectors is zero.
Ans:
If
Then,
9. Prove the relation
Ans: We are aware of the relation,
Differentiating on both sides with respect to time
Where,
And
From (1) and (2)
Hence, proved.
10. Show that for an isolated system the centre of mass moves with uniform velocity along a straight line path.
Ans: For the given conditions let
For an isolated system it can be given as,
Or
11. The angle
at time
Ans: In the question it is given that
Now, Angular velocity
At
Again, angular acceleration can be given as,
At
12. A solid cylinder of mass
Ans: Mass of the cylinder is given as,
Angular speed is given as,
Radius of the cylinder,
The moment of inertia of the solid cylinder can be given as:
Now,
Kinetic energy can be given as:
Angular momentum can be given as,
13. A rope of negligible mass is wound round a hollow cylinder of mass
Ans: Given that,
Mass of the hollow cylinder is given as,
Radius of the hollow cylinder is given as,
Applied force on the given rope is given as,
The moment of inertia of the hollow cylinder about its geometric axis can be given as:
Torque acting on the rope,
For angular acceleration
Linear acceleration of the rope can be stated as
14. A bullet of mass
Ans: Given that,
Mass of the bullet is given as,
Velocity of the bullet is given as,
Width of the door,
Radius of the door,
Mass of the door is given,
Angular momentum transmitted by the bullet on the door:
Moment of inertia of the door can be given as:
But we have the relation,
15. Explain why friction is necessary to make the disc in Fig. 7.41 roll in the direction indicated.
(a). Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
Ans: To roll the given disc, some torque is necessary. As per the definition of torque, the rotating force must be tangential to the disc. Since the frictional force at point
Force of friction will act in the opposite direction to the direction of velocity at point
(b). What is the force of friction after perfect rolling begins?
Ans: Since frictional force will act opposite to the direction of velocity at point
Long Answer Questions (3 Marks)
1. The moment of inertia of a solid sphere about a tangent is
Ans: From the diagram we can infer that a tangent
Then according to Theorem of parallel axis,
M.I about the tangent can be given as
2. Four particles of mass
Ans: From the given data we can infer,
Now,
Therefore, the centre of mass is located at
3. A circular ring of diameter
Ans: From the question we can write,
Now, Moment of inertia can be calculated as,
Angular momentum can be calculated as,
4.
(a). Which physical quantities are represented by the
(i) Rate of change of angular momentum?
Ans: Torque i.e.,
(ii) Product of
Ans: Angular momentum i.e.,
(b). Show that angular momentum of a satellite of mass
Ans: Given that
Mass of satellite is given as
Mass of earth is given as
Radius of satellite is given as
Required centripetal force can be given as
Where
Now, Gravitational force between the satellite and the earth can be given as:
Equating equations (1) and (2)
Now angular momentum of the satellite can be given as,
Hence, proved
5. In the
Ans: The provided situation can be expressed as:
Distance between
Mass of
Mass of
Let the centre of mass of the given system be at a distance
Distance between the centre of mass and the
Let us suppose that the centre of mass of the given molecule lies at the origin. Therefore, it can be written as:
Here, the negative sign gives an indication that the centre of mass lies at the left side of the molecule.
Therefore, the centre of mass of the
6. Show that the area of the triangle contained between the vectors
Ans: Let us consider two vectors
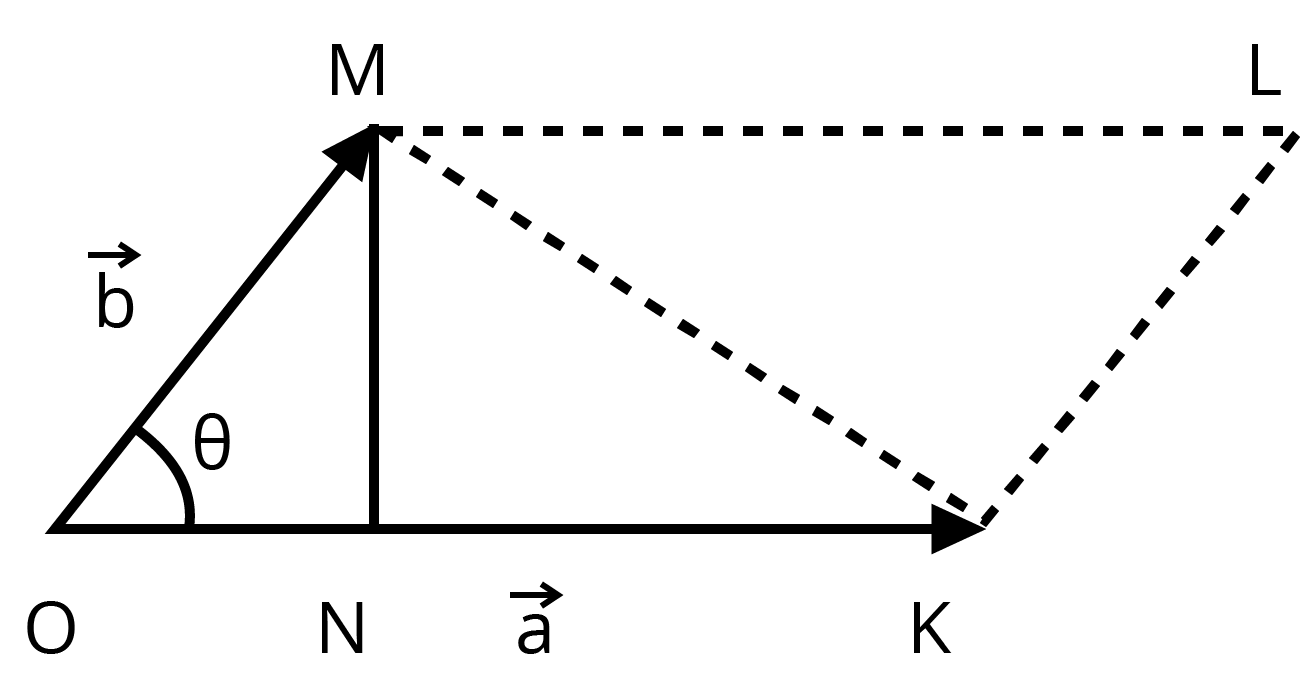
In
Now,
7. A meter stick is balanced on a knife edge at its centre. When two coins, each of mass
Ans: Let us assume that
The mass of the meter stick is supposed to be concentrated at its mid-point, i.e., at the
Mass of the meter stick is
Mass of each coin is
When the coins are placed
The net torque will be thus conserved for rotational equilibrium about point
This can be expressed by the equation,
Therefore, the mass of the meter stick is
Long Answer Questions (4 Marks)
1. Show that
Ans: A parallelepiped with origin
Volume of the given parallelepiped
And
Let us suppose that
Now,
2. A hoop of radius
Ans: Given that,
Radius of the hoop is given as,
Mass of the hoop is,
Velocity of the hoop is,
Total energy of the hoop
Moment of inertia of the hoop about its centre can be given as
But we have the formula,
The work needed to be done for halting the hoop is same to the total energy of the hoop.
Hence, required work to be done can be given as,
3. The oxygen molecule has a mass of
Ans: Given that,
Mass of an oxygen molecule is given as,
Moment of inertia of oxygen molecule is given as,
Velocity of the oxygen molecule is given as,
Let the separation between the two atoms of the oxygen molecule be
Mass of each oxygen atom in the oxygen molecule
Therefore, moment of inertia
It is provided that:
4. A man stands on a rotating platform, with his arms stretched horizontally holding a
(a). What is his new angular speed? (Neglect friction.)
Ans: Moment of inertia of the man-platform system is given as,
Moment of inertia when the man stretches his hands to a distance of 90 cm:
Initial moment of inertia of the system can be given as,
Angular speed can be expressed as,
Angular momentum can be given as,
Moment of inertia when the man folds his hands to a distance of 20 cm becomes:
Final moment of inertia is given as,
Final angular speed can be given as,
Final angular momentum can be expressed as,
From the conservation of angular momentum, we can write:
(b). Is kinetic energy conserved in the process? If not, from where does the change come about?
Ans: Kinetic energy is not conserved in the mentioned process. With the decrease in the moment of inertia, there is an increase in kinetic energy. The additional kinetic energy is generated from the work done by the man to fold his hands toward himself.
5. Read each statement below carefully, and state, with reasons, if it is true or false;
(a). During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
Ans: False
Frictional force acts in the opposite direction of motion of the centre of mass of a body. In the case of rolling, the direct point of motion of the centre of mass is in backward direction. Therefore, frictional force acts in the forward direction.
(b). The instantaneous speed of the point of contact during rolling is zero.
Ans: True
Rolling can be considered as the rotation of a body about an axis that passes through the point of contact of the body with the ground. Therefore, its instantaneous speed is zero.
(c). The instantaneous acceleration of the point of contact during rolling is zero.
Ans: False
When a body is rolling, its instantaneous acceleration is not equal to zero. It has some value.
(d). For perfect rolling motion, work done against friction is zero.
Ans: True
When perfect rolling begins, the frictional force that acts at the lowermost point becomes zero. Therefore, the work done against friction is also zero.
(e). A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
Ans: True.
The rolling of a body occurs when a frictional force will act between the body and the surface. This frictional force will give the torque necessary for rolling. When the frictional force is not present, the body slips from the inclined plane under the effect of its own weight.
6. Two particles, each of mass
Ans: Let us suppose that at a certain instant two particles be at points
Angular momentum of the system about point
Angular momentum of the system about point Q can be given as:
Let us consider a point
Angular momentum of the system about point
On comparing equations (1), (2), and (3), we get:
We can hence infer from equation (4) that the angular momentum of a system is independent on the point about which it is taken.
Very Long Answer Questions (5 Marks)
1.
(a). Why is moment of inertia called rotational inertia?
Ans: Rotational inertia measures the moment of inertia during its rotational motion. Clearly, the moment of inertia is called rotational inertia.
(b). Calculate M.I of a uniform circular disc of mass
(i) Diameter
Ans: Moment of inertia can be given as:
(ii) axis tangent to the disc and parallel to diameter
Ans: Moment of inertia can be given as:
(c). Axis passing through centre and perpendicular to its plane?
Ans: Moment of inertia can be calculated:
2.
(a). A cat is able to land on its feet after a fall. Why?
Ans: When cat lands to the ground, it stretches its tail as a result of which, the moment of inertia increases.
Also,
Angular speed will be small because increase in moment of inertia and thus, the cat is able to land on its feet without any harm.
(b). If angular momentum moment of inertia is decreased, will its rotational be also conserved? Explain.
Ans: The moment of inertia of a system decreases from
Then the angular speed will increase from
We can write,
Since,
K.E. of rotation of the system can be given as
Therefore, because
3. Find the components along the
Ans: Linear momentum of the particle,
Position vector of the particle,
Angular momentum,
Now,
On comparing the coefficients of
The particle is moving in the x-y plane. Therefore, the z-component of the position vector and linear momentum vector is becoming zero, i.e.,
Thus, equation (1) reduces to:
Hence, when the particle is subject to move in the x-y plane, the direction of angular momentum will be along the z-direction.
4. A non-uniform bar of weight
Ans: The free body diagram of the bar can be drawn as shown in the given figure.
Length of the bar is given,
At translational equilibrium, we can express:
On taking the torque about the centre of gravity, for rotational equilibrium, we can write:
Therefore, the centre of gravity of the given bar lies
5. A car weighs
Ans: Given that,
Mass of the car is given as,
Distance between the front and back axles,
Distance between the centre of gravity and the back axle
The different forces acting on the car are shown in the given figure:
The forces in the figure,
At translational equilibrium we can write:
For rotational equilibrium, on taking the torque about the centre of gravity, we can write:
Solving equations (1) and (2), we obtain:
Therefore, the force exerted on each front wheel can be given as
the force exerted on each back wheel can be given as
6.
(a). Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be
Ans: The moment of inertia (M.I.) of a sphere about its diameter can be given as:
According to the theorem of parallel axes, the moment of inertia of a body about any axis is same as the sum of the moment of inertia of a certain body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
The moment of inertia about a tangent of the sphere can be expressed as:
(b). Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be
Ans: The moment of inertia of a disc about its diameter can be given as:
We can infer that, according to the theorem of perpendicular axis, the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is same as the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body.
The moment of inertia of the disc about its centre is
The position of the perpendicular axis is shown in the following figure.
On application of the theorem of parallel axes:
The moment of inertia about an axis normal to the disc and passing through a point on its edge is
7. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Ans: Let us assume that
The moment of inertia of the solid sphere about an axis that passes through its centre can be given as,
The formula for torque in terms of angular acceleration and moment of inertia can be expressed as:
Where,
For the hollow cylinder the expression can be given as,
For the solid sphere the expression can be given as,
As an equal amount of torque is applied to both the bodies it can be stated as,
Using the relation
Where,
For equal
From equations (1) and (2), we can conclude:
Therefore, the angular velocity (
8.
(a). A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of
Ans: Given that,
Initial angular velocity of turntable,
Final angular velocity of the given turntable is
The moment of inertia of the child with stretched hands can be given as
The moment of inertia of the child with folded hands can be given as
The two moments of inertia are related to each other as follows:
Since no external force acts on the child, the angular momentum
Therefore, for the two circumstances, we can write:
(b). Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
Ans: Given that,
Initial Kinetic energy of rotation of the turntable,
Final kinetic energy of rotation of the turntable,
The increase in the rotational kinetic energy is related to the internal energy of the boy on the turntable.
9. From a uniform disc of radius
Ans: Mass per unit area of the original disc can be given as
Radius of the original disc
Mass of the original disc,
The disc with the cut portion is shown in the given figure:
Radius of the smaller disc is given
Mass of the smaller disc is given as
Let us suppose that
It is provided that:
After the smaller disc has been cut from the original disc, the remaining portion left over after cutting is considered to be a system of two masses. The two masses can be expressed as:
(The negative sign in the above statement indicates that this portion has been removed from the original disc.)
Let us suppose that
The relation between the centres of masses of two masses is given as:
For the given system, it can be written as:
(The negative sign in the above statement indicates that the centre of mass gets shifted toward the left of point
The centre of gravity of the resulting flat body can be located from the original centre of the body and opposite to the centre of the cut portion.
10. A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination.
(a). Will it reach the bottom with the same speed in each case?
Ans: Mass of the sphere
Height of the plane
Velocity of the sphere at the bottom of the plane is given as
At the top of the plane, the total energy of the sphere i.e., Potential energy
At the bottom of the plane, the sphere has both translational and rotational kinetic energies which can be expressed as,
Therefore, total energy
Using the law of conservation of energy, we can state that:
For a solid sphere, the moment of inertia about its centre can be given as,
Therefore, equation (1) becomes:
But we have the formula,
Therefore, the velocity of the sphere at the bottom depends only on height (h) and acceleration due to gravity (g). Both values are constants and do not change. Therefore, the velocity at the bottom remains the same from whichever inclined plane the sphere is rolled.
(b). Will it take longer to roll down one plane than the other?
Ans: Let us consider two inclined planes with inclinations
The acceleration generated in the sphere when it rolls down the plane inclined at
The different forces acting on the sphere are shown in the given figure.
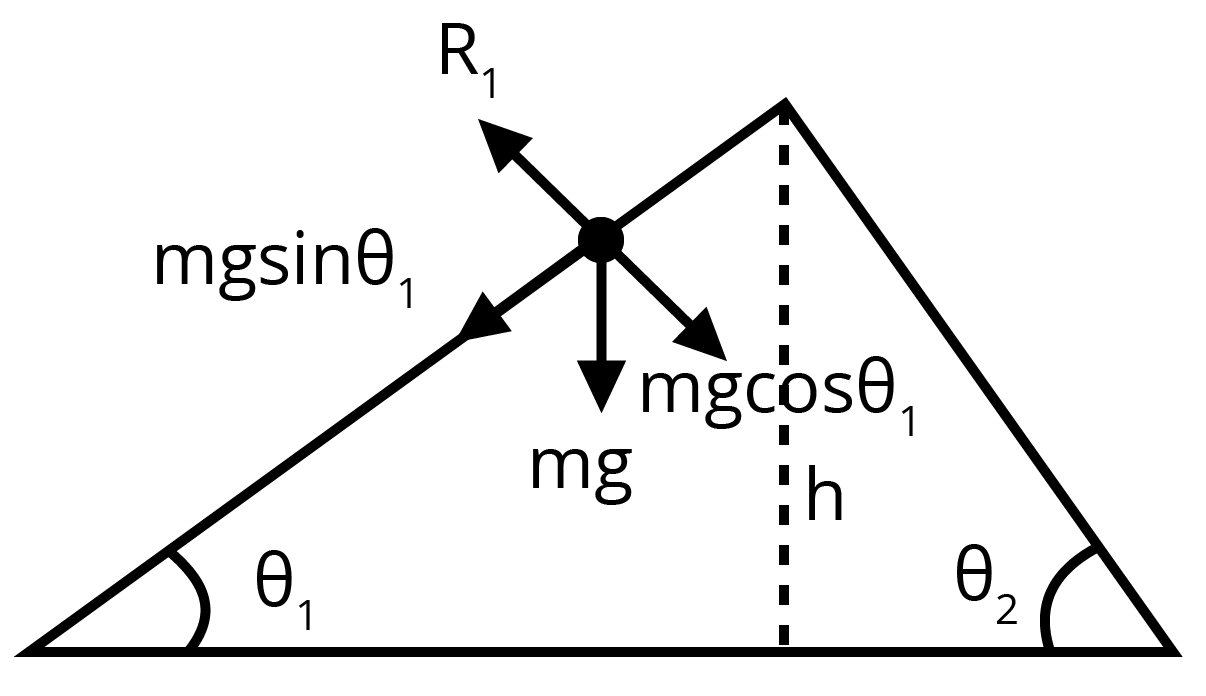
Here,
Similarly, the acceleration generated in the sphere when it rolls down the plane inclined at
The different forces that act on the sphere are shown in the given figure.
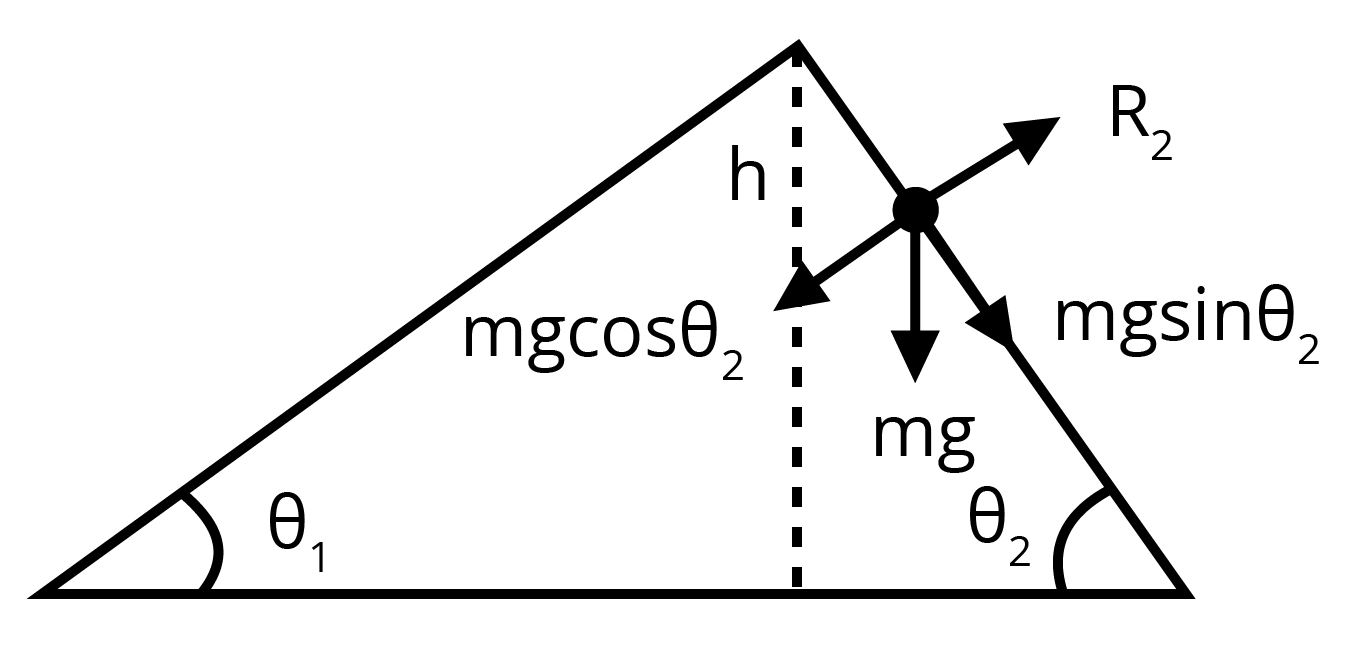
Initial velocity of sphere,
Final velocity of sphere,
Now, by using the first equation of motion, we can obtain the time of roll as:
For inclination of angle
For inclination of angle
(c). If so, which one and why?
Ans: From equations (2) and (3), we obtain:
Therefore, conclude that the sphere will take a longer time to reach the bottom of the inclined plane having the smaller inclination.
11. A solid cylinder rolls up an inclined plane of angle of inclination
How long will it take to return to the bottom?
Ans: A solid cylinder rolling up an inclination is pictured in the following figure.
Initial velocity of the solid cylinder on the inclined plane,
Angle of inclination is
Height reached by the cylinder on the inclined plane
Energy of the cylinder on the inclined plane at point
Energy of the cylinder at point
Let us use the law of conservation of energy, we can express:
Moment of inertia of the solid cylinder is
But we have the expression,
In
Therefore, the cylinder will move
For radius of gyration
For the solid cylinder we can write
The time taken to return to the bottom can be given as:
Therefore, the total time taken by the cylinder to return to the bottom is
12. As shown in figure, the two sides of a step ladder
(Hint: Consider the equilibrium of each side of the ladder separately.)
Ans: The given situation can be depicted as follows:
Mass of the given weight,
Draw a perpendicular line from
In
Therefore,
It can be said that
Therefore, we can express:
Using equations (1) and (2), we get:
Therefore,
In
For translational equilibrium of the ladder, the upward force should be the same as the downward force.
For rotational equilibrium of the ladder, the net moment about A can be given as:
Solving equations (3) and (4), we can write:
For rotational equilibrium of the side AB, let us consider the moment about A.
13. Two discs of moments of inertia
(a). What is the angular speed of the two-disc system?
Ans: Given that,
Moment of inertia of disc 1 is
Angular speed of disc 1 is
Moment of inertia of disc 2 is
Angular speed of disc 2 is
Angular momentum of disc 1 is
Angular momentum of disc 2 is
Total initial angular momentum is
When the two discs are joined together, their moments of inertia get summed up.
Moment of inertia of the system of two discs can be given as,
Let
Total final angular momentum is given as,
Let us use the law of conservation of angular momentum,
(b). Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take
Ans: Given that,
Kinetic energy of disc 1 is given as,
Kinetic energy of disc 2,
Total initial kinetic energy can be given as,
When the discs are joined, their moments of inertia get summed up.
Moment of inertia of the system can be given as,
Angular speed of the system can be given as:
Final kinetic energy
And
All the quantities on right hand side are positive
The loss of K.E. can be attributed to the frictional force that comes into play when the two discs come in contact with each other.
14.
(a). Prove the theorem of perpendicular axes. (Hint: Square of the distance of a point
Ans: It is stated by the theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body.
A physical body with centre
Moment of inertia about x-axis can be given as,
Moment of inertia about y-axis can be given as,
Moment of inertia about z-axis can be given as,
Therefore, the theorem is proved.
(b). Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin
Ans: The theorem of parallel axes states that the moment of inertia of a body about any axis is same as the sum of the moment of inertia of the body about a parallel axis that passes through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Let us suppose that a rigid body is made up of
The moment of inertia about axis
The perpendicular distance of mass
Therefore, the moment of inertia about axis
Now, at the centre of mass, the moment of inertia of all the particles about the axis that passes through the centre of mass is zero, that is,
Where,
Therefore, the theorem is proved.
15. Prove the result that the velocity
Ans: A body rolling on an inclined plane of height h, is depicted in the given figure:
Total energy at the top of the plane is given as,
Total energy at the bottom of the plane can be given as,
But
From the law of conservation of energy, we can write:
Therefore, the given result is proved.
16. A disc rotating about its axis with angular speed
Ans: From the question we can infer that:
The rolling of the disc will not take place.
Angular speed of the disc is given
Radius of the disc is given
Let us use the relation for linear velocity,
For point A we can write:
For point B we can write:
For point C it can be written as:
The directions of motion of points
Because the disc is placed on a frictionless table, the disc will not roll. This is due to the presence of friction, which is essential for the rolling of a body.
17. A solid disc and a ring, both of radius
Ans: Given that,
Radii of the ring and the disc are given as, r = 10 cm = 0.1 m
Initial angular speed is given,
Coefficient of kinetic friction is,
Initial velocity of both the objects,
Motion of the two objects is a result of frictional force. As per Newton’s second law of motion,
we have frictional force,
Where,
From the first equation of motion, the final velocity of the objects can be obtained as:
The torque applied by the frictional force will act in perpendicularly outward direction and cause reduction in the initial angular speed.
Torque,
Let us use the first equation of rotational motion to obtain the final angular speed:
Rolling starts when linear velocity,
Equating equations (2) and (5), we can write:
For the ring:
For the disc:
Since,
18. A cylinder of mass
(a). How much is the force of friction acting on the cylinder?
Ans: Given that,
Mass of the cylinder is given as,
Radius of the cylinder is given as,
Co-efficient of kinetic friction
Angle of inclination is given as,
Moment of inertia of a solid cylinder about its geometric axis is,
The various forces acting on the cylinder are depicted in the given figure:
The acceleration of the cylinder is given as:
Let us use Newton’s second law of motion, we can express net force as:
(b). What is the work done against friction during rolling?
Ans: During rolling, the instantaneous point of contact with the plane will come to rest. Therefore, the work done against frictional force will be zero.
(c). If the inclination of the plane is increased, at what value of does the cylinder begin to skid, and not roll perfectly?
Ans: For rolling without skidding, we have the formula:
19. Separation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a). Show
Ans: Let us take a system of
Mass of the
Velocity of the
Therefore, momentum of the
Velocity of the centre of mass is
The velocity of the
Multiplying
we can write:
Where,
Hence,
We have the formula:
Taking the summation of momentum of all the particles with respect to the centre of mass of the system, we can write:
Where
As per the definition of the centre of mass, we have:
(b). Show
Ans: We have the formula for velocity of the
Taking the dot product of equation (2) with itself, we can write:
Now, for the centre of mass of the system of particles,
Where,
(c). Show
Ans: Position vector of the
Position vector of the
With respect to the origin the position vector of the centre of mass
It is provided that:
We have the following relation from part (a),
Taking the cross product of this relation by
where,
Hence,
(c). Show
Ans: We have the following relation:
Where,
We have the following relation:
Where,
Therefore, according to Newton’s third law of motion, we can express:
Hence,
Download Important Questions For Class 11 Physics Chapter 6 PDF
Physics Class 11 Chapter 6 Important Questions
Chapter 6 system of particles and rotational motion is one of the important concepts to be learned in Class 11 Physics. The system of particles and rotational motion is one of those chapters where it requires a lot of imagination for understanding the concepts. Before starting with Physics Class 11 Chapter 6 important questions, students must have a great hold on the chapter. By now students must be well versed with concepts like the definition of rotational motion, rigid bodies, centre of mass system, etc.
Students can boost their preparation with Class 11 Physics Chapter 6 extra questions which will enable them to solve maximum questions and with answers. The system of particles and rotational motion chapter includes various important topics that will enhance the knowledge of rigid body motion with illustrations from the objects we witness to observe in our everyday life.
Class 11 Physics Rotational Motion Important Questions
Every object we see in our life has a finite structure, we know that rigid bodies are those in which the distance between the particles will remain constant. A rigid body fixed at the point will be only allowed to execute the rotational motion. A free rigid body will be either having a translational motion or both translational and rotational motion.
There are some important topics that will lead to earning good grades in the board exams or in any entrance examinations. Some of the key points of the chapter are as follows:
Determining the motion of rigid bodies, the centre of mass of the system.
Finding the density of the body depending upon the type of distribution of particles. The distribution of the particles will be either discrete or continuous systems.
Introducing the concept of torque. Explanation and effect of torque on the rigid bodies.
Rotational motion visualization, explaining conservation laws, etc.
Like these, we come across several interesting topics under Chapter 6 of Class 11 Physics. For a detailed understanding of the concepts, students must practice Chapter 6 Physics Class 11 important questions. The only key to master any subject is constant determination and practising every day. The detailed revision notes, chapter-wise materials, important questions, etc. are available on the Vedantu website in the PDF form and students can download them anytime.
Conclusion
Vedantu’s Important Questions for CBSE Class 11 Physics Chapter 6 - "Systems of Particles and Rotational Motion" serves as a crucial asset for students. These questions are strategically designed to cover vital concepts and fundamental principles related to rotational dynamics. They offer students a targeted approach to exam preparation, helping them identify key areas of focus and providing an opportunity for self-assessment. By mirroring the examination pattern and difficulty level, these important questions enable students to build confidence and proficiency in the subject. Overall, they are an invaluable resource that empowers Class 11 Physics students to excel in their studies and perform exceptionally well in their exams.
Related Study Materials for Class 11 Physics Chapter 6
S.No | Important Other Links for Class 11 Physics Chapter 6 |
1. | CBSE Class 11 Systems of Particles and Rotational Motion Notes |
2. | CBSE Class 11 Systems of Particles and Rotational Motion Solutions |
CBSE Class 11 Physics Chapter-wise Important Questions
CBSE Class 11 Physics Chapter-wise Important Questions and Answers cover topics from other chapters, helping students prepare thoroughly by focusing on key topics for easier revision.
S.No | Chapter-wise Important Questions for Class 11 Physics |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 |
Additional Study Materials for Class 11 Physics
S.No. | Study Materials for Class 11 Physics |
|---|---|
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 |
Vedantu is one of the leading online learning websites available. Many students have benefited from the free material available on the Vedantu platform. Register today for the Vedantu and have access to many more extended study materials for boosting your preparation.
FAQs on Important Questions for CBSE Class 11 Physics Chapter 6 - Systems of Particles and Rotational Motion
1. Is Chapter 6-Work, Power, and Energy of Class 11 Physics difficult?
Chapter 6-Work, Power, and Energy of Class 11 Physics is an important chapter from the exam's point of view. Students find this chapter difficult because there are many different concepts given in the chapter. Students have to learn the formulae, solve the numerical, and understand the definitions given in this chapter for scoring high marks in CBSE exams. Students can score high marks by practising important questions available on Vedantu app and website. Students can visit Vedantu to download PDFs of important questions free of cost.
2. Do I have to learn the definitions given in Chapter 6 of Class 11 Physics?
Yes, students have to learn important definitions in Class 11 Physics Chapter 6 and can understand all the basic concepts easily. They can download the important definitions and important questions from Vedantu and can prepare for their exams effortlessly by preparing short notes. Important questions for Class 11 Physics Chapter 6 are prepared by expert and qualified teachers to help students understand the concepts easily.
3. What are the important topics given in Chapter 6-Work, Power, and Energy of Class 11 Physics?
Important topics covered in Chapter 6 of Class 11 Physics include an introduction, the theorem related to work, energy, and power, different types of energies such as kinetic energy, potential energy, and mechanical energy. Students will also learn the concept of conservation of energy and laws related to the conservation of energy. Students can understand all important topics given in Class 11 Physics Chapter 6 by practicing important questions given on Vedantu.
4. How important is Class 11 Physics Chapter 6 for JEE and NEET Exams?
Class 11 Physics Chapter 6 is very important for JEE and NEET exams. Students should understand the basic concepts of this chapter to score high marks in the board exams and entrance exams. They should practice formulas and numerical for solving numerical problems. Students can get high marks in the board exams and entrance exams.
5. Where can I find Important Questions for Class 11 Physics Chapter 6 Work, Energy and Power?
Vedantu offers a well-prepared set of Important Questions for all subjects. Our experts select questions based on the exam pattern and questions from the previous papers. These questions are solved by subject matter experts to provide a thorough understanding of the Class 11 Physics Chapter 6 Work, Energy and Power with step by step solutions.























