CBSE Class 11 Physics Chapter 7 Important Questions - Free PDF Download
1 Mark Questions
1. Why is Gravitational Potential Energy Always Negative?
Ans: Gravitational force is always attractive because of which gravitational potential energy is always negative.
2. At What Height Above the Surface of the Earth, the Value of Acceleration Due to Gravity is Reduced to One Fourth of Its Value on the Surface of the Earth?
Ans: Given,
\[{{g}_{h}}=\frac{g}{4}\]
As we know, gravity at some height is given by:
\[{{g}_{h}}=g{{\left( \frac{R}{R+h} \right)}^{2}}\]
\[\Rightarrow \frac{g}{4}=g{{\left( \frac{R}{R+h} \right)}^{2}}\]
\[\Rightarrow \frac{R}{R+h}=\frac{1}{\sqrt{4}}=\frac{1}{2}\]
\[\Rightarrow 2R=R+h\]
\[\Rightarrow 2R-R=h\]
\[\Rightarrow h=R\]
At height \[R\] above the surface of the earth, the value of acceleration due to gravity is reduced to one fourth of its value on the surface of the earth.
3. Name Two Factors Which Determine Whether a Planet has an Atmosphere or Not.
Ans: The factors that determine whether a planet has atmosphere or not are:
Acceleration due to gravity at the planet's surface.
Planet’s surface temperature.
4. The Gravitational Force Between Two Blocks is $F$. What Would Happen If the Mass of Both the Blocks as Well as Distance Between Them Is Doubled?
Ans: We know that the gravitational force is given by the following expression:
\[F=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
Here, the mass and distance between the two blocks are doubled i.e., \[{{m}_{1}}={{m}_{2}}=2m\]
\[{{r}_{1}}={{r}_{2}}=2r\]
We use the force of gravitation formula,
\[F=\frac{G(2m)(2m)}{4{{r}^{2}}}=\frac{G{{m}^{2}}}{{{r}^{2}}}\]
Force will remain the same when the mass of both the blocks as well as the distance between them is doubled.
5. A Body is Weightless at the Centre of Earth. Why?
Ans: At the centre of the earth, \[g=0\].
Weight is given by:
\[w=mg\]
$\Rightarrow w=0$
Therefore, the body is weightless at the centre of earth.
6. Where Will a Body Weigh More? At Delhi or at Shimla? Why?
Ans: The value of acceleration due to gravity decreases at higher altitudes, due to which a body will weigh more at Delhi.
7. On Which Fundamental Law of Physics is Kepler’s Second Law Based?
Ans: The law of conservation of angular momentum is based on Kepler’s second law.
8. Which is Greater? The attraction of the earth for \[1\text{ }kg\] of aluminium or attraction of \[1\text{ }kg\] of aluminium for the earth?
Ans: Both the forces are equal and opposite by the universal law of gravitation.
9. The Distance Between Two Bodies is Increased to Three Times Its Original Value. What Is the Effect on the Gravitational Force Between Them?
Ans: Since, we know that the gravitational force is inversely proportional to the square of the distance between the two bodies, i.e.,
\[F\propto \frac{1}{{{r}^{2}}}\]
Now, the distance between the two bodies is increased to three times its original value, i.e.,
\[r'\to 3r\]
\[\therefore \] Force will be increased by \[\frac{1}{9}\] times.
10. Choose the Correct Alternative:
A. If the Zero of Potential Energy is at Infinity, the Total Energy of an Orbiting Satellite is Negative of Its Kinetic / Potential Energy.
Ans: Kinetic energy.
The sum of kinetic energy and potential energy is the total mechanical energy. The satellite's gravitational potential energy is zero at infinity. As we know, the Earth-satellite system is a bound system; then, the satellite's total energy is negative.
Thus, at infinity, the orbiting satellite's total energy is equal to the negative of its kinetic energy.
B. The Energy Required to Launch an Orbiting Satellite Out of Earth's Gravitational Influence Is More/less Than the Energy Required to Project a Stationary Object at the Same Height (as the Satellite) Out of Earth's Influence.
Ans: Less.
An orbiting satellite gets a certain amount of energy that permits it to rotate around the Earth. Its orbit gives this energy. It requires comparatively less energy to go out of the influence of the Earth's gravitational field than a fixed object on the Earth's surface that initially holds no energy.
2 Marks Questions
1. What Is Kepler’s Law of Periods? Show it Mathematically.
Ans: Kepler’s law of period says that the square of the period of the planet's revolution around the sun is proportional to a planet to the cube of the semi-major axis of the elliptical path.
i.e.,
\[{{T}^{2}}\propto {{R}^{3}}\]
\[{{T}^{2}}=K{{R}^{3}}\]
Where,\[T\] is the time period of evolution
\[R\] is the length of semi major axis
\[K\] is constant for all planets.
2. Write Two Characteristics of Gravitational Force.
Ans: The characteristics of gravitational force are:
Gravitational force is a central force and is always attractive.
It is a conservative force and a universal force.
It follows inverse square law.
3. Assuming Earth to be a Uniform Sphere, Find an Expression for the Density of Earth in terms of \[g\] and \[G\].
Ans: The formula for acceleration due to gravity is given by:
\[g=\frac{GM}{{{R}^{2}}}\]
Earth is a uniform sphere and its density is \[\rho \], then acceleration due to gravity will be,
\[g=\frac{G}{{{R}^{2}}}\left( \frac{4}{3}\pi {{R}^{3}}\rho \right)\]
\[\Rightarrow g=\frac{4}{3}\pi GR\rho \]
\[\Rightarrow \rho =\frac{3g}{4\pi GR}\]
Therefore, the density of earth in terms of g and G is given by the above equation.
4. If the radius of earth is \[6400km\], what will be the weight of \[\text{1 quintal}\] body if taken to the height of \[1600km\] above the sea level?
Ans: Given:
Radius of earth, \[R=6400km\]
\[\Rightarrow R=6400\times {{10}^{3}}m\]
Weight of the body is given by: \[w=mg\]
\[\Rightarrow w=mg=1\text{ quintal}\]
As we know,
\[1\text{ quintal}=100kg\]
Therefore, weight will be,
\[mg=100\times 9.8N\]
Weight at a given height $h$ will be,
\[weight(w)=m{{g}_{h}}\]
Where, \[{{g}_{h}}\] is the gravity at some height $h$ given by \[g{{\left( \frac{R}{R+h} \right)}^{2}}\].
Clearly,
\[w=mg{{\left( \frac{R}{R+h} \right)}^{2}}\]
After putting all the values, we get,
\[w=100\times 9.8{{\left( \frac{6400}{1600+6400} \right)}^{2}}\]
\[\Rightarrow w=64\times 9.8N\]
\[\Rightarrow w=627.2N\]
The weight of $1$ quintal body will be $627.2N$ if taken to a height of $1600km$ above the sea level.
5. The Distance of the Planet Jupiter from the Sun is \[5.2\] times that of the Earth. Find the period of Jupiter's revolution around the sun.
Ans: As we know,
Time period of earth, \[{{T}_{e}}=1year\]
Given the radius of Jupiter, \[{{R}_{J}}=5.2{{\operatorname{R}}_{e}}\]
Here, we can use Kepler’s Third law,
\[{{\left( \frac{{{T}_{J}}}{{{T}_{e}}} \right)}^{2}}={{\left( \frac{{{R}_{J}}}{{{\operatorname{R}}_{e}}} \right)}^{3}}\]
Where, ${{R}_{e}}$ is the radius of the Earth and ${{T}_{J}}$ is the time period of the revolution of Jupiter. Determining ${{T}_{J}}$ using Kepler’s law;
\[\Rightarrow {{\left( \frac{{{T}_{J}}}{1year} \right)}^{2}}={{\left( \frac{5.2{{R}_{e}}}{{{R}_{e}}} \right)}^{3}}\]
\[\Rightarrow {{T}_{J}}^{2}=140.608\times 1year\]
\[\Rightarrow {{T}_{J}}=11.86years\]
The time period of Jupiter will be $11.86years$.
6. Show that for a two particle system, \[{{\vec{F}}_{12}}={{\vec{F}}_{21}}\].
Ans: Consider the figure given below:
Force on body $1$ due to body $2$ is:
\[{{\vec{F}}_{12}}=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}{{\hat{r}}_{21}}......(1)\]
Force on body $2$ due to body $1$ is:
\[{{\vec{F}}_{21}}=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}{{\hat{r}}_{12}}......(2)\]
As \[\left( \hat{r}=\frac{{\vec{r}}}{|\vec{r}|} \right)\], (1) and (2) can be rewritten as:
\[{{\vec{F}}_{12}}=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{3}}}{{\vec{r}}_{21}}\]
\[{{\vec{F}}_{21}}=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{3}}}{{\vec{r}}_{12}}\]
\[\text{Since }{{\vec{r}}_{21}}={{\vec{r}}_{12}}\](Magnitudes of position vectors of masses are equal)
\[\Rightarrow {{\vec{F}}_{21}}=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{3}}}{{\vec{r}}_{21}}\]
\[\Rightarrow {{\vec{F}}_{21}}={{\vec{F}}_{12}}\]
Hence proved.
7. State Two Essential Requisites of a Geostationary Satellite.
Ans: The two essential requisites of a geostationary satellite are:
The period of rotation of a satellite around the earth should be the same as that of earth about its axis.
The sense of satellite rotation should be the same as that of the earth about its axis, that is, from west to east in the anti-clockwise direction.
8. Show That an Artificial Satellite Circling Round the Earth in an Orbit of Radius Obeys Kepler’s Third Law.
Ans: Orbital velocity of a satellite is given by:
\[v=\sqrt{\frac{GM}{r}}\]
Where, \[M\] is the mass of the earth
Time period of the satellite is given by:
\[T=\frac{2\pi r}{v}\]
\[\Rightarrow T=\frac{2\pi r}{\sqrt{\frac{GM}{r}}}\]
\[\Rightarrow T=2\pi \sqrt{\frac{{{r}^{3}}}{GM}}\]
\[\Rightarrow {{T}^{2}}=\frac{4{{\pi }^{2}}{{r}^{3}}}{GM}\]
\[\Rightarrow \frac{4{{\pi }^{2}}}{GM}=R\text{(constant)}\]
\[\text{Thus}\], \[{{T}^{2}}\propto {{r}^{3}}\]
Hence proved.
9. A \[400kg\] satellite in a circular orbit of radius \[2{{\operatorname{R}}_{E}}\] about the earth. Calculate the kinetic energy, potential energy and total energy of the satellite.
\[{{R}_{E}}=6.4\times {{10}^{6}}m\]
\[M=6\times {{10}^{24}}kg\]
Ans: Given that:
Mass of earth, \[M=6\times 1{{0}^{24}}kg\]
Mass of satellite, \[m=400kg\]
Radius of earth, \[{{R}_{E}}=6.4\times {{10}^{6}}m\]
Also,
\[r=2{{R}_{E}}\]
\[r=12.8\times {{10}^{6}}m\]
Gravitational constant, \[G=6.67\times {{10}^{-4}}N{{m}^{2}}k{{g}^{-2}}\]
Kinetic energy, \[KE=\frac{GMm}{2r}\]
\[\Rightarrow \frac{GMm}{2r}=\frac{6.67\times {{10}^{-11}}\times 6\times {{10}^{24}}\times 400}{2(12.8\times {{10}^{6}})}\]
\[\Rightarrow KE=6.25\times {{10}^{9}}joules\]
Potential energy, \[P.E.=\frac{-2GMm}{2r}=-2K.E.\]
\[\Rightarrow P.E.=-2\times 6.25\times {{10}^{9}}=-12.5\times {{10}^{9}}joules\]
Total energy, \[T.E.=K.E.+P.E.\]
\[\Rightarrow T.E.=-6.25\times {{10}^{9}}joules\]
10. Answer the Following:
A. You Can Shield a Charge from Electrical Forces by Putting it Inside a Hollow Conductor. Can You Shield a Body from the Gravitational Influence of Nearby Matter by Putting it Inside a Hollow Sphere or by Some Other Means?
Ans: No.
The gravitational force of matter on nearby objects cannot be eliminated by any means. This is because gravitational force is independent of the nature of the medium's material.
B. An Astronaut Inside a Small Spaceship Orbiting Around the Earth Cannot Detect Gravity. If the Space Station Orbiting Around the Earth Has a Large Size, Can He Hope to Detect Gravity?
Ans: Yes.
If the space station's size is large enough, then the astronaut will identify the change in Earth's gravity.
C. If You Compare the Gravitational Force on the Earth Due to the Sun to That Due to the Moon, You Would Find That the Sun's Pull Is Greater Than the Moon's Pull. (You Can Check This Yourself Using the Data Available in the Succeeding Exercises). However, the Tidal Effect of the Moon's Pull Is Greater Than the Tidal Effect of the Sun. Why?
Ans: The tidal effect depends on the inverse of distance's cube while gravitational force depends on the inverse of distance's square.
Since the distance between the Moon and the Earth is shorter than the distance between the Sun and the Earth, the tidal influence of the Moon's pull is higher than the tidal effect of the Sun's influence.
11. Does the Escape Speed of a Body from the Earth Depend on?
A. The Mass of the Body?
Ans: No.
Escape velocity of a body from the Earth is given by the relation:
\[v=\sqrt{2gR}\]
The escape speed of a body does not depend on the mass of the body.
B. The Location from Where it is Projected?
Ans: No.
Escape velocity of a body from the Earth is given by the relation:
\[v=\sqrt{2gR}\]
The escape speed of a body does not depend on the location from where it is projected.
C. The Direction of Projection?
Ans: No.
Escape velocity of a body from the Earth is given by the relation:
\[v=\sqrt{2gR}\]
The escape speed of a body does not depend on the direction of projection.
D. The height of the location from where the body is launched?
Ans: Yes.
Escape velocity of a body from the Earth is given by the relation:
\[v=\sqrt{2gR}\]
The escape speed of a body does slightly depend on the height of the location from where the body is launched. This is because escape velocity is slightly dependent on the gravitational potential at a certain height.
12. A Comet Orbits the Sun in a Highly Elliptical Orbit. Does the Comet Have a Constant ?
A. Linear Speed?
Ans: No.
The expression for angular momentum is:
$L=\frac{m{{v}^{2}}}{r}$
As angular momentum is constant, linear speed varies as $r$ varies.
B. Angular Speed?
Ans: No.
The expression for angular momentum is:
$L=mw{}^{2}r$
As angular momentum is constant, angular speed varies as $r$ varies.
C. Angular Momentum?
Ans: Yes.
There is no external torque and thus, the angular momentum is constant.
D. Kinetic Energy?
Ans: No.
The expression for kinetic energy is:
$K=\frac{1}{2}m{{v}^{2}}$
Kinetic energy is not constant because linear speed varies.
E. Potential Energy?
Ans: No.
By law of conservation of energy, total energy is constant and it is the sum of potential energy and kinetic energy.
As kinetic energy is not constant, potential energy is also not constant.
F. Total Energy Throughout Its Orbit? Neglect Any Mass Loss of the Comet When it Comes Very Close to the Sun.
Ans: Yes.
By law of conservation of energy, the total energy is constant.
13. As You have Learned in the Text, a Geostationary Satellite Orbits the Earth at a Height of Nearly \[36,000km\] from the Surface of the Earth. What Is the Potential Due to Earth's Gravity at the Site of This Satellite? (take the Potential Energy at Infinity to Be Zero).
Mass of the earth = \[6.0\times {{10}^{24}}kg\],
radius = \[6400km.\]
Ans: Mass of the Earth, \[M=6.0\times {{10}^{24}}kg\]
Radius of the Earth, \[R=6400km=6.4\times {{10}^{6}}m\]
Height of a geostationary satellite from the surface of the Earth,
\[h=36000km=3.6\times {{10}^{7}}m\]
Gravitational potential energy due to Earth’s gravity at height \[h\],
\[PE=\frac{-GM}{(R+h)}\]
\[\Rightarrow PE=-\frac{6.67\times 1{{0}^{-11}}\times 6.0\times {{10}^{24}}}{3.6\times {{10}^{7}}+0.64\times {{10}^{7}}}\]
\[\Rightarrow PE=-\frac{6.67\times 6}{4.24}\times {{10}^{13-7}}\]
\[\Rightarrow PE=-9.4\times {{10}^{6}}Jk{{g}^{-1}}\]
The potential energy due to earth's gravity at the site of this satellite is \[-9.4\times {{10}^{6}}Jk{{g}^{-1}}\].
3 Marks Questions
1. A Satellite Is Revolving in a Circular Path Close to a Planet of Density $\rho $. Find an Expression for Its Period of Revolution.
Ans: If the satellite revolves around the Earth of radius \[r\],
\[T=\frac{2\pi r}{v}\]
Where, \[v\] is orbital velocity given by,
\[v=\sqrt{\frac{Gm}{r}}\]
\[\Rightarrow T=\frac{2\pi r}{v}=\frac{2\pi r}{\sqrt{\frac{Gm}{r}}}\]
\[\Rightarrow T=2\pi \sqrt{\frac{{{r}^{3}}}{Gm}}\]
If a satellite is revolving near the planet’s surface, then, \[r=R\] (radius of planet) and
\[m=\frac{4}{3}\pi {{R}^{3}}\rho \]
\[\Rightarrow T=2\pi \sqrt{\frac{{{R}^{3}}}{G\frac{4}{3}\pi {{R}^{3}}\rho }}\]
\[\Rightarrow T=2\pi \sqrt{\frac{3}{4\pi G\rho }}\]
\[\Rightarrow T=\sqrt{\frac{3\pi }{G\rho }}\]
Thus, the expression for the time period of revolution of the satellite is \[T=\sqrt{\frac{3\pi }{G\rho }}\].
2. How far away from the surface of earth does the value of g be reduced to \[4%\] of its value on the surface of the earth?
Given radius of earth\[=6400km\]
Ans: We know, gravity at height $h$ is given by:
\[{{g}_{h}}=g{{\left( \frac{R}{R+h} \right)}^{2}}\]……(1)
Given:
\[{{g}_{h}}=4%\text{ of }g=\frac{4g}{100}\]……(2)
Radius of earth, \[R=6400km\]
After equating (1) and (2), we get,
\[\frac{4g}{100}=g{{\left( \frac{R}{R+h} \right)}^{2}}\]
\[\Rightarrow \frac{4}{100}={{\left( \frac{R}{R+h} \right)}^{2}}\]
\[\Rightarrow \frac{2}{10}=\frac{R}{R+h}\]
\[\Rightarrow 2R+2h=10R\]
\[\Rightarrow 2h=8R\]
\[\Rightarrow h=4R=4\times 6400\]
\[\Rightarrow h=25,600km\]
Therefore, $25600km$ is the height from the surface of earth when the value of g gets reduced to $4%$ of its value on the surface of the earth.
3. Obtain an Expression Showing Variation of Acceleration Due to Gravity With Height.
Ans: Acceleration due to gravity at the surface of the earth is:
\[g=\frac{GM}{{{R}^{2}}}......(1)\]
Where $G$ is the gravitational constant and $M$ is the mass of the earth.
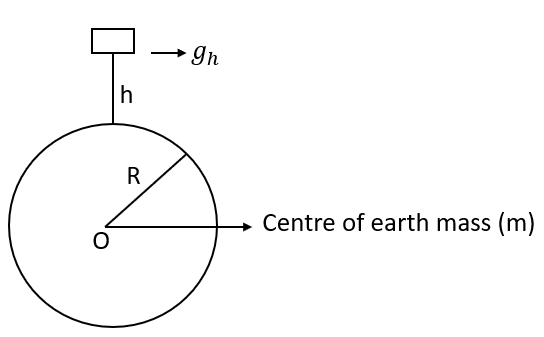
If \[{{g}_{h}}\] is the acceleration due to gravity at a point situated at a height \['h'\] above the surface of the earth,
\[{{g}_{h}}=\frac{GM}{{{(R+h)}^{2}}}\text{ }......(2)\]
\[\text{Divide (2) by (1)}\]
\[\frac{{{g}_{h}}}{g}=\frac{GM}{{{(R+h)}^{2}}}\times \frac{{{R}^{2}}}{GM}\]
\[\Rightarrow \frac{{{g}_{h}}}{g}=\frac{{{R}^{2}}}{{{(R+h)}^{2}}}\]
\[\Rightarrow {{g}_{h}}=g\left( \frac{{{R}^{2}}}{{{(R+h)}^{2}}} \right)\]
If \[h<<<R\text{ }\]then the above relation becomes
\[{{g}_{h}}=g{{\left( 1+\frac{h}{R} \right)}^{-2}}\]
Expanding binomials and neglecting higher power;
\[{{g}_{h}}=g\left( 1-\frac{2h}{R} \right)\]
This is the expression for gravity at a height $h$.
4. Two uniform solid spheres of radii \[R\] and \[2R\] are at rest with their surfaces just touching. Find the force of gravitational attraction between them if the density of spheres is $\rho $.
Ans: The figure having two spheres of density $\rho $ and radii \[R\] and \[2R\] is shown below:
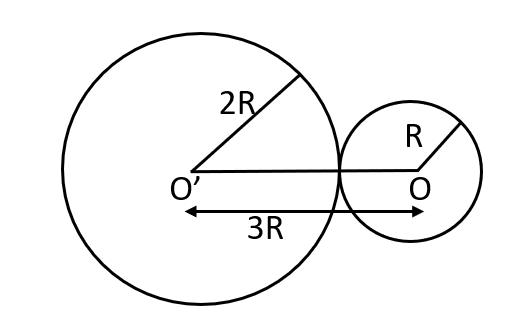
Distance between the spheres:
\[s=OO'\]
\[\Rightarrow s=2R+R=3R\]
Gravitational force is given by:
\[F=\frac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
Where, ${{m}_{1}},{{m}_{2}}$ are the masses of spheres.
$r$ is the distance between two masses.
It is known that for a sphere, density is given by
$\rho =\frac{m}{V}=\frac{m}{\left( \frac{4}{3}\pi {{r}^{3}} \right)}\Rightarrow m=\rho \left( \frac{4}{3}\pi {{r}^{3}} \right)$
Using the above relation, gravitational force can be written as
\[\Rightarrow F=\frac{G\left( \frac{4}{3}\pi \rho {{(2R)}^{3}} \right)\left( \frac{4}{3}\pi \rho {{R}^{3}} \right)}{{{(3R)}^{2}}}\]
\[\Rightarrow F=\frac{128}{27}{{\pi }^{2}}G{{\rho }^{2}}{{R}^{4}}\]
This is the expression for force when $\rho $ is the density of a sphere.
5. For an Artificial Satellite, Find Expressions For-
A. Potential Energy
Ans: Potential energy of a satellite is:
\[U=\int\limits_{\infty }^{r}{F\text{ }dx}\]
Where, $F$ is the force.
\[U=\int\limits_{\infty }^{r}{\frac{GMm}{{{x}^{2}}}dx}\]
Where, M is the mass of earth; m is the mass of the satellite; x is the distance of the satellite from the surface of the earth.
\[\Rightarrow U=GMm\int\limits_{\infty }^{r}{\frac{1}{{{x}^{2}}}dx}\]
\[\Rightarrow U=GMm{{\left[ -\frac{1}{x} \right]}_{\infty }}^{r}\]
\[\Rightarrow U=GMm\left[ -\frac{1}{r}+\frac{1}{\infty } \right]\]
\[\Rightarrow U=-\frac{GMm}{r}\]
This is the expression of potential energy for an artificial satellite.
B. Kinetic Energy
Ans: Kinetic energy is given by:
\[K.E.=\frac{1}{2}m{{v}^{2}}\]
Where m is the mass and v is the velocity.
However, for artificial satellites, velocity is given by
\[v=\sqrt{\frac{GM}{r}}\]
Where G is the gravitational constant; M is the mass of earth and r is the radius of the earth.
\[\Rightarrow K.E.=\frac{1}{2}m\left( \frac{GM}{r} \right)\]
\[\Rightarrow K.E.=K=\frac{GMm}{2r}\]
This is the expression of kinetic energy for an artificial satellite.
C. Total Energy
Ans: Total energy of satellite is given by:
\[TE=U+K\]
\[\Rightarrow TE=-\frac{GMm}{r}+\frac{GMm}{2r}\]
\[\Rightarrow TE=-\frac{GMm}{2r}\]
This is the expression of total energy for an artificial satellite.
6. Suppose There Existed a Planet That Went Around the Sun Twice as Fast as the Earth. What Would Its Orbital Size be Compared to That of the Earth?
Ans: Time taken by the Earth to complete one revolution, \[{{T}_{e}}=1\text{ year}\].
Orbital radius of the Earth in its orbit, \[{{R}_{e}}=1AU\].
Time taken by the planet to complete one revolution, \[{{T}_{p}}=\frac{1}{2}{{T}_{e}}=\frac{1}{2}year\].
Orbital radius of the planet \[={{R}_{p}}\].
From Kepler's third law of planetary motion, we can write:
\[{{\left( \frac{{{R}_{p}}}{{{R}_{e}}} \right)}^{3}}={{\left( \frac{{{T}_{p}}}{{{T}_{e}}} \right)}^{2}}\]
\[\Rightarrow \frac{{{R}_{p}}}{{{R}_{e}}}={{\left( \frac{{{T}_{p}}}{{{T}_{e}}} \right)}^{\frac{2}{3}}}\]
\[\Rightarrow \frac{{{R}_{p}}}{{{R}_{e}}}={{\left( \frac{\frac{1}{2}}{1} \right)}^{\frac{2}{3}}}\]
\[\Rightarrow \frac{{{R}_{p}}}{{{R}_{e}}}={{(0.5)}^{\frac{2}{3}}}\]
\[\Rightarrow \frac{{{R}_{p}}}{{{R}_{e}}}=0.63\]
Hence, the orbital radius of the planet will be \[0.63\] times smaller than that of the Earth.
7. Which of the Following Symptoms Is Likely to Afflict an Astronaut in Space?
A. Swollen Feet
Ans: Legs hold the whole mass in a standing place due to gravitational force.
In space, an astronaut appears weightless because of the absence of gravity. Therefore, the swollen feet of a spaceman do not affect him/her in space.
B. Swollen Face
Ans: A swollen face is usually caused because of seeming weightlessness in space.
Sense organs such as the nose, eyes, ears, and mouth establish a person's face. This symptom can affect a spacewalker in space.
C. Headache
Ans: Headaches are because of mental stress. It can influence the working of an astronaut in space.
D. Orientational Problem
Ans: Space has diverse orientations.
Therefore, orientational difficulty can affect an astronaut in space.
8. How will you 'weigh the sun', that is, estimate its mass? The mean orbital radius of the earth around the sun is \[1.5\times {{10}^{8}}km\].
Ans: Orbital radius of the Earth around the Sun, \[r=1.5\times {{10}^{11}}m\].
Time taken by the Earth to cover one revolution around the Sun,
\[T=1\text{ year}\]
\[\Rightarrow \text{T=}365.25\text{ days}\]
We get,
\[\text{T=365}\text{.25}\times \text{24}\times \text{60}\times \text{60}s\]
Universal gravitational constant,
\[G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\].
Thus, we can use the relation given below for calculating the mass of the Sun,
\[M=\frac{4{{\pi }^{2}}{{r}^{3}}}{G{{T}^{2}}}\]
\[\Rightarrow \text{M}=\frac{4\times {{(3.14)}^{2}}\times {{(1.5\times {{10}^{11}})}^{3}}}{6.67\times {{10}^{-11}}\times {{(365.25\times 24\times 60\times 60)}^{2}}}\]
\[\Rightarrow \text{M}=\frac{133.24\times {{10}^{33}}}{6.64\times {{10}^{4}}}\]
\[\Rightarrow \text{M}=2.0\times {{10}^{30}}kg\]
Hence, the mass of the Sun is \[2\times {{10}^{30}}kg\].
9. A Saturn year is \[\mathbf{29}.\mathbf{5}\] times the earth year. How far is Saturn from the sun if the earth is \[1.50\times {{10}^{8}}km\] away from the sun?
Ans: Distance of the Earth from the Sun, \[{{r}_{e}}=1.5\times 1{{0}^{8}}km=1.5\times {{10}^{11}}m\]
Time period of the Earth \[={{T}_{e}}\]
Time period of Saturn, \[{{T}_{s}}=29.5{{T}_{e}}\]
Distance of Saturn from the Sun \[={{r}_{s}}\]
From Kepler's third law of planetary motion, we have,
\[T={{\left( \frac{4{{\pi }^{2}}{{r}^{3}}}{GM} \right)}^{\frac{1}{2}}}\]
For Saturn and Sun, we can write,
\[\frac{{{r}_{s}}^{3}}{{{r}_{e}}^{3}}=\frac{{{T}_{s}}^{2}}{{{T}_{e}}^{2}}\]
\[\Rightarrow {{r}_{s}}={{r}_{e}}{{\left( \frac{{{T}_{s}}}{{{T}_{e}}} \right)}^{\frac{2}{3}}}\]
\[\Rightarrow {{r}_{s}}=1.5\times {{10}^{11}}{{\left( \frac{29.5{{T}_{e}}}{{{T}_{e}}} \right)}^{\frac{2}{3}}}\]
\[\Rightarrow {{r}_{s}}=1.5\times {{10}^{11}}{{(29.5)}^{\frac{2}{3}}}\]
\[\Rightarrow {{r}_{s}}=1.5\times {{10}^{11}}\times 9.55\]
\[\Rightarrow {{r}_{s}}=14.32\times {{10}^{11}}m\]
Hence, the distance between the Sun and Saturn is \[1.43\times {{10}^{12}}m\].
10. Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighed \[250N\] on the surface?
Ans: Weight of a body of mass \[m\] at the Earth's surface is given by,
\[W=mg=250N\]
Body of mass \[m\] is located at depth, \[d=\frac{1}{2}{{R}_{e}}\]
Where, \[{{R}_{e}}\] is the radius of the Earth.
Acceleration due to gravity at depth \[{{g}_{d}}\] is given by the relation:
\[{{g}_{d}}=\left( 1-\frac{d}{{{R}_{e}}} \right)g\]
\[\Rightarrow \left( 1-\frac{{{R}_{e}}}{2\times {{R}_{e}}} \right)g=\frac{1}{2}g\]
Weight of the body at depth \[d\],
\[W'=mg\]
\[\Rightarrow W'=m\times \frac{1}{2}g=\frac{1}{2}mg=\frac{1}{2}W\]
\[\Rightarrow W'=\frac{1}{2}\times 250=125N\]
The weight of the body half way down to the centre of the earth is $125N.$
11. A star 2.5 times the mass of the sun and collapsed to a size of \[12km\] rotates with a speed of \[1.2\] evolutions per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity? (Mass of the sun\[=2\times {{10}^{30}}kg\]).
Ans: Yes.
A body gets held to the star's surface if the inward gravitational force is larger than the outward centrifugal force generated by the star's rotation.
Gravitational force,
\[{{f}_{g}}=\frac{GMm}{{{R}^{2}}}\]
Where, M is the mass of the star, \[M=2.5\times 2\times {{10}^{30}}=5\times {{10}^{30}}kg\]
m is the mass of the body
R is the radius of the star, \[\text{R}=12km=1.2\times {{10}^{4}}m\]
\[\therefore {{f}_{g}}=\frac{6.67\times {{10}^{-11}}\times 5\times {{10}^{30}}\times m}{{{(1.2\times {{10}^{4}})}^{2}}}\]
\[{{f}_{g}}=2.31\times {{10}^{11}}mN\]
Centrifugal force, \[{{f}_{c}}=mr{{\omega }^{2}}\]
\[\omega =\text{Angular speed}=2\pi v\]
\[v=\text{Angular frequency}=1.2rev\text{ }{{s}^{-1}}\]
\[{{f}_{c}}=mR{{(2\pi v)}^{2}}\]
\[\Rightarrow {{f}_{c}}=m\times (1.2\times {{10}^{4}})\times 4\times {{(3.14)}^{2}}\times {{(1.2)}^{2}}\]
\[\Rightarrow {{f}_{c}}=1.7\times {{10}^{5}}mN\]
Since \[{{f}_{g}}>{{f}_{c}}\], the body will remain held to the surface of the star.
4 Marks Questions
1. Choose the Correct Alternative:
A. Acceleration Due to Gravity Increases/Decreases With Increasing Altitude.
Ans: Acceleration due to gravity decreases with increasing altitude.
Acceleration due to gravity at height \[h\] is given by:
\[{{g}_{h}}=\left( 1-\frac{2h}{{{R}_{e}}} \right)g\]
Where, \[{{R}_{e}}=\]Radius of the Earth
\[g=\]Acceleration due to gravity on the surface of the Earth
It is clear from the relation that acceleration due to gravity decreases with a height increment.
B. Acceleration Due to Gravity Increases/Decreases With Increasing Depth. (assume the Earth to Be a Sphere of Uniform Density).
Ans: Acceleration due to gravity decreases with increasing depth.
Acceleration due to gravity at depth \[d\] is given by:
\[{{g}_{d}}=\left( 1-\frac{d}{{{R}_{e}}} \right)g\]
It is clear from the relation that acceleration due to gravity decreases with a depth increment.
C. Acceleration Due to Gravity Is Independent of the Mass of the Earth/Mass of the Body.
Ans: Acceleration due to gravity is independent of the mass of the body.
Acceleration due to gravity of the body having mass \[m\] is given by: \[g=\frac{GM}{{{R}^{2}}}\]
Where, \[G\]= Universal gravitational constant
\[M\]= Mass of the Earth
\[R\]= Radius of the Earth
Hence, it is clear that acceleration due to gravity is not dependent on the body's mass.
D. The formula \[-GMm\left( \frac{1}{{{r}_{2}}}-\frac{1}{{{r}_{1}}} \right)\] is more/less accurate than the formula \[mg({{r}_{2}}-{{r}_{1}})\] for the difference of potential energy between two points and distance away from the centre of the earth.
Ans: Gravitational potential energy of two points at \[{{r}_{2}}\] and \[{{r}_{1}}\] distance away from the Earth centre is given by:
\[V({{r}_{1}})=-\frac{GmM}{{{r}_{1}}}\] and
\[V({{r}_{2}})=-\frac{GmM}{{{r}_{2}}}\]
\[\therefore \] Difference in potential energy,
\[V=V({{r}_{2}})-V({{r}_{1}})\]
\[\Rightarrow \text{V}=-GMm\left( \frac{1}{{{r}_{2}}}-\frac{1}{{{r}_{1}}} \right)\]
Hence, this formula is more reliable than the formula \[mg({{r}_{2}}-{{r}_{1}})\].
2. Let us assume that our galaxy consists of \[2.5\times {{10}^{11}}\] stars, each of one solar mass. How long will a star at a distance of \[50,000ly\] from the galactic centre take to complete one revolution? Take the diameter of the Milky Way to be \[{{10}^{5}}ly\].
Ans: Mass of galaxy Milky way, \[M=2.5\times {{10}^{11}}\] solar mass
Solar mass = Mass of sun\[=2.0\times {{10}^{36}}kg\]
Mass of our galaxy, \[M=2.5\times {{10}^{11}}\times 2\times {{10}^{35}}\]
\[M=5\times {{10}^{41}}kg\]
Diameter of the Milky Way, \[d={{10}^{5}}ly\]
Radius of the Milky Way, \[r=5\times {{10}^{4}}ly\]
\[1\text{ }ly=9.46\times 1{{0}^{15}}m\]
\[r=5\times {{10}^{4}}\times 9.46\times 1{{0}^{15}}\]
\[\Rightarrow \text{r}=4.73\times {{10}^{20}}m\]
Since a star rotates around the galactic centre of the Milky Way, its time period is given by:
\[T={{\left( \frac{4{{\pi }^{2}}{{r}^{3}}}{GM} \right)}^{\frac{1}{2}}}=\left( \frac{4\times {{\left( 3.14 \right)}^{2}}\times {{\left( 4.73 \right)}^{3}}\times {{10}^{60}}}{6.67\times {{10}^{-11}}\times 5\times {{10}^{41}}} \right)\]
\[\Rightarrow T={{\left( 125.27\times {{10}^{30}} \right)}^{\frac{1}{2}}}\]
\[\Rightarrow \text{T}=1.12\times {{10}^{16}}s\]
As we know,
\[1\text{ }year=365\times 24\times 60\times 60s\]
We get,
\[1s=\frac{1}{365\times 24\times 60\times 60}years\]
\[\Rightarrow 1.12\times {{10}^{16}}s=\frac{1.12\times {{10}^{16}}}{365\times 24\times 60\times 60}\]
\[\therefore 1.12\times {{10}^{16}}s=3.55\times {{10}^{8}}years\]
Thus, the star will take \[3.55\times {{10}^{8}}years\] to complete one revolution.
3. A body weighs \[63N\] on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?
Ans: Weight of the body, \[W=63N\]
Acceleration due to gravity at height \[h\] from the Earth’s surface
\[{{R}_{e}}=\]Radius of the Earth
For \[h=\frac{{{R}_{e}}}{2}\], gravity at $h$ is given by:
\[{{g}_{h}}=\frac{g}{{{\left( 1+\frac{h}{{{R}_{e}}} \right)}^{2}}}\]
\[\Rightarrow {{g}_{h}}=\frac{g}{{{\left( 1+\frac{1}{2} \right)}^{2}}}\]
\[\Rightarrow {{g}_{h}}=\frac{4}{9}g\]
Weight of a body of mass \[m\] at height \[h\] is given as:
\[W'=m{{g}_{h}}\]
\[\Rightarrow W'=m\times \frac{4}{9}g\]
\[\Rightarrow W'=\frac{4}{9}\times mg\]
\[\Rightarrow \text{W }\!\!'\!\!\text{ }=\frac{4}{9}W\]
\[\Rightarrow \text{W }\!\!'\!\!\text{ }=\frac{4}{9}\times 63\]
\[\Rightarrow W'=28N\]
Thus, the gravitational force on the body due to the earth at a height equal to half the radius of the earth is $28N$.
4. The escape speed of a projectile on the earth's surface is \[11.2km{{s}^{-1}}\]. A body is projected out with thrice this speed. What is the speed of the body far away from the earth? Ignore the presence of the sun and other planets.
Ans: Projectile’s escape velocity from the Earth, \[{{v}_{esc}}=11.2km{{s}^{-1}}\]
Projection velocity of the projectile, \[{{v}_{p}}={{3}_{{{v}_{esc}}}}\]
Mass of the projectile \[=m\]
Projectile’s velocity far away from the Earth \[={{v}_{f}}\]
Projectile’s total energy on the Earth \[=\frac{1}{2}m{{v}_{p}}^{2}-\frac{1}{2}m{{v}_{esc}}^{2}\]
The projectile's gravitational potential energy far away from the Earth is zero.
Total energy of the projectile far away from the Earth \[=\frac{1}{2}m{{v}_{f}}^{2}\]
From the law of energy conservation, we have
\[\frac{1}{2}m{{v}_{p}}^{2}-\frac{1}{2}m{{v}_{esc}}^{2}=\frac{1}{2}m{{v}_{f}}^{2}\]
We get,
\[{{v}_{f}}=\sqrt{{{v}_{p}}^{2}-{{v}_{esc}}^{2}}\]
\[\Rightarrow {{v}_{f}}=\sqrt{{{(3{{v}_{esc}})}^{2}}-{{({{v}_{esc}})}^{2}}}\]
\[\Rightarrow {{v}_{f}}=\sqrt{8}{{v}_{esc}}\]
\[\Rightarrow {{v}_{f}}=\sqrt{8}\times 11.2\]
\[\Rightarrow {{v}_{f}}=31.68km{{s}^{-1}}\]
Thus, the speed of the body far away from the earth is \[31.68km{{s}^{-1}}\].
5. Choose the Correct Answer from Among the Given Ones:
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12).
a,
b,
c,
O
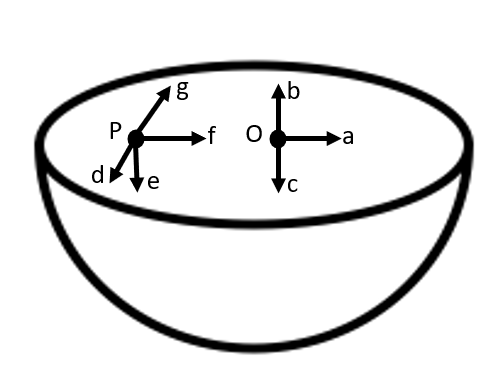
Ans: Option (iii) is correct.
Gravitational potential (\[V\]) is fixed at all points in a spherical shell. Hence, the potential gravitational gradient \[\left( \frac{dV}{dr} \right)\] is zero everywhere inside the spherical surface.
The potential gravitational gradient is equivalent to the negative of gravitational intensity. Hence, intensity is also zero at all locations inside the spherical shell. This shows that gravitational forces operating at a point in a spherical shell are symmetric.
If the top half of a spherical shell is cut out, then the net gravitational force working on a particle located at centre O will be downward.
Since gravitational intensity is described as the gravitational force per unit mass at that location, it will also act downward. Thus, the gravitational intensity at the centre of the given hemispherical shell has the direction indicated by the arrow \[c\].
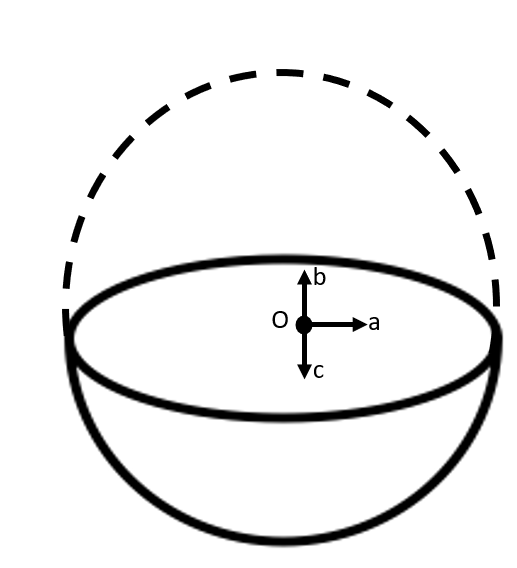
6. Choose the Correct Answer from Among the Given Ones:
For the problem 8.10, the direction of the gravitational intensity at an arbitrary point \[P\] is indicated by the arrow
d,
e,
f,
g.
Ans: Option (ii) is correct.
Gravitational potential (\[V\]) is fixed at all points in a spherical shell. Hence, the potential gravitational gradient \[\left( \frac{dV}{dr} \right)\] is zero everywhere inside the spherical surface.
The potential gravitational gradient is equivalent to the negative of gravitational intensity. Hence, intensity is also zero at all locations inside the spherical shell. This shows that gravitational forces operating at a point in a spherical shell are symmetric.
If the top half of a spherical shell is cut out, then the net gravitational force working on a particle located at centre P will be downward.
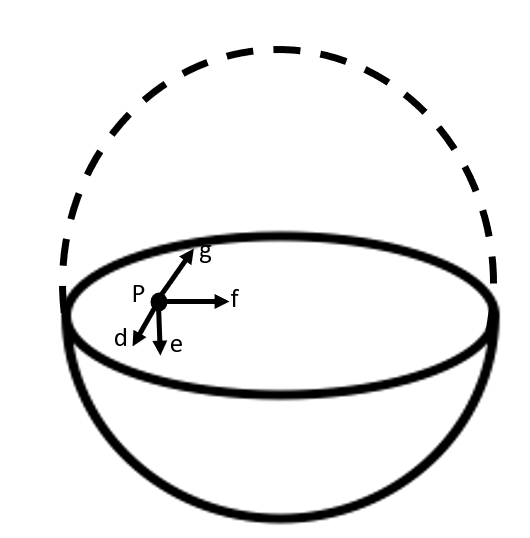
Since gravitational intensity is described as the gravitational force per unit mass at that location, it will also act downward.
Thus, the gravitational intensity at the arbitrary point P of the given hemispherical shell has the direction indicated by the arrow \[e\].
7. A satellite orbits the earth at a height of \[400km\] above the surface. How much energy must be expended to rocket the satellite out of the earth's gravitational influence?
Mass of the satellite\[=200kg\];
mass of the earth\[=6.0\times {{10}^{24}}kg\];
radius of the earth\[=6.4\times {{10}^{6}}\]; \[G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\].
Ans: Given that,
Mass of the Earth, \[{{M}_{e}}=6.0\times {{10}^{24}}kg\]
Mass of the satellite, \[m=200kg\]
Radius of the Earth, \[{{R}_{e}}=6.4\times {{10}^{6}}m\]
Universal gravitational constant, \[G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\]
Height of the satellite, \[h=400km=4\times {{10}^{5}}m=0.4\times {{10}^{6}}m\]
Total energy of the satellite at height $h$,
\[TE=\frac{1}{2}m{{v}^{2}}+\left( \frac{-G{{M}_{e}}m}{{{R}_{e}}+h} \right)\]
Orbital velocity of the satellite, \[v=\sqrt{\frac{G{{M}_{e}}}{{{R}_{e}}+h}}\]
Total energy at height $h$, \[TE=\frac{1}{2}m\left( \frac{G{{M}_{e}}}{{{R}_{e}}+h} \right)-\frac{G{{M}_{e}}m}{{{R}_{e}}+h}=-\frac{1}{2}\left( \frac{G{{M}_{e}}m}{{{R}_{e}}+h} \right)\]
The negative sign explains that the satellite is attached to the Earth. This is called the bound energy of the satellite.
The energy needed to send the satellite out of its orbit is equal to the negative of Bound energy.
Bound energy is, \[BE=\frac{1}{2}\left( \frac{G{{M}_{e}}m}{{{R}_{e}}+h} \right)\]
Where, ${{M}_{e}}$ is the mass of the Earth.
${{R}_{e}}$ is the radius of the Earth.
h is the height.
m is the mass of the satellite.
\[\Rightarrow BE=\frac{1}{2}\times \frac{6.67\times {{10}^{-11}}\times 6.0\times {{10}^{24}}\times 200}{\left( 6.4\times {{10}^{6}}+0.4\times {{10}^{6}} \right)}\]
\[\Rightarrow BE=\frac{1}{2}\times \frac{6.67\times 6\times 2\times 10}{6.4\times {{10}^{6}}}\]
\[\Rightarrow BE=5.9\times {{10}^{9}}J\]
Clearly, \[5.9\times {{10}^{9}}J\] energy must be expended to rocket the satellite out of the earth's gravitational influence.
5 Marks Questions
1. Define Gravitational Potential Energy. Hence Deduce an Expression for the Gravitational Potential Energy of a Body Placed at a Point Near the Surface of Earth.
Ans: The gravitational potential energy is described as the work done in taking a body from infinity to that point, where it is being measured.
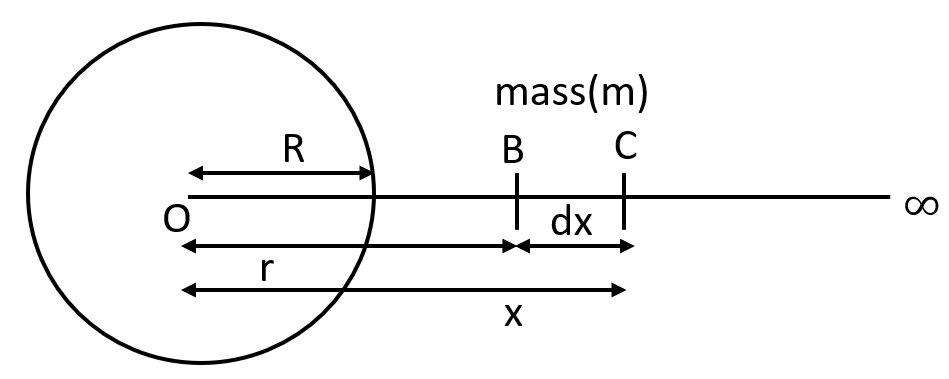
For a body having mass (\[m\]) lying at a distance \[x\] from the mass of earth (\[M\]):
\[F=\frac{GMm}{{{x}^{2}}}\]
If the body is displaced through a distance \[dx\],then
\[dw=Fdx=\frac{GMm}{{{x}^{2}}}dx\]
Total work done,
\[w=\int\limits_{\infty }^{r}{\frac{GMm}{{{x}^{2}}}dx}\]
\[\Rightarrow w=GMm\int\limits_{\infty }^{r}{\frac{1}{{{x}^{2}}}dx}\]
\[\Rightarrow w=GMm\left[ \frac{-1}{x} \right]_{\infty }^{r}\]
\[\Rightarrow w=-GMm\left[ \frac{1}{r}-\frac{1}{\infty } \right]\]
\[\Rightarrow w=\frac{-GMm}{r}\]
This work done is equal to gravitational potential energy.
\[w={{U}_{g}}=\frac{-GMm}{r}\]
This is an expression for the gravitational potential energy of a body placed at a point near the surface of earth.
2. ${{I}_{O}}$, one of the satellites of Jupiter, has an orbital period of \[1.769\text{ }days\] and the radius of the orbit is \[4.22\times {{10}^{8}}m\]. Show that the mass of Jupiter is about one-thousandth that of the sun.
Ans: Given that,
Orbital period of \[{{I}_{O}}={{T}_{{{I}_{O}}}}=1.769days=1.769\times 24\times 60\times 60s\]
Orbital radius of \[{{I}_{O}}={{R}_{{{I}_{O}}}}=4.22\times {{10}^{8}}m\]
Satellite \[{{I}_{O}}\] is revolving around Jupiter.
Mass of Jupiter is given by:
\[{{M}_{J}}=\frac{4{{\pi }^{2}}R_{{{I}_{o}}}^{3}}{GT_{{{I}_{o}}}^{2}}\]......(i)
Where, \[{{M}_{J}}\]= Mass of Jupiter
\[G\]is the Universal gravitational constant
Orbital period of the Earth,
\[{{T}_{e}}=365.25days=365.25\times 25\times 60\times 60s\]
Orbital radius of the Earth,
\[{{R}_{e}}=1AU=1.496\times {{10}^{11}}m\]
Mass of the sun is given as:
\[{{M}_{s}}=\frac{4{{\pi }^{2}}R_{e}^{3}}{GT_{e}^{2}}\]......(ii)
\[\Rightarrow \frac{{{M}_{S}}}{{{M}_{J}}}=\frac{4{{\pi }^{2}}R_{e}^{3}}{GT_{e}^{2}}\times \frac{GT_{Io}^{2}}{4{{\pi }^{2}}R_{Io}^{3}}=\frac{R_{e}^{3}}{R_{Io}^{3}}\times \frac{T_{Io}^{2}}{T_{e}^{2}}\]
\[\Rightarrow \frac{{{M}_{S}}}{{{M}_{J}}}={{\left( \frac{1.769\times 24\times 60\times 60}{365.25\times 24\times 60\times 60} \right)}^{2}}\times {{\left( \frac{1.496\times {{10}^{11}}}{4.22\times {{10}^{8}}} \right)}^{3}}\]
\[\Rightarrow \frac{{{M}_{S}}}{{{M}_{J}}}=1045.04\]
\[\therefore \frac{{{M}_{s}}}{{{M}_{J}}}\sim 1000\]
We get,
\[{{M}_{s}}\sim 1000\times {{M}_{J}}\]
Hence, it can be concluded that the mass of Jupiter is about one-thousandth that of the Sun.
3. A rocket is fired from the earth towards the sun. At what distance from the earth's centre is the gravitational force on the rocket zero?
Mass of the sun\[=2\times {{10}^{30}}kg\], mass of the earth\[=6\times {{10}^{24}}kg\]. Neglect the effect of other planets etc. (orbital radius\[=1.5\times {{10}^{11}}m\]).
Ans: Mass of the Sun, \[{{M}_{s}}=2\times {{10}^{30}}kg\]
Mass of the Earth, \[{{M}_{e}}=6\times {{10}^{24}}kg\]
Orbital radius, \[r=1.5\times {{10}^{11}}m\]
Mass of the rocket=\[m\]
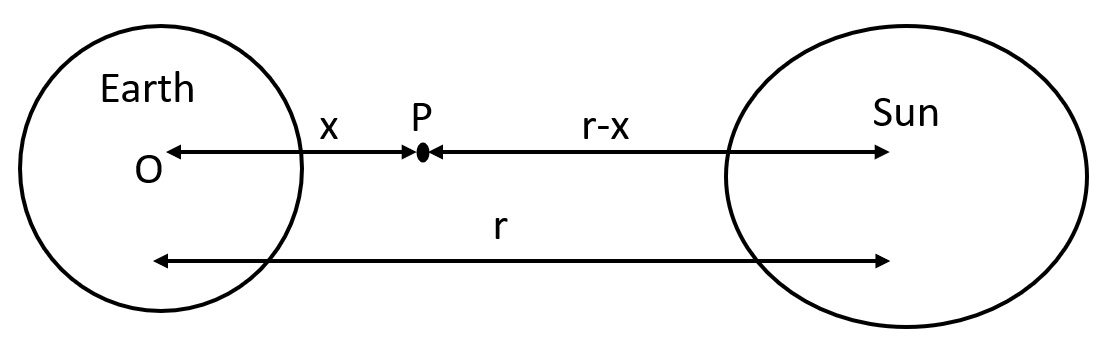
Let \[x\] be the distance from the Earth centre where the gravitational force working on the satellite \[P\] becomes zero.
From Newton's law of gravitation, we can equalize gravitational forces acting on satellites \[P\] under the effect of the Sun and the Earth as:
\[\frac{Gm{{M}_{s}}}{{{\left( r-x \right)}^{2}}}=Gm\frac{{{M}_{e}}}{{{x}^{2}}}\]
We get,
\[{{\left( \frac{r-x}{x} \right)}^{2}}=\frac{{{M}_{s}}}{{{M}_{e}}}\]
\[\Rightarrow \frac{r-x}{x}={{\left( \frac{2\times 1{{0}^{30}}}{60\times {{10}^{24}}} \right)}^{\frac{1}{2}}}=577.35\]
\[\Rightarrow 1.5\times {{10}^{11}}-x=577.35x\]
\[\Rightarrow 578.35x=1.5\times {{10}^{11}}\]
\[\Rightarrow x=\frac{1.5\times {{10}^{11}}}{578.35}=2.59\times {{10}^{8}}m\]
Therefore, \[2.59\times {{10}^{8}}m\] is the distance from the earth's centre at which the gravitational force on the rocket is zero.
4. A rocket is fired vertically with a speed of \[5km{{s}^{-1}}\] from the earth's surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth\[=6.0\times {{10}^{24}}kg\]; mean radius of the earth\[=6.4\times {{10}^{6}}m;G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\].
Ans: Distance from the centre of the Earth \[=8\times {{10}^{6}}m\]
Velocity of the rocket, \[v=5km{{s}^{-1}}=5\times {{10}^{3}}m{{s}^{-1}}\]
Mass of the Earth, \[{{M}_{e}}=6.0\times {{10}^{24}}kg\]
Radius of the Earth, \[{{R}_{e}}=6.4\times {{10}^{6}}m\]
Height reached by rocket mass $m$, is \[h\].
At the surface of the Earth,
Total energy of the rocket = Kinetic energy + Potential energy
\[=\frac{1}{2}m{{v}^{2}}+\left( \frac{-G{{M}_{e}}m}{{{R}_{e}}} \right)\]
At highest point $h,$ \[v=0\]
And, Potential energy \[=-\frac{G{{M}_{e}}m}{{{R}_{e}}+h}\]
Total energy of the rocket\[=0+\left( \frac{G{{M}_{e}}m}{{{R}_{e}}+h} \right)=-\frac{G{{M}_{e}}m}{{{R}_{e}}+h}\]
From the law of energy conservation, we have
Total energy of the rocket at the Earth's surface = Total energy of rocket at height \[h\].
We have,
\[\frac{1}{2}m{{v}^{2}}+\left( -\frac{G{{M}_{e}}m}{{{R}_{e}}} \right)=-\frac{G{{M}_{e}}m}{{{R}_{e}}+h}\]
\[\Rightarrow \frac{1}{2}{{v}^{2}}=G{{M}_{e}}\left( \frac{1}{{{R}_{e}}}-\frac{1}{{{R}_{e}}+h} \right)\]
\[\Rightarrow \frac{1}{2}{{v}^{2}}=G{{M}_{e}}\left( \frac{{{R}_{e}}+h-{{R}_{e}}}{{{R}_{e}}({{R}_{e}}+h)} \right)\]
\[\Rightarrow \frac{1}{2}{{v}^{2}}=\frac{G{{M}_{e}}h}{{{R}_{e}}({{R}_{e}}+h)}\times \frac{{{R}_{e}}}{{{R}_{e}}}\]
\[\Rightarrow \frac{1}{2}{{v}^{2}}=\frac{g{{R}_{e}}h}{{{R}_{e}}+h}\]
Where, \[g=\frac{GM}{R_{e}^{2}}=9.8m{{s}^{-2}}\] , is the acceleration due to gravity on the Earth’s surface.
Clearly,
\[{{v}^{2}}({{R}_{e}}+h)=2g{{R}_{e}}h\]
\[\Rightarrow {{v}^{2}}{{R}_{e}}=h(2g{{R}_{e}}-{{v}^{2}})\]
\[\Rightarrow h=\frac{{{R}_{e}}{{v}^{2}}}{2g{{R}_{e}}-{{v}^{2}}}\]
\[\Rightarrow \text{h}=\frac{6.4\times 25\times {{10}^{12}}}{100.44\times 1{{0}^{6}}}\]
\[\Rightarrow \text{h}=1.6\times {{10}^{6}}m\]
Height achieved by the rocket with respect to the centre of the Earth, $H$ is given by: \[H={{R}_{e}}+h\]
\[\Rightarrow H=6.4\times {{10}^{6}}+1.6\times {{10}^{6}}\]
We get,
\[H=8.0\times {{10}^{6}}m\]
The distance from the earth is \[8.0\times {{10}^{6}}m\] where the rocket goes before returning to the earth.
5. Two stars each of one solar mass (\[=2\times {{10}^{30}}kg\]) are approaching each other for a head on collision. When they are a distance \[{{10}^{9}}km\], their speeds are negligible. What is the speed with which they collide? The radius of each star is \[{{10}^{4}}km\]. Assume the stars to remain undistorted until they collide. (Use the known value of \[G\]).
Ans: Mass of each star, \[M=2\times {{10}^{30}}kg\]
Radius of each star, \[R={{10}^{4}}km={{10}^{7}}m\]
Distance between the stars, \[r={{10}^{9}}km={{10}^{12}}m\]
For negligible speeds, \[v=0\]
Total energy of two stars separated at distance \[r\] is given by
\[TE=\frac{-GMM}{r}+\frac{1}{2}m{{v}^{2}}\]
\[\Rightarrow TE=\frac{GMM}{r}+0.\]……(i)
Now, consider the case when the stars are about to collide:
Velocity of the stars \[=v\]
Distance between the centres of the stars \[=2R\]
Total kinetic energy of both stars \[=\frac{1}{2}M{{v}^{2}}+\frac{1}{2}M{{v}^{2}}=M{{v}^{2}}\]
Total potential energy of both stars\[=\frac{-GMM}{2R}\]
Total energy of the two stars \[=M{{v}^{2}}-\frac{GMM}{2R}\]........(ii)
Using the law of conservation of energy, we can write:
\[M{{v}^{2}}-\frac{GMM}{2R}=\frac{-GMM}{R}\]
\[\Rightarrow {{v}^{2}}=\frac{-GM}{r}+\frac{GM}{2r}=GM\left( -\frac{1}{r}+\frac{1}{2R} \right)\]
\[\Rightarrow {{v}^{2}}=6.67\times 1{{0}^{-10}}\times 2\times {{10}^{30}}\left[ -\frac{1}{{{10}^{12}}}+\frac{1}{2\times {{10}^{7}}} \right]\]
\[\Rightarrow {{v}^{2}}=13.34\times {{10}^{19}}\left[ -{{10}^{-12}}+5\times {{10}^{-8}} \right]\]
\[\Rightarrow {{v}^{2}}\sim 13.34\times {{10}^{19}}\times 5\times {{10}^{-8}}\]
\[\Rightarrow {{v}^{2}}\sim 6.67\times {{10}^{12}}\]
\[\Rightarrow v=\sqrt{6.67\times {{10}^{12}}}\]
\[\Rightarrow v=2.58\times {{10}^{6}}m/s\]
The speed with which the two stars collide is \[2.58\times {{10}^{6}}m/s\].
6. Two heavy spheres each of mass \[100kg\] and radius \[0.10m\] are placed \[1.0m\] apart on a horizontal table. What is the gravitational force and potential at the midpoint of the line joining the centres of the spheres? Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?
Ans: The situation is represented in the given figure:
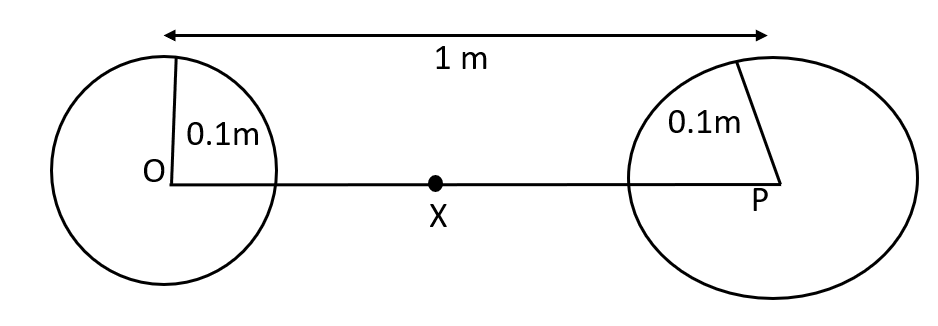
Mass of each sphere, \[M=100kg\]
Separation between the spheres, \[r=1m\]
\[X\] is the midpoint between the spheres. Gravitational force at point \[X\] will be zero. This is because the gravitational force applied by each sphere will act in opposite directions.
Gravitational potential at point \[X\]\[=\frac{-GM}{\left( \frac{r}{2} \right)}-\frac{GM}{\left( \frac{r}{2} \right)}\]
\[\Rightarrow PE=-4\frac{GM}{r}\]
\[\Rightarrow PE=\frac{4\times 6.67\times {{10}^{-11}}\times 100}{r}\]
\[\Rightarrow PE=-2.67\times {{10}^{-8}}J/kg\]
Any object placed at point \[X\] will be in equilibrium state, but the equilibrium is unstable. This is because any change in the position of the object will vary the effective force in that direction.
7. A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system?
Mass of the spaceship\[=1000kg\]; mass of the Sun\[=2\times {{10}^{30}}kg\];
mass of mars\[=6.4\times {{10}^{23}}kg\]; radius of mars\[=3395km\];
radius of the orbit of mars\[=2.28\times {{10}^{8}}kg;G=6.67\times {{10}^{-11}}{{m}^{2}}k{{g}^{-2}}\].
Ans: Mass of the spaceship, \[{{m}_{s}}=1000kg\]
Mass of the Sun, \[M=2\times 1{{0}^{30}}kg\]
Mass of Mars, \[{{M}_{m}}=6.4\times {{10}^{23}}kg\]
Orbital radius of Mars, \[R=2.28\times {{10}^{8}}kg=2.28\times {{10}^{11}}m\]
Radius of Mars, \[r=3395km=3.395\times {{10}^{6}}m\]
Universal gravitational constant, \[G=6.67\times {{10}^{-11}}{{m}^{2}}k{{g}^{-2}}\]
Potential energy of the spaceship due to the gravitational attraction of the Sun\[=\frac{-GM{{m}_{s}}}{R}\]
Potential energy of the spaceship due to the gravitational attraction of Mars\[=\frac{-G{{M}_{m}}{{m}_{s}}}{r}\]
Since the spaceship is stationed on Mars, its velocity and hence, its kinetic energy will be zero.
Total energy of the spaceship \[=\frac{-GM{{m}_{s}}}{R}-\frac{G{{M}_{m}}{{m}_{s}}}{r}\]
\[TE=-G{{m}_{s}}\left( \frac{M}{R}+\frac{{{M}_{m}}}{r} \right)\]
The negative sign indicates that the system is in a bound state.
Energy required for launching the spaceship out of the solar system = – (Total energy of the spaceship)
We have,
\[E=G{{m}_{s}}\left( \frac{M}{R}+\frac{{{m}_{m}}}{r} \right)\]
\[\Rightarrow E=6.67\times 1{{0}^{-11}}\times {{10}^{3}}\times \left( \frac{2\times {{10}^{30}}}{2.28\times {{10}^{11}}}+\frac{6.4\times {{10}^{23}}}{3.395\times {{10}^{5}}} \right)\]
\[\Rightarrow E=6.67\times {{10}^{-8}}\left( 87.72\times {{10}^{17}}+1.88\times {{10}^{17}} \right)\]
\[\Rightarrow E=6.67\times {{10}^{-8}}\times 1.88\times {{10}^{17}}\]
\[\Rightarrow E=596.97\times {{10}^{9}}\]
\[\Rightarrow E=6\times {{10}^{11}}J\]
The required energy for the spaceship to launch it out of the solar system is \[6\times {{10}^{11}}J\].
8. A rocket is fired 'vertically' from the surface of mars with a speed of \[2km/s\]. If \[20%\] of its initial energy is lost due to Martian atmospheric resistance, how far will the rocket go from the surface of mars before returning to it? Mass of mars\[=6.4\times {{10}^{23}}kg\]; radius of mars\[=3395km\];\[G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\].
Ans: Initial velocity of the rocket, \[v=2km/s=2\times {{10}^{3}}m/s\]
Mass of Mars, \[M=6.4\times {{10}^{23}}kg\]
Radius of Mars, \[R=3395km=3.395\times {{10}^{6}}m\]
Universal gravitational constant, \[G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\]
Mass of the rocket\[=m\]
Initial kinetic energy of the rocket \[=\frac{1}{2}m{{v}^{2}}\]
Initial potential energy of the rocket \[=\frac{-GMm}{R}\]
Total initial energy \[=\frac{1}{2}m{{v}^{2}}-\frac{GMm}{R}\]
If \[20%\] of initial kinetic energy is lost due to Martian atmospheric resistance, then it shows only \[80%\] of its kinetic energy helps in reaching a height.
Total initial energy available, \[TE=\frac{80}{100}\times \frac{1}{2}m{{v}^{2}}-\frac{GMm}{R}\]
\[TE=0.4m{{v}^{2}}-\frac{GMm}{R}\]
Maximum height reached by the rocket\[=h\]
At this height, the velocity and hence, the kinetic energy of the rocket will become zero.
Total energy of the rocket at height $h,$ \[=-\frac{GMm}{\left( R+h \right)}\]
Applying the law of energy conservation for the rocket, we can write:
\[0.4m{{v}^{2}}-\frac{GMm}{R}=\frac{-GMm}{\left( R+h \right)}\]
\[\Rightarrow 0.4{{v}^{2}}=\frac{GM}{R}-\frac{GM}{R+h}\]
\[\Rightarrow 0.4{{v}^{2}}=GM\left( \frac{1}{R}-\frac{1}{R+h} \right)\]
\[\Rightarrow 0.4{{v}^{2}}=GM\left( \frac{R+h-R}{R\left( R+h \right)} \right)\]
After solving further, we get
\[0.4{{v}^{2}}=\frac{GMh}{R\left( R+h \right)}\]
\[\Rightarrow \frac{R+h}{h}=\frac{GM}{0.4{{v}^{2}}R}\]
\[\Rightarrow \frac{R}{h}+1=\frac{GM}{0.4{{v}^{2}}R}\]
\[\Rightarrow \frac{R}{h}=\frac{GM}{0.4{{v}^{2}}R}-1\]
\[\Rightarrow h=\frac{R}{\frac{GM}{0.4{{v}^{2}}R}-1}\]
\[\Rightarrow h=\frac{0.4{{R}^{2}}{{v}^{2}}}{GM-0.4{{v}^{2}}R}\]
Putting all the values, we get,
\[h=\frac{0.4\times {{\left( 3.395\times {{10}^{6}} \right)}^{2}}\times {{\left( 2\times {{10}^{3}} \right)}^{2}}}{6.67\times 1{{0}^{-11}}\times 6.4\times {{10}^{23}}-0.4\times {{\left( 2\times {{10}^{3}} \right)}^{2}}\times \left( 3.395\times {{10}^{6}} \right)}\]
\[\Rightarrow h=\frac{18.442\times {{10}^{18}}}{42.688\times {{10}^{12}}-53432\times {{10}^{12}}}\]
\[\Rightarrow h=\frac{18.442}{37.256}\times {{10}^{6}}\]
\[\Rightarrow h=495\times {{10}^{3}}m\]
\[\Rightarrow h=495km\]
So, the height attained by the rocket from the surface will be $495km$.
Class 11 Physics Chapter 7 Important Questions PDF
We at this platform provide you with the best possible ways to crack the exam with a good score. Here, we will dig deeper into what necessary facts and figures we need to know. Also, we will discuss Class 11 Physics Chapter 7 Important Questions for your upcoming exams included in the PDF.
Importance of Class 11 Physics Chapter 7 Gravitation
Class 11 Physics Chapter 7 is one of the interesting chapters that talks all about how our universe works. We all know that Chapter 7 Gravitation lays a pioneer position in the history of college entrance exams like IIT, NEET, TS EAMCET, UKSEE, and many more state entrance exams. You must note that one question from this chapter was also asked in IIT JEE in the previous year. A 2% weightage is expected for Class 11 Physics Chapter 7 Gravitation in NEET 2024.
Gravitation Class 11 Important Questions
Now, let’s go through a few Important Questions of Gravitation Class 11:
Question 1: The earth approximately is spherical. If its interior contains a matter which is not of the same density on each side, then on the surface of the earth, the acceleration due to gravity will be?
Options:
Directed towards the centre of the earth but varies everywhere.
Having the same value but not directed towards the centre.
Having the same magnitude everywhere and also directed towards the centre.
Can never be zero at any point.
Answer: Option (d): ‘g’ cannot be zero at any point.
Question 2: Three particles of masses 2M, m, and M are placed at points A, B, and C, respectively with AB = (½) (BC).
A body of mass ‘m’ is very small than M and initially, at time t = 0, they all are at rest (see Fig. 8.1). At subsequent times before any collision takes place, what will happen?
Options:
Mass ‘m’ move towards mass ‘M’.
Mass ‘m’ remains at rest.
Mass ‘m’ moves towards ‘2M’.
Mass ‘m’ makes oscillatory movements.
Answer: Option (c): Mass ‘m’ moves towards mass ‘2M’.
Class 11 Physics Chapter 7 Important Topics
Important subtopics to cover in Class Physics Chapter 7 Gravitation are as follows:
Escape Velocity.
Three laws of Kepler of planetary motion.
Universal Law of Gravitation.
Variation of the value of Acceleration due to gravity ‘g’:
With respect to depth
With respect to the altitude
Gravitational Potential and Gravitational Potential Energy.
Orbital velocity.
Geo-stationary satellite.
Gravitational field intensity.
Mass and mean density of Earth.
Principle of superposition of Gravitation.
What You Will Get to Know on Vedantu?
On this page, you will get to know the latest set of questions that are prepared by our subject-matter experts after doing thorough research on the history of varying exams.
Going through our website, you will have access to PYQPs, a fresh set of questions, sample papers, and much more study materials that will only guide you with a complete understanding of how to score high in the board exams but also help you to prepare well and excel in competitive exams.
Conclusion
The compilation of Important Questions for CBSE Class 11 Physics Chapter 7 - "Gravitation" is an invaluable resource for students. These questions are strategically selected to cover essential concepts and principles related to gravitation, offering a targeted approach to exam preparation. They assist students in identifying key topics for revision and provide an opportunity for self-assessment. By aligning with the examination pattern and level of difficulty, these important questions empower students to build confidence and competence in the subject. Ultimately, they serve as a critical tool for Class 11 Physics students, enabling them to excel in their studies and perform effectively in their exams, while also fostering a deeper understanding of the universal force of gravity.
Important Related Links for CBSE Class 11
