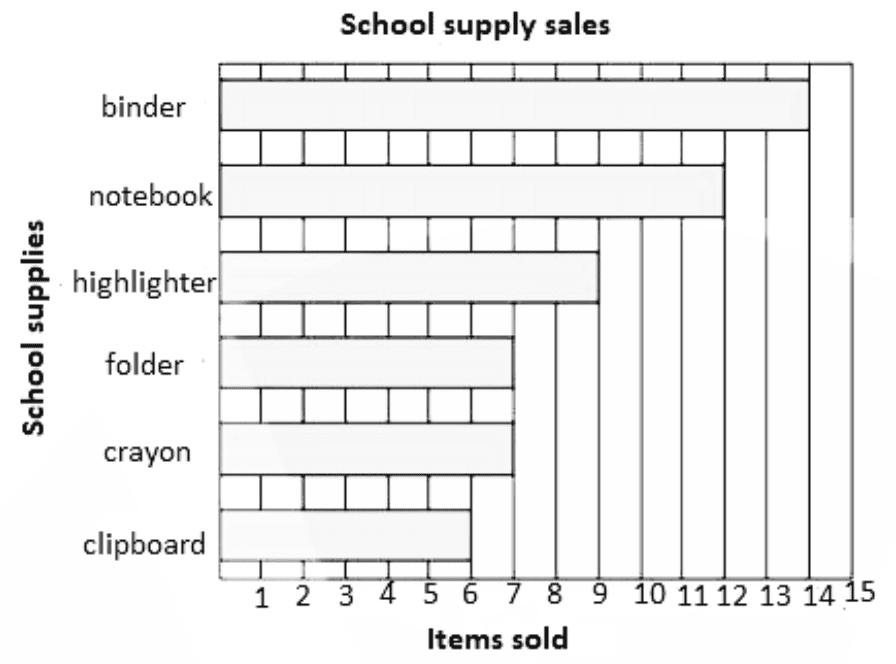
Data Handling Class 8 Important Questions: CBSE Maths Chapter 4

Very Short Answer Type Questions (1 Mark)

1. Collections of Observations are called _______

Ans: Data

2. Difference between highest and lowest values of Observations in a data is called 

_______ of the data.

Ans: Range

3. The number of times a particular observation occurs in a given data is called 

________

 Ans: Frequency

4. Define class size.

Ans: The difference between the upper limit and lower limit of a class interval is called 

class size.

5. ________ is a pictorial representation of numerical data in the form of rectangle 

(bars) of equal width and varying lengths.

Ans:Bar Graph

6. An operation which produce some well defined outcomes is called an _______ 

Ans: Random Experiment

7. Each outcome of an experiment is called ________

Ans: Trial

Short Answer Type Questions (2 Marks)

1. Define a random experiment and a trial

Ans: An experiment in which all possible outcomes are already known and the exact outcome cannot be predicted in advance is called a random experiment.

Trial means performing a random experiment.

2. Define probability of occurrence of an event.

Ans: Let \[{\text{E}}\] be an event, then the probability of occurrence of \[{\text{E}}\] is defined as,

${\text{P(E)}} = \dfrac{{{\text{ Number of outcomes favourable to E}}}}{{{\text{ Total number of possible outcomes }}}}$

3. A coin is tossed. What is the probability of getting a tail?

Ans: When a coin is tossed the possible outputs are \[{\text{H, T}}\].

The probability of getting a tail is $\dfrac{1}{2}$.

4. In a deck of \[52\] cards, what is the probability of getting

(a) Black cards

Ans:Total black cards $ = 26$

The probability of getting Black cards is,

${\text{P(E)}} = \dfrac{{26}}{{52}}$

(b) Red cards

Ans: Total Red cards $ = 26$

The probability of getting Red cards is,

${\text{P(E)}} = \dfrac{{26}}{{52}}$

(c) Face cards

Ans: Total Face cards $ = 12$

The probability of getting Face cards is,

${\text{P(E)}} = \dfrac{{12}}{{52}}$

5. When a die is thrown what is the probability of getting prime?

Ans: The possible outcomes when a die is thrown are $1,2,3,4,5,6 = 6$ outcomes the prime numbers are \[2,3,5\].

The possibility of getting prime numbers ${\text{P(E)}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Short Answer Type Questions (3 Mark)

1. Define class intervals, upper limit and lower limit with examples.

Ans: When the number of observations is large, the data is usually organized into graphs called class interval.

The lower value of a class interval is called the lower limit and upper value of class interval is called the upper limit.

Example: \[40{\text{ }} - {\text{ }}45\]class interval

Lower limit $ - \,\,40$

Upper limit $ - \,\,45$

2. Explain the components of a well shuffled deck of \[52\] cards.

Ans: A deck of playing cards has in all \[52\] cards,

(i) It has \[13\] cards, each \[4\] suits namely spades, clubs, hearts and diamonds.

(ii) Cards of spades and cubes are black cards.

(iii) Cards of hearts and diamonds are red cards.

(iv) Kings, Queen and Jacks are known as face cards. Thus, these are in all \[12\] face cards.

3. Out of 45 students in a class 30 are boys and 15 are girls. If chosen randomly what 

is the probability that the student is a

(a) boy

Ans: Total number of students $ = 45$

The probability of the student is boy $ = \dfrac{{30}}{{45}} = \dfrac{2}{3}$.

(b) girl

Ans:Total number of students $ = 45$

The probability of the student is girl $ = \dfrac{{15}}{{45}} = \dfrac{1}{3}$.

4. A die is thrown once. What is the probability of

(a) number being less than \[1\]

Ans:Total possible outcomes $ = 1,2,3,4,5,6$

Number being less than $1 =  = \dfrac{0}{6} = 0$.

(b) Number being greater than \[{\mathbf{3}}\]

Ans:Total possible outcomes $ = 1,2,3,4,5,6$

Number being greater than $3 = \dfrac{3}{6} = \dfrac{1}{2}$.

Long Answer Type Questions (4 Marks)

1. The below is the data of height of different players recorded. Arrange the data in ascending order and state the frequency of each observation and prepare frequency 

table.

$120\;{\text{cm}},100\;{\text{cm}},110\;{\text{cm}},109\;{\text{cm}},100\;{\text{cm}},108\;{\text{cm}},100\;{\text{cm}},110\;{\text{cm}},109\;{\text{cm}},120\;{\text{cm}},108\;{\text{cm}}$,

$107\;{\text{cm}},102\;{\text{cm}},101\;{\text{cm}},150\;{\text{cm}},110\;{\text{cm}},108\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}}$.

Ans: Ascending order: $100\;{\text{cm}},100\;{\text{cm}},100\;{\text{cm}},101\;{\text{cm}},102\;{\text{cm}},107\;{\text{cm}},108\;{\text{cm}},108\;{\text{cm}},108\;{\text{cm}}$,$109\;{\text{cm}},110\;{\text{cm}},110\;{\text{cm}},110\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},120\;{\text{cm}},150\;{\text{cm}}$

2. When three coins are tossed simultaneously, what are all the possible outcomes? 

Ans: When three coins are tossed simultaneously the possible outcomes are,

\[{\text{HHH, HHT, HTH, THH, TTT, TTH, THT, HTT}}\]

What is the probability of getting

(a) all tails

Ans: The probability of getting all tails $ = \dfrac{1}{8}$.

(b) at least one head.

Ans: The probability of getting at least one head $ = \dfrac{7}{8}$.

Long Answer Type Questions (5 Marks)

1. Given below are the $\% $ of attendance obtained by \[20\] students:

\[87,58,80,36,90,92,98,100,84,85,23,52,60,74,89,91,93,87,24,100.\]

Ans: Ascending order $ - 23,24,36,52,58,60,74,80,84,85,87,87,89,90,91,92,93,100,100$

Arrange the data in ascending order and find

(a) Lowest attendance

Ans: Lowest attendance is $23\% $.

(b) Highest attendance

Ans: Highest attendance is $100\% $.

(c) Range

Ans: Range $ = 100 - 23 = 77\% $

2. Draw a Bar Graph for the data given below:

Scale: $x$ Axis $ = 1\;{\text{cm}}\,{\text{ = }}\,1$ item, $y$ axis $ = 1\;{\text{cm}} = 1$ item

Ans:

3. The bar graph given below shows the sales of books (in thousand number) from six branches of a publishing company during two consecutive years \[2000{\text{ and }}2001.\]

a) What is the ratio of the total sales of branch ${\text{B}}2$ for both years to the total sales of  branch \[{\text{B4}}\] for both years?

Ans:Required ratio $ = \dfrac{{(75 + 65)}}{{(85 + 95)}} = \dfrac{{140}}{{180}} = \dfrac{7}{9}$.

b) Total sales of branch ${\text{B}}6$ for both the years is what percent of the total sales of branches ${\text{B}}3$ for both the years?

Ans: Required percentage $ = \left[ {\dfrac{{(70 + 80)}}{{(95 + 110)}} \times 100} \right]\% $

$ = \left[ {\dfrac{{150}}{{205}} \times 100} \right]\% $

$ = 73.17\% .$

c) What percent of the average sales of branches ${\text{B}}1,\;\,{\text{B}}2$ and ${\text{B}}3$ in 2001 is the average 

sales of branches \[{\text{B1, B3}}\]and \[{\text{B6}}\]in \[2000?\]

Ans: Average sales (in thousand number) of branches \[{\text{B1, B3 and B6 in 2000}}\]$ = \dfrac{1}{3} \times (80 + 95 + 70) = \left( {\dfrac{{245}}{3}} \right).$

Average sales (in thousand number) of branches \[{\text{B1, B2 and B3 in 2001}}\]

$ = \dfrac{1}{3}{\text{x}}(105 + 65 + 110) = \left( {\dfrac{{280}}{3}} \right)$.

Thus, Required percentage $ = \left[ {\dfrac{{245/3}}{{280/3}} \times 100} \right]\%  = \left( {\dfrac{{245}}{{280}} \times 100} \right)\%  = 87.5\% $.

d) What is the average sales of all the branches (in thousand numbers) for the year

\[2000?\]

Ans: Average sales of all the six branches (in thousand numbers) for the year \[2000\]

$ = \dfrac{1}{6}{\text{x}}[80 + 75 + 95 + 85 + 75 + 70]$

$ = 80$.

e) Total sales of branches ${\text{B}}1,\;\,{\text{B}}3$ and ${\text{B}}5$ together for both the years (in thousand 

numbers) is?

Ans: Total sales of branches ${\text{B}}1,\,\;{\text{B}}3$ and ${\text{B}}5$ for both the years (in thousand numbers)

$ = (80 + 105) + (95 + 110) + (75 + 95)$

$ = 560$

4. Construct a pie chart for the data given below:

Ans:

The pie chart is,

5. Answer the questions using the data from the pie chart given below:

a) Approximately how many degrees should be there in the central angle of the sector for agriculture expenditure?

Ans:In a pie chart, $100\% $ is spread over ${360^\circ }.$ 

Therefore $1\%  = {3.6^\circ }.$

Agriculture expenditure  $ = 59\% $. 

Then, $3.6 \times 59 = {212.4^\circ }$.

Therefore, ${212.4^\circ }$ should be there in the central angle of the sector for agriculture expenditure.

b) Approximately what is the ratio of expenditure on agriculture to that on dairy?

Ans:Over here, one common mistake is that students calculate the actual values of agriculture and dairy. Since budget expenditure is proportional to $\% $ of area covered, ratio of agriculture to dairy expenditure would be the ratio of corresponding $\% $ allocations. 

Therefore, $\dfrac{{{\text{Agriculture}}}}{{{\text{Diary}}}} = \dfrac{{59}}{6}$.

c) In Haryana, in \[2000\] , a total expenditure of Rs. $120\,{\text{mn}}$ was incurred. Approximately How many million did the Haryana government spend on roads?

Ans:Total expenditure $ = 100\%  = $ Rs. $120\,{\text{mn}}.$ 

Expenditure on roads $ = 9\%  = \dfrac{9}{{100}} \times 120 = {\text{Rs}}$. $10.8\,{\text{mn}}$.

Therefore, the Haryana government spend on roads about Rs. $10.8\,{\text{mn}}$.

d) If Rs. $9\,{\text{mn}}$ were spent in \[2000\] on Dairy, what would have been the total expenses in that year in million?

Ans: $9\,{\text{mn}}$ were spent on dairy. 

This amount represents $6\% $ of total expenditure in the year \[2000.\] 

$6 = $\[\left( {\dfrac{{{\text{Dairy expenditure}}}}{{{\text{Total expenditure}}}}} \right)\]$ \times 100$ 

$6 = \left( {\dfrac{{\text{9}}}{{{\text{Total}}\,{\text{expenditure}}}}} \right) \times 100$  

Total expenditure $ = 100 \times \dfrac{9}{6} = $ Rs. $150\,{\text{mn}}$

Therefore, the total expenses in that year in million is Rs. $150\,{\text{mn}}$.

5 Important Formulas from Class 8 Maths Chapter 4 Data Handling

Tips to Learn Class 8 Maths Chapter 4 Data Handling

• Start with learning key terms like mean, median, mode, range, and probability. These are the building blocks for solving problems in data handling.

• Spend time drawing bar graphs, pie charts, and histograms. Practice labelling them neatly to understand how data is visually represented.

• Try solving examples like calculating averages for cricket scores or chances of winning a game. It makes learning more practical and fun.

• Understand the concept of likelihood by working on easy examples, like rolling dice or flipping coins. This will prepare you for advanced topics later.

• Go over the important formulas and concepts frequently to keep them fresh in your memory, especially before exams.

• Practice important questions and sample problems from your textbook and reference books to gain confidence in solving different types of problems.

Benefits of CBSE Class 8 Maths Chapter 4 Data Handling Important Questions

• These important questions can be accessed online or downloaded easily and for FREE. It will help you make your practice sessions more productive.

• The solutions will help you resolve doubts on your own.

• Focus on how the experts have solved these problems in the solutions and follow the same to score more in the exams.

• These questions will act as a guide for the students throughout the learning process. It will help them to get a hold of the chapter and understand its concepts properly.

Conclusion

Important Questions for CBSE Class 8 Maths Chapter 4 Data Handling serves as a valuable resource in a student's mathematical journey. This chapter lays the foundation for essential data analysis skills, equipping students with the ability to collect, organise, and interpret data effectively. The questions presented challenge students to apply their knowledge to real-world scenarios, fostering critical thinking and problem-solving abilities. Moreover, these questions prepare students for examinations by covering a wide range of topics within data handling. They empower learners to become data-literate individuals capable of making informed decisions and finding practical applications for data analysis in various fields.

Related Study Materials for CBSE Class 8 Maths Chapter 4

CBSE Class 8 Maths Chapter-wise Important Questions

Other Important Related Links for CBSE Class 8 Maths