Courses

Courses for Kids

Free study material

Store

Talk to our experts

1800-120-456-456

CBSE

Class 9 Important Question

Maths

Chapter 13: Surface Areas And Volumes

Surface Areas and Volumes Class 9 Important Questions: CBSE Maths Chapter 11

Q: 2. The volumes of the two spheres are in the ratio 64:27. Find the ratio of their surface area.

The volume of the two spheres is in the ratio = $64:27$We know thatVolume of sphere $ = \dfrac{4}{3}\pi {r^3}$Then,$\dfrac{\text{volume of the sphere(1)}}{\text{volume of the sphere(2)}}=\dfrac{64}{27}$$ \Rightarrow\dfrac{\dfrac{4}{3}\pi {r_1^3}}{\dfrac{4}{3}\pi{r_2^3}}=\dfrac{64}{27}$$\Rightarrow\dfrac{ {r_1^3}}{{r_2^3}}=\dfrac{64}{27}$$\Rightarrow\dfrac{ {r_1}}{{r_2}}=\dfrac{4}{3}$Then, the Ratio of areas in both spheres$\dfrac{\text{Area of the sphere(1)}}{\text{Area of the sphere(2)}}=\dfrac{4\pi {r_1^2}}{4\pi {r_2^2}}$$\Rightarrow\dfrac{\text{Area of the sphere(1)}}{\text{Area of the sphere(2)}}=\dfrac{{r_1^2}}{{r_2^2}}$$\Rightarrow\dfrac{\text{Area of the sphere(1)}}{\text{Area of the sphere(2)}}=\dfrac{{4^2}}{{3^2}}$$\Rightarrow\dfrac{\text{Area of the sphere(1)}}{\text{Area of the sphere(2)}}=\dfrac{{16}}{{9}}$Hence, this is the answer.

Q: 5. If the edge of a cube is tripled, find the ratio of the surface areas of that of a volume of two cubes.

Let the edge of the cube be $x$So, the surface area of the cube is $6x^2$ and the volume will be $x^3$Now, the edge of the cube is tripled that is $3x$So, the surface area will be $6 \times (3x)^2=54x^2$ and volume will be $27x^3$ Ratio of surface areas of both cubes $\dfrac{6x^2}{54x^2}=\dfrac{1}{9}$Ratio of their volumes $\dfrac{x^3}{27x^3}=\dfrac{1}{27}$

CBSE Class 9 Maths Chapter 11 Important Questions - FREE PDF Download

Vedantu’s CBSE Class 9 Maths Chapter 11 Surface Areas and Volumes explores about 3D shape, and mainly it focuses on the surface areas and volumes of different solids like cubes, cylinders, cones, and spheres. It’s all about understanding how to calculate the area of their surfaces and the space they occupy. By practising important questions, you’ll get a strong grip on key formulas and problem-solving strategies, making it easier to tackle your exams.

CBSE Class 9 Maths Syllabus includes this chapter as an essential part of your learning, preparing you for both theoretical and application-based problems. By focusing on Class 9 Maths Important Questions, you'll be able to strengthen all the maths concepts and improve your confidence for the final exams!

Courses

Access Class 9 Maths Chapter 11: Surface Areas and Volumes Important Questions

1 Marks Questions:

1. If the perimeter of one of the faces of a cube is $40 cm$ , them its volume is

(a) $6000 c m^{3}$

(b) $1600 c m^{3}$

(d) $600 c m^{3}$ 29

Ans: (c) $1000 c m^{3}$

The perimeter of the one face of cube $= 40 cm = 4 a$

$a = \frac{40 cm}{4} = 10 cm$

Volume of the cube is $V = a^{3}$

$V = a \times a \times a$

$= 10 \times 10 \times 10$

$= 1000 c m^{3}$

2. A cuboid having surface areas of 3 adjacent faces as a, b and c has the volume

(a) $3 \sqrt{a b c}$

(b) $\sqrt{a b c}$

(d) $a^{3} b^{3} c^{3}$

Ans: (b) $\sqrt{a b c}$

Let length, width and height of cuboid be $l, w$ and $h$ respectively

Considering adjacent faces: AEHD, DHGC and EFGH

Let area of $AEHD = a$ , area of $DHGC = b$ and area of $EFGH = c$

Also, area of $AEHD = l w$

Area of $DHGC = wh$

Area of $EFGH = l h$

Therefore, $l w = a, w h = b$ and $l h = c$

$=> l w \times w h \times l h = a \times b \times c$

$=> l^{2} w^{2} h^{2} = a b c$

$\Rightarrow (l w h)^{2} = a b c$

$=> V^{2} = a b c$

$\Rightarrow V = \sqrt{a b c}$

Volume of cuboid is $V = \sqrt{a b c}$

3. The diameter of a right circular cylinder is $21 cm$ and its height is $8 cm .$ The Volume of the cylinder is

(a) $528 c m^{3}$

(b) $1056 c m^{3}$

(d) $2772 c m^{3}$

Ans: (d) $2772 c m^{3}$

Diameter of Cylinder $= 21 cm$ .

Height $= 8 cm .$

Radius $= \frac{D}{2}$

Volume of Cylinder $= (π r^{2} h)$

$V = (π) (\frac{21}{2})^{2} \times 8$

$= π \cdot {(\frac{21}{2})}^{2} \cdot 8$

$V = 2772 c m^{3}$

Volume of right circular cylinder is

4. Each edge of a cube is increased by $40 %$ . The $%$ increase in the surface area is.

(a) 40

(b) 96

(d) 240

Ans: (b) 96

Let the edge of the cube be equal to 'a' units.

Thus, the initial surface area $(A_{1}) = a^{2} u n i t s^{2}$

Now, the edge of the cube increases by $40 %$

The new edge length $= a + 40 %$ of $a = 1.4 a$ .

Thus, the final surface area $(A_{2}) = (1.4 a)^{2} = 1.96 a^{2}$ units $^{2}$

Percentage change $= [(A_{2} - A_{1}) / (A_{1})] \times 100 = [\frac{(1.96 a^{2} - a^{2})}{(a^{2})}] \times 100$

$= 0.96 \times 100$

$= 96 %$

5. Find the curved (lateral) surface area of each of the following right circular cylinders:

(a) $2 π r h$

(b) $π r h$

(d) None of these

Ans: (a) $2 π r h$

Lateral Surface Area or Curved Surface Area of a Right Circular Cylinder

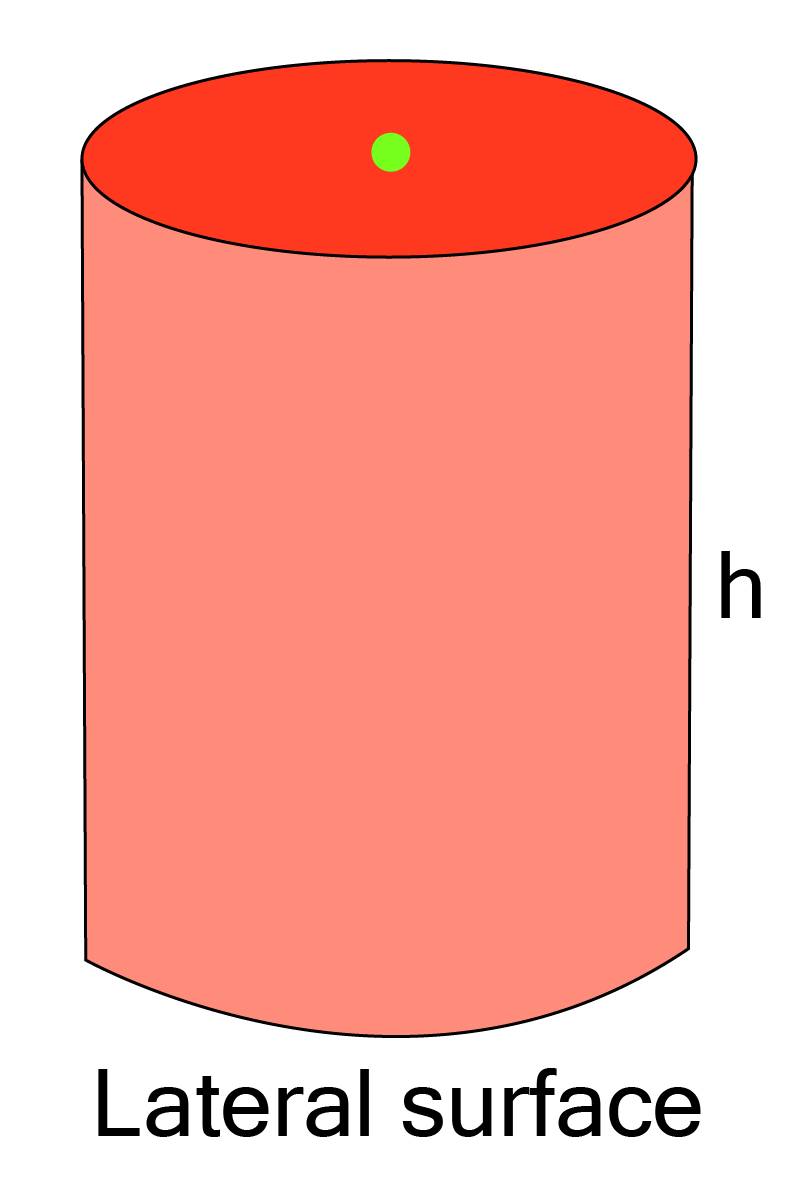
= (Perimeter of the Cross Section) × Height

= 2πrh

6. The radius and height of a right circular cylinder are each increased by $20 %$ . The volume of cylinder is increased by-

(a) $20 %$

(b) $40 %$

(d) $72.8 %$

Ans: (d) $72.8 %$

Volume $= π r^{2} h$

new radius $= r + \frac{20}{100} r$

$= \frac{6}{5} r$

$= h + \frac{20}{100} h = \frac{6}{5} h$

Volume $= π {(\frac{6 r}{5})}^{2} (\frac{6}{5} h)$

$= \frac{216}{125} π r^{2} h$

$∴$ Increase in

$Volume = \frac{216}{125} π r^{2} h$

$= 72.8 %$

7. A well of diameter 8 meters has been dug to the depth of $21 m$ . the volume of the earth dug out is

(a) $1056 cu m$

(b) $352 cu m$

(d) $4224 cu m$

Ans: (a) $1056 m^{3}$

Volume of the well is $V = π r^{2} h$

$V = π \times 4 \times 4 \times 21$

$= 1056 m^{3}$

8. The radius of a cylinder is doubled and the height remains the same. The ratio between the volumes of the new cylinder and the original cylinder is

(a) 1: 2

$(b)$ 1: 3

$(c)$ 4: 1

$(d)$ 1: 8

Ans: $(c)$ 4: 1

The radius of a cylinder is doubled and the height remains the same. (Given)

Radius of original cylinder $= r$

Radius of new cylinder $= 2 r$

Height remains the same.

We know that,

Volume of new cylinder $= π (2 r)^{2} h$

Volume of new cylinder $= 4 r^{2} π h$

Now

Let ratio of volume be " x ".

Ratio of volume = Volume of new cylinder / Volume of original cylinder

[ Put the values]

$x = 4 r^{2} π h / r^{2} π h$

$x = 4 r^{2} / r^{2}$

$\to x = 4 / 1$

The ratio between the volumes of the new cylinder and original cylinder is $4 : 1.$

9. Length of diagonals of a cube of side a cm is

(i) $\sqrt{2} a cm$

(ii) $\sqrt{3} a cm$

(iii) $\sqrt{3 a} cm$

(iv) $1 cm$

Ans: (ii) $\sqrt{3} a cm$

Diagonal of $a$ Cube $= \sqrt{3} x$

Where is the cube side.

10. Surface area of sphere of diameter $14 cm$ is

(i) $616 c m^{2}$

(ii) $516 c m^{2}$

(iii) $400 C m^{2}$

(iv) $2244 c m^{2}$

Ans: (i) $616 c m^{2}$

Given Diameter of sphere $= 14 cm$ radius $= 7 cm$

surface area of sphere $= 4 π r^{2} = 4 π (7)^{2}$

$= 4 \times 3.14 \times 49$

surface area of sphere $= 616 c m^{2}$

11. Surface area of bowl of radius $r cm$ is

(i) $4 π r^{2}$

(ii) $2 π r^{2}$

(iii) $3 π r^{2}$

(iv) $π r^{2}$

Ans: (iii) $3 π r^{2}$

The area of a circle of radius $r$ is $π r^{2}$

Thus if the hemisphere is meant to include the base then the surface area is $2 π r^{2} + π r^{2} = 3 π r^{2}$

12. Volume of a sphere whose radius $7 cm$ is

(i) $1437 \frac{1}{3} c m^{3}$

(ii) $1337 \frac{1}{3} c m^{3}$

(iii) $1430 c m^{3}$

(iv) $1447 c m^{3}$

Ans: (i) $1437 \frac{1}{3} c m^{3}$

$Radius = 7 cm$

Volume of sphere $= \frac{4}{3} π r^{3}$

$= (\frac{4}{3} \times \frac{22}{7} \times 7 \times 7 \times 7) c m^{3}$

$= (\frac{4}{3} \times 22 \times 1 \times 7 \times 7) c m^{3}$

$= \frac{4312}{3} c m^{3}$

$= 1437.33 c m^{3}$

13. The curved surface area of a right circular cylinder of height $14 cm$ is $88 c m^{2}$ . find the diameter of the base of the cylinder

(i) $1 cm$

(ii) $2 cm$

(iii) $3 cm$

(iv) $4 cm$

Ans: (ii) $2 cm$

Given, The height of cylinder $= 14 cm$

and, the curved surface area of cylinder $= 88 c m^{2}$

The curved surface area of cylinder $= 2 π rh$

and $2 r = d$

here, $r =$ radius of cylinder, $d =$ diameter of cylinder and

$h =$ height of cylinder

so, the curved surface area of cylinder $= π dh = 88 c m^{2}$

$π \times d \times 14 = 88$

$3.14 \times d \times 14 = 88$

$d = 2 cm$

so, the diameter of the cylinder is $2 cm$ .

14. Volume of spherical shell

(i) $\frac{2}{3} π r^{3}$

(ii) $\frac{3}{4} π r^{3}$

(iii) $\frac{4}{3} π [R^{3} - r^{3}]$

(iv) none of these

Ans: (iii) $\frac{4}{3} π [R^{3} - r^{3}]$

Volume of outer sphere $= \frac{4}{3} π R^{3}$

Volume of inner sphere $= \frac{4}{3} π r^{3}$

Total net volume between both the spheres $= \frac{4}{3} π (R^{3} - r^{3})$

15. The area of the three adjacent faces of a cuboid are $x, y, z$ . Its volume is $V$ , then

(i) $V = x V Z$

(ii) $V^{2} = x y z$

(iii) $V = x^{2} y^{2} z^{2}$

(iv) none of these

Ans: (ii) $V^{2} = x y z$

Let the 3 dimensions of the cuboid be $l, b$ and $h$ So,

$x = lb$

$y = bh$

$z = hl$

Multiplying above three equations,

$xyz = lb \times bh \times hl$

$= 1^{2} b^{2} h^{2}$

As,

$ $V = lbh$ $

So,

$V^{2} = l^{2} b^{2} h^{2}$

$V^{2} = xyz$

16. A conical tent is $10 m$ high and the radius of its base is $24 m$ then slant height of the tent is

(i) 26

(ii) 27

(iii) 28

(iv) 29

Ans: (i) 26

Height $(h)$ of conical tent $= 10 m$

Radius $(r)$ of conical tent $= 24 m$

Let the slant height of the tent be $l$

$l^{2} = h^{2} + r^{2}$

$l^{2} = (10)^{2} + (24)^{2}$

$l^{2} = 100 + 576$

$l^{2} = 676$

$l = \sqrt{676}$

$l = \sqrt{26^{2}}$

$l = 26 m$

Therefore, the slant height of the tent is $26 m$ .

17. Volume of hollow cylinder

(i) $π (R^{2} - r^{2}) h$

(ii) $π R^{2} h$

(iii) $π r^{2} h$

(iv) $π r^{2} (h_{1} - h_{2})$

Ans: (i) $π (R^{2} - r^{2}) h$

The formula to calculate the volume of a hollow cylinder is given as,

Volume of hollow cylinder $= π (R^{2} - r^{2}) h$ cubic units,

where, ' $R^{'}$ is the outer radius, ' $r$ ' is the inner radius, and, ' $h$ ' is the height of the hollow cylinder.

18. Diameter of the base of a cone is $10.5 cm$ and its slant height is $10 cm$ . then curved surface area.

(i) $155 c m^{2}$

(ii) $165 c m^{2}$

(iii) $150 c m^{2}$

(iv) none of these

Ans: (ii) $165 c m^{2}$

Diameter of the base of the cone is $10.5 cm$ and slant height is $10 cm$ .

Curved surface area of a right circular cone of base radius, $^{'} r^{'}$ and slant height, $l$ is $π r$ .

Diameter, $d = 10.5 cm$

Radius, $r = 10.5 / 2 cm = 5.25 cm$

Slant height, $l = 10 cm$

Curved surface area $= π rl$

$= 3.14 \times 5.25 \times 10 = 165 c m^{2}$

Thus, curved surface area of the cone $= 165 c m^{2}$ .

19. The surface area of a sphere of radius $5.6 cm$ is

Ans: Given radius of sphere $= 5.6 cm$

surface area of sphere $= 4 π r^{2}$

$= 4 \times 3.14 \times (5.6)^{2}$

surface area of sphere $= 393.88 c m^{2}$

20. The height and the slant height of a cone are $21 cm$ and $28 cm$ respectively then volume of cone

(i) $7556 c m^{3}$

(ii) $7646 c m^{3}$

(iii) $7546 c m^{3}$

(iv) none of these

Ans: (c) $7546 c m^{3}$

Volume of the cone $= \frac{1}{3} π r^{2} h$

Given

slant height $= l = 28 cm$

Height of cone $= h = 21 cm$

Let radius of cone $= r cm$

$l^{2} = h^{2} + r^{2}$

$28^{2} = 21^{2} + r^{2}$

$28^{2} - 21^{2} = r^{2}$

$r^{2} = 28^{2} - 21^{2}$

$r^{2} = (28 - 21) (28 + 21)$

$r^{2} = (7) (49)$

$r = \sqrt{7 (49)}$

$r = \sqrt{7 {(7)}^{2}}$

$r = 7 \sqrt{7} cm$

Volume of the cone $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} \times \frac{22}{7} \times 7 \sqrt{7} \times 7 \sqrt{7} \times 21 c m^{3}$

$= 22 \times 7 \sqrt{7} \times 7 \sqrt{7} c m^{3}$

$= 22 \times 7 \times 7 \times (\sqrt{7})^{2} c m^{3}$

$= 22 \times 7 \times 7 \times 7 c m^{3}$

$= 7546 c m^{3}$

2 Marks Questions:

1. A plastic box $1.5 m$ long, $1.25 m$ wide and $65 cm$ deep is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:

(i) The area of the sheet required for making the box.

Ans: (i) Given: Length $(l) = 1.5 m$ , Breadth $(b) = 1.25 m$ and Depth $(h) = 65 cm = 0.65 m$

Area of the sheet required for making the box open at the top $= 2 (b h + h l) + 1 b$

$= 2 (1.25 \times 0.65 + 0.65 \times 1.5) + 1.5 \times 1.25$

$= 2 (0.8125 + 0.975) + 1.875$

$= 2 \times 1.7875 + 1.875$

$= 3.575 + 1.875$

$= 5.45 m^{2}$

(ii) The cost of sheet for it, if a sheet measuring $1 m^{2}$ cost Rs. $20.$

Ans: Since, Cost of $1 m^{2}$ sheet = Rs. 20

cost of $5.45 m^{2}$ sheet $= 20 \times 5.45 =$ Rs. $109$

2. The length, breadth and height of a room are $5 m, 4 m$ and $3 m$ respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs. $7.50$ per $m^{2}$

Ans: Given: Length $(l) = 5 m$ , Breadth $(b) = 4 m$ and Height $(h) = 3 m$

$∵$ Area of the four walls = Lateral surface area $= 2 (b h + h l) = 2 h (b + l)$

$= 2 \times 3 (4 + 5)$

$= 2 \times 9 \times 3 = 54 m^{2}$

Area of ceiling $= l \times b = 5 \times 4 = 20 m^{2}$

$∴$ Total area of walls and ceiling of the room $= 54 + 20 = 74 m^{2}$

Now cost of white washing for $1 m^{2} =$ Rs. $7.50$

$∴$ Cost of white washing for $74 m^{2} = 74 \times 7.50 =$ Rs. $555$

3. The floor of a rectangular hall has a perimeter $250 m$ . If the cost of painting the four walls at the rate of Rs. 10 per $m^{2}$ is Rs. 15000, find the height of the hall.

Ans: Given: Perimeter of rectangular wall $= 2 (l + b) = 250 m$ . …….(i)

Now Area of the four walls of the room

$= \frac{Total cost to paint walls of the room}{Cost to paint 1 m^{2} of the walls}$

$= \frac{15000}{10} = 1500 m^{2} \dots \dots \dots$ (ii)

Area of the four walls = Lateral surface area $= 2 (b h + h l) = 2 h (b + l) = 1500$

$\Rightarrow 250 \times h = 1500$

$\Rightarrow h = \frac{1500}{250} = 6 m$

Hence required height of the hall is $6 m$ .

4. The paint in a certain container is sufficient to paint an area equal to $9.375 m^{2}$ . How many bricks of dimensions $22.5 cm \times 10 cm \times 7.5 cm$ can be painted out of this container?

Ans: Given: Length of the brick $(l) = 22.5 cm$ , Breadth $(b) = 10 cm$ and Height $(h) = 7.5 m$

$∴$ Surface area of the brick $= 2 (l b + b h + h l)$

$= 2 (22.5 \times 10 + 10 \times 7.5 + 7.5 \times 22.5)$

$= 2 (225 + 75 + 468.75)$

$= 937.5 c m^{2}$

$= 0.09375 m^{2}$

Now No. of bricks to be painted

$= \frac{Total area to be painted}{Area of one brick}$

$= \frac{9.375}{0.09375} = 100$

Hence $100$ bricks can be painted.

5. A cubical box has each edge $10 cm$ and a cuboidal box is $10 cm$ wide, $12.5 cm$ long and $8 cm$ high.

(i) Which box has the greater lateral surface area and by how much?

Ans: (i) Lateral surface area of a cube $= 4 (side)^{2} = 4 \times (10)^{2} = 400 c m^{2}$

Lateral surface area of a cuboid $= 2 h (l + b) = 2 \times 8 (12.5 + 10)$

$= 16 \times 22.5 = 360 c m^{2}$

$∴$ Lateral surface area of cubical box is greater by $(400 - 360) = 40 c m^{2}$

(ii) Which box has the smaller total surface area and how much?

(ii) Total surface area of a cube $= 6 (side)^{2} = 6 \times (10)^{2} = 600 c m^{2}$

Total surface area of cuboid $= 2 (l b + b h + h l) = 2 (12.5 \times 10 + 10 \times 8 + 8 \times 12.5)$

$= 2 (125 + 80 + 100)$

$= 2 \times 305 = 610 c m^{2}$

$∴$ Total surface area of cuboid box is greater by $(610 - 600) = 10 c m^{2}$

6. Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small and therefore negligible, how much tarpaulin would be required to make the shelter of height $2.5 m$ with base simensions $4 m \times 3 m$ ?

Ans: Given: Length of base $(l) = 4 m$ , Breadth $(b) = 3 m$ and Height $(h) = 2.5 m$

Tarpaulin required to make shelter = Surface area of 4 walls + Area of roof

$= 2 h (l + b) + l b = 2 (4 + 3) 2.5 + 4 \times 3$

$= 35 + 12 = 47 m^{2}$

Hence $47 m^{2}$ of the tarpaulin is required to make the shelter for the car.

7. The curved surface area of a right circular cylinder of height $14 cm$ is $88 c m^{2} .$ Find the diameter of the base of the cylinder.

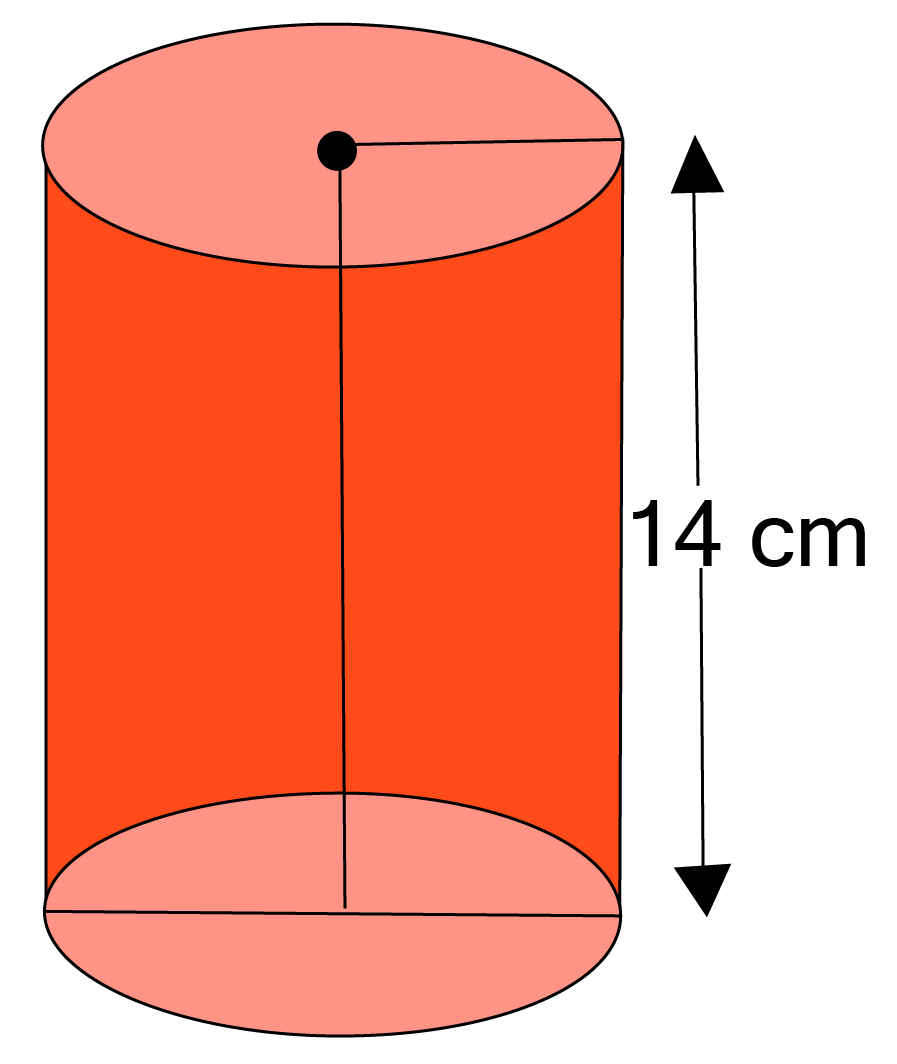
Ans: Given: Height of cylinder $(h) = 14 cm$ , Curved Surface Area $= 88 c m^{2}$

Let radius of base of right circular cylinder $= r cm$

$2 π r h = 88$

$\Rightarrow 2 \times \frac{22}{7} \times r \times 14 = 88$

$\Rightarrow r = 88 \times \frac{7}{22} \times \frac{1}{14} \times \frac{1}{2}$

$\Rightarrow r = 1 cm$

Diameter of the base of the cylinder $= 2 r = 2 \times 1 = 2 cm$

8. It is required to make a closed cylindrical tank of height $1 m$ and base diameter $140$ cm from a metal sheet. How many square meters of the sheet are required for the same?

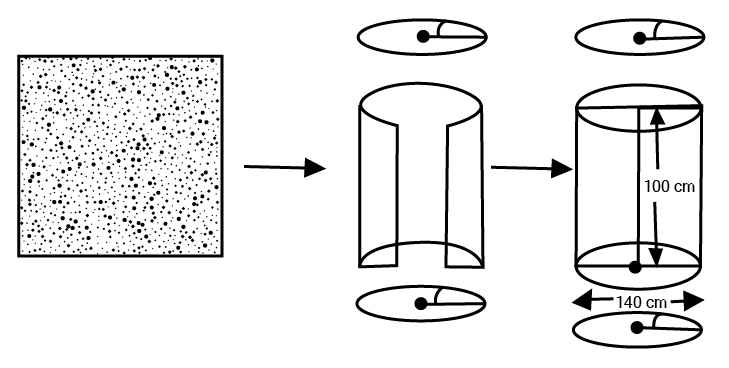
Ans: Given: Diameter $= 140 cm$

$\Rightarrow Radius (r) = 70 cm = 0.7 m$

Height of the cylinder $(h) = 1 m$

Total surface Area of the cylinder $= 2 π r (r + h) = 2 \times \frac{22}{7} \times 0.7 (0.7 + 1)$

$= 2 \times 22 \times 0.1 \times 1.7 = 7.48 m^{2}$

Hence $7.48 m^{2}$ metal sheet is required to make the close cylindrical tank.

9. The diameter of a roller is $84 cm$ and its length is $120 cm$ . It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in $m^{2}$

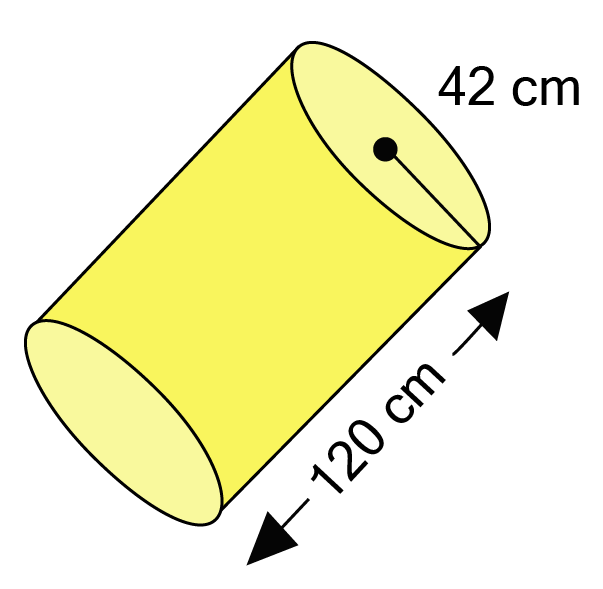
Ans: Diameter of roller $= 84 cm$

$\Rightarrow$ Radius of the roller $= 42 cm$

Length (Height) of the roller $= 120 cm$

Curved surface area of the roller $= 2 π r h$

$= 2 \times \frac{22}{7} \times 42 \times 120 = 31680 c m^{2}$

$∵$ Now area leveled by roller in one revolution $= 31680 c m^{2}$

$∴$ Area leveled by roller in $500$ revolutions $= 3.1680 \times 500 = 1584.0000$

$= 1584 m^{2}$

10. A cylindrical pillar is $50 cm$ in diameter and $3.5 m$ in height. Find the cost of white washing the curved surface of the pillar at the rate of Rs. $12.50$ per $m^{2}$

Ans: Diameter of pillar = $50 cm$

$\Rightarrow$ Radius of pillar $= 25 cm = \frac{25}{100} = \frac{1}{4} m$

Height of the pillar $= 3.5 m$

Now, Curved surface area of the pillar $= 2 π r h = 2 \frac{22}{7} \times \frac{1}{4} \times 3.5$

$= \frac{11}{2} m^{2}$

$∵$ Cost of white washing $1 m^{2} =$ Rs.12.50

$∴$ Cost of white washing $\frac{11}{2} m^{2} = \frac{11}{2} \times 12.50$

$= R s .68 .75$

11. Curved surface area of a right circular cylinder is $4.4 m^{2} .$ If the radius of the base of the cylinder is $0.7 m$ , find its height.

Ans: Curved surface area of the cylinder $= 4.4 m^{2}$ ,

Radius of cylinder $= 0.7 m$

Let height of the cylinder $= h$

$∴ 2 π r h = 4.4$

$\Rightarrow 2 \times \frac{22}{7} \times 0.7 \times h = 4.4$

$h = 4.4 \times 7 \times \frac{1}{22} \times \frac{1}{2} \times \frac{1}{0.7}$

$\Rightarrow h = 1 m$

12. The inner diameter of a circular well is $3.5 m$ . It is $10 m$ deep. Find:

(i) its inner curved surface area.

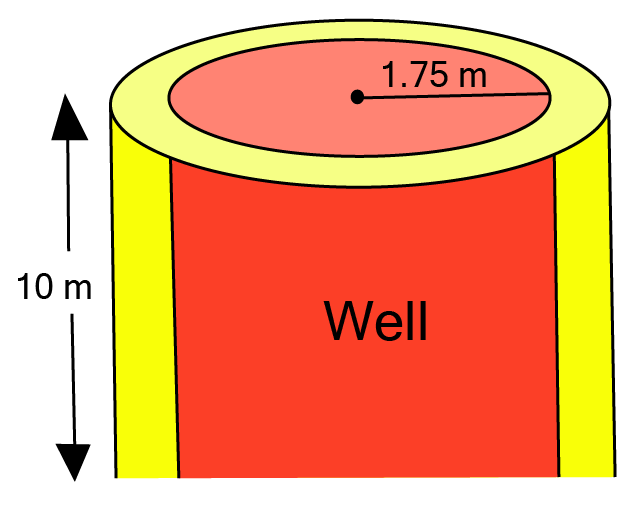
Ans: Inner diameter of circular well = $3.5 m$

$∴$ Inner radius of circular well $= \frac{3.5}{2} = 1.75 m$

And Depth of the well $= 10 m$

(i) Inner surface area of the well $= 2 π r h$

$= 2 \times \frac{22}{7} \times 1.75 \times 10 = 110 m^{2}$

(ii) the cost of plastering this curved surface at the rate of Rs. $40$ per $m^{2}$ .

Ans: Cost of plastering $1 m^{2} =$ Rs. 40

Cost of plastering $100 m^{2} = 40 \times 110 =$ Rs. $4400$

13. In a hot water heating system, there is a cylindrical piping of length $28 m$ and diameter $5 cm$ . Find the total radiating surface in the system.

Ans: The length (height) of the cylindrical pipe $= 28 m$

Diameter $= 5 cm$

$\Rightarrow Radius = \frac{5}{2} cm$

Curved surface area of the pipe $= 2 π r h = 2 \times \frac{22}{7} \times \frac{5}{2} \times 2800$

$= 44000 c m^{2} = \frac{44000}{10000} = 4.4 m^{2}$

14. In the adjoining figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of $20 cm$ and height of $30 cm$ . A margin of $2.5 cm$ is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.

Ans: Height of each of the folding at the top and bottom $(h) = 2.5 cm$

Height of the frame $(H) = 30 cm$

Diameter $= 20 cm$

$\Rightarrow$ Radius $= 10 cm$

Now cloth required for covering the lampshade

= $CSA of top part + CSA of middle part + CSA of bottom part$

$= 2 π r h + 2 π r H + 2 π r h$

$= 2 π r (h + H + h)$

$= 2 π r (H + 2 h)$

$= 2 \frac{22}{7} \times 10 (30 + 2 \times 2.5)$

$= 2200 c m^{2}$

15. The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius $3 cm$ and height $10.5 cm .$ The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?

Ans: Radius of a cylindrical pen holder $(r) = 3 cm$

Height of the cylindrical pen holder $(h) = 10.5 cm$

Cardboard required for pen holder = CSA of pen holder + Area of circular base

$= 2 π r h + π r^{2} = π r (2 h + r)$

$= \frac{22}{7} \times 3 (2 \times 10.5 + 3) = 226.28 c m^{2}$

Since Cardboard required for making 1 pen holder $= 226.28 c m^{2}$

$∴$ Cardboard required for making 35 pen holders $= 226.28 \times 35 = 7919.8 c m^{2}$

$= 7920 c m^{2} (approx .)$

16. Diameter of the base of a cone is $10.5 cm$ and its slant height is $10 cm$ . Find its curved surface area and its total surface area.

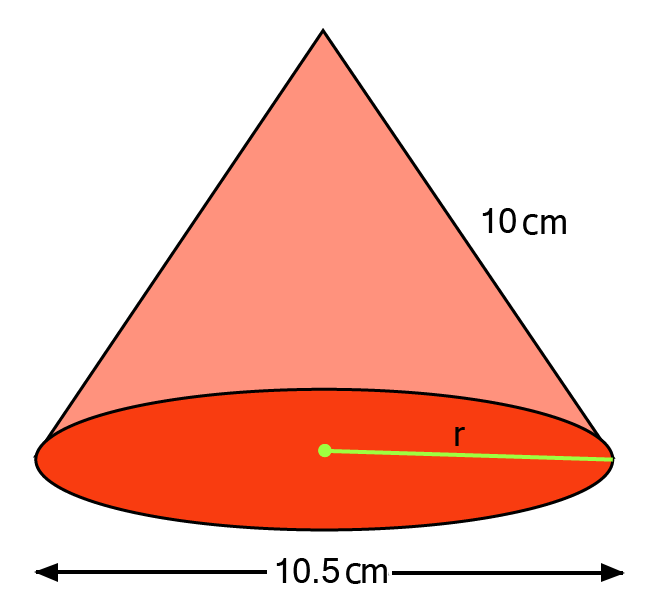
Ans: Diameter $= 10.5 cm$

$\Rightarrow Radius (r) = \frac{10.5}{2} = \frac{21}{4} cm$

Slant height of cone $(l) = 10 cm$

Curved surface area of cone $= π r l = \frac{22}{7} \times \frac{21}{4} \times 10$

$= 165 c m^{2}$

Total surface area of cone $= π r (l + r) = \frac{22}{7} \times \frac{21}{4} (10 + \frac{21}{4})$

$= \frac{22}{7} \times \frac{21}{4} \times \frac{61}{4} = 251.625 c m^{2}$

17. Find the total surface area of a cone, if its slant height is $21 cm$ and diameter of the base is $24 cm$ .

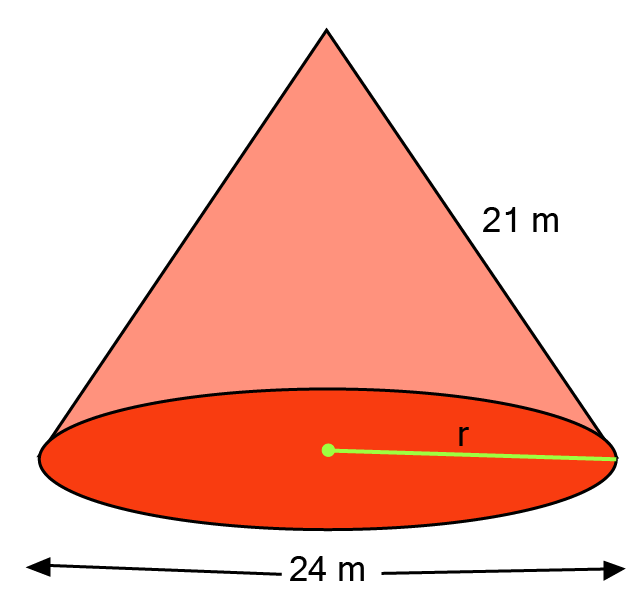
Ans: Slant height of cone $(l) = 21 m$

Diameter of cone $= 24 m$

$\Rightarrow$ Radius of cone $(r) = \frac{24}{2} = 12 m$

Total surface area of cone $= π r (l + r)$

$= \frac{22}{7} \times 12 (21 + 12)$

$= \frac{264}{7} \times 33 = 1244.57 m^{2}$

18. The slant height and base diameter of a conical tomb are $25 m$ and $14 m$ respectively. Find the cost of whitewashing its curved surface at the rate of Rs. 210 per $100 m^{2}$

Ans: Slant height of conical tomb $(l) = 25 m$ , Diameter of tomb $= 14 m$

$∴$ Radius of the tomb $(r) = \frac{14}{2} = 7 m$

Curved surface are of tomb $= π r l = \frac{22}{7} \times 7 \times 25 = 550 m^{2}$

$∵$ Cost of white washing $100 m^{2} =$ Rs. 210

$∴$ Cost of white washing $1 m^{2} = \frac{210}{100}$

$∴$ Cost of white washing $550 m^{2} = \frac{210}{100} \times 550$

$= R s . 1155$

19. A Joker's cap is in the form of a right circular cone of base radius $7 cm$ and height 24 $cm$ . Find the area of the sheet required to make 10 such caps.

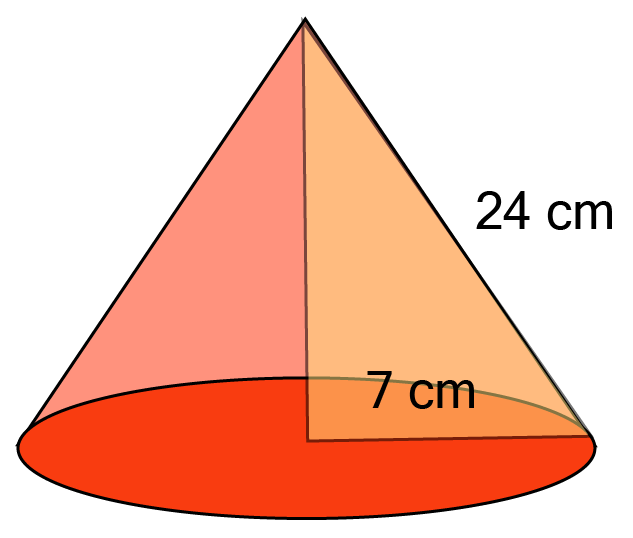
Ans: Radius of cap $(r) = 7 cm$ , Height of cap $(h) = 24 cm$

Slant height of the cone $(l) = \sqrt{r^{2} + h^{2}} = \sqrt{{(7)}^{2} + {(24)}^{2}}$

$= \sqrt{49 + 576} = \sqrt{625} = 25 cm$

Area of sheet required to make a cap = CSA of cone $= π r l$

$= \frac{22}{7} \times 7 \times 25 = 550 c m^{2}$

$∴$ Area of sheet required to make 10 caps $= 10 \times 550 = 5500 c m^{2}$

20. Find the surface area of a sphere of radius:

(i) $10.5 cm$

Ans: Radius of sphere $= 10.5 cm$

Surface area of sphere $= 4 π r^{2} = 4 \times \frac{22}{7} \times 10.5 \times 10.5$

$= 1386 c m^{2}$

(ii) $5.6 cm$

Ans: Radius of sphere $= 5.6 m$

Surface area of sphere $= 4 π r^{2} = 4 \times \frac{22}{7} \times 5.6 \times 5.6$

$= 394.84 m^{2}$

(iii) $14 cm$

Ans: Radius of sphere $= 14 cm$

Surface area of sphere $= 4 π r^{2} = 4 \times \frac{22}{7} \times 14 \times 14$

$= 2464 c m^{2}$

21. Find the surface area of a sphere of diameter:

(i) $14 cm$

Ans: (i) Diameter of sphere $= 14 cm$ ,

Therefore, Radius of sphere $= \frac{14}{2} = 7 cm$

Surface area of sphere $= 4 π r^{2} = 4 \times \frac{22}{7} \times 7 \times 7 = 616 c m^{2}$

(ii) $21 cm$

Ans: Diameter of sphere $= 21 cm$

$∴ Radius of sphere = \frac{21}{2} cm$

Surface area of sphere $= 4 π r^{2} = 4 \times \frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}$

$= 1386 c m^{2}$

(iii) $3.5 cm$

Ans: Diameter of sphere $= 3.5 cm$

$∴$ Radius of sphere $= \frac{3.5}{2} = 1.75 cm$

Surface area of sphere $= 4 π r^{2} = 4 \times \frac{22}{7} \times 1.75 \times 1.75$

$= 38.5 c m^{2}$

22. Find the total surface area of a hemisphere of radius $10 cm$ . (Use $π = 3.14$ )

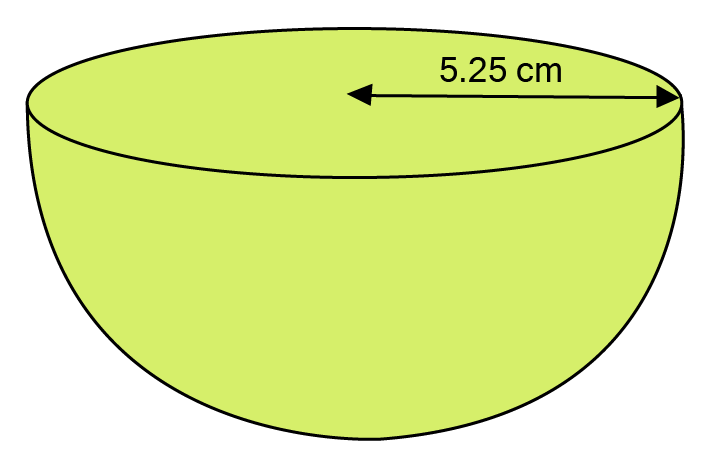
Ans: Radius of hemisphere $(r) = 10 cm$

Total surface area of hemisphere $= 3 π r^{2}$

$= 3 \times 3.14 \times 10 \times 10$

$= 942 c m^{2}$

Hence total surface area of hemisphere is $942 c m^{2}$ .

23. Find the radius of a sphere whose surface area is $154 c m^{2}$ .

Ans: Surface area of sphere $= 154 c m^{2}$

$\Rightarrow 4 π r^{2} = 154$

$\Rightarrow 4 \times \frac{22}{7} \times r^{2} = 154$

$\Rightarrow r^{2} = \frac{154 \times 7}{22 \times 4}$

$\Rightarrow r^{2} = \frac{49}{4}$

$\Rightarrow r = \frac{7}{2} = 3.5 cm$

24. A hemispherical bowl is made of steel, $0.25 cm$ thick. The inner radius of the bowl is $5 cm$ . Find the outer curved surface area of the bowl.

Ans: Inner radius of bowl $(r) = 5 cm$

Thickness of steel $(t) = 0.25 cm$

$∴$ Outer radius of bowl $(R) = r + t = 5 + 0.25 = 5.25 cm$

$∴$ Outer curved surface area of bowl $= 2 π R^{2} = 2 \times \frac{22}{7} \times 5.25 \times 5.25$

$= 2 \times \frac{22}{7} \times \frac{21}{4} \times \frac{21}{4}$

$= \frac{693}{4} = 173.25 c m^{2}$

25. A right circular cylinder just encloses a sphere of radius $r$ (See figure).

Find:

(i) Surface area of the sphere.

Ans: Radius of sphere $= r$

$∴$ Surface area of sphere $= 2 π (radius)^{2} = 2 π r^{2}$

(ii) Curved surface area of the cylinder.

Ans: The cylinder just encloses the sphere in it.

$∴$ The height of cylinder will be equal to diameter of sphere.

And The radius of cylinder will be equal to radius of sphere.

$∴$ Curved surface area of cylinder $= 2 π r h = 2 π r \times π r$

$= 4 π r^{2}$

(iii) Ratio of the areas obtained in (i) and (ii).

Ans: $\frac{Surface area of sphere}{Curved surface area of cylinder} = \frac{4 π r^{2}}{4 π r^{2}} = \frac{1}{1}$

$∴ Required ratio = 1 : 1$

26. A matchbox $4 cm \times 2.5 cm \times 1.5 cm$ . What will be the volume a packet containing 12 such boxes?

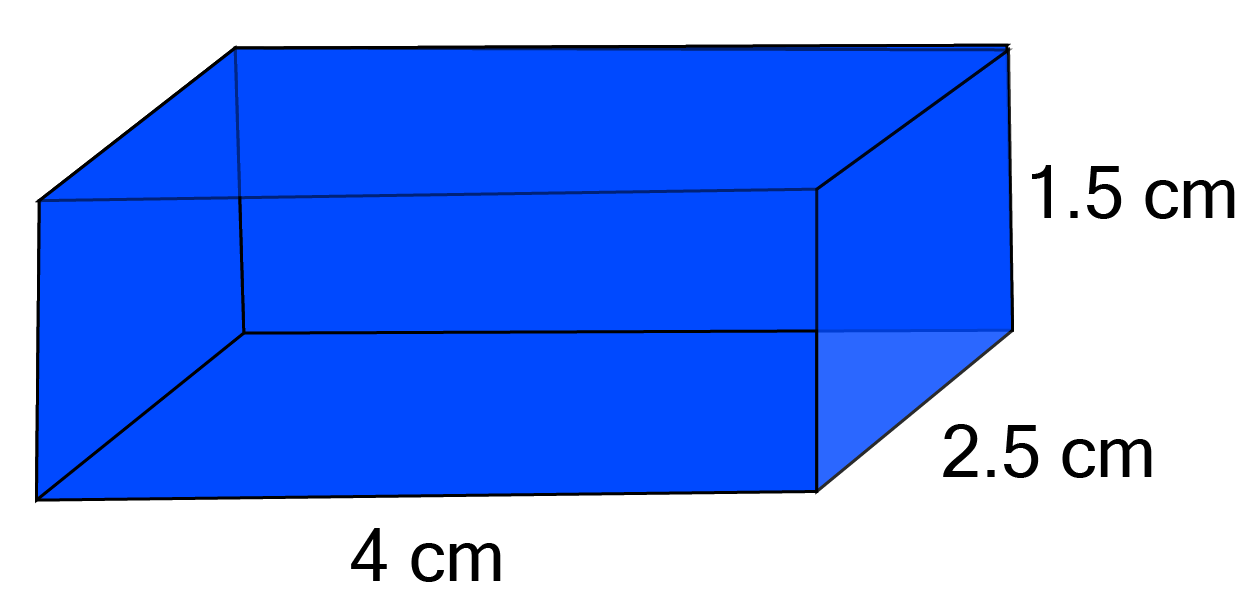
Ans: Given: Length $(l) = 4 cm$ ,

Breadth $(b) = 2.5 cm$ ,

Height $(h) = 1.5 cm$

Volume of a matchbox $= l \times b \times h$

$= 4 \times 2.5 \times 1.5$

$= 15 c m^{3}$

$∴$ Volume of a packet containing 12 such matchboxes is $180 c m^{3} .$

27. A cubical water tank is $6 m$ long, $5 m$ wide and $4.5 m$ deep. How many litres of water can it hold?

Ans: Here $l = 6 m, b = 5 m$ and $h = 4.5 m$

$∴$ Volume of the $tank = l \times b \times h$

$= (6 \times 5 \times 4.5) c m^{3}$

$= 135 m^{3}$

$= 135 \times 1 m^{3}$

$= 135 \times 1000$ litres

$= 135000$ litres

So, the cuboidal water tank can hold $135000$ litres of water.

28. A cuboidal vessel is $10 m$ long and $8 m$ wide. How high must it be to hold 380 cubic meters of a liquid?

Ans: Let height of cuboidal vessel $= h m$

Length $= 10 m$

Breadth $= 8 m$

Volume of liquid in cuboidal vessel $= 380 m^{3}$

$\Rightarrow l \times b \times h = 380 m^{3}$

$\Rightarrow 10 m \times 8 m \times h = 380$

$\Rightarrow h = \frac{380}{10 \times 8} = 4.75 m$

Hence cuboidal vessel is $4.75 m$ high.

29. Find the cost of digging a cuboidal pit $8 m$ long. $6 m$ broad and $3 m$ deep at the rate of $Rs . 30 per m^{3}$ .

Ans: Here, $l = 8 m, b = 6 m$ and $h = 3 m$

Volume of the cuboidal pit $= l b h$

$= (8 \times 6 \times 3) m^{3}$

$= 144 m^{3}$

Cost of digging $1 m^{3} = Rs 30$

Cost of digging $144 m^{3} = Rs (144 \times 30)$

$= Rs 4320$

Cost of digging the pit is $R s 4320$

30. The capacity of a cuboidal tank is $50000$ litres of water. Find the breadth of the tank, if its length and depth are respectively $2.5 m$ and $10 m .$

Ans: $Length = 2.5 m$

$Height = 10 m$

Let Breadth be b m

Capacity of cuboidal $tank = 50000$ liters

$\Rightarrow l \times b \times h = 50000 liters$

$\Rightarrow 2.5 m \times b \times 10 m = \frac{50000}{1000} m^{3}$

$\Rightarrow 25 \times b = 50$

$\Rightarrow b = 2 m$

Hence breadth of cuboidal tank is $2 m$ .

31. A river 3 m deep and $40 m$ wide is flowing at the rate of $2 km$ per hour. How much water will fall into the sea in a minute?

Ans: Water flowing in river in 1 hour = $2 km$

Water flowing in river in 1 hour $= 2000 m$

Water flowing in river in 60 minutes $= 2000 m$

Water flowing in river in 1 minute $= \frac{2000}{60} m = \frac{100}{3} m$

Now,

River is in shape of cuboid

$Length = \frac{100}{3} m$

$Breadth = 40 m$

$Height = 3 m$

Volume of water falling in the sea in 1 minute $= Volume of the cuboid$

$=$ Length $\times$ Breadth $\times$ Height

$= (\frac{100}{3} \times 40 \times 3) m^{3}$

$= (100 \times 40 \times 1) m^{3}$

$= 4000 m^{3}$

32. Find the length of a wooden plank of width $2.5 m$ , thickness $0.025 m$ and volume $0.25 m^{3}$

Ans: Given: Volume of wooden plank $= 0.25 m^{3}$

$\Rightarrow l \times 2.5 \times 0.025 = 0.25$

$\Rightarrow l = \frac{0.25}{2.5 \times 0.025}$

$\Rightarrow l = 4 m$

Hence required length of wooden plank is $4 m$ .

33. If the lateral surface of a cylinder is $94.2 c m^{2}$ and its height is $5 cm$ , then (i) radius of its base

Ans: Let radius of cylinder $= r cm$

Height $= h = 5 cm$

Now it is given that

Lateral surface $= 94.2 c m^{2}$

Curved surface area of cylinder $= 94.2 c m^{2}$

$2 π r h = 94.2$

$2 \times 3.14 \times r \times 5 = 94.2$

$r = \frac{94.2}{2 \times 3.14 \times 5}$

$r = 3 cm$

(ii) volume of the cylinder.

Ans: $r = 3 cm,$

$h = 5 cm$

Volume of cylinder $= π r^{2} h$

$= 3.14 \times 3 \times 3 \times 5$

$= 141.3 c m^{3}$

34. A bag of grain contains $2.8 m^{3}$ of grain. How many bags are needed to fill a drum of radius $4.2 m$ and height $5 m ?$

Ans: Given

Volume of grain inside the bag $= 2.8 m^{3}$

Radius of the drum $= 4.2 m$

Height of the drum $= 5 m$

$∴$ Volume of the drum $= π r^{2} h$

$= \frac{22}{7} \times (2.1)^{2} \times 5$

The number of bag full of grains required

$= \frac{Volume of the drum}{Volume of the bag}$

$= \frac{\frac{22}{7} \times 2.1 \times 2.1 \times 5}{2.8} = 99 bags$

Hence $99$ bags are needed to fill the drum.

35. A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is $7 mm$ and diameter of graphite is $1 mm$ . If the length of the pencil is $14 cm$ , find the columns of the wood and that of the graphite.

Ans: Diameter of graphite $= 1 mm$

Volume of graphite $= π r^{2} h = \frac{22}{7} \times (0.05)^{2} \times 14 = 0.11 c m^{3}$

Diameter of pencil = $7 mm$

$∴$ Radius of pencil $(R) = 3.5 mm = 0.35 cm$

Volume of pencil $= π R^{2} h = \frac{22}{7} \times (0.35)^{2} \times 14 = 5.39 c m^{3}$

Now, Volume of wood = Volume of pencil $-$ Volume of graphite

$= 5.39 - 0.11 = 5.28 c m^{3}$

36. A patient in a hospital is given soup daily in a cylindrical bowl of diameter $7 cm$ . If the bowl is filled with soup to a height of $4 cm$ , how much soup the hospital has to prepare daily to serve 250 patients?

Ans: Soup is in form of cylinder with

$Radius = r = \frac{Diameter}{2} = \frac{7}{2} cm$

$Height = h = 4 cm$

Volume of the soup in cylindrical bow $= π r^{2} h$

$= \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 4 c m^{3}$

$= 154 c m^{3}$

Soup served to 1 patient $= 154 c m^{3}$

Soup served to 250 patients $= 250 \times 154 c m^{3}$

$= 38500 c m^{3}$

$= 38500 \times \frac{1}{1000}$ litres

$= 38.5$ litres

37. Find the volume of the right circular cone with:

(i) Radius $6 cm$ , Height $7 cm$

Ans: Given: $r = 6 cm, h = 7 cm$

Volume of cone $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} \times \frac{22}{7} \times 6 \times 6 \times 7$

$= 264 c m^{3}$

(ii) Radius $3.5 cm$ , Height $12 cm$

Ans: Given: $r = 3.5 cm, h = 12 cm$

Volume of cone $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 12$

$= 154 c m^{3}$

38. The height of a cone is $15 cm$ . If its volume is $1570 c m^{3}$ , find the radius of the base.

Ans: Height of cone $= h = 15 cm$

Let radius of cone $= r cm$

Given

Volume of cone $= 1570 c m^{3}$

$\frac{1}{3} \times 3.14 \times r^{2} \times 15 = 1570$

$1 \times 3.14 \times r^{2} \times 5 = 1570$

$r^{2} = \frac{1570}{3.14 \times 5}$

$r^{2} = 100 r$

$= \sqrt{100} r = \sqrt{{(10)}^{2}}$

$r = 10 cm$

Hence required radius of the base is $10$ cm.

39. If the volume of a right circular cone of height $9 cm$ is $48 π c m^{3}$ , find the diameter of the base.

Ans: Height of the cone $(h) = 9 cm$

Let radius of cone $= rcm$

Given Volume of cone $= 48 π c m^{3}$

$\frac{1}{3} π r^{2} h = 48 π$

$\Rightarrow \frac{1}{3} π r^{2} h = 48 π$

$\Rightarrow \frac{1}{3} π r^{2} \times 9 = 48 π$

$\Rightarrow 3 r^{2} = 48$

$\Rightarrow r^{2} = \frac{48}{3} = 16$

$\Rightarrow r = 4 cm$

$∴$ Diameter of base $= 2 r = 2 \times 4 = 8 cm$

40. A conical pit of top diameter $3.5 m$ is $12 m$ deep. What is its capacity in kiloliters?

Ans: Height of conical pit $= h = 12 m$

Radius of conical pit $= r = \frac{Diameter}{2} = \frac{3.5}{2} m = 1.75 m$

$Capacity of pit = Volume of cone = \frac{1}{3} π r^{2} h$

$= (\frac{1}{3} \times \frac{22}{7} \times 1.75 \times 1.75 \times 12) m^{3}$

$= 38.5 m^{3}$

$= 38.5$ kiloliters

Since $1 m^{3} = 1 k l$

Capacity of pit $= 38.5$ kiloliters.

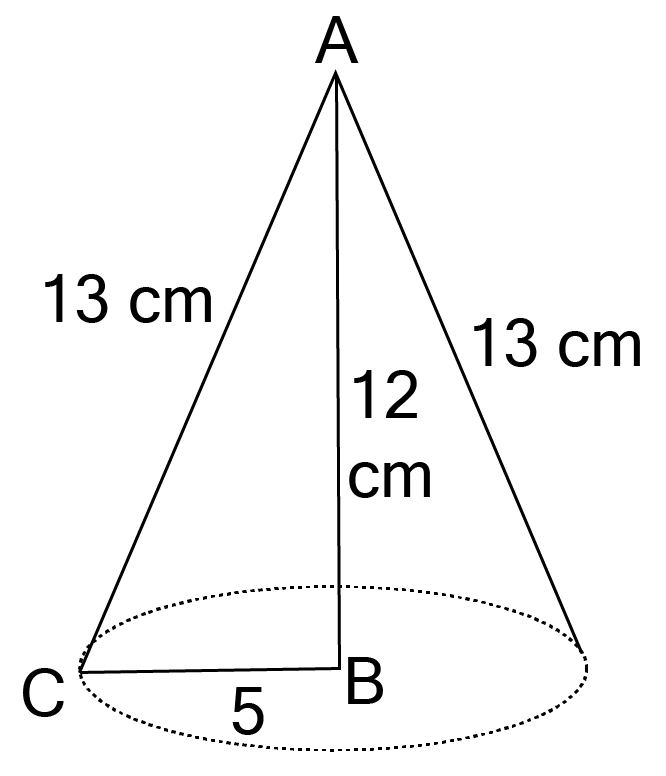
41. A right triangle ABC with sides $5 cm, 12 cm$ and $13 cm$ is revolved about the side 12 $cm$ . Find the volume of the solid so obtained. (Use $π = 3.14$ )

Ans: When right angled triangle $ABC$ is revolved about side $12 cm$ , then the solid formed is a cone.

In that cone, Height $(h) = 12 cm$

And radius $(r) = 5 cm$

Therefore, Volume of cone $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} π \times 5 \times 5 \times 12$

$= 100 π c m^{3}$

42.Find the volume of the largest right circular cone that can be fitted in a cube whose edge is $14 cm$ .

Ans: For largest circular cone radius of the base of the cone $= \frac{1}{2}$ edge of cube

$= \frac{1}{2} \times 14 = 7 c m$

And height of the cone $= 14 cm$

Volume of cone $= \frac{1}{3} \times 3.14 \times 7 \times 7 \times 14$

$= 718.666 c m^{3}$

43. Find the volume of a sphere whose radius is

(i) $7 cm$

Ans: Radius of sphere $(r) = 7 cm$

Volume of sphere $= \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times 7 \times 7 \times 7$

$= \frac{4312}{3} = 1437 \frac{1}{3} c m^{3}$

(ii) $0.63 cm$

Ans: Radius of sphere $(r) = 0.63 m$

$Volume of sphere = \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times 0.63 \times 0.63 \times 0.63$

$= \frac{4}{3} \times \frac{22}{7} \times \frac{63}{100} \times \frac{63}{100} \times \frac{63}{100}$

$= 1.047816 m^{3} = 1.05 m^{3} (approx .)$

44. Find the amount of water displaced by a solid spherical ball of diameter:

(i) $28 cm$

Ans: Diameter of spherical ball = $28 cm$

$∴$ Radius of spherical ball $(r) = \frac{28}{2} = 14 cm$

According to question, Volume of water replaced = Volume of spherical ball $= \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times 14 \times 14 \times 14$

$= \frac{34496}{3} = 11498 \frac{2}{3} c m^{3}$

(ii) $0.21 m$

Ans: Diameter of spherical ball $= 0.21 m$

$∴$ Radius of spherical ball $(r) = \frac{0.21}{2} m$

According to question,

Volume of water replaced = Volume of spherical ball $= \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times \frac{0.21}{2} \times \frac{0.21}{2} \times \frac{0.21}{2}$

$= \frac{4}{3} \times \frac{22}{7} \times \frac{21}{200} \times \frac{21}{200} \times \frac{21}{200}$

$= 11 \times \frac{441}{100 \times 100 \times 100} = 0.004851 m^{3}$

45. The diameter of a metallic ball is $4.2 cm$ . What is the mass of the ball, if the metal weighs $8.9 g$ per $c m^{3} ?$

Ans: Diameter of metallic ball $= 4.2 cm$

$∴$ Radius of metallic ball $(r) = \frac{4.2}{2} = 2.1 cm$

Volume of metallic ball $= \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 2.1$

$= \frac{4}{3} \times \frac{22}{7} \times \frac{21}{10} \times \frac{21}{10} \times \frac{21}{10} = 38.808 c m^{3}$

Density of metal $= 8.9 g$ per $c m^{3}$

Mass of $38.808 c m^{3} = 8.9 \times 38.808$

$= 345.3912 g = 345.39 g$

46. A hemispherical tank is made up of an iron sheet $1 cm$ thick. If the inner radius is 1 $m$ , then find the volume of the iron used to make the tank.

Ans: Inner radius $= r_{1} = 1 m$

$Outer radius = r_{2} = 1 m + 1 cm$

$= 1 m + \frac{1}{100} m$

$= 1 m + 0.01 m$

$= 1.01 m$

Volume of iron used $=$ Volume of outer hemisphere $-$ Volume of inner hemisphere

Volume of iron of hemisphere $= \frac{2}{3} π [R^{3} - r^{3}]$

$= \frac{2}{3} \times \frac{22}{7} \times [{(101)}^{3} - {(100)}^{3}]$

$= \frac{44}{21} [1030301 - 1000000]$

$= 0.06348 m^{3}$

47. A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of Rs. $498.96 .$ If the cost of white-washing is at the rate of Rs. $2.00$ per square meter, find:

(i) the inner surface area of the dome.

Ans: Cost of white washing from inside $= R s .498 .96$

Rate of white washing $= R s .2$

Area white washed $= \frac{498.96}{2} = 249.48 c m^{2}$

Therefore, inner surface area of dome $= 249.48 m^{2}$

(ii) the volume of the air inside the dome.

Ans: Volume of air inside dome = Volume of hemisphere $= \frac{2}{3} π r^{3}$

Let the radius of dome $= r m$

First we find radius using surface area

Surface area of dome $= 249.48 m^{2}$

$2 π r^{2} = 249.48$

$2 \times \frac{22}{7} \times r^{2} = 249.48$

$r^{2} = \frac{249.48 \times 7}{2 \times 22}$

$r^{2} = 39.69$

$r = \sqrt{39.69}$

$∴ r = 6.3 m$

Volume of the air inside the dome $=$ volume of hemisphere

$= \frac{2}{3} π r^{3}$

$= \frac{2}{3} \times \frac{22}{7} \times 6.3 \times 6.3 \times 6.3 m^{3}$

$= 523.908 m^{3}$

48. Twenty-seven solid iron spheres, each of radius $r$ and surface area $S$ are melted to form a sphere with surface area $S$ '. Find the:

(i) radius $r$ ' of the new sphere.

Ans: Volume of 1 sphere, $V = \frac{4}{3} π r^{3}$

Volume of $27$ solid sphere

$= 27 \times \frac{4}{3} π r^{3}$

Let $r_{1}$ is the radius of the new sphere.

Volume of new sphere $=$ Volume of $27$ solid sphere

$\frac{4}{3} π r_{1}^{3} = 27 \times \frac{4}{3} π r^{3}$

$\frac{r_{1}^{3}}{r^{3}} = 27$

$\frac{r_{1}}{r} = \sqrt[3]{27}$

$\frac{r_{1}}{r} = \frac{3}{1}$

$r_{1} = 3 r$

(ii) ratio of $S$ and $S$ '.

Ans: $\frac{Surface area of new sphere S_{1}}{Surface area of old sphere S}$

$\frac{S_{1}}{S} = \frac{4 π r_{1}^{2}}{4 π r^{2}}$

$\frac{S_{1}}{S} = \frac{{(3 r)}^{2}}{r^{2}}$

$\frac{S_{1}}{S} = \frac{9 r^{2}}{r^{2}}$

$\frac{S_{1}}{S} = \frac{9}{1}$

$S_{1} : S = 9 : 1$

$S : S_{1} = 1 : 9$

49. A capsule of medicine is in the shape of a sphere of diameter $3.5 mm$ . How much medicine (in $m m^{3}$ ) is needed to fill this capsule?

Ans: Diameter of spherical capsule = $3.5 mm$

$∴$ Radius of spherical capsule $(r) = \frac{3.5}{2} = \frac{35}{20} = \frac{7}{4} mm$

Medicine needed to fill the capsule = Volume of sphere

$= \frac{4}{3} π r^{3} = \frac{4}{3} \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times \frac{7}{4}$

$= \frac{11 \times 7 \times 7}{3 \times 2 \times 4} = \frac{539}{34} m m^{3}$

$= 22.46 m m^{3}$

50. Sameera wants to celebrate the fifth birthday of her daughter with a party. She bought thick paper to make the conical party caps. Each cap is to have a base diameter of $10 cm$ and height $12 cm$ . A sheet of the paper is $25 cm$ by $40 cm$ and approximately $82 %$ of the sheet can be effectively used for making the caps after cutting. What is the minimum number of sheets of paper that Sameera would need to buy, if there are to be $15$ children at the party? (Use $π = 3.14)$

Ans: Diameter of base of conical cap = $10 cm$

$∴$ Radius of conical cap $(r) = 5 cm$

Slant height of cone $(l) = \sqrt{r^{2} + h^{2}}$

$= \sqrt{{(5)}^{2} + {(12)}^{2}}$

$= \sqrt{25 + 144} = \sqrt{169}$

$= 13 cm$

Curved surface area of a cap $= π r l$

$= 3.14 \times 5 \times 13 = 204.1 c m^{2}$

Curved surface area of a cap $= π r l$

$= 3.14 \times 5 \times 13 = 204.1 c m^{2}$

Curved surface area of 15 caps $= 15 \times 204.1 = 3061.5 c m^{2}$

Area of a sheet of paper used for making caps $= 25 \times 40 = 1000 c m^{2}$

$82 %$ of sheet is used after cutting $= 82 %$ of $1000 c m^{2}$

$= \frac{82}{100} \times 1000 = 820 c m^{2}$

Number of sheet $= \frac{3061.5}{820} = 3.73$

Hence $4$ sheets area needed.

51. Curved surface area of a right circular cylinder is $4.4 s q m$ . if the radius of the base of the cylinder is $0.7 m$ find its height.

Ans: Let the height of the circular cylinder be $h$ .

Radius $(r)$ of the base of cylinder $= 0.7 m$

Curved Surface Area of cylinder $= 2 π r h$

$4.4 m^{2} = 2 π r h$

$4.4 m^{2} = (2 \times \frac{22}{7} \times 0.7 \times h) m$

$\frac{44}{10} m = (2 \times \frac{22}{7} \times \frac{7}{10} \times h)$

$44 m = (2 \times 22 \times h)$

$h = \frac{44}{2 \times 22}$

$h = 1 m$

Therefore, the height of the cylinder is $1 m$ .

52. The circumference of the trunk of a tree (cylindrical), is $44 dm$ . Find the volume of the timber obtained from the trunk if the length of the trunk is $5 m .$

Ans: Let $r$ be the radius of the cylindrical Trunk

Circumference of the trunk $= 44 dm$

Converting dm into $m$ ,

$44 d m = 4.4 m$

The circumference is $C = 2 π r$

$4.4 = 2 \times 3.14 \times r$

$r = \frac{4.4}{2 \times 3.14}$

$r = 0.7$

The height is $h = 5 m$

The volume of the cylinder is

$V = π r^{2} h$

$V = 3.14 \times {0.7}^{2} \times 5$

$V = 7.693 m^{3}$

Therefore, the volume of the trunk is $7.693$ cubic meter.

53. If the areas of three adjacent faces of a cuboids are $X, Y$ and $Z .$ If its volume is $V$ , prove that $V^{2} = XYZ$

Ans: Areas of three faces of cuboid as $x, y, z$

So, Let length of cuboid be $= l$

Breadth of cuboid be $= b$

Height of cuboid be $= h$

Let, $x = l \times b$

$y = b \times h$

$z = h \times l$

Else write as

$x y z = l^{2} b^{2} h^{2} \dots . . (i)$

If ' $V^{'}$ is volume of cuboid $= V = l b h$

$V^{2} = l^{2} b^{2} h^{2} = x y z \dots \dots$ from (i)

$∴ V^{2} = xyz$

Hence proved.

54. Find the volume of an iron bar has in the shape of cuboids whose length, breadth and height measure $25 cm .$ $18 cm$ and $6 cm$ respectively. Find also its weight in kilograms if 1 cu cm of iron weight 100 grams.

Ans: Length of the bar $= 25 cm$

Breadth of the bar $= 18 cm$

Height of the $b a r = 6 cm$

$∴$ Volume of the iron bar $= l \times b \times h$ cu unit

$= (25 \times 18 \times 6) cu cm$

$= 2700 cu cm$

Weight of the bar $= (2700 \times 100) gm$

$= 270000 gm$

$= 270 kg$

55. A rectangular piece of paper is $22 cm$ long and $12 cm$ wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.

Ans: It is clear that circumference of the base of the cylinder = length of the paper Let $rcm$ be the radius of the base of the cylinder and its height as $hcm$ .

$∴ 2 π r = 22 and h = 12 cm$

$2 \times \frac{22}{7} \times r = 22$

$r = \frac{7}{2} cm$

Volume of the cylinder $= π r^{2} h$

$= \frac{22}{7} \times {(\frac{7}{2})}^{2} \times 12 cu cm$

$= \frac{22 \times 7 \times 7 \times 12}{7 \times 2 \times 2} cu cm$

$= 462 cu cm .$

56. If the radius of the base of a right circular cylinder is halved, keeping the height same, find the ratio of the volume of the reduced cylinder to that of original cylinder.

Ans: Let the radius of the original cylinder $= r$ units

Height of the original cylinder $= h$ units

$∴$ volume of the cylinder $= π r^{2} h$ cu units $\to$ (i)

Radius of the reduced cylinder $= \frac{r}{2}$ units

Height of the reduced cylinder $= h$ units

$∴$ volume of the reduced cylinder $= π {(\frac{r}{2})}^{2} h$ cu units

$= \frac{π r^{2} h}{4} cu units \to (2)$

From (i) and (ii) we get

$\frac{volume of cylinder (reduced)}{volume of the original cylinder} = \frac{π r^{2} h}{π r^{2} h 4}$

$= \frac{1}{4}$

Thus, there required ratio $= 1 : 4$

57. A rectangle tank measuring $5 m$ by $4.5 m$ by $2.1 m$ is dug in the centre of a field $25 m$ by $13.5 m .$ The earth dug out is spread evenly over the remaining portion of the field. How much is the level of the field raised?

Ans: Volume of the tank $= 5 \times 4.5 \times 2.1 cum$

$= 47.25 cm$

$∴$ Volume of the earth $dug = 47.25 cum$

Area of the field $= 25 \times 13.5$

$= 337.5 sqm$

$∴$ Remaining area of the field $= (337.5 - 22.5)$

$= 315 sq m$

$∴$ Level of the field raised $= \frac{volume of the earth dug out}{remaining area of the field}$

$= \frac{47.25}{315} m = \frac{4725}{315} cm$

$= 15 cm$

58. A village having a population of $4000$ requires $150$ litres of water per head per day. It has a water tank measuring $20 m \times 15 m \times 6 m$ which is full of water. For how many days will the water tank last?

Ans: Number of days water will last

$= \frac{Volume of tank}{Total water required per day}$

Here, $l = 20 m, b = 15 m$ and $h = 6 m$

Volume of the tank $= l \times b \times h$

$= (20 \times 15 \times 6) m^{3}$

$= 1800 m^{3}$

Water required per person per day $= 150$ litres

Water required for 4000 person per day $= (4000 \times 150)$ litres

$= 4000 \times 150 \times (\frac{1}{1000}) m^{3}$

$= 600 m^{3}$

$Number of days water will last = \frac{Volume of tank}{Total water required per day}$

$= (\frac{1800 m^{3}}{600 m^{3}})$

$= 3$

Thus, the water will last for $3$ days.

59. Find the curved surface area of a right circular cone whose slant height is $10 cm$ and base radius is $7 cm$

Ans: Curved surface area $= π r l$

$= \frac{22}{7} \times 7 \times 10 c m^{2}$

$= 220 c m^{2}$

60. Find (i) the curved surface area

Ans: The curved $π r l$ surface area of hemisphere of radius $21 cm$ would be $= 2 π r^{2}$

$= 2 \times \frac{22}{7} \times 21 \times 21 c m^{2}$

$= 2772 c m^{2}$

(ii) Total surface area of a hemisphere of radius $21 cm$

Ans: The total surface area of the hemisphere $= 3 π r^{2}$

$= 3 \times \frac{22}{7} \times 21 \times 21 c m^{2}$

$= 4158 c m^{2}$

61. The circumference of the base of a cylindrical vessel is $132 cm$ and its height is 25 $cm$ How many litres of water can it hold? $[1000 c m^{3} = 1 l]$

Ans: Given circumference of base of cylindrical vessel $= 132 cm$

$2 π r = 132 cm$

$r = \frac{132}{2 π} = \frac{66^{3}}{22} \times 7 = 21 cm$

Number of liters of water $= π r^{2} h$

$= \frac{22}{7} \times 21 \times 21 \times 25 c m^{3}$

$= 22 \times 3 \times 21 \times 25 c m^{3}$

$= 34650 c m^{3}$

$= 34650 \times (\frac{1}{1000})$ litres

$= 34.65$ litres

Vessel can hold $34.65$ litres.

62. A cubical box has each edge $10 cm$ and another cuboidal box is $12.5 cm$ long, $10 cm$ wide and $8 cm$ high. Which box has the greater lateral surface area and by how much?

Ans: Side of cubical box $= 10 cm$

Lateral surface area of cube $= 4 a^{2}$

$4 \times 10^{2} = 400 c m^{2}$

Length of cuboidal box $= 12.5 cm$ .

Breadth $= 10 cm$

Height $= 8 cm$

Lateral surface area $= 2 [l + b] h$

$= 2 [12.5 + 10] 8$

$= 16 \times 22.5 = 360 c m^{2}$

$Difference = 400 - 360 = 40 c m^{2}$

Lateral surface area of cuboidal box is greater by $40 c m^{2}$

63. A hemi spherical bowl has a radius of $3.5 cm$ . What would be the volume of water it would contain?

Ans: The volume of water the bowl contain $= \frac{2}{3} π r^{3}$

Radius of hemisphere $= r = 3.5 cm$

The volume of water the bowl can contain $= \frac{2}{3} π r^{3}$

$= \frac{2}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 3.5 c m^{3}$

$= 89.8 c m^{3}$

64. A conical pit of top diameter $3.5 m$ is $12 m$ deep. What is its capacity in kiloliters

Ans: Diameter of conical Pit $= 3.5 m$

Height of conical pit $= h = 12 m$

Radius of conical pit $= r = \frac{Diameter}{2}$

$= \frac{3.5}{2} m = 1.75 m$

Capacity of pit $=$ Volume of cone

$= \frac{1}{3} π r^{2} h$

$= (\frac{1}{3} \times \frac{22}{7} \times 1.75 \times 1.75 \times 12) m^{3}$

$= 38.5 m^{3}$

$= 38.5$ kiloliters

Capacity of pit $= 38.5$ kiloliters.

65. The diagonals of a cube is $30 cm$ , find its volume

Ans: Let side of cube be a cm

$Diagonal = \sqrt{3} a$

$\sqrt{3} a = 30$

$a = \frac{30}{\sqrt{3}}$

Volume of cube $= a^{3} = {(\frac{30}{\sqrt{3}})}^{3}$

$= \frac{27000}{3 \sqrt{3}} = \frac{9000}{\sqrt{3}} c m^{3}$

66. A cylindrical tank has a capacity of $6160 m^{3}$ find its depth if the diameter of the base is $28 m$

Ans: Diameter of the base = $28 m$

Radius $r = \frac{28}{2} = 14 m$

$Volume = π r^{2} h = 6160$

$\frac{22}{7} \times 14 \times 14 \times h = 6160$

$h = \frac{6160 \times 7}{22 \times 14 \times 14} = 10 m$

Hence depth of tank $= 10 m$

67. Find the volume of a sphere whose surface area is $154 c m^{2}$

Ans: Given surface area of sphere $= 154 c m^{2}$

Let radius of the sphere $= r cm$

$4 π r^{2} = 1544 \times \frac{22}{7} \times r^{2}$

$= 154 r^{2}$

$= \frac{154 \times 7}{4 \times 22} r^{2}$

$= 12.25 r$

$= \sqrt{12.25} r$

$= 3.5 cm$

Volume of sphere $= \frac{4}{3} π r^{3}$

$= (\frac{4}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 3.5) c m^{3}$

$= 179.67 c m^{3}$

68. If the volume of a right circular cone of height $9 cm$ is $48 π c m^{3}$ Find the diameter of its base

Ans: Given volume of cone $= 48 π c m^{3}$ and height $= 9 cm$

Volume of cone $= 48 π c m^{3}$

$\frac{1}{3} π r^{2} h = 48 π$

$\frac{1}{3} π r^{2} \times (9) = 48 π$

$π r^{2} 3 = 48 π$

$r^{2} = \frac{48 π}{3 π}$

$r^{2} = 16$

$r = \sqrt{16}$

$r = \sqrt{{(4)}^{2}}$

$r = 4 cm$

$Diameter = 2 \times Radius$

$= 2 \times 4 = 8 cm$

Thus, the diameter of the base of cone is $8 cm$ .

69. The volume of a cylinder is $69300 c m^{3}$ and its height is $50 cm .$ Find its curved surface area

Ans: Volume $= π r^{2} h = 69300$ and $h = 50 cm$

$\Rightarrow \frac{22}{7} \times r^{2} \times 50 = 69300$

$r^{2} = \frac{69300 \times 7}{22 \times 50} = 441$

$r = \sqrt{441} = 21 cm$

$∴$ Curved surface area $= 2 π r h$

$= 2 \times \frac{22}{7} \times 21 \times 50 = 6600 c m^{2}$

70. The volume of a cube is $1000 c m^{3}$ , Find its total surface area.

Ans: Volume $= a^{3} = 1000 c m^{3}$

$a = 10 cm$

Total surface area $= 6 a^{2} = 6 \times 100$

$= 600 c m^{2} .$

3 Marks Questions:

1. A small indoor green house (herbarium) is made entirely of glass panes (including base) held together with tape. It is $30 cm$ long, $25 cm$ wide and $25 cm$ high.

(i) What is the surface area of the glass?

Ans: Length $(l)$ of green house $= 30 cm$

Breadth $(b)$ of green house $= 25 cm$

Height $(h)$ of green house $= 25 cm$

The green house is cuboid and Glass is on the all 6 sides of cuboid greenhouse

Area of glass = Surface area of green house

$= 2 [l b + l h + b h]$

$= [2 (30 \times 25 + 30 \times 25 + 25 \times 25)] c m^{2}$

$= [2 (750 + 750 + 625)] c m^{2}$

$= (2 \times 2125) c m^{2}$

$= 4250 c m^{2}$

Hence $4250 c m^{2}$ of the glass is required to make a herbarium.

(ii) How much of tape is needed for all the 12 edges?

Ans: Tape is used at $12$ edges.

$\Rightarrow$ Tape is used at 4 lengths, 4 breadths and 4 heights.

$\Rightarrow$ Total length of the tape $= 4 (l + b + h)$

$= 2 (30 + 25 + 25)$

$= 320 cm$

Hence $320 cm$ of the tape if needed to fix $12$ edges of herbarium.

2. A metal pipe is $77 cm$ long. The inner diameter of a cross section is $4 cm$ , the outer diameter being $4.4 cm$ . [See fig.]. Find its:

(i) Inner curved surface area

Ans:

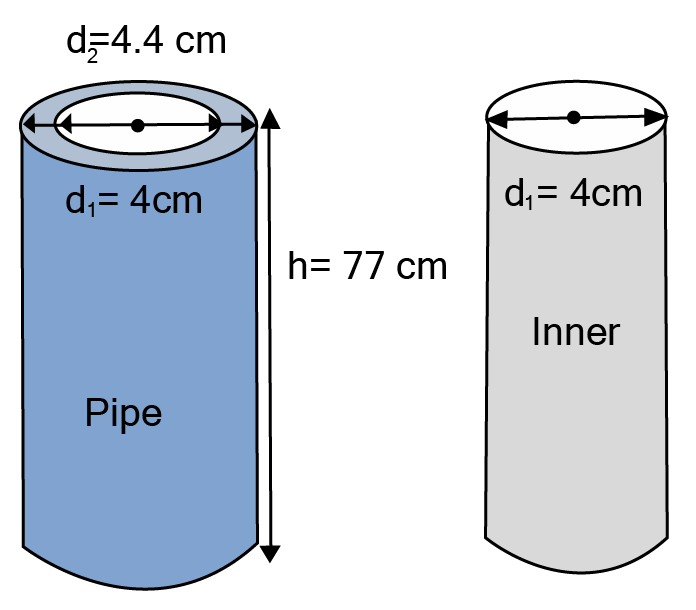
Inner diameter of cross-section $= 4 cm$

Inner radius of cylindrical pipe $= r_{1} = \frac{Inner diameter}{2}$

$= (\frac{4}{2}) cm = 2 cm$

Height $(h)$ of cylindrical pipe $= 77 cm$

Curved Surface Area of inner surface of pipe $= 2 π r_{1} h$

$= (2 \times \frac{22}{7} \times 2 \times 77) c m^{2}$

$= 968 c m^{2}$

Inner curved surface area is $968 c m^{2}$

(ii) Outer curved surface area

Ans: Outer diameter of pipe $= 4.4 cm$

Outer radius of cylindrical pipe $= r_{2} = \frac{Outer diameter}{2}$

$= (\frac{4.4}{2}) cm = 2.2 cm$

Height of cylinder $= h = 77 cm$

Curved Surface Area of outer surface of pipe $= 2 π r_{2} h$

$= (2 \times \frac{22}{7} \times 2.2 \times 77) c m^{2}$

$= (2 \times 22 \times 2.2 \times 11) c m^{2}$

$= 1064.8 c m^{2}$

Outer curved surface area is $1064.8 c m^{2}$

(iii) Total surface area

Ans: $r_{1} = 2 cm$

$r_{2} = 2.2 cm$

$h = 77 cm$

Total surface area $=$ Curved Surface Area of inner cylinder $+$ Curved Surface Area of outer cylinder $+ 2 \times$ Area of base

$Area of base = Area of circle with radius 2.2 cm - Area of circle with radius 2 cm$

$= π r_{2}^{2} - π r_{1}^{2}$

$= \frac{22}{7} \times ({(2.2)}^{2} - {(2)}^{2})$

$= \frac{22}{7} \times (4.84 - 4)$

$= \frac{22}{7} \times (0.84)$

$= 2.64 c m^{2}$

Total surface area = Curved Surface Area of inner cylinder $+$ Curved Surface Area of outer cylinder $+ 2 \times$ Area of base

$= 968 + 1064.8 + 2 \times 2.64$

$= 2032.8 + 5.28$

$= 2038.08 c m^{2}$

Therefore, the total surface area of the cylindrical pipe is $2038.08 c m^{2}$

3. Curved surface area of a cone is $308 c m^{2}$ and its slant height is $14 cm$ . Find

(i) radius of the base

Ans: Slant height of cone $(l) = 14 cm$

Curved surface area of cone $= 308 c m^{2}$

$π r l = 308$

$\frac{22}{7} \times r \times 14 = 308$

$22 \times r \times 2 = 308$

$r = (\frac{308}{2 \times 22}) cm$

$∴ r = 7 cm$

Therefore, the radius of the circular end of the cone is $7 cm$ .

(ii) total surface area of the cone.

Ans: Total surface area of the cone = Curved surface area + Area of circular base

$= 308 + π r^{2}$

$= 308 + \frac{22}{7} \times (7)^{2}$

$= 462 c m^{2}$

Therefore, the total surface area of the cone is $462 c m^{2}$ .

4. A conical tent is $10 m$ high and the radius of its base is $24 m$ . Find:

(i) slant height of the tent.

Ans: Height of the conical tent $(h) = 10 m$

Radius of the conical tent $(r) = 24 m$

Let the slant height of the tent be $l$

Slant height of the tent $l^{2} = h^{2} + r^{2}$

$l^{2} = (10)^{2} + (24)^{2}$

$l^{2} = 100 + 576$

$l^{2} = 676$

$l = \sqrt{676}$

$l = \sqrt{26^{2}}$

$l = 26 m$

Therefore, the slant height of the tent is $26 m$ .

(ii) cost of the canvas required to make the tent, if the cost of a $m^{2}$ canvas is $Rs . 70 .$

Ans: Here the tent does not cover the base, So, find curved surface area of tent Curved surface area of tent $= π r l$

Here, $r = 24 m, l = 26 m$

Curved surface area of tent $= π r l$

$= (\frac{22}{7} \times 24 \times 26) m^{2}$

$= \frac{13728}{7} m^{2}$

Cost of $1 m^{2}$ canvas $=$ Rs 70

Cost of $\frac{13728}{7} m^{2} canvas$ $= Rs (\frac{13728}{7} \times 70)$

$= Rs 137280$

Therefore, the cost of the canvas required to make the tent is $R s 137280$

5. What length of tarpaulin $3 m$ wide will be required to make conical tent of height $8 m$ and base radius $6 m$ ? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately $20 cm$ . (Use $π = 3.14)$

Ans: Height of the conical tent $(h) = 8 m$ and Radius of the conical tent $(r) = 6 m$

Slant height of the tent $(l) = \sqrt{r^{2} + h^{2}}$

$= \sqrt{{(6)}^{2} + {(8)}^{2}}$

$= \sqrt{36 + 64}$

$= \sqrt{100} = 10 m$

Area of tarpaulin $=$ Curved surface area of tent $= π r l$

$= 3.14 \times 6 \times 10 = 188.4 m^{2}$

Width of tarpaulin $= 3 m$

Let Length of $tarpaulin = L$

$∴$ Area of tarpaulin $=$ Length $\times$ Breadth

$= L \times 3 = 3 L$

Now, According to question, $3 L = 188.4$

$\Rightarrow L = \frac{1884.4}{3} = 62.8 m$

The extra length of the material required for stitching margins and cutting is $20 cm = 0.2 m$ .

So, the total length of tarpaulin bought is $(62.8 + 0.2) m = 63 m$

6. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of $40 cm$ and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per $m^{2}$ , what will be the cost of painting all these cones? (Use $π = 3.14$ and take $\sqrt{1.04} = 1.02)$

Ans: Curved surface area of cone will be painted $= π rl$

$h = 1 m;$ $radius = \frac{40}{2} = 20 cm = 0.2 m$

and let 1 be the slant height,

$∴ 1^{2} = h^{2} + r^{2} = 1^{2} + {0.2}^{2}$

$\Rightarrow 1 = \sqrt{1 + 0.04} = \sqrt{1} .04 = 1.02 m$

$\Rightarrow$ Curved surface area of 1 cone $= π rl$

$= (3.14 \times 0.2 \times 1.02) m^{2} = 0.64046 m^{2}$

$\Rightarrow$ Curved surface area of 50 cones $= 50 \times 0.64046 = 32.028 m^{2}$

Cost of painting $1 m^{2} =$ Rs. 12

$∴$ Cost of painting $32.028 m^{2} = (12 \times 32.028)$

$= 384.336 m^{2} \approx 384.34$

$∴$ Cost of painting 50 cones is Rs. $384.84$ .

7. The radius of a spherical balloon increases from $7 cm$ to $14 cm$ as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.

Ans: I case: Radius of balloon $(r) = 7 cm$

Surface area of balloon $= 4 π r^{2} = 4 π \times 7 \times 7 c m^{2} \dots \dots \dots . .$ (i)

II case: Radius of balloon (R) = $14 cm$

Surface area of balloon $= 4 π R^{2} = 4 π \times 14 \times 14 c m^{2} \dots \dots \dots . .$ (ii)

Now, Ratio [from eq. (i) and (ii)],

$\frac{CSA in first case}{CSA in second case} = \frac{4 π \times 7 \times 7}{4 π \times 14 \times 14} = \frac{1}{4}$

Hence, required ratio $= 1 : 4$

8. A village having a population of $4000$ requires $150$ litres of water per head per day. It has a tank measuring $20 m$ by $15 m$ by $6 m$ . For how many days will the water of this tank last?

Ans: Capacity of cuboidal tank $= l \times b \times h = 20 m \times 15 m \times 6 m$

$= 1800 m^{3}$

$= 1800 \times 1000$ liters

$= 1800000$ liters

Water required by her head per day $= 150$ liters

Water required by 4000 persons per day $= 150 \times 4000 = 600000$ liters

Number of days the water will last $= \frac{Capacity of tank (in liter)}{Total water required per day (in liters)}$

$= \frac{1800000}{600000} = 3$

Hence water of the given tank will last for $3$ days.

9. A godown measures $40 m \times 25 m \times 15 m$ . Find the maximum number of wooden crates each measuring $1.5 m \times 1.25 m \times 0.5 m$ that can be stored in the godown.

Ans: Capacity of cuboidal godown $= 40 m \times 25 m \times 15 m = 15000 m^{3}$

Capacity of wooden crate $= 1.5 m \times 1.25 m \times 0.5 m = 0.9375 m^{3}$

Maximum number of crates that can be stored in the godown $= \frac{Volume of godown}{Volume of one crate}$

$= \frac{15000}{0.9375} = 16000$

Hence maximum $16000$ crates can be stored in the godown.

10. Find the minimum number of bricks each measuring $22.5 cm \times 11.5 cm \times 7.5 cm$ required to construct a wall $10 m$ long, $6 m$ high and $1.5 m$ thick.

Ans: Volume of one cuboidal brick $= l \times b \times h$

$= 22.5 cm \times 11.5 cm \times 7.5 c m^{3}$

$= 1940.625 c m^{3}$

$= 0.001940625 m^{3}$

Volume of cuboidal wall $= 10 m \times 6 m \times 1.5 m$

$= 90 m^{3}$

$Minimum number of bricks required = \frac{Volume of wall}{Volume of a brick}$

$= \frac{90}{0.001940625}$

$= \frac{90}{\frac{1940625}{1000000000}}$

$= \frac{90000000000}{1940625} = 46376.81$

$= 46377$ [Since bricks cannot be in fraction]

11. The circumference of the base of a cylindrical vessel is $132 cm$ and its height is $25 c m$ How many litres of water can it hold?

Ans: Height of vessel $= (h) = 25 cm$

Circumference of base of vessel = $132 cm$

$\Rightarrow 2 π r = 132$

$\Rightarrow 2 \times \frac{22}{7} \times r = 132$

$r = \frac{132 \times 7}{2 \times 22} = 21 cm$

Now, Volume of cylindrical vessel $= π r^{2} h$

$= \frac{22}{7} \times 21 \times 21 \times 35 = 34650 c m^{3}$

$= \frac{34650}{1000}$ liters

$= 34.65$ liters

12. The inner diameter of a cylindrical wooden pipe is $24 cm$ and its out diameter is $28 cm$ . The length of the pipe is $35 cm$ . Find the mass of the pipe, if $1 c m^{3}$ of wood has a mass of $0.5 g$

Ans: Inner diameter of pipe $= 28 cm$

$∴$ Inner radius of pipe $(r) = \frac{24}{2} = 12 cm$

And Outer diameter of pipe $= 28 cm$

$∴$ Outer radius of pipe $(R) = \frac{28}{2} = 14 m$

Length of pipe $(h) = 35 cm$

Volume of wood $=$ Volume of outer cylinder $-$ Volume of inner cylinder

$= π R^{2} h - π r^{2} h = π h (R^{2} - r^{2})$

$= \frac{22}{7} \times 35 [{(14)}^{2} - {(12)}^{2}]$

$= 110 [196 - 144] = 110 \times 52 = 5720 c m^{3}$

$∵$ Weight of $1 c m^{3}$ of wood $= 0.6 g$

$∴$ Weight of $5720 c m^{3}$ of wood $= 0.6 \times 5720$

$= 3432 g = 3.432 kg$

Therefore, mass of pipe is $3.432 kg$

13. A soft drink is available in two packs (i) a tin can with a rectangular base of length $5 cm$ and width $4 cm$ , having height of $15 cm$

Ans: Given, Length $= 5 cm$

Width $= 4 cm$

Height $= 15 cm$

Volume of the tin can $V = l \times b \times h$

$= 5 \times 4 \times 15 = 300 c m^{3}$

(ii) a plastic cylinder with circular base of diameter $7 cm$ and height $10 cm$ . Which container has greater capacity and how much?

Ans: Given, Diameter $= 7 cm$ , Height $= 10 cm$ $π = \frac{7}{2}$ Volume $= π r^{2} h$

$= \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$

$Difference = 385 c m^{3} - 300 c m^{3} = 85 c m^{3}$

Hence, Cylinder container has greater capacity by $85$ cubic cm.

14. It costs $Rs . 2200$ to paint the inner curved surface of a cylindrical vessel $10 m$ deep. If the cost of painting is at the rate of Rs. $20$ per $m^{2}$ , find:

(i) inner curved surface area of the vessel.

Ans: Total cost to paint inner curved surface area of the vessel $= Rs . 2200$

Rate $= R s . 20$ per square meter

Inner curved surface area of vessel $= \frac{Total cost}{Rate}$

$= \frac{2200}{20} = 110 m^{2}$

(ii) radius of the base.

Ans: Depth of the vessel $(h) = 10 m$

Now, Inner surface area of vessel $= 110 m^{2}$

$\Rightarrow 2 π r h = 110$

$\Rightarrow 2 \times \frac{22}{7} \times r \times 10 = 110$

$\Rightarrow r = \frac{110 \times 7}{2 \times 22 \times 10} = 1.75 m$

(iii) capacity of the vessel.

Ans: Since $r = 1.75 m$ and $h = 10 m$

$∴$ Capacity of vessel $=$ Volume of cylinder $= π r^{2} h$

$= \frac{22}{7} \times 1.75 \times 1.75 \times 10 = 96.25 m^{3}$

$= 96.25 kl$

15. The capacity of a closed cylindrical vessel of height $1 m$ is $15.4$ litres. How many square meters of metal sheet would be needed to make it?

Ans: Height of the vessel $(h) = 1 m$

Capacity of vessel $= 15.4$ liters

$= \frac{15.4}{1000}$ kilo liters

$= 0.0154 m^{3}$

$\Rightarrow π r^{2} h = 0.0154$

$\Rightarrow \frac{22}{7} \times r^{2} \times 1 = 0.0154$

$\Rightarrow r^{2} = \frac{0.0154 \times 7}{22}$

$\Rightarrow r^{2} = 0.0007 \times 7 = 0.0048$

$\Rightarrow r = 0.07 m$

$Now, Area of metal sheet required = TSA of cylindrical vessel$

$= 2 π r (r + h)$

$= 2 \times \frac{22}{7} \times 0.07 (1 + 0.07)$

$= \frac{44}{7} \times 0.07 \times 1.07$

$= 0.4708 m^{2}$

16. Find the capacity of a conical vessel with:

(i) Radius $7 cm$ , Slant height $25 cm$

Ans: Given: $r = 7 cm, l = 25 cm$

$h = \sqrt{l^{2} - r^{2}}$

$= \sqrt{{(25)}^{2} - {(7)}^{2}}$

$= \sqrt{625 - 49}$

$= \sqrt{576} = 24 cm$

Capacity of conical vessel $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 24 = 1232 c m^{3}$

$= 1.232$ liters

(ii) Height $12 cm$ , Slant height $13 cm$

Ans: Given: $h = 12 cm, l = 13 cm$

$r = \sqrt{l^{2} - h^{2}} = \sqrt{{(13)}^{2} - {(12)}^{2}}$

$= \sqrt{169 - 144}$

$= \sqrt{25} = 5 cm$

Capacity of conical vessel $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} \times \frac{22}{7} \times 5 \times 5 \times 12 = \frac{2200}{7} c m^{3}$

$= \frac{2200}{7} \times \frac{1}{1000}$ liters

$= \frac{11}{35} liter$

17. If the triangle ABC in question 7 above is revolved about the side $5 cm$ , then find the volume of the solid so obtained. Find, also, the ratio of the volume of the two solids obtained.

Ans: When right angled triangle $ABC$ is revolved about side $5 cm$ , then the solid formed is a cone.

In that cone, Height $(h) = 5 cm$

And radius $(r) = 12 cm$

Therefore, Volume of cone $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} π \times 12 \times 12 \times 5$

$= 240 π c m^{3}$

Now, $\frac{Volume of cone in Q . No . 7}{Volume of vone in Q . No . 8} = \frac{100 π}{240 π} = \frac{5}{12}$

$∴$ Required ratio $= 5 : 12$

18. The diameter of the moon is approximately one-fourth the diameter of the earth. What fraction is the volume of the moon of the volume of the earth?

Ans: Let diameter of earth be $x$

$∴$ Radius of earth $(r) = \frac{x}{2}$

Now, Volume of earth $= \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times π \times \frac{x}{2} \times \frac{x}{2} \times \frac{x}{2} = \frac{1}{8} \times \frac{4}{3} π x^{3}$

According to question,

Diameter of moon $= \frac{1}{4} \times$ Diameter of earth

$= \frac{1}{4} \times x = \frac{x}{4}$

Radius of moon $(R) = \frac{x}{8}$

Now, Volume of Moon $= \frac{4}{3} π R^{3}$

$= \frac{4}{3} \times π \times \frac{x}{8} \times \frac{x}{8} \times \frac{x}{8} = \frac{1}{512} \times \frac{4}{3} π x^{3}$

$= \frac{1}{64} \times [\frac{1}{8} \times \frac{4}{3} π x^{3}]$

$= \frac{1}{64} \times Volume of Earth$

Volume of moon is $\frac{1}{64} t h$ the volume of earth.

19. How many litres of milk can a hemispherical bowl of diameter $10.5$ hold?

Ans: Diameter of hemispherical bowl = $10.5 cm$

$∴$ Radius of hemispherical bowl $(r) = \frac{10.5}{2} = 5.25 cm$

Volume of milk in hemispherical bowl $= \frac{2}{3} π r^{3}$

$= \frac{2}{3} \times \frac{22}{7} \times 5.25 \times 5.25 \times 5.25$

$= \frac{2}{3} \times \frac{22}{7} \times \frac{525}{100} \times \frac{525}{100} \times \frac{525}{100}$

$= 11 \times \frac{21}{4} \times \frac{21}{4} = 303.187 c m^{3}$

$= \frac{303.187}{1000}$ liters

$= 0.303187$ liters $= 0.303$ liters

20. Find the volume of a sphere whose surface area is $154 c m^{2}$ .

Ans: Surface area of sphere $= 154 c m^{2}$

$\Rightarrow 4 π r^{2} = 154$

$\Rightarrow 4 \times \frac{22}{7} \times r^{2} = 154$

$\Rightarrow r^{2} = \frac{154 \times 7}{4 \times 22} = \frac{49}{4}$

$\Rightarrow r = \frac{7}{2} cm$

Now, Volume of sphere $= \frac{4}{3} π r^{3} = \frac{4}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times \frac{7}{2}$

$= \frac{1}{3} \times 11 \times 49 = \frac{539}{3}$

$= 179 \frac{2}{3} c m^{3}$

21. A wooden bookshelf has external dimensions as follows: Height $= 110 cm$ , Depth $= 25$ cm, Breadth $= 85 cm$ . The thickness of the planks is $5 cm$ everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is $20$ paise per $c m^{2}$ and the rate of painting is $10$ paise per $c m^{2}$ , find the total expenses required for polishing and painting the surface of the bookshelf

Ans: External faces to be polished

$=$ Area of six faces of cuboidal bookshelf $- 3$ (Area of open portion ABCD)

$= 2 (110 \times 25 + 25 \times 85 + 85 \times 110) - 3 (75 \times 30)$

$= 2 (2750 + 2125 + 9350) - 3 \times 2250$

$= 2 \times 14225 - 6750$

$= 28450 - 6750$

Now, cost of painting outer faces of wodden bookshelf at the rate of $20$ paise.

$= Rs . 0.20 per c m^{2}$

$= Rs . 0.20 \times 21700 = Rs . 4340$

Here, three equal five sides inner faces.

Therefore, total surface area $= 3 [2 (30 + 75) 20 + 30 \times 75]$ [ Depth $= 25 - 5 = 20 cm]$

$= 3 [2 \times 105 \times 20 + 2250] = 3 [4200 + 2250]$

$= 3 \times 6450 = 19350 c m^{2}$

Now, cost of painting inner faces at the rate of 10 paise i.e. Rs. $0.10$ per $c m^{2}$ .

$= R s 0.10 \times 19350 = Rs . 1935$

22. If diameter of a sphere is decreased by $25 %$ then what percent does its curved surface area decrease?

Ans: Diameter of original sphere $= D = 2 R$

$\Rightarrow R = \frac{D}{2}$

Curved surface area of original sphere $= 4 π R^{2}$

$= 4 π {(\frac{D}{2})}^{2} = π D^{2}$

According to the question, Decreased diameter $= 25 %$ of $D = \frac{25}{100} D$

$= \frac{D}{4}$

$∴$ Diameter of new sphere $= D - \frac{D}{4} = \frac{3 D}{4}$

$∴$ Radius of new sphere $= \frac{3 D}{8}$

Now, curved surface area of new sphere $= 4 π r^{2} = 4 π {(\frac{3 D}{8})}^{2}$

$= \frac{9 π}{16} D^{2}$

Change in curved surface area $= π D^{2} - \frac{9 π}{16} D^{2}$

$= \frac{7}{16} π D^{2}$

Percent change in the curved surface area $= \frac{Change in curved surface area}{Curved surface area of origianal sphere}$ $\times 100$ $= \frac{7}{\frac{7}{16} π D^{2}} π D^{2} \times 100$

$= \frac{7}{16} \times 100 = 43.75 %$

23. The surface area of cuboids is $3328 m^{2}$ ; its dimensions are in the ratio $4 : 3 : 2.$ Find the volume of the cuboid.

Ans: Let the dimensions of the cuboid be $4 x, 3 x$ and $2 x$ meters

Surface area of the cuboid $= 2 (4 x \times 3 x + 3 x \times 2 x + 2 x \times 4 x) s q m$

$= 2 (12 x^{2} + 6 x^{2} + 8 x^{2}) s q m$

$= 52 x^{2} s q m \to (i)$

Given surface area $= 3328 sq m$

From (i) and (ii) we get

$52 x^{2} = 3328$

or $x^{2} = \frac{3328}{52} = 64$

or $x = 8$

$∴ 4 x = 32, 3 x = 24 and 2 x = 16$

Thus, the dimensions of the cuboid are $32 m, 24 m$ and $16 m$

$∴$ Volume of the cuboid $= (32 \times 24 \times 16) m^{3}$

$= 12288 cu m$

24. The volume of a rectangular slower of stone is $10368 d m^{3}$ and is dimensions are in the ratio of 3:2:1. (i) Find the dimensions (ii) Find the cost of polishing its entire surface @ Rs. 2 per $d m^{2}$ .

Ans: Let the length of the block be $3 x d m$

Width $= 2 \times d m$ and height $= x dm$

Volume of the block $= 10368 d m^{3}$

$∴ 3 x \times 2 x \times x = 10368$

or $x^{3} = \frac{10368}{6}$

$= 1728$

$∴ x = \sqrt[3]{1728}$

$= \sqrt[3]{12 \times 12 \times 12}$ $= 12$

also $2 x = 24$ and $3 x = 36$

Thus, dimensions of the block are $36 dm, 24 dm$ and $12 dm$

Surface area of the block $= 2 (36 \times 24 + 24 \times 12 + 36 \times 12) d m^{2}$

$= 2 (864 + 288 + 432) d m^{2}$

$= 2 \times 1584 d m^{2}$

$= 3168 d m^{2}$

Cost of polishing the surface $= R s (2 \times 3168)$

$= Rs . 6336$

25. In a cylindrical drum of radius $4.2 m$ and height $3.5 m$ , how many full bags of wheat can be emptied if the space required for each bag is $2.1 cum$ .

Ans: Radius of the drum $= 4.2 m = \frac{42}{10} m$

Height of the drum $= 3.5 m = \frac{35}{10} m$

$∴$ Volume of the drum $= π r^{2} h$ cu units

$= (\frac{22}{7} \times \frac{42}{10} \times \frac{42}{10} \times \frac{35}{10}) cu m \dots . . (i)$

Volume of wheat in each bags $= 2.1 cu m = \frac{21}{10} cu m$

$= \frac{volume of drum}{volume of wheat in each bag}$

$= \frac{\frac{22}{7} \times \frac{42}{10} \times \frac{42}{10} \times \frac{35}{10}}{\frac{21}{10}}$

$= \frac{924}{10} = 92.4$

$= 92$

Hence the number of full bags is $92$ .

26. The inner diameter of a cylindrical wooden tripe is $24 cm .$ and its outer diameter is $28 cm$ . the length of wooden tripe is $35 cm$ . find the mass of the tripe, if $1 cu cm$ of wood has a mass of $0.6 g$ .

Ans: Inside diameter of the pipe $= 24 cm$

Outside diameter of the pipe $= 28 cm$

Length of the pipe $= 35 cm = h$

Outside radius of the pipe $= \frac{28}{2} cm = 14 cm = R$ $Volume of the wood = External volume - Internal volume$

$= π r^{2} h - π^{2} l$

$= π \times 35 (14^{2} - 12^{2}) cu cm$

$= \frac{22}{7} \times 35 (14 + 12) (14 - 12) cu cm$

$= 5720 cu cm$

Mass of $1 cu cm = 0.6 g$

$∴$ Mass of the pipe $= (0.6 \times 5720) g$

$= 3432 g$

$= 3.432 kg$

27. A patient in a hospital is given soup daily in a cylindrical bowl of a diameter $7 cm$ . If the bowl is filled with soup to height of $4 cm .$ How much soup the hospital has to prepare daily to serve $250$ patients?

Ans: Diameter of the bowl $= 7 cm$ .

Radius of the bowl $= \frac{7}{2} cm$

Height up to which soup is filled $(h) = 4 cm$ .

Volume of the soup in one bowl $= π r^{2} h$

$= \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 4 cu cm$

$= 154 cu cm$

$∴$ soup given to one patient $= 154 cu cm$ .

Soup given to 250 patients $= 250 \times 154 cu cm$

$= 38500 cu cm$

$= \frac{38500}{1000} ltrs$

$= 38.5 ltrs .$

Hence the hospital has to prepare $38.5$ litre daily to serve $250$ patients.

28. The diameter of a roller is $84 cm$ and its length is $120 cm .$ It takes $500$ complete revolutions to move once over to level a playground.

(a) Find the area of playground in sq $m$ .

Ans: $R =$ Radius of the roller $= \frac{84}{2}$

Area $= 42 cm = 0.42 m$

$H =$ length of the roller $= 120 cm . = 1.2 m$ .

Area covered in the revolution $= 2 π r h s q$ unit

$= \frac{2 \times 22 \times 0.42 \times 1.2}{7}$

$= 3.168 sq m$

$∴$ Area covered in 500 revolutions $= 500 \times 3.168$ sq $m$

$= 1584 sq m$

Thus, area of playground $= 1584 sqm$ .

(b) Determine the cost of leveling the playground at the rate of Rs $1.75$ per sq $m$ .

Ans: cost of leveling 1 sq $m$ . of playground $= R s 1.75$

Cost of total leveling $= Rs (1584 \times 1.75)$

$= Rs 2772$

29. A metal cube of edge $12 cm$ is melted and formed into three similar cubes. If the edge of two smaller cubes is $6 cm$ and $8 cm$ , find the edge of the third smaller cube (Assuming that there is no loss of metal during melting).

Ans: Volume of cube with edge $12 cm = (12)^{3}$ cu $cm$ .

$= 1728 cu cm . . . . . . . . . (1)$

Volume of the first smaller cube with edge $6 cm = (6)^{3} cu cm$

$= 216 cu cm . . . . . . . . (2)$

Volume of the second smaller cube with edge $8 cm . = (8)^{3} cu cm$

$= 512 cu cm . \dots . . . (3)$

Let the edge of the third smaller cube be a $cm$ .

$∴$ Volume of the third smaller cube $== 9^{2} c m^{3} . . . . . . . . (4)$

$216 + 512 + a^{3} = 1728$ [using (1) and (2)]

By the given condition.

area $728 a^{3} = 1728$

Area $a^{3} = 1728 - 728 = 1000 = (10)^{3}$

$∴ a = 10$

Thus, the edge of the third required cube is $10 cm$ .

30. How many bricks, each measuring $18 cm$ by $12 cm$ by $10 cm$ will be required to build a wall $15 m$ long $6 dm$ wide and $6.5 m$ high when $\frac{1}{10}$ of its volumes occupied by mastar? Please find the cost of the bricks to the nearest rupees, at Rs $1100$ per $1000$ bricks.

Ans: Length of the wall $= 15 m . = 1500 cm$ .

Width of the wall $= 6 dm . = 60 cm$ .

Height of the wall $= 6.5 m . = 650 cm$ .

$∴$ Volume of the wall $= (1500 \times 60 \times 650) cu cm$

$= 58500000 cu cm . \to (I)$

Volume occupied by master $= (\frac{1}{10} \times 58500000) cu cm$

$= 5850000 cu cm . \to$ (ii)

$∴$ Volume occupied by bricks $= (i) - (i i)$

$= (58500000 - 5850000) cu cm$

$= 52650000 cu cm . \to$ (iii)

Volume of a brick $= (18 \times 12 \times 10) cu cm$

$= 2160 cu cm . \to$ (iv)

$∴$ No of brick required

$= \frac{52650000}{2160}$

$= 24375$

cost of 1000 bricks = Rs 1100

Total cost $= Rs \frac{24375 \times 1100}{1000}$

$= R s 26812.50$

31. A river $3 m$ deep and $40 m$ wide is flowing at the rate of $2 km$ per hour. How much will fall into the sea in a minute?

Ans: Depth of river $= 3 m$

Water of the river $= 40 m$

Rate of flow of water $= 2 km / hr = 2000 m / hr$

$∴$ Volume of water flowing in one hour

$= 2000 \times 40 \times 3$

$= 240000 m^{3}$

Hence, Volume of water flowing in one minute $= \frac{240000}{60} = 4000 m^{3}$

32. If the lateral surface of a cylinder is $94.2 c m^{2}$ and its height is $5 cm$ . then find

(i) radius of its base

Ans: Given lateral surface of cylinder $= 94.2 c m^{2}$

$2 π r h = 94.2 c m^{2}$

$H = 5 cm$

$2 π r \times 5 = 94.2$

$r = \frac{94.2}{10 π} = \frac{94.2}{10 \times 3.14} cm$

$R = 3 cm$

(ii) its volume $[π = 3.14]$

Ans: Volume of cylinder $= π r^{2} h$

$= 3.14 \times 3^{2} \times 5$

$= 141.3 c m^{3}$

33. A shot put is a metallic sphere of radius $4.9 cm$ If the density of the metal is $7.8 g$ per $c m^{3}$ Find the mass of the shot put.

Ans: Volume of sphere $= \frac{4}{3} π r^{3}$ and radius $r = 4.9 cm$

$= \frac{4}{3} \times \frac{22}{7} \times 4.9 \times 4.9 \times 4.9 c m^{3}$

$= 493 c m^{3}$

Mass of $1 c m^{3}$ of metal is $7.8 g$

$Mass of the shot put = volume \times density$

$= 7.8 \times 493 g$

$= 3845.44 g = 3.85 kg$

34. The capacity of a hemispherical tank is $155.232 l .$ Find its radius.

Ans: Capacity of tank $=$ Its Volume $= \frac{2}{3} π r^{3}$

$\frac{2}{3} π r^{3} = 155.232 l$

$= 155.232 \times 1000 c m^{3}$

$= 155232 c m^{3}$

$\frac{2}{3} \times \frac{22}{7} \times r^{3} = 155232$ ,

$r^{3} = \frac{155232 \times 3 \times 7}{2 \times 22}$

$r^{3} = 3528 \times 3 \times 7$

$r^{3} = (2 \times 3 \times 7)^{3}$

$r = 2 \times 3 \times 7 = 42 cm$

Hence radius of tank $= 42 cm$

35. What length of tarpaulin $3 m$ wide will required to make conical tent of height $8 m$ and base radius $6 m$ ? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately $20 cm$

Ans: Here $h = 8 m$ and $r = 6 m$

$l = \sqrt{r^{2} + h^{2}} = \sqrt{36 + 64} = 10 m$

Curved surface area $= π r l$

$= 3.14 \times 6 \times 10 = 188.4 m^{2}$

Length of tarpaulin required $= \frac{area}{width} = \frac{188.4}{3}$

$= 62.8 m$

Extra length required for wastage $= 20 cm = 0.2 m$

Hence, total length required $= 62.8 + 0.2$

$= 63 m$

36. A capsule of medicine is in the shape of a sphere of diameter $3.5 mm$ How much medicine $(in m m^{3})$ is needed to fill this capsule?

Ans: Given radius of capsule $= \frac{3.5}{2} mm$

$Amount of medicine = Volume of capsule = \frac{4}{3} π r^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times \frac{{(3.5)}^{3}}{2} m m^{3}$

$= \frac{4}{3} \times \frac{22}{7} \times \frac{3.5}{2} \times \frac{3.5}{2} \times \frac{3.5}{2}$

$= 22.46 m m^{3} (approx)$

37. A wall of length $10 m$ was to be built across an open ground. The height of wall is $4 m$ and thickness of the wall is $34 cm$ . If this wall is to be built up with bricks whose dimensions are $24 cm \times 12 cm \times 8 cm .$ How many bricks would be required

Ans: Length of wall $= 10 m = 1000 cm$

Thickness $= 24 cm$

Height $= 4 m = 400 cm$

Volume of wall $=$ length $\times$ thickness $\times$ height $= 1000 \times 24 \times 400 c m^{3}$

Now each brick is a cuboid with length $= 24 cm$

Breadth $= 12 cm$ and height $= 8 cm$

Volume of each brick $= 1 \times b \times h = 24 \times 12 \times 8 c m^{3}$

Number of bricks required $= \frac{volume of the wall}{volume of each brick}$

$= \frac{1000 \times 24 \times 400}{24 \times 12 \times 8} = 4166.6$

The wall requires $4167$ bricks.

38. The pillars of a temple are cylindrically shaped if each pillar has a circular base of radius $20 cm$ and height $10 m$ . How much concrete mixture would be required to build $14$ such pillars?

Ans: Radius of base of cylinder $= 20 cm$

Height of pillar $= 10 m = 1000 cm$

Volume of each cylinder $= π r^{2} h$

$= \frac{22}{7} \times 20 \times 20 \times 1000 c m^{3}$

$= \frac{8800000}{7} c m^{3}$

$= \frac{8.8}{7} m^{3}$

$∴$ Volume of 14 pillars $=$ volume of each cylinder $\times 14$

$= \frac{8.8}{7} \times 14 c m^{3} = 17.6 m^{3}$

So, $14$ pillars would need $17.6 m^{3}$ of concrete mixture.

39. A right triangle ABC with sides $5 cm, 12 cm$ , and $13 cm$ is revolved about the side $12 cm$ , find the volume of the solid so obtained

Ans: The solid obtained by revolving the given right triangle is a right circular cone with radius $= 5 cm$

And height $= 12 cm$

$∴$ Volume of solid $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} π \times 5^{2} \times 12 = 100 π c m^{3}$

40. The inner diameter of a circular well is $3.5 cm$ . It is $10 m$ deep find.

(i) Its inner curved surface area.

Ans: Given Inner diameter of well $= 3.5 m$

$∴$ Inner radius $= \frac{3.5}{2} = \frac{7}{4} m$

$r = \frac{7}{4} m$ and depth $h = 10 m$

(i) $∴$ Inner surface area $= 2 π r h$

$= (2 \times \frac{22}{7} \times 1.75 \times 10) m^{2}$

$= (2 \times \frac{22}{7} \times \frac{175}{100} \times 10) m^{2}$

$= (2 \times 22 \times \frac{25}{10}) m^{2}$

$= 110 m^{2}$

(ii) the cost of plastering this curved surface at the rate of Rs 40 per

Ans: The cost of plastering is Rs 40 per $m^{2}$

$∴$ Cost of plastering this surface area $= R s 40 \times 110$

$= R s 4400$

41. A Godown measures $40 m \times 25 m \times 10 m$ . Find the maximum number of wooden crates each measuring $10 m \times 1.25 m \times 0.5 m$ that can be stored in the go down

Ans: Dimensions of Godown

$= 40 m \times 25 m \times 10 m$

Volume of Godown $= 40 m \times 25 m \times 10 m = 10000 m^{3}$

volume of wooden carts $= 10 m \times 1.25 m \times 0.5 m = 6.25 m^{3}$

No. of wooden crates $= \frac{10, 000}{6.25}$

$= 800$

Hence, $800$ wooden crates are required.

42. The volume of a right circular cylinder is $576 π c m^{3}$ and radius of its base is $8 cm$ . Find the total surface area of the cylinder.

Ans: Volume of cylinder $= 576 π c m^{3}$

$r = 8 cm$

Volume of cylinder $= π r^{2} h$

$π r^{2} h = 576 π$

$h = \frac{576}{r^{2}} = \frac{576}{8^{2}} = 9$

$H = 9 cm$

$∴$ Total surface area $= 2 π r (r + h)$

$= 2 \times \frac{22}{7} \times (8 + 9) c m^{2}$

$= \frac{16 \times 22 \times 17}{7} c m^{2}$

$= 854.989 cm$

4 Marks Questions:

1. Shanti Sweets Stall was placing an order for making cardboard boxes for packing

their sweets. Two sizes of boxes were required. The bigger of dimensions $25 cm$ by $20$

$cm$ by $5 cm$ and the smaller of dimensions $15 cm$ by $12 cm$ by $5 cm . 5 %$ of the total

surface area is required extra, for all the overlaps. If the cost of the cardboard is $Rs . 4$

for $1000 c m^{2}$ , find the cost of cardboard required for supplying $250$ boxes of each kind.

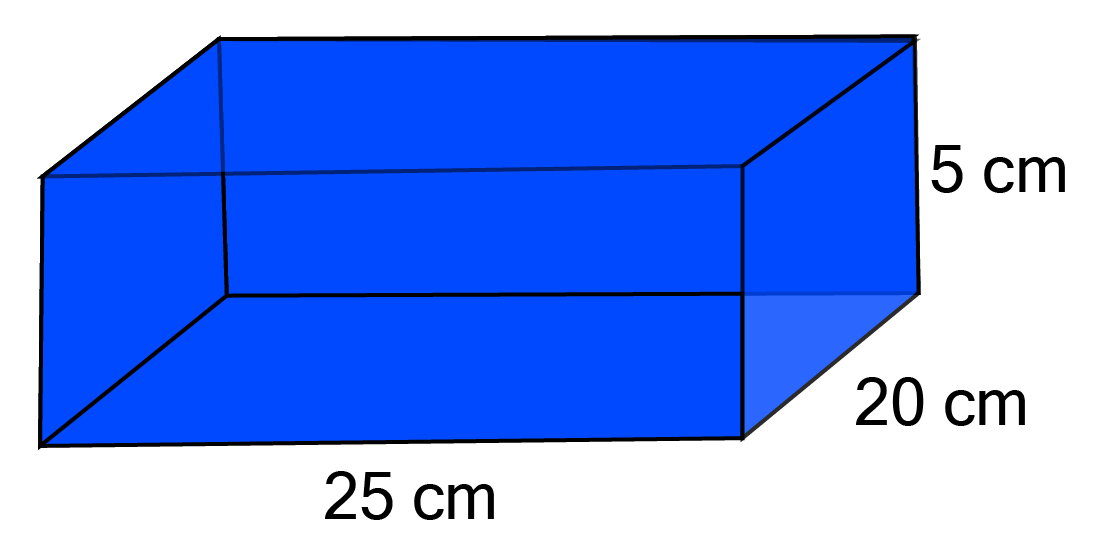
Ans: Given, Length of bigger cardboard box $(L) = 25 cm$

Breadth $(B)$ $= 20 cm$ and Height $(H) = 5 cm$

Total surface area of bigger cardboard box

$= 2 (LB + BH + HL)$

Substitute values

$= 2 (25 \times 20 + 20 \times 5 + 5 \times 25)$

$= 2 (500 + 100 + 125)$

$= 1450 c m^{2}$

$5 %$ extra surface of total surface area is required for all the overlaps.

$\Rightarrow 5 % of 1450 = \frac{5}{100} \times 1450 = 72.5 c m^{2}$

Now, total surface area of bigger cardboard box with extra overlaps

$= 1450 + 72.5 = 1522.5 c m^{2}$

$\Rightarrow$ Total surface area with extra overlaps of $250$ such boxes

$= 250 \times 1522.5 = 380625 c m^{2}$

Since, Cost of the cardboard for $1000 c m^{2} =$ Rs. $4$

Now, Cost of the cardboard for $1 c m^{2} =$ Rs. $\frac{4}{1000}$

Cost of the cardboard for $380625 c m^{2} =$ Rs. $\frac{4}{1000} \times 380625 =$ Rs. $1522.50$

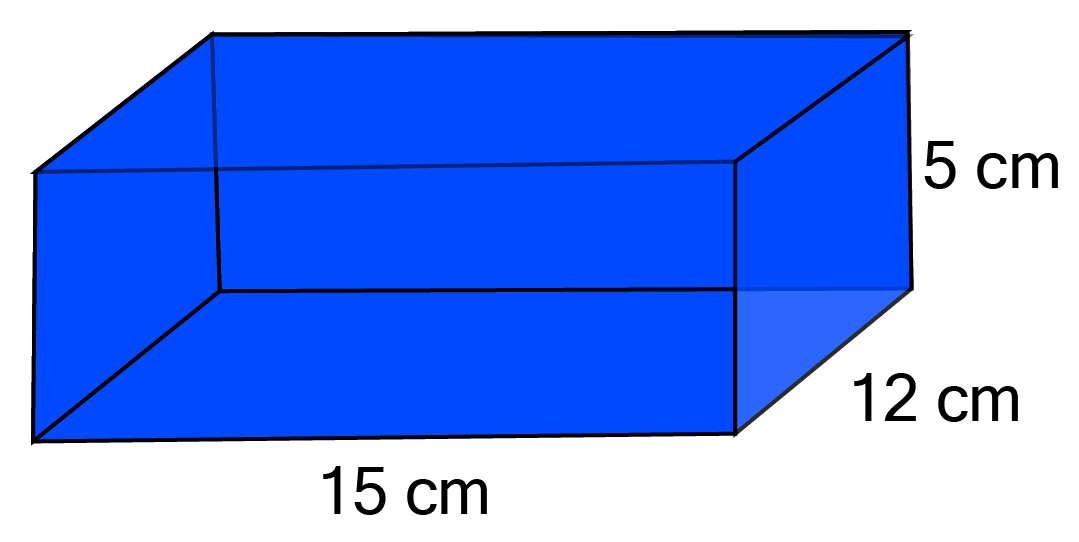
Now length of the smaller box $(l) = 15 cm$ ,

Breadth $(b) = 12 cm$ and Height $(h) = 5 cm$

Total surface area of the smaller cardboard box

$= 2 (l b + b h + h l)$

Substitute values

$= 2 (15 \times 12 + 12 \times 5 + 5 \times 15)$

$= 2 (180 + 60 + 75)$

$= 2 \times 315 = 630 c m^{2}$

$5 %$ of extra surface of total surface area is required for all the overlaps.

Thus, $5 % of 630 = \frac{5}{100} \times 630 = 31.5 c m^{2}$

Total surface area with extra overlaps $= 630 + 31.5 = 661.5 c m^{2}$

Now Total surface area with extra overlaps of $250$ such smaller boxes

$= 661.5 \times 250 = 165375 c m^{2}$

Cost of the cardboard for $1000 c m^{2} =$ Rs. $4$

Cost of the cardboard for $1 c m^{2} =$ Rs. $\frac{4}{1000}$

Cost of the cardboard for $165375 c m^{2} =$ Rs. $\frac{4}{1000} \times 165375 =$ Rs. $661.50$

Therefore, Total cost of the cardboard required for supplying $250$ boxes of each kind

$=$ Total cost of bigger boxes $+$ Total cost of smaller boxes

$=$ Rs. $1522.50 +$ Rs. $661.50$

$=$ Rs. $2184$

2. Find

(i) the lateral or curved surface area of a petrol storage tank that is $4.2 m$ in diameter

and $4.5 m$ high.

Ans: Diameter of cylindrical petrol tank $= 4.2 m$

Thus, Radius of the cylindrical petrol tank $= \frac{4.2}{2} = 2.1 m$

And Height of the $tank = 4.5 m$

Therefore, Curved surface area of the cylindrical tank $= 2 π r h = 2 \times \frac{22}{7} \times 2.1 \times 1.45 = 59.4 m^{2}$

(ii) how much steel was actually used if $\frac{1}{12}$ of the steel actually used was wasted in making the tank?

Ans: Let the actual area of steel used be $x$ meters

Since $\frac{1}{12}$ of the actual steel used was wasted, the area of steel which has gone into the tank.

$x - \frac{1}{12} x = \frac{11}{12} x$

$\frac{11}{12} x = 59.4$

$\Rightarrow x = 59.4 \times \frac{12}{11} = 64.8 m^{2}$

Hence, the steel actually used is $64.8 m^{2}$ .

3. A hemispherical bowl made of brass has inner diameter $10.5 cm$ . Find the cost of

tinplating it on the inside at the rate of Rs. $16$ per $100 c m^{2}$ .

Ans: Inner diameter of bowl $= 10.5 cm$

Thus, Inner radius of bowl $(r) = \frac{10.5}{2} = 5.25 cm$

Now, Inner surface area of bowl $= 2 π r^{2}$

$= 2 \times \frac{22}{7} \times 5.25 \times 5.25$

$= 2 \times \frac{22}{7} \times \frac{21}{4} \times \frac{21}{4} = \frac{693}{4} c m^{2}$

$∵$ cost of tin-plating per $100 c m^{2} =$ Rs. $16$

Then, Cost of tin-plating per $1 c m^{2} = \frac{16}{100}$

Therefore, Cost of tin-plating per $\frac{693}{4} c m^{2} = \frac{16}{100} \times \frac{693}{4} =$ Rs. $27.72$

4. The diameter of the moon is approximately one fourth the diameter of the earth.

Find the ratio of their surface areas.

Ans: Let diameter of Earth $= x$

Thus, Radius of Earth $(r) = \frac{x}{2}$

Surface area of Earth $= 4 π r^{2} = 4 π \times \frac{x}{2} \times \frac{x}{2} = π x^{2}$

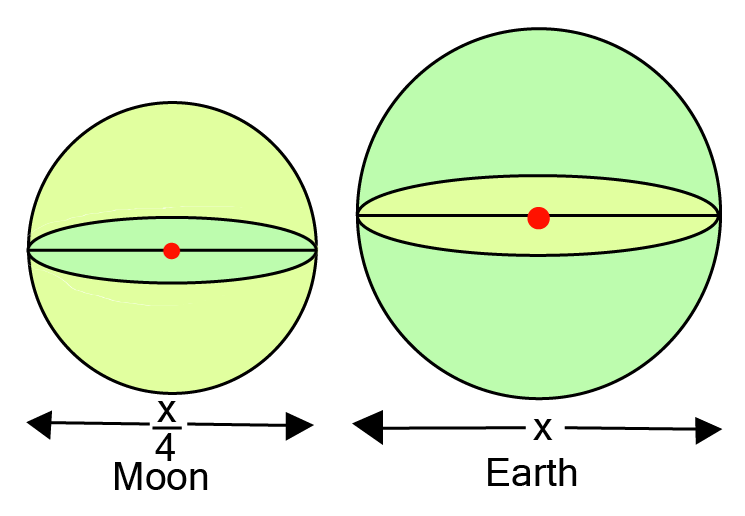
Now, Diameter of Moon $= \frac{1}{4} t h$ of diameter of Earth $= \frac{x}{4}$

Thus, Radius of $Moon (r) = \frac{x}{8}$

Surface area of Moon $= 4 π r^{2} = 4 π \times \frac{x}{8} \times \frac{x}{8} = \frac{π x^{2}}{16}$

Now, Ratio $= \frac{Surface area of Moon}{Surface area of Earth} = \frac{π x^{2}}{\frac{16}{π x^{2}}} = \frac{π x^{2}}{16} \times \frac{1}{π x^{2}} = \frac{1}{16}$

Therefore, Required ratio $= 1 : 16$

5. A solid cube of side $12 cm$ is cut into eight cubes of equal volume. What will be the

side of the new cube? Also, find the ratio between their surface areas.

Ans: Volume of solid cube $= (side)^{3} = (12)^{3} = 1728 c m^{3}$

Volume of each new cube $= \frac{1}{8}$ (Volume of original cube)

$= \frac{1}{8} \times 1728 = 216 c m^{3}$

Side of new cube $= \sqrt[3]{216} = 6 cm$

Now, Surface area of original solid cube $= 6 (side)^{2}$

$= 6 \times 12 \times 12 = 864 c m^{2}$

Now, Surface area of original solid cube $= 6$ (side) $^{2}$

$= 6 \times 6 \times 6 = 216 c m^{3}$

Now according to the question,

$\frac{Surface area of original cube}{Surface area of new cube} = \frac{864}{216} = \frac{4}{1}$

Hence, required ration between surface area of original cube to that of new cube $= 4 : 1$ .

6. The volume of a right circular cone is $9856 c m^{3} .$ If the diameter of the base if $28 cm$ ,

find:

(i) Height of the cone

Ans: Diameter of cone $= 28 cm$

Radius of cone $= 14 cm$

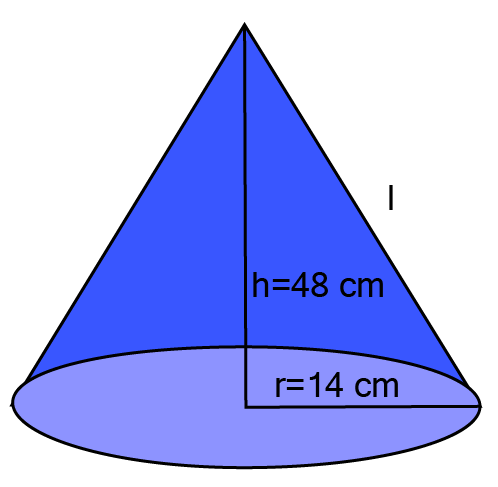
Volume of cone $= 9856 c m^{3}$

$\Rightarrow \frac{1}{3} π r^{2} h = 9856$

$\Rightarrow \frac{1}{3} \times \frac{22}{7} \times 14 \times 14 \times h = 9856$

$\Rightarrow h = \frac{9856 \times 3 \times 7}{22 \times 14 \times 14} = 48 cm$

(ii) Slant height of the cone

Ans: Slant height of cone $(l) = \sqrt{r^{2} + h^{2}}$

$= \sqrt{{(14)}^{2} + {(48)}^{2}} = \sqrt{196 + 2304}$

$= \sqrt{2500} = 50 cm$

(iii) Curved surface area of the cone.

Ans: Curved surface area of cone $= π r l$

$= \frac{22}{7} \times 14 \times 50 = 2200 c m^{2}$

7. The front compound wall of a house is decorated by wooden spheres of diameter

$21 cm$ , placed on small supports as shown in figure. Eight such spheres are used for

this purpose and are to be painted silver. Each support is a cylinder of radius $1.5 cm$

and height $7 cm$ and is to be painted black. Find he cost of paint required if silver paint

costs $25$ paise per $c m^{2}$ and black paint costs $5$ paise per $c m^{2}$

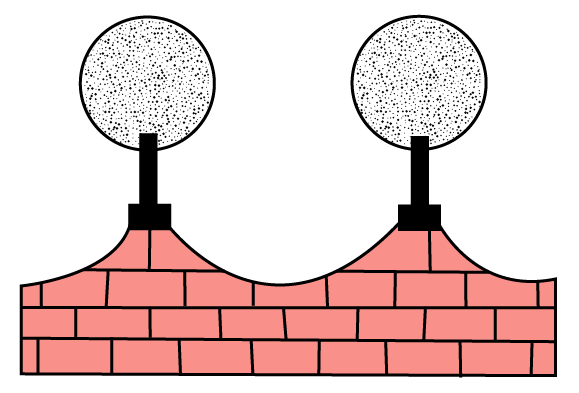
Ans: Diameter of a wooden sphere $= 21 cm$ .

Then, Radius of wooden sphere $(R) = \frac{21}{2} cm$

And Radius of the cylinder $(r) = 1.5 cm$

Surface area of silver painted part = Surface area of sphere - Upper part of cylinder for

support

$= 4 π R^{2} - π r^{2}$

$= π (4 R^{2} - r^{2})$

Substitute values

$= \frac{22}{7} \times [4 \times {(\frac{21}{2})}^{2} - {(\frac{15}{10})}^{2}]$

$= \frac{22}{7} \times [\frac{4 \times 441}{4} - \frac{9}{4}]$

$= \frac{22}{7} [\frac{1764 - 9}{4}]$

$= \frac{22}{7} \times \frac{1755}{4} = 1378.928 c m^{2}$

Surface area of such type of 8 spherical part $= 8 \times 1378.928$

$= 11031.424 c m^{2}$

Since, Cost of silver paint over $1 c m^{2} =$ Rs. $0.25$

Therefore, Cost of silver paint over $11031.928 c m^{2} = 0.25 \times 11031.928 =$ Rs. $2757.85$

Now, curved surface area of a cylindrical support $= 2 π r h$

$= 2 \times \frac{22}{7} \times \frac{15}{10} \times 7 = 66 c m^{2}$

Curved surface area of 8 such cylindrical supports $= 66 \times 8 = 528 c m^{2}$

Since, Cost of black paint over $1 c m^{2}$ of cylindrical support = Rs. $0.50$

Therefore, Cost of black paint over $528 c m^{2}$ of cylindrical support $= 0.50 \times 528$

$= Rs . 26.40$

Therefore, Total cost of paint required = Rs. $2757.85 +$ Rs. $26.4 = Rs .2784 .25$

8. The difference between outside and inside surface of a cylindrical metallic tripe $14$

$cm$ long is $44 sqcm$ . if the tripe is made of $99 c m^{3}$ . of metal, find the outer and inner

radius of the tripe.

Ans: Let $r_{1} cm$ and $r_{2} cm$ can be the inner and outer radii respectively of the pipe

Area of the outside surface $= 2 π r_{2} h$ sq unit

Area of the inside surface $= 2 π r_{1} h$ sq unit

By the given condition

$2 π r_{2} h - 2 π r_{1} h = 44$

or $2 π h (r_{2} - r_{1}) = 44$

$∴ 2 \times \frac{22}{7} \times 14 \times (r_{2} - r_{1}) = 44 (∵ h = 14 cm)$

Or, $88 (r_{2} - r_{1}) = 44$

$(r_{2} - r_{1}) = \frac{1}{2} \to (2)$

Again volume of the metal used in the pipe $= π (r_{2}^{2} - r_{1}^{2}) h$ cu units

$\frac{22}{7} (r_{2}^{2} - r_{1}^{2}) \times 14 = 99$

or, $44 (r_{2}^{2} - r_{1}^{2}) = \frac{99}{44} = \frac{9}{4} \to (2)$

Divide $(1) by (2)$

$\frac{(r_{2}^{2} - r_{1}^{2})}{r_{2} - r_{1}} = \frac{9}{4} \div \frac{1}{2}$

Or, $r \frac{(r_{2} - r_{1}) (r_{2} + r_{1})}{(r_{2} - r_{1})} = \frac{9}{4} \times \frac{2}{1}$ $∴ (r_{2} + r_{1}) = \frac{9}{2}$

Also, $(r_{2} - r_{1}) = \frac{1}{2} [$ From $(1)$ ]

$2 r_{2} = 5$

Adding

$r_{2} = \frac{5}{2}$

And, $\frac{5}{2} + r_{1} = \frac{9}{2}$

Therefore, $r_{1} = \frac{9}{2} - \frac{5}{2}$

Or, $r_{1} = 2$

Thus, outer radius $= 2.5 cm$ and inner radius $= 2 cm$ .

9. The ratio between the radius of the base and height of a cylinder is $2 : 3.$ Find the

total surface area of the cylinder if its volume is $1617 c m^{3}$

Ans: Let the radius of the base of the cylinder be $2 x cm$ .

Thus, Height of the cylinder $= 3 x cm$ .

Volume of the cylinder $= π r^{2} h$ cu units

$= \frac{22}{7} \times (2 x)^{2} \times 3 x cu cm .$

$= \frac{22}{7} \times 4 x^{2} \times 3 x cu cm .$

$= \frac{2647 x^{3}}{c m^{3}}$

By the given condition

$\frac{264}{7} x^{3} = 1617$

$x^{3} = \frac{1617 \times 7}{264} = \frac{49 \times 7}{8} = {(\frac{7}{2})}^{3}$

Thus, radius $= 2 \times \frac{7}{2} = 7 cm$

And height $= 3 \times \frac{7}{2} = \frac{21}{2} cm$

Total surface area $= 2 π r (r + h)$ sq units

$= 2 \times \frac{22}{7} \times 7 \times (7 + \frac{21}{2}) sq cm .$

$= 44 \times \frac{35}{2} sq cm$

$= 770 sq cm .$

Thus total surface area of the cylinder is $770 sq cm .$

10. Twenty-seven solid iron spheres, each of radius $r$ and surface area $S$ are melted to

form a sphere with surface area S' find the

(i) radius $r^{'}$ . of the new sphere

Ans: Total volume of $27$ iron spheres $=$ Volume of new sphere

Volume of each original sphere $= \frac{4}{3} π r^{3}$

Volume of $27$ spheres $= 27 \times \frac{4}{3} π r^{3} = \frac{108}{3} π r^{3}$

Volume of new sphere $= \frac{108}{3} π r^{3}$

$\frac{4}{3} π {(r^{'})}^{3} = \frac{108}{3} π r^{3}$

${(r^{'})}^{3} = \frac{108}{3} π r^{3} \times \frac{3}{4 π}$

$= 27 r^{3}$

Therefore, $r^{'} = 3 r$ .

(ii) ratio of $S$ and $S^{'}$

Ans: Surface area of original sphere $(S) = 4 π r^{2}$

Surface area of new sphere $(S^{'}) = 4 π {(r^{'})}^{2}$

$= 4 π (3 r)^{2}$

$= 36 π r^{2}$

Therefore, Ratio of $S$ and $S^{'} = \frac{4 π r^{2}}{36 π r^{2}} = \frac{1}{9} = 1 : 9.$

11. Shanti sweets stall was placing an order for making cardboard boxes for packing

their sweets two sizes of boxes were required. The bigger of dimensions and the

smaller of dimensions $15 cm \times 12 cm \times 5 cm$ for all the overlaps, $5 %$ of the total surface

area is required extra. If the cost of cardboard is Rs $4$ for $1000 c m^{2}$ . Find the cost of

cardboard required for supplying $250$ boxes of each kind.

Ans: Given dimensions of bigger box

$= 25 cm \times 20 cm \times 5 cm$

Total surface area of bigger box

$= 2 [25 \times 20 + 20 \times 5 + 25 \times 5] c m^{2}$

$= 2 [500 + 100 + 125] c m^{2} = 2 \times 725 = 1450 c m^{2}$

Extra cardboard for packing $= 5 %$ of $1450 c m^{2}$

$= \frac{5}{100} \times 1450 = 72.5 c m^{2}$

Cardboard used for making box $= 1450 + 72.5 = 1522.5 c m^{2}$

Dimensions of smaller box $= 15 cm \times 12 cm \times 5 cm$

Total surface area of smaller box $= 2 [15 \times 12 + 12 \times 15 + 15 \times 5] c m^{2}$

$= 2 [180 + 60 + 75] c m^{2}$

$= 2 \times 315 c m^{2} = 630 c m^{2}$

Extra cardboard for packing $= 5 %$ of $630$

$= \frac{5}{100} \times 630 = 31.5 c m^{2}$

Total area of cardboard $= 630 + 31.5 = 661.5 c m^{2}$

Total cardboard used for making $2$ boxes

$= (1522.5 + 661.5) c m^{2} = 2184 c m^{2}$

Cardboard used for making $250$ boxes $= 250 \times 2184 = 546000 c m^{2}$

Cost of cardboard $= \frac{4}{1000} \times 546000 = Rs .2184$

12. A hollow spherical shell is made of a metal of density $9.6 g / c m^{3}$ . The external

diameter of the shell is $10 cm$ and its internal diameter is $9 cm$ . Find

(i) Volume of the metal contained in the shell

Ans: External diameter of the spherical shell= $10 cm$

External radius $R = 5 cm$

Internal diameter $= 9 cm$

Internal radius $= \frac{9}{2} cm$ $r = \frac{9}{2} cm$

Volume of the metal $= \frac{4}{3} π [R^{3} - r^{3}] c m^{3}$

Substitute values

$= \frac{4}{3} π [5^{3} - {(\frac{9}{2})}^{3}] c m^{3}$

$= \frac{4}{3} \times \frac{22}{7} [125 - \frac{729}{8}] c m^{3}$

$= \frac{88}{21} \times \frac{271}{8} c m^{3} = 141.95 c m^{3}$

(ii) Weight of the shell.

Ans: Weight of the shell = Volume $\times$ Density

$= 141.95 c m^{3} \times 9.6 gm / c m^{3}$

$= 1363 gm$

$= 1.363 kg$

(iii) Outer surface area of the shell.

Ans: Outer surface area $= 4 π r^{2}$

$= 4 π (5)^{2}$

$= 4 \times \frac{22}{7} \times 25$

$= \frac{2200}{7} = 314.389 c m^{2}$

Topics Covered in Important Questions for Class 9 Maths Chapter 11

There are several topics which are covered in chapter 11, maths class 9 important questions. Given below, we have written down some of the important topics that students need to learn to answer the questions related to this chapter.

Cuboid

Students will be introduced to a new shape called cuboid in the surface area and volume class 9 important questions. A cuboid is a three-dimensional shape made by combining six rectangular faces, all of them being on the right angles. When it comes to finding out the cuboid's total surface area, it is the sum of the areas of all six sides with rectangular faces.

The cuboid's total surface area can be calculated by using the formula = 2(lb + bh + lh).

Lateral Surface Area of Cuboid

Lateral surface area is the sum of all the surface area of sides except the top and the bottom faces. The lateral surface area can be calculated by the following formula which is LSA (cuboid) = 2h(l + b)

Cube

A cube is just like a cuboid, but all the cube sides are of the same length. It is also a three-dimensional shape bounded by the six squares one at each of its face. The cube has 12 edges and a total of 8 vertices. The total surface area of the cube is written in the given formula with an explanation.

Total surface area(TSA) of the cube = 2(a × a + a × a + a × a)

TSA(cube) = 2 × (3a2) = 6a2.

Lateral Surface Area of The Cube

As we have already said earlier, it is the surface area of all the sides except the top and bottom. Thus, the cube's lateral surface area can be calculated by the following formula = 2(a × a + a × a) = 4a2.

Right Circular Cylinder

A right circular cylinder is said to be a cylinder with two parallel circular bases connected by a curved surface. In addition to this, these two bases are precisely aligned over each other, and their axis is at the right angles to the base.

The Curved Surface Area of A Right Circular Cylinder

To find out the cylinder's surface area, a student needs to get a cylinder with the base radius r and height h. When opened up along the diameter, the curved surface of a cylinder will have the diameter that is d = 2r of the circular base, and it will form a rectangle of a length 2πr with the height h. As a result, a cylinder's curved surface area with base radius r and height h will be 2π × r × h.

Total Surface Area of A Right Circular Cylinder

The cylinder's total surface area with the base (r) and height (h) = 2π × r × h + area of two circular bases.

TSA = 2π × r × h + 2 × πr2

TSA = 2πr(h + r)

Relationship Between The Slant Height And Height of A Right Circular Cone

With the Pythagoras theorem, we can find out the relationship between the slant height, which is denoted by (l), and height (h) of a right circular is l2= h2+r2.

Here r is the radius of the base of the given cone.

Surface Area and Volume Class 9 Important Questions for Exam Point of View

Now that we have cleared out the basics of chapter 11, it's time to give our students some questions to practice. You can find the solution to these questions if you have studied well and understood the topics correctly. Given below are a few questions which we would like you to attempt on your own and find out their answers.

Q1) How much of a chocolate ice-cream can be put into a single cone with the base radius of 3.5 cm and height 12 cm?

Q2) If we doubled the radius in a given cylinder and cut its height into half, then find out what will happen to its curved surface area?

Q3) The radii of two cylinders of the same height have the ratio 4:5 and then determine the ratio of their volumes for each other.

Q4) To make a closed cylindrical vessel of height 1 m and diameter 120 cm find out how much of the sheet is required to cover the cylinder vessel.

Q5) The curved surface area of a given ice-cream cone is 12 sq. cm, if the radius of its base is 4 cm, find out how much is the height of the cone?

Q6) A metallic sphere is said to be having the radius 5 cm. If the metal density is 7.5 g/cm2, find out the mass of the sphere (π = 22/7).

Q7) Find out the diameter of a cylinder with a height of 5 cm and the numerical value of its volume is equal to the numerical value of its curved surface area.

Q8) Calculate the paint required for the surface area of a hemispherical shaped dome of a temple with a radius of 14 m to be whitewashed from outside.

Q9) A right triangle XYZ with sides 10 cm, 24 cm and 26 cm is revolved around 10 cm. Find the volume of the solid so obtained. If it is now revolved around the side 24 cm, what would be the ratio of the two volumes of the two solids obtained for both cases?

Q10) Ishan provides water to his village, the village having a population of 5000 which requires 200 litres of water per head for each day. He has a storage tank with the measurements of 20 m × 15 m × 6 m. Find out for how many days the water present in his tank will last?

Tips to Learn Class 9 Maths Chapter 11 Surface Areas and Volumes

Before jumping into the formulas, make sure you know the basic shapes like cubes, cuboids, cylinders, and spheres. Visualizing them will make the calculations easier.
The key to mastering this chapter is memorizing and practising formulas like surface area and volume. Write them down and keep revising them until they become second nature.
Always draw a neat diagram of the solid you are working with. It helps you understand the dimensions and visualize the problem, making it easier to apply the right formula.
Relate the chapter to real-life objects like a juice can (cylinder) or a tennis ball (sphere). It will help you understand the practical application of the formulas.
Pay attention to the units of measurement in surface area and volume problems. Ensure that the units are consistent (like meters or centimetres) to avoid calculation errors.
Practice solving important questions from previous years. This will help you understand the types of problems asked and improve your speed and accuracy for exams.

Benefits of Class 9 Maths Chapter 11 Important Questions

It is not easy to prepare for the class 9th maths chapter 11 important question, but with Vedantu's solved question PDF, you can understand every concept more clearly and precisely. Given below, we have written some of the key benefits that the student receives when using our Pdf to find out the solution of an unsolved maths problem.

First, our teachers are experts in their subjects, so you find yourself to be stuck somewhere in your learning. Just open up the Pdf, and in a few minutes, all your doubts will be cleared.
Likewise, in mathematics, students need to perform a step by step solution for the given question. With the help of our solutions, students will know which steps are important and which ones they can skip while writing the answer thus, it will make things easier for the students in exams by saving their time.
In addition to this, a PDF can be opened anytime once it is downloaded offline. As a result, students can open up the Pdf straight from their hard drives or on their mobile devices without worrying about the internet connection.
Lastly, mathematics is one of the subjects where you need to practice more and more accurately with your answer and precise with your timing. With Vedantu's solved question, you will have more problems to solve for a given topic, increasing your confidence and helping you tackle multiple question types.

Conclusion

Vedantu’s Important Questions from Class 9 Maths Chapter 11 Surface Areas and Volumes is key to understanding how to calculate the areas and volumes of 3D shapes. With regular practice of these questions, you'll get a clear understanding of essential formulas and concepts. This chapter not only helps you solve problems accurately but also strengthens your foundation for future maths topics. So, focus on learning these important questions, apply the formulas, and practice solving different types of problems to improve your confidence and perform well in your exams!

Related Study Materials for Class 9 Maths Chapter 11 Surface Areas and Volumes

S.No	Study Materials for Class 9 Maths Chapter 11
1.	CBSE Class 9 Maths Surface Areas and Volumes Solutions
2.	CBSE Class 9 Maths Surface Areas and Volumes Notes
3.	CBSE Class 9 Maths Surface Areas and Volumes NCERT Exemplar
4.	CBSE Class 9 Maths Surface Areas and Volumes Important Formulas

CBSE Class 9 Maths Chapter-wise Important Questions

S.No	Chapter-wise Important Questions for Class 9 Maths
1.	Chapter 1 - Number Systems Questions
2.	Chapter 2 - Polynomials Questions
3.	Chapter 3 - Coordinate Geometry Questions
4.	Chapter 4 - Linear Equations in Two Variables Questions
5.	Chapter 5 - Introduction to Euclid’s Geometry Questions
6.	Chapter 6 - Lines and Angles Questions
7.	Chapter 7 - Triangles Questions
8.	Chapter 8 - Quadrilaterals Questions
9.	Chapter 9 - Circles Questions
10.	Chapter 10 - Heron’s Formula Questions
11.	Chapter 12 - Statistics Questions

FAQs on Surface Areas and Volumes Class 9 Important Questions: CBSE Maths Chapter 11

1. What are the important topics to study for CBSE Class 9 Chapter-13 Surface Areas and Volumes?

All important topics for CBSE Class 9 Chapter-13 Surface Areas and Volumes are available on Vedantu.

Here are some important topics to Study:

Cube
Cuboid
Right Circular Cylinder
Right Circular Cone
Sphere
Hemisphere
Hollow hemisphere.

2. The volumes of the two spheres are in the ratio 64:27. Find the ratio of their surface area.

The volume of the two spheres is in the ratio = $64 : 27$

We know that

Volume of sphere $= \frac{4}{3} π r^{3}$

Then,

$\frac{volume of the sphere(1)}{volume of the sphere(2)} = \frac{64}{27}$

$\Rightarrow \frac{\frac{4}{3} π r_{1}^{3}}{\frac{4}{3} π r_{2}^{3}} = \frac{64}{27}$

$\Rightarrow \frac{r_{1}^{3}}{r_{2}^{3}} = \frac{64}{27}$

$\Rightarrow \frac{r_{1}}{r_{2}} = \frac{4}{3}$

Then, the Ratio of areas in both spheres

$\frac{Area of the sphere(1)}{Area of the sphere(2)} = \frac{4 π r_{1}^{2}}{4 π r_{2}^{2}}$

$\Rightarrow \frac{Area of the sphere(1)}{Area of the sphere(2)} = \frac{r_{1}^{2}}{r_{2}^{2}}$

$\Rightarrow \frac{Area of the sphere(1)}{Area of the sphere(2)} = \frac{4^{2}}{3^{2}}$

$\Rightarrow \frac{Area of the sphere(1)}{Area of the sphere(2)} = \frac{16}{9}$

Hence, this is the answer.

3. The radius of the cylinder whose lateral surface area is 704 cm2 and height of 8 cm is:

Curved surface area of a cylinder of radius “R” and height “h” $= 2 π R h$

Hence, the Curved surface area of the cylinder

$2 \times \frac{22}{7} \times R \times 8 = 704$

$∴ R = 14 c m$

The radius of the base of the cylinder is 14 cm.

4. Where can I find the questions and formula for CBSE Class 9 chapter 11-Surface Areas and Volumes?

Surface Areas and Volumes is an important chapter for class 9 and it is highly visualized and practical in daily life. Complete organized questions and their detailed solutions are available on the Vedantu app. You can easily practice the previous year's questions and watch video lectures also.

5. If the edge of a cube is tripled, find the ratio of the surface areas of that of a volume of two cubes.

Let the edge of the cube be $x$

So, the surface area of the cube is $6 x^{2}$ and the volume will be $x^{3}$

Now, the edge of the cube is tripled that is $3 x$

So, the surface area will be $6 \times (3 x)^{2} = 54 x^{2}$ and volume will be $27 x^{3}$

Ratio of surface areas of both cubes $\frac{6 x^{2}}{54 x^{2}} = \frac{1}{9}$

Ratio of their volumes $\frac{x^{3}}{27 x^{3}} = \frac{1}{27}$

S.No	Study Materials for Class 9 Maths
1	CBSE Class 9 Maths NCERT Solutions
2	CBSE Class 9 Maths Important Questions
3	CBSE Class 9 Maths Sample Papers
4	CBSE Class 9 Maths RD Sharma Solutions
5	CBSE Class 9 Maths RS Aggarwal Solutions
6	CBSE Class 9 Maths Formulas
7	CBSE Class 9 Maths NCERT Exemplar Solutions
8	CBSE Class 9 Maths Revision Notes
9.	NCERT Class 9 Maths Book

Surface Areas and Volumes Class 9 Important Questions: CBSE Maths Chapter 11

CBSE Class 9 Maths Chapter 11 Important Questions - FREE PDF Download

Access Class 9 Maths Chapter 11: Surface Areas and Volumes Important Questions

Topics Covered in Important Questions for Class 9 Maths Chapter 11

Cuboid

Lateral Surface Area of Cuboid

Cube

Lateral Surface Area of The Cube

Right Circular Cylinder

The Curved Surface Area of A Right Circular Cylinder

Total Surface Area of A Right Circular Cylinder

Relationship Between The Slant Height And Height of A Right Circular Cone

Surface Area and Volume Class 9 Important Questions for Exam Point of View

Tips to Learn Class 9 Maths Chapter 11 Surface Areas and Volumes

Benefits of Class 9 Maths Chapter 11 Important Questions

Conclusion

Related Study Materials for Class 9 Maths Chapter 11 Surface Areas and Volumes

CBSE Class 9 Maths Chapter-wise Important Questions

Related Important Links for Maths Class 9

Vedantu Tatva Pro Question Bank Book CBSE Class 9 Mathematics Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 9 Year Long Recorded Course

Vedantu Tatva Pro CBSE Class 9 book set – Physics, Chemistry, Biology.

Vedantu Tatva Pro Question Bank Book CBSE Class 9 Set of 4 Books | Mathematics , Physics, Chemistry, Biology | Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 9 Year Long Recorded Course

Vedantu's Instasolve - 1 Month - 24 hours Unlimited Instant Doubt Solving

Vedantu's Instasolve - 12 Months - 24 hours Unlimited Instant Doubt Solving

Vedantu's Instasolve - 3 Months - 24 hours Unlimited Instant Doubt Solving

Biology - Vedantu - Round Neck T-Shirt

Doctor in the House - Men's Round Neck T-Shirt

Doctor in the House - Women's Round Neck T-Shirt

Dream Hustle Achieve - Women's Round Neck T-Shirt

Dream Hustle Achieve - Men's Hooded Sweatshirt

Dream Hustle Achieve - Women's Hooded Sweatshirt

FAQs on Surface Areas and Volumes Class 9 Important Questions: CBSE Maths Chapter 11