CBSE Class 9 Maths Important Questions - Chapter 7 Triangles

1 Marks Questions 

1. In fig, if AD =BC and $\angle $ BAD = $\angle $ ABC, then $\angle $ ACB is equal to

1. $\angle $ABD 

2. $\angle $ BAD 

3. $\angle $BAC 

4. $\angle $BDA 

Ans: ${\text{in}} \vartriangle ABC and \vartriangle ABD$ 

AD =BC      (given )

$\angle $ BAD = $\angle $ ABC    (Given) 

AB = AB   (Common side) 

$\therefore  \vartriangle ABC  \cong  \vartriangle ABD$

By CPCT theorem  $\angle ACB  =  \angle BDA$         ( By SAS Congruency )

Correct option is (D) $\angle $BDA

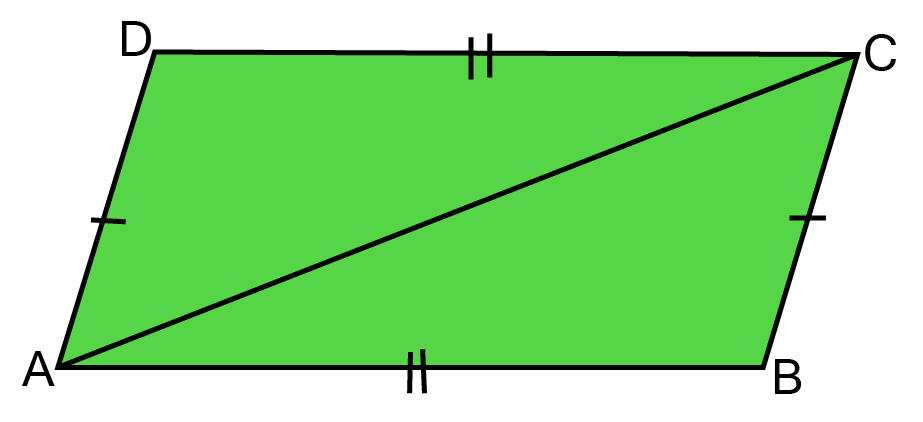
2. IN fig, if ABCD is a quadrilateral in which AD= CB, AB=CD, and $\angle $ D= $\angle $ B, then $\angle $CAB is equal to

1.  $\angle $ ACD 

2.  $\angle $ CAD

3.  $\angle $ ACD 

4.  $\angle $ BAD 

Ans: ${\text{in}} \vartriangle ABC and \vartriangle CDA$

CB = AD       (Given) 

AB=CD         (Given) 

$\angle $B = $\angle $D         (Given) 

$\therefore  \vartriangle ABC  \cong  \vartriangle CDA$       ( By SAS Congruency )

By CPCT theorem $ \angle CAB  =  \angle ACD$

Option (C) $\angle $ ACD is correct. 

3. If O is the mid – point of AB and $\angle $ BQO = $\angle $ APO, then $\angle $ OAP is equal to 

1.  $\angle $ QPA 

2.  $\angle $ OQB 

3.  $\angle $ QBO 

4.  $\angle $ BOQ 

Ans:

${\text{In}} \vartriangle {\text{AOP}} {\text{and}} \vartriangle BOQ$

$AO  =  BO   ..... {\text{(O}} {\text{is}} {\text{mid}}\,{\text{point}} {\text{of}} {\text{AB)}}$

$\angle APO  =   \angle BQO     {\text{(Given)}}  $

$\angle AOP  =   \angle BOQ     {\text{(Vertically opposite Angles)}}  $

$\therefore \vartriangle {\text{AOP}}  \cong  \vartriangle BOQ  $         ( By AAS Congruency )

${\text{By CPCT }} \angle OAP\, =  \angle QBO  $ 

Correct option is (C) $\angle $ QBO

4. IF AB$ \bot $BC and $\angle $ A = $\angle $ C, then the true statement is 

1. AB$ \ne $AC

2. AB=BC 

3. AB=AD 

4. AB=AC

  Ans:

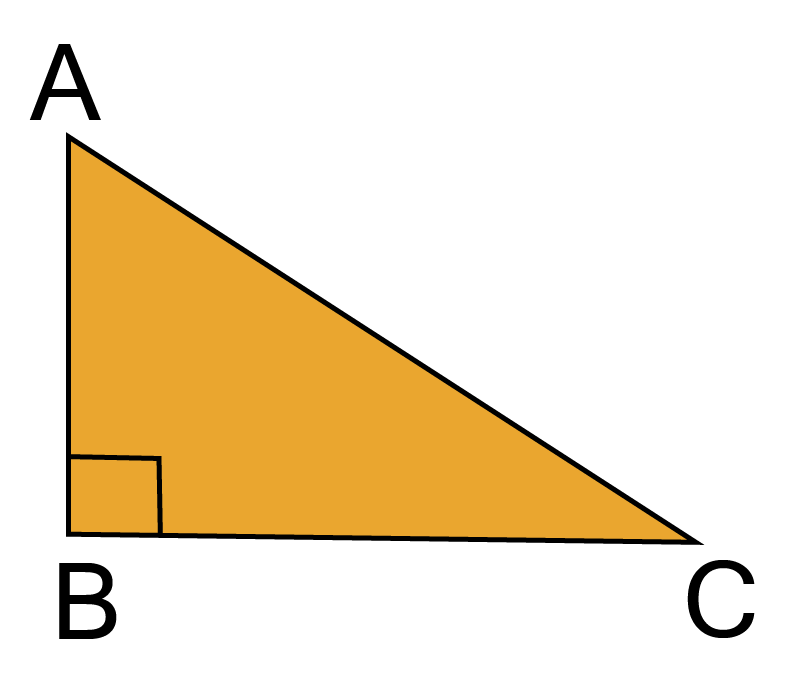
$\vartriangle ABC$

$\angle A  =  \angle C $

Sides opposite to equal angles are also equal

AB = BC

Correct option is  (B) AB=BC

5. If $\vartriangle $ABC is an isosceles triangle and $\angle $ B =${65^0}$  , find $\angle $ A. 

1. ${60^0}$ 

2. ${70^0}$ 

3. ${50^0}$ 

4.  none of these

Ans:

Since $\triangle \mathrm{ABC}$ is on isosceles triangle

$\therefore \angle \mathrm{B}=\angle \mathrm{C}$

$\therefore \angle \mathrm{B}=65^{\circ}$

$\therefore \angle \mathrm{C}=65^{\circ}$

$\therefore \angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ}$

$\therefore \angle \mathrm{A}+130^{\circ}=180^{\circ}$

$\therefore \angle \mathrm{A}=180^{\circ}-130^{\circ}$

$\therefore \angle \mathrm{A}=50^{\circ}$

Correct option is (c)${50^0}$

6. If AB=AC and $\angle $ ACD=${120^0}$ , find $\angle $A 

1. ${50^0}$ 

2. ${60^0}$ 

3. ${70^0}$

4. none of these 

Ans: 

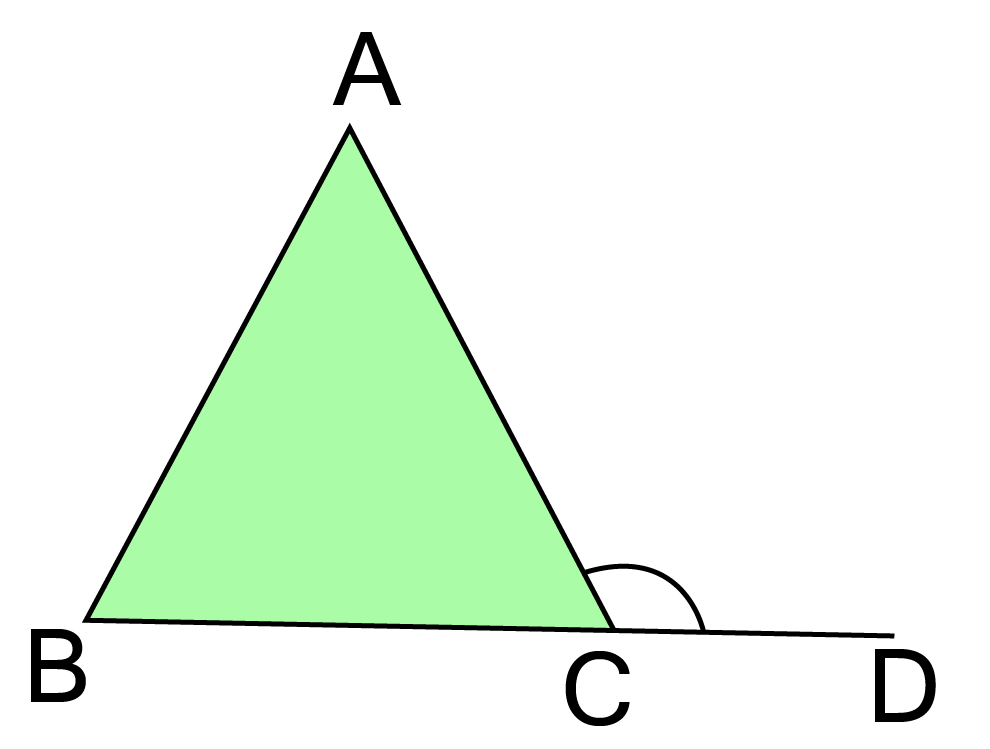
$\because {\text{AB}} = {\text{AC}}  $

$\Rightarrow \angle {\text{ABC}} = \angle {\text{ACB}} = {\text{x}}({\text{say)}}  $

${\text{Let}} \angle {\text{BAC}} = {\text{y}}  $ 

We know,

Exterior angles = sum of interior opposite angles

${120^\circ } = \angle {\text{ABC}} + \angle {\text{BAC}}  $

${120^\circ } = {\text{x}} + {\text{y}} -  -  - (1)  $

${\text{Again,}} \angle {\text{ACB}} + \angle {\text{ACD}} = {180^\circ }  $

${\text{x}} + {120^\circ } = {180^\circ }  $

$\therefore {\text{x}} = {60^\circ }  $

${\text{From(1),}}  $

${60^\circ } + {\text{y}} = {120^\circ }  $

$\Rightarrow {\text{y}} = {60^\circ }  $

$\Rightarrow \angle {\text{A}} = {60^\circ }  $ 

Correct option is  (b) ${60^0}$

7. What is the sum of the angles of a quadrilateral? 

1. ${260^0}$ 

2. ${360^0}$ 

3.  ${180^0}$ 

4.  ${90^0}$ 

  Ans: (b)${360^0}$

8. The sum of the angles of a triangle will be:

1. ${360^0}$ 

2. ${270^0}$  

3. ${180^0}$ 

4. ${90^0}$ 

 Ans: (c)${180^0}$

9. An angle is ${14^0}$ more than its complement. Find its measure.

1. 42 

2. 32 

3. 52 

4. 62 

Ans:  Two angles having sum equals to 90 degrees are called complementary angles.

let first angle = $x$

it’s Complement = ${90^ \circ } - \,x$

${\text{A}}{\text{.T}}{\text{.Q}}  $

$x  =  {14^ \circ } + {90^ \circ } - x  $

$x  =  104 - x  $

$\Rightarrow 2x  = {104^ \circ }  $

$\Rightarrow x  = \dfrac{{104}}{2}  $

$\therefore  x  =  {52^ \circ }  $ 

Correct option is (C) 52

10. An angle is 4 time its complement. Find measure.

1. 62 

2. 72 

3. 52 

4. 42 

Ans:

Two angles having sum equals to 90 degrees are called complementary angles.

let  angle = $x$

Therefore, it’s complement = ${90^ \circ } - x$

${\text{A}}{\text{.T}}{\text{.Q}}  $

$x = 4({90^ \circ } - x)  $

$x = \,{360^{ \circ  }}\, -  4x  $

$x + 4x  =  {360^{ \circ  }}  $

$\Rightarrow 5x = {360^{ \circ  }}  $

 $\Rightarrow x = \dfrac{{{{360}^{ \circ  }}}}{5}  $

 $\therefore x = {72^ \circ }  $ 

 Correct option (B) 72

11. Find the measure of angles which is equal to its supplementary. 

1. (A)${120^0}$ 

2. (B)${60^0}$  

3. (C) ${45^0}$ 

4. (D) ${90^0}$ 

Ans: Two angles having sum equals to 180 degrees are called supplementary angles.

$x  =  {180^ \circ } - x  $

$2x  =  {180^ \circ }  $

$\Rightarrow x  =  \dfrac{{{{180}^ \circ }}}{2}  $

$\therefore  x  = {90^ \circ }  $ 

Correct option is (D)${90^0}$

12. Which of the following pairs of angle are supplementary? 

1. ${30^0},{120^0}$ 

2. ${45^0},{135^0}$ 

3. ${120^0},{30^0}$ 

4. None of these. 

Ans: (B)${45^0},{135^0}$ 

Because ${45^ \circ } +  {135^ \circ }  =  {180^ \circ }$

13. Find the measure of each exterior angle of an equilateral triangle. 

1. ${110^0}$ 

2. ${100^0}$ 

3. ${120^0}$  

4. ${150^0}$  

Ans: (C)${120^0}$ 

Because ${180^ \circ }  -  {60^ \circ }  =  {120^ \circ }$

14. In an isosceles $\vartriangle $ ABC, if AB=AC and$\angle A = {90^0}$  , Find $\angle $ B. 

1.  ${45^0}$ 

2.  ${80^0}$ 

3. ${95^0}$ 

4. ${60^0}$  

Ans:  ${\text{AB}} {\text{ = }} {\text{AC}}  $

$\Rightarrow \angle C  =  \angle B  $     (angles opposite equal sides are also equal )

In  $\vartriangle ABC  $

$\angle A  +  \angle B\, + \,\angle C  =  {180^ \circ }  $ 

${90^ \circ }  +  2\angle B =  {180^ \circ }  $

$ \Rightarrow 2\angle B  =  {180^ \circ }  - {90^ \circ }  $

$\Rightarrow  \angle B  =  \dfrac{{{{90}^ \circ }}}{2}  $

$\Rightarrow  \angle B  =  {45^ \circ }  $ 

(A)${45^0}$ 

15. In a $\vartriangle $ABC, if $\angle $B= $\angle $C=${45^0}$  , Which is the longest side. 

1. BC 

2. AC 

3. CA

4. None of these. 

Ans: $\vartriangle ABC  $

  $\angle A  +  \angle B\, + \,\angle C  =  {180^ \circ }  $

  $\angle A  +  {45^ \circ }  +  {45^ \circ } = {180^ \circ }  $

  $\Rightarrow \angle A  =  {180^ \circ } - {90^ \circ }  =  {90^ \circ }  $ 

This is a right angles triangle in which right angle is at $\angle A$

Therefore, Side opposite to $\angle A$ is the longest side (hypotenuse) 

Correct option is (A) BC

16. In a $\vartriangle $ABC, if AB=AC and $\angle $ B=${70^0}$  , Find A. 

1.  ${40^0}$ 

2.  ${50^0}$ 

3.  ${45^0}$ 

4.  ${60^0}$ 

Ans: In $\vartriangle ABC  $

  $AB =  AC  $

  $\angle C = \angle B  =  {70^ \circ }  $

  $\angle A  +  \angle B\, + \,\angle C  =  {180^ \circ }  $

  $\angle A  +  {70^ \circ }  +  {70^ \circ } = {180^ \circ }  $

  $\Rightarrow \angle A  =  {180^ \circ } - {140^ \circ }  =  {40^ \circ }  $ 

Correct option is  (A)${40^0}$

17. Determine the shortest sides of the triangles. 

1. AC 

2. BC 

3. CA 

4. none of these 

 Ans: (B) BC

18. In an $\vartriangle $ABC, if $\angle A$ =${45^0}$  and $\angle B$ =${70^0}$  , determine the longest sides of the triangle. 

1. AC

2. AB 

3. BC 

4. none of these

Ans: 

Angle opposite to longest side is largest 

Side opposite to $\angle B$ is AC

Correct option is (a) AC

19. The sum of two angles of a triangle is equal to its third angle. Find the third angles. 

1. ${90^0}$ 

2. ${45^0}$  

3. ${60^0}$  

4.  ${70^0}$ 

  Ans: (a) ${90^0}$

20. Two angles of triangles are ${60^ \circ }, {70^ \circ }$respectively. Find third angles. 

1.  ${90^0}$ 

2.  ${45^0}$ 

3.  ${60^0}$ 

4.  ${50^0}$ 

 Ans: (d)${50^0}$

21. $\vartriangle $ABC is an isosceles triangle with AB=AC and $\angle B$ =${45^0}$  , find $\angle A$ . 

Ans: In $\vartriangle ABC  $

 $AB =  AC  $

 $\angle C = \angle B =  {45^ \circ }  $

 $\angle A  +  \angle B\, + \,\angle C  =  {180^ \circ }  $

 $\angle A  +  {45^ \circ }  +  {45^ \circ } = {180^ \circ }  $

 $\Rightarrow \angle A  =  {180^ \circ } - {90^ \circ }  =  {90^ \circ }  $ 

22. AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB (See figure)

Ans:  ${\text{In }}\vartriangle {\text{BOC and }}\vartriangle {\text{AOD}}  $

${\text{OBC  = OAD  = }}\left[ {{\text{Given}}} \right]  $

${\text{BOC  = AOD }}\left[ {{\text{Vertically Opposite angles}}} \right]  $

${\text{BC  =  AD }}\left[ {{\text{Given}}} \right]  $

${\text{BOC = AOD }}\left[ {{\text{By ASA congruency}}} \right]  $

${\text{OB  =  OA and OC  =  OD }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $ 

2 Marks Questions

1. In quadrilateral ABCD (See figure). AC = AD and AB bisects $\angle $A. Show that $\vartriangle $ABC$ \cong $  $\vartriangle $ABD. What can you say about BC and BD?

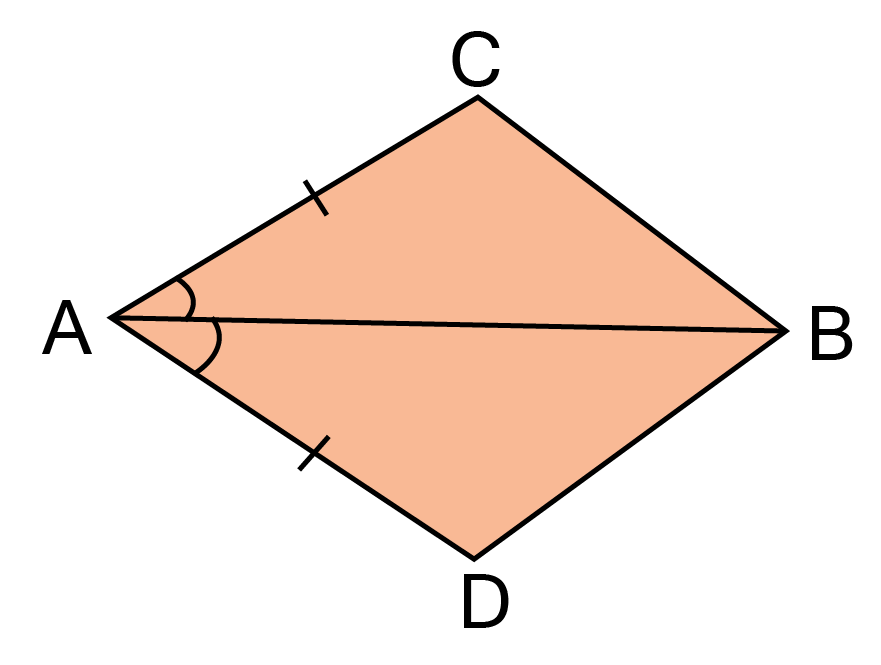
Ans: Given: In quadrilateral ${\text{ABCD}}$

$ {\text{AC  =  AD and AB bisects }}\angle {\text{A}}{\text{.}}  $

${\text{To prove:}}\vartriangle {\text{ABC }} \cong \vartriangle {\text{ABD}}$

  ${\text{Proof: In }}\vartriangle {\text{ABC and }}\vartriangle {\text{ABD,}}  $

  ${\text{AC  =  AD }}\left[ {{\text{Given}}} \right] $

  $\angle {\text{BAC   =  }}\angle {\text{BAD [ AB bisects }}\angle {\text{A]}}  $

  ${\text{AB  =  AB }}\left[ {{\text{Common}}} \right]  $

  $\vartriangle {\text{ABC}} \cong {\text{ }}\vartriangle {\text{ABD }}\left[ {{\text{By SAS congruency}}} \right]  $

  ${\text{Thus BC  =  BD }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $ 

2. ABCD is a quadrilateral in which AD = BC and $\angle $ DAB = $\angle $CBA. (See figure). Prove that: 

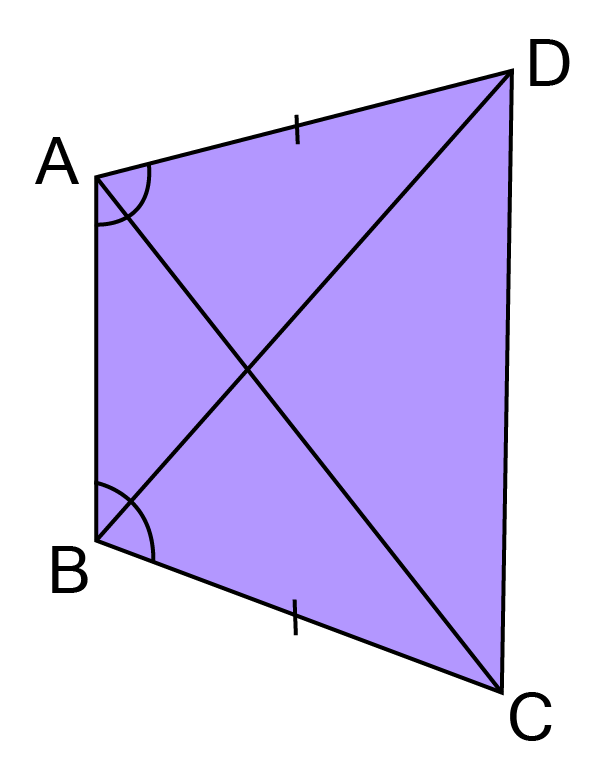
(i) $\vartriangle $ABD$ \cong $ $\vartriangle $BAC 

(i) $\vartriangle $ABD$ \cong $ $\vartriangle $BAC 

Ans: In $\text{ABC and ABD,}$

${\text{BC  =  AD }}\left[ {{\text{Given}}} \right] $

  ${\text{DAB  = CBA }}\left[ {{\text{Given}}} \right] $

  ${\text{AB  =  AB }}\left[ {{\text{Common}}} \right] $

  \[ABC\cong ABD\left[ \text{By SAS congruency} \right]\]

  x${\text{Thus AC  =  BD }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right] $. 

 (ii) BD = AC

Ans: Since $\vartriangle {\text{ABC }} \cong \vartriangle {\text{ABD}}$

${\text{AC  =  BD }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]$

(iii) $\angle $ ABD = $\angle $ BAC

 Ans: Since $\vartriangle {\text{ABC}} \cong {\text{ }}\vartriangle {\text{ABD}}$

$\angle {\text{ABD  = }}\angle {\text{BAC }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]$

3. l and m are two parallel lines intersected by another pair of parallel lines p and q (See figure). Show that $\vartriangle $ABC$ \cong $ $\vartriangle $CDA.

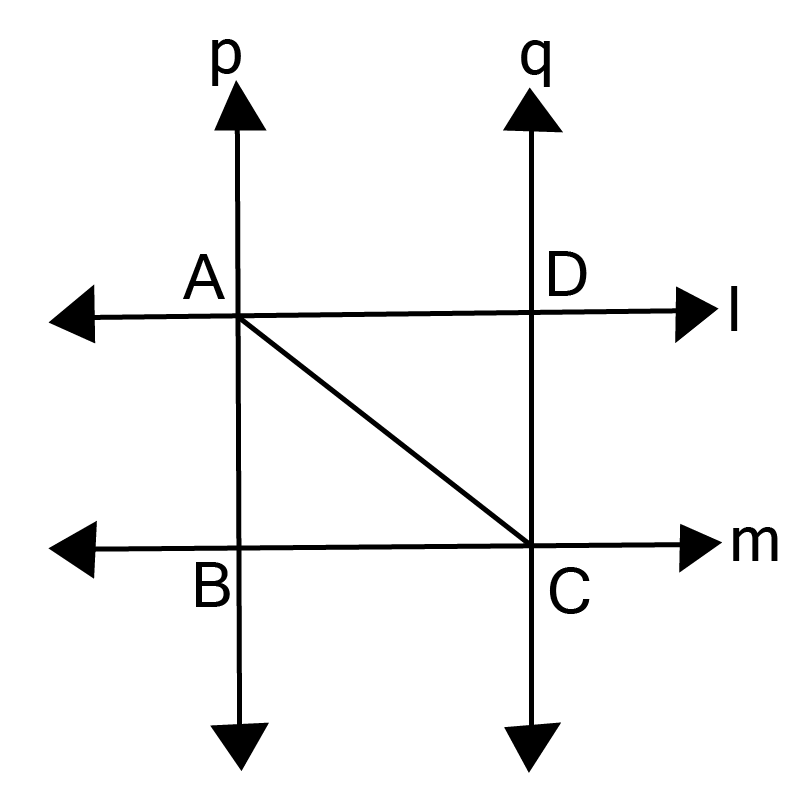
Ans:

AC being a transversal. [Given] 

${\text{Therefore }}\angle {\text{DAC  = }}\angle {\text{ACB }}\left[ {{\text{Alternate angles}}} \right]  $

${\text{Now p}}\parallel {\text{q }}\left[ {{\text{Given}}} \right]  $

  ${\text{And AC being a transversal}}{\text{. }}\left[ {{\text{Given}}} \right]  $

  ${\text{Therefore }}\angle {\text{BAC  = }}\angle {\text{ACD }}\left[ {{\text{Alternate angles}}} \right]  $

  ${\text{ Now In }}\vartriangle {\text{ABC and }}\vartriangle {\text{ADC,}}  $

  $\angle {\text{ACB  =  }}\angle {\text{DAC }}\left[ {{\text{Proved above}}} \right]  $

  $\angle {\text{BAC  = }}\angle {\text{ACD }}\left[ {{\text{Proved above}}} \right]  $

  ${\text{AC  =  AC }}\left[ {{\text{Common}}} \right]  $

  $\vartriangle {\text{ABC}} \cong {\text{ }}\vartriangle {\text{CDA }}\left[ {{\text{By ASA congruency}}} \right]  $ 

4. Line is the bisector of the angle A and B is any point on BP and BQ are perpendiculars from B to the arms of A. Show that:

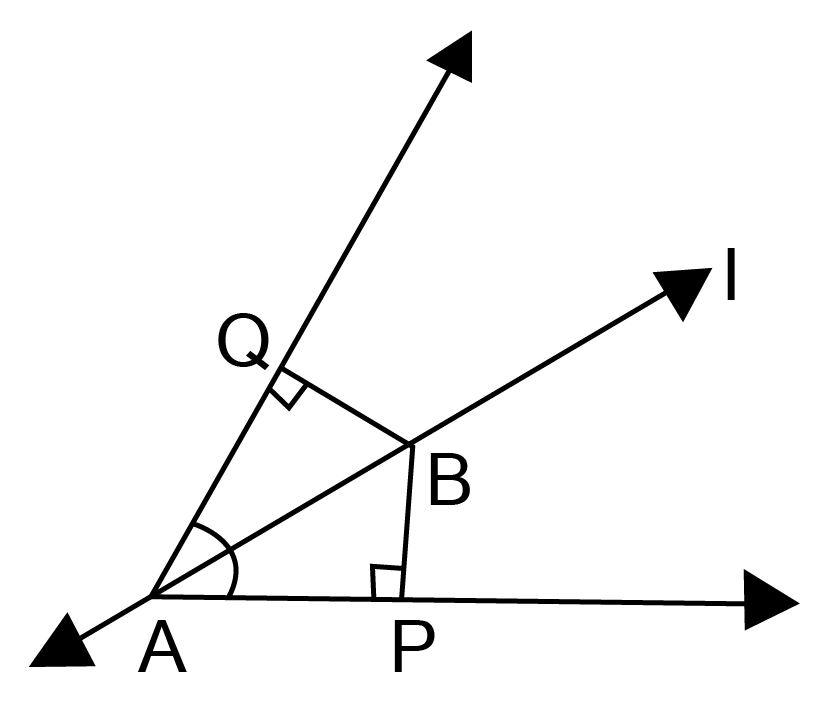
(i). $\vartriangle {\text{APB }} \cong {\text{ }}\vartriangle {\text{AQB}}$

Ans: ${\text{Given: Linel bisects }}\angle {\text{A}}$

$\angle {\text{BAP  = }}\angle {\text{BAQ}}  $

  ${\text{In }}\vartriangle {\text{ABP and }}\vartriangle {\text{ABQ}}  $

  $\angle {\text{BAP  = }}\angle {\text{BAQ}}\left[ {{\text{Given}}} \right]  $

  $\angle {\text{BPA  = }}\angle {\text{BQA  = }}\left[ {{\text{Given}}} \right]  $

  ${\text{AB  =  AB }}\left[ {{\text{Common}}} \right]  $

  $\vartriangle {\text{APB}} \cong {\text{ }}\vartriangle {\text{AQB }}\left[ {{\text{By ASA congruency}}} \right]  $ 

(ii). ${\text{BP  =  BQ}}$or ${\text{P}}$is equidistant from the arms of $\angle {\text{A }}$(see figure)

Ans: Since $\vartriangle {\text{APB}} \cong \,\vartriangle {\text{AQB}}$

${\text{BP  =  BQ }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $

${\text{B is equidistant from the arms of }}\angle {\text{A}}{\text{.}}  $ 

5. In figure, AC = AB, AB = AD and $\angle $ BAD = $\angle $ EAC. Show that BC = DE

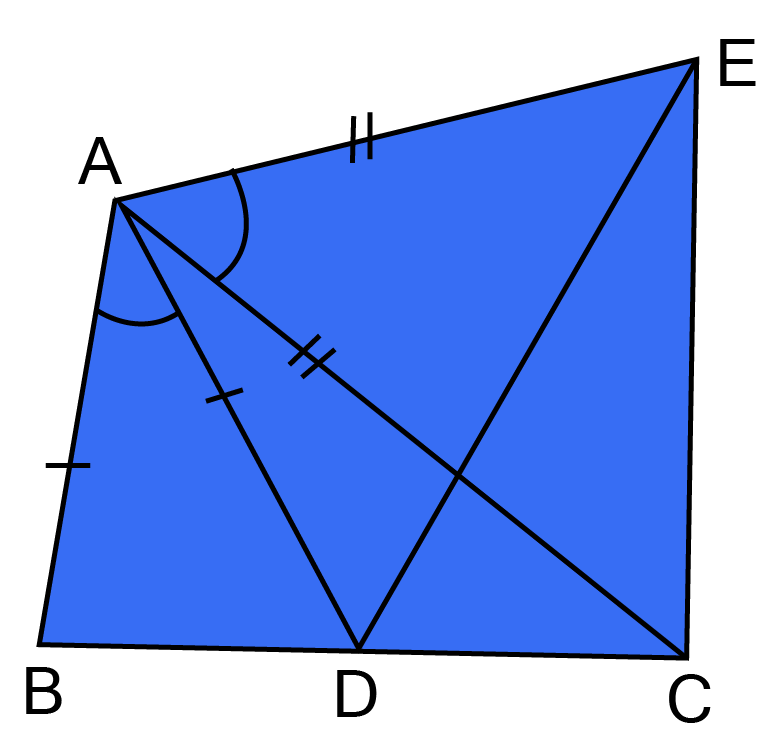
Ans: ${\text{Given that }}\angle {\text{BAD  =  }}\angle {\text{EAC}}$

${\text{Adding }}\angle {\text{DAC on both sides,}}  $

${\text{we get,}}\angle {\text{BAD  + }}\angle {\text{DAC  = }}\angle {\text{EAC  + }}\angle {\text{DAC}}  $ 

 ${\text{BAC  = EAD  }}{\text{..................}}\left( {\text{i}} \right)  $

  Now in $\vartriangle {\text{ABC}} and \vartriangle {\text{ADE }}  $

  ${\text{AB  =  AD }}\left[ {{\text{Given}}} \right]  $

  ${\text{ AC  =  AE }}\left[ {{\text{Given}}} \right]  $

  $\angle {\text{BAC  =  }}\angle {\text{DAE }}\left[ {{\text{From eq}}{\text{. }}\left( {\text{i}} \right)} \right]  $

  $\vartriangle {\text{ABC}} \cong {\text{ }}\vartriangle {\text{ADE }}\left[ {{\text{By SAS congruency}}} \right]  $

$  {\text{BC  =  DE }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $ 

6. AB is a line segment and P is the mid-point. D and E are points on the same side of AB such that BAD = ABE and EPA = DPB. Show that: (i) DAF FBPE D (ii) AD = BE (See figure)

Ans: ${\text{Given that }}\angle {\text{EPA  = }}\angle {\text{DPB}}$

${\text{Adding }}\angle {\text{EPD on both sides, we get,}}  $

$\angle {\text{EPA  + }}\angle {\text{EPD  = }}\angle {\text{DPB  + }}\angle {\text{EPD}}  $

$\angle {\text{APD  = }}\angle {\text{BPE  }}{\text{.............}}\left( {\text{i}} \right)  $

${\text{Now in}}\vartriangle {\text{APD and }}\vartriangle {\text{BPE,}}  $

$\angle {\text{PAD  = }}\angle {\text{PBE [}}\angle {\text{BAD  = }}\angle {\text{ABE }}\left( {{\text{given}}} \right){\text{]}}  $

$\angle {\text{PAD  = }}\angle {\text{PBE}}  $

${\text{ AP  =  PB }}\left[ {{\text{P is the mid - point of AB}}} \right]  $

$\angle {\text{APD  = }}\angle {\text{BPE }}\left[ {{\text{From eq}}{\text{. }}\left( {\text{i}} \right)} \right]  $

$\angle {\text{DPA = }}\angle {\text{EBP }}\left[ {{\text{By ASA congruency}}} \right]  $

${\text{AD  =  BE }}\left[ {{\text{ By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $ 

7. In an isosceles triangle ABC, with AB = AC, the bisectors of B and C intersect each other at O. Join A to O. Show that: 

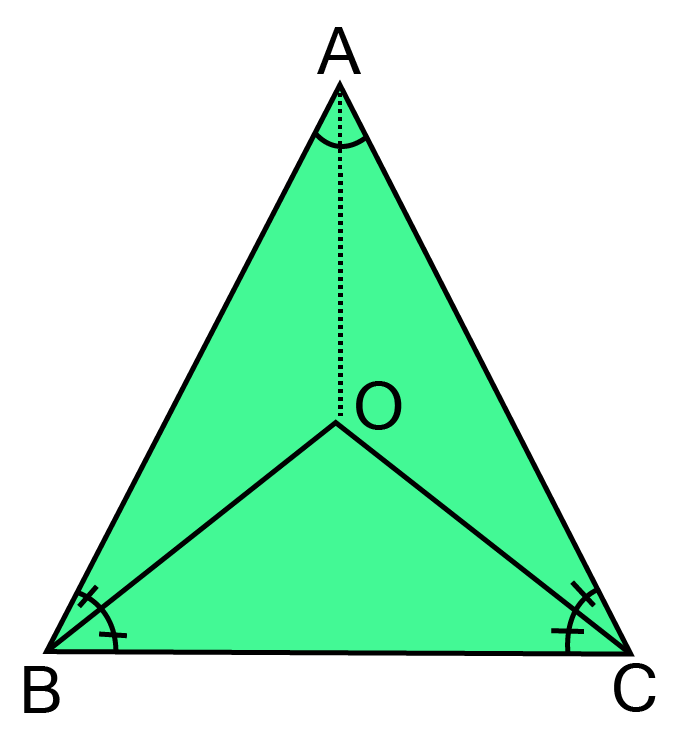
(i) OB = OC

Ans:  ${\text{ABC is an isosceles triangle in which}}$

${\text{AB  =  AC}}$

$\Rightarrow {\text{ C  =  B }}\left[ {{\text{Angles opposite to equal sides}}} \right]  $

$\vartriangle {\text{ OCA  + }}\vartriangle {\text{OCB  = }}\vartriangle {\text{OBA  + }}\vartriangle {\text{OBC}}  $

 ${\text{OB bisects }}\angle {\text{B and OC bisects }}\angle {\text{C }}  $

 $ \angle {\text{OBA  = }}\angle {\text{OBC and }}\angle {\text{OCA  =  }}\angle {\text{OCB}}  $

$\angle {\text{OCB  + }}\angle {\text{OCB  = }}\angle {\text{OBC  + }}\angle {\text{OBC}}  $

  $ {\text{2}}\angle {\text{OCB  =  2}}\angle {\text{OBC}}  $

  $\angle {\text{OCB  = }}\angle {\text{OBC}}  $

  ${\text{Now in }}\vartriangle {\text{OBC,}}  $

  $\angle {\text{OCB  = }}\angle {\text{OBC }}\left[ {{\text{Proved above}}} \right]  $

  ${\text{OB  =  OC }}\left[ {{\text{Sides opposite to equal sides}}} \right]  $ 

(ii) AO bisects A

Ans: In $\vartriangle {\text{AOB and }}\vartriangle {\text{AOC,}}$

${\text{AB  =  AC }}\left[ {{\text{Given}}} \right]  $

 $\angle {\text{OBA  = }}\angle {\text{OCA}}\left[ {{\text{Given}}} \right]  $

 ${\text{And }}\angle {\text{B  =  }}\angle {\text{C}}  $

  $\dfrac{1}{2}\angle {\text{B = }}\dfrac{1}{2}\angle {\text{C}}  $ 

  $\angle {\text{OBA  = }}\angle {\text{OCA}}  $

  ${\text{OB  =  OC }}\left[ {{\text{Proved above}}} \right]  $

  $\vartriangle {\text{AOB }} \cong \vartriangle {\text{AOC }}\left[ {{\text{By SAS congruency}}} \right]  $ 

8. In ABC, AD is the perpendicular bisector of BC (See figure). Show that ABC is an isosceles triangle in which AB = AC.

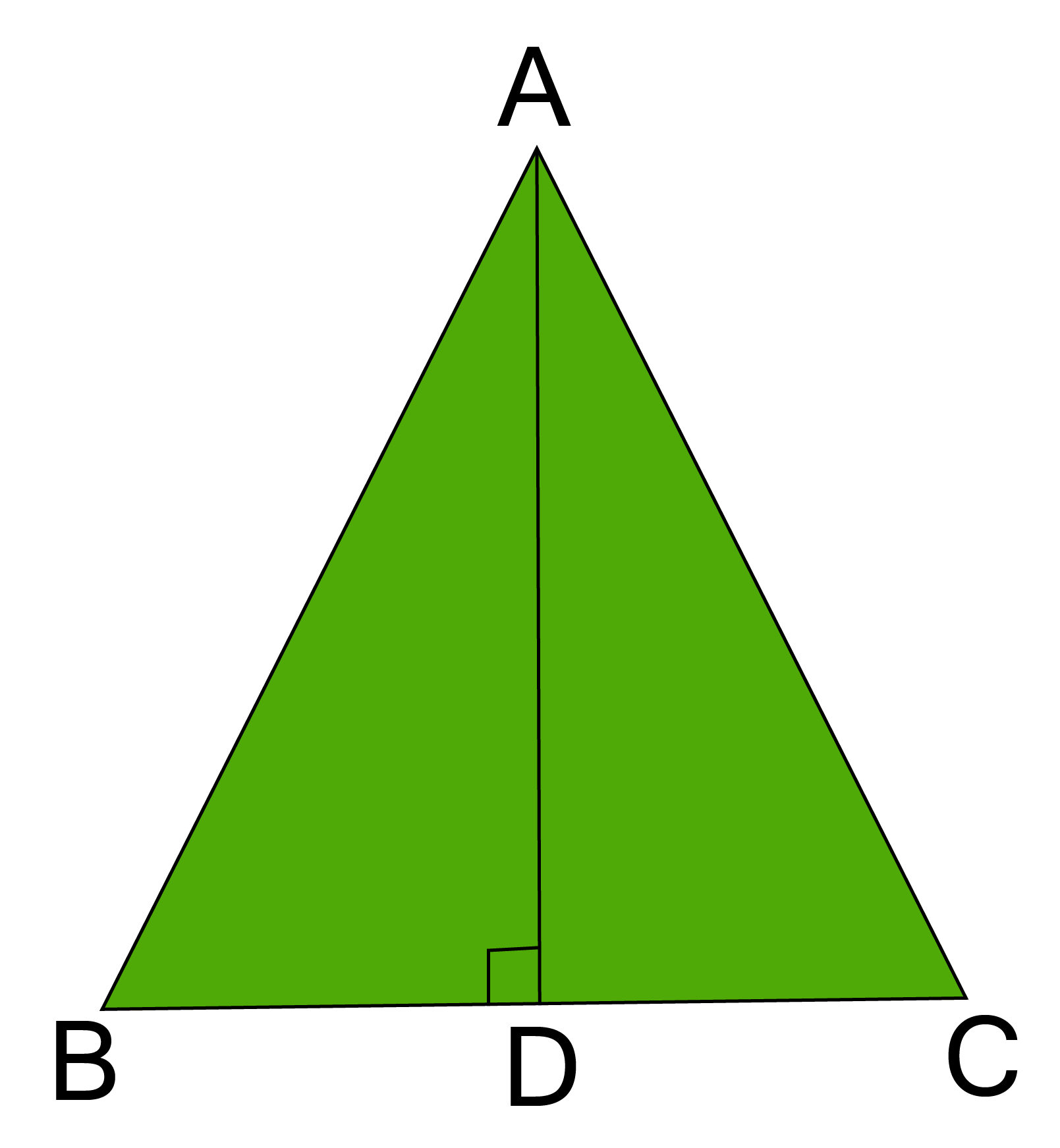
 Ans:  ${\text{In  }}\vartriangle {\text{AOB and }}\vartriangle {\text{AOC,}}$,

$ {\text{BD  =  CD }}\left[ {{\text{AD bisects BC}}} \right]  $

$ \angle {\text{ADB  = }}\angle {\text{ADC }}\left[ {{\text{[ Since AD }} = {\text{ BC}}} \right]  $

 $ {\text{AD  =  AD }}\left[ {{\text{Common}}} \right]  $

  $\therefore \vartriangle {\text{ABD }} \cong {\text{ }}\vartriangle {\text{ACD }}\left[ {{\text{By SAS congruency}}} \right]  $

 $ {\text{therefore, AB  =  AC }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $

 $ {\text{Therefore, ABC is an isosceles triangle}}{\text{.}}  $ 

9. ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See figure). Show that these altitudes are equal.

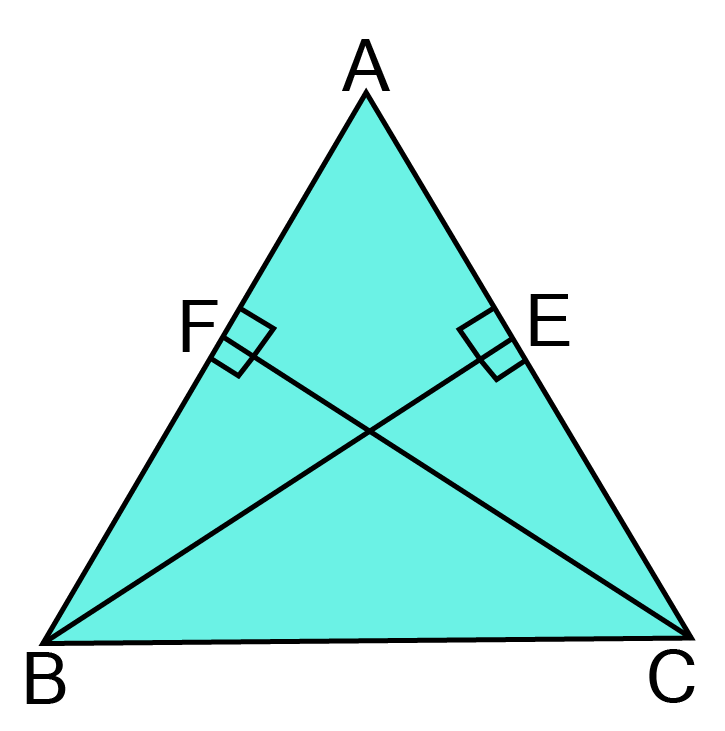
 Ans: In $\vartriangle {\text{ABE and }}\vartriangle {\text{ACF,}}$

$\angle {\text{A = }}\angle {\text{A }}\left[ {{\text{Common}}} \right]  $

$\angle {\text{AEB  = }} \angle {\text{AFC}} {\text{[ Since   AD}} \bot {\text{BC}}\left] {\text{ }} \right[{\text{Given]}} $

  ${\text{AB  =  AC }}\left[ {{\text{Given}}} \right]  $

  $\vartriangle {\text{ABE }} \cong  {\text{ }}\vartriangle {\text{ACF }}\left[ {{\text{By ASA congruency}}} \right]  $

${{\text{BE  =  CF }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]} $ 

${{\text{Altitudes are equal}}{\text{.}}} $

10. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (See figure). Show that: 

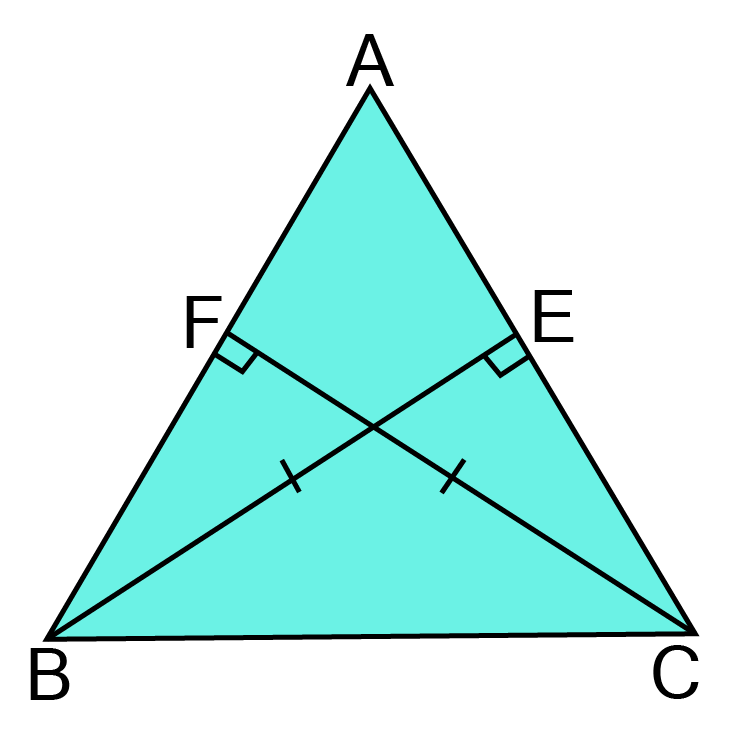
(i). In $\vartriangle {\text{ABE and }}\vartriangle {\text{ACF,}}$

Ans: In $\vartriangle {\text{ABE and }}\vartriangle {\text{ACF,}}$

$\angle {\text{A = }}\angle {\text{A }}\left[ {{\text{Common}}} \right]  $

$\angle {\text{AEB  = }}\angle {\text{AFC  = 9}}{{\text{0}}^0}\left[ {{\text{Given}}} \right]  $

${\text{BE  =  CF }}\left[ {{\text{Given}}} \right]  $

$\vartriangle {\text{ABE }} \cong {\text{ }}\vartriangle {\text{ACF }}\left[ {{\text{By ASA congruency}}} \right]  $

(ii) AB = AC or $\vartriangle $ABC is an isosceles triangle.

Ans: Since, $\vartriangle {\text{ABE }} \cong {\text{ }}\vartriangle {\text{ACF}}$

${\text{BE  =  CF }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $

$  \vartriangle {\text{ABC is an isosceles triangle}}{\text{.}}  $

11. ABC and DBC are two isosceles triangles on the same base BC (See figure). Show that $\angle $ABD = $\angle $ACD.

Ans: In isosceles triangle ABC

${\text{AB  =  AC }}\left[ {{\text{Given}}} \right]  $

$\angle {\text{ACB  = }}\angle {\text{ABC }}{\text{..........}}\left( {\text{i}} \right){\text{ }}\left[ {{\text{Angles opposite to equal sides}}} \right]  $

  ${\text{Also in Isosceles triangle BCD}}{\text{.}}  $

  ${\text{BD  =  DC}}  $

  $\angle {\text{BCD  = }}\angle {\text{CBD  }}{\text{...........}}\left( {{\text{ii}}} \right)\left[ {{\text{Angles opposite to equal sides}}} \right]  $

  ${\text{Adding eq}}{\text{. }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right) $

  $\angle {\text{ACB  + }}\angle {\text{BCD  = }}\angle {\text{ABC  + }}\angle {\text{CBD}}  $

  $\angle {\text{ACD  = }}\angle {\text{ABD or}}  $

  $\angle {\text{ABD  = }}\angle {\text{ACD}}  $ 

12. ABC is a right angled triangle in which $\angle {\text{A}}$ = ${90^0}$ and AB = AC. Find$\angle {\text{B and }}\angle {\text{C}}$.

Ans: $\vartriangle $ABC is a right triangle in which,

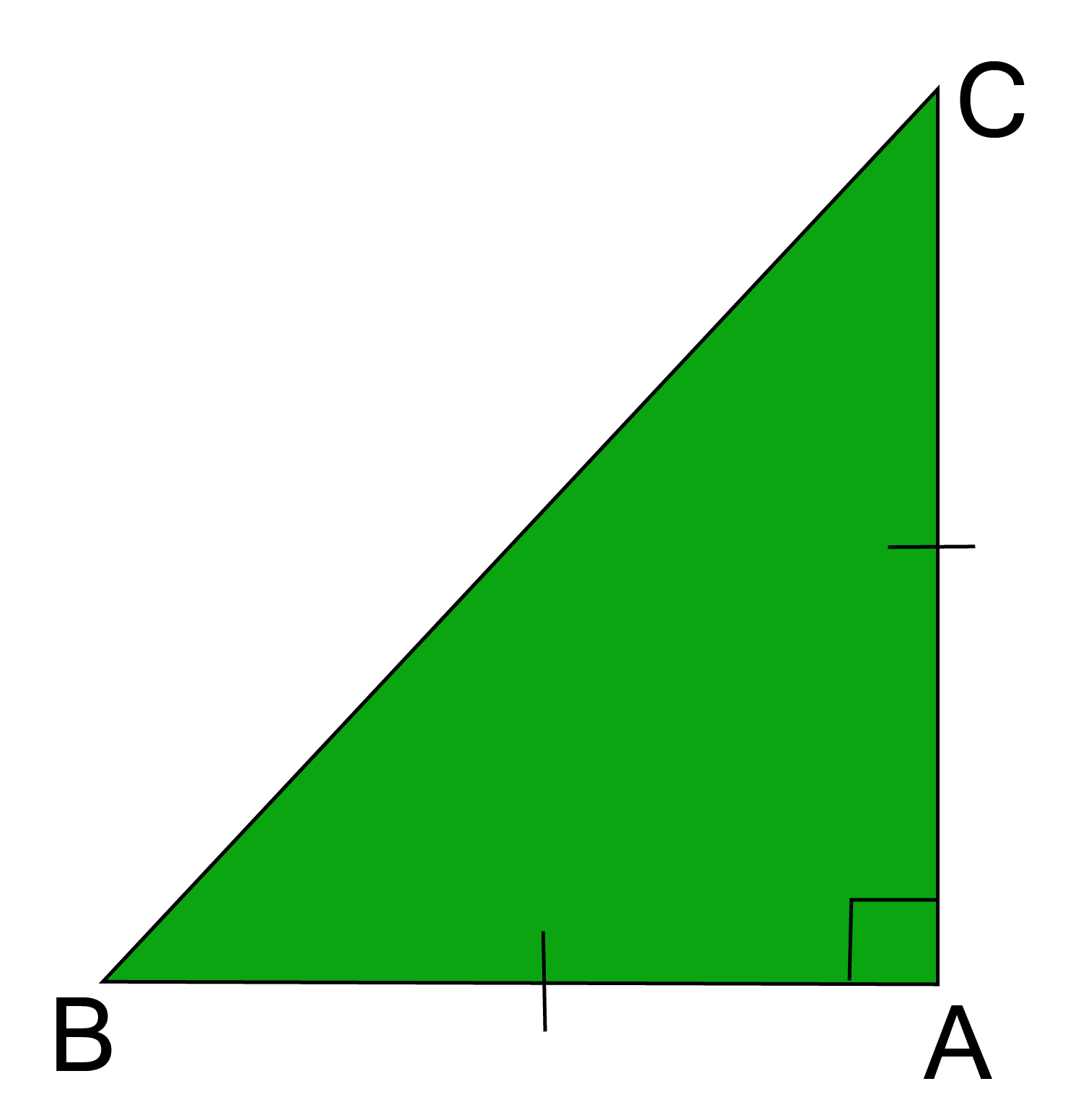
$\angle {\text{A  =  9}}{{\text{0}}^0}{\text{And AB  =  AC}}  $

${\text{In  }}\vartriangle {\text{ABC,}}  $

 ${\text{AB  =  AC }} \Rightarrow \angle {\text{C  =  }}\angle {\text{B }}{\text{............}}\left( {\text{i}} \right)  $

${\text{We know that,in  }}\vartriangle {\text{ABC, }}\angle {\text{A  +  }}\angle {\text{B  +  }}\angle {\text{C  =   18}}{{\text{0}}^0}\left[ {{\text{Angle sum property}}} \right]  $

${\text{9}}{{\text{0}}^0}{\text{  +  B  +  B  = 18}}{{\text{0}}^0}{\text{  [ }}\angle {\text{A  =  9}}{{\text{0}}^0}\left( {{\text{given}}} \right){\text{ and }}\angle {\text{B  = }}\angle {\text{C }}\left( {{\text{from eq}}{\text{. }}\left( {\text{i}} \right)} \right]  $

 ${\text{2 }}\angle {\text{B  =   9}}{{\text{0}}^0}  $

 $\angle {\text{B  =   9}}{{\text{0}}^0}{\text{Also }}\angle {\text{C  = 4}}{{\text{5}}^0}{\text{ [ }}\angle {\text{B  = }}\angle {\text{C]}}  $ 

13. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that: 

(i) AD bisects BC. 

Ans: In $\vartriangle {\text{ABD and }}\vartriangle {\text{ACD,}}$

${\text{AB  =  AC }}\left[ {{\text{Given}}} \right]  $

$\vartriangle {\text{ADB  =  }}\vartriangle {\text{ADC  = 9}}{{\text{0}}^0}{\text{  }}\left[ {{\text{AD}} \bot {\text{BC}}} \right]  $ 

 ${\text{AD  =  AD }}\left[ {{\text{Common}}} \right]  $

 $\vartriangle {\text{ABD  }} \cong {\text{ }}\vartriangle {\text{ACD }}\left[ {{\text{RHS rule of congruency}}} \right]  $

${\text{BD  =  DC }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  $

 ${\text{AD bisects BC}}  $ 

(ii) AD bisects A.

Ans: ${\text{Since, }}\angle {\text{BAD  = }}\angle {\text{CAD }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]$

${\text{AD bisects }}\angle {\text{A}}{\text{.}}$

14. Show that in a right angles triangle, the hypotenuse is the longest side.

Ans: Given: Let ABC be a right angled triangle, right angled at B. 

${\text{To prove: Hypotenuse AC is the longest side}}{\text{.}}  $

$\angle {\text{A  +  }}\angle {\text{B  +  }}\angle {\text{C  =   }}\angle {\text{A  +  9}}{{\text{0}}^0}{\text{ + }}\angle {\text{C  =   [}}\angle {\text{ B  =  9}}{{\text{0}}^0}{\text{ ]  }}  $

$\angle {\text{A  +   }}\angle {\text{C  = 18}}{{\text{0}}^0}{\text{  -  9}}{{\text{0}}^0}  $

${\text{ And  }}\angle {\text{B  =  9}}{{\text{0}}^0}  $

${\text{  }}\angle {\text{B  >  }}\angle {\text{C and }}\angle {\text{B  >  }}\angle {\text{A}}  $

${{\text{Since the greater angle has a longer side opposite to it}}{\text{.}}} $ 

$  {{\text{AC  >  AB and AC  >  AB}}} $

Therefore $\angle {\text{B}}$ being the greatest angle has the longest opposite side AC, i.e. hypotenuse.

15. In figure, sides AB and AC of ABC are extended to points P and Q respectively. Also  PBC< QCB. Show that AC > AB.

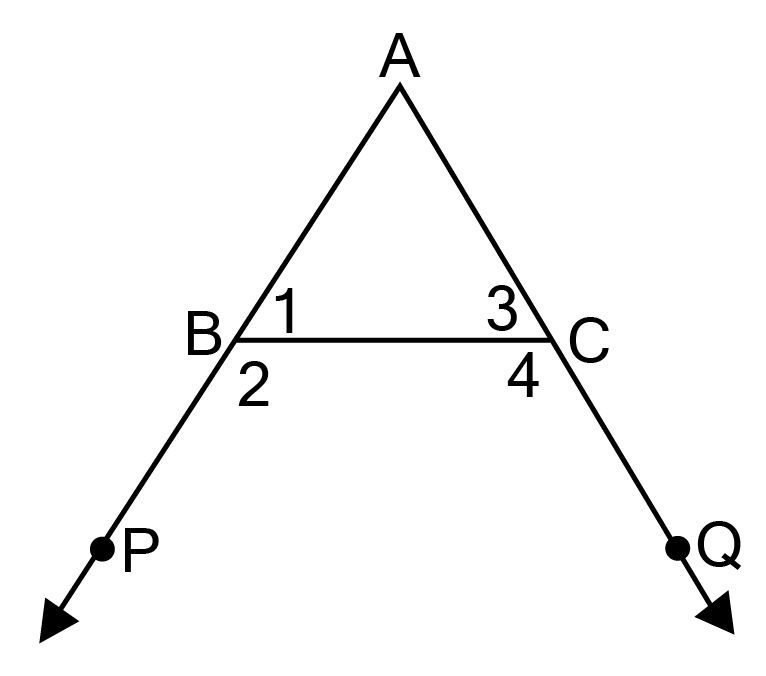
Ans: Given${\text{: In  }}\vartriangle {\text{ABC, }}\angle {\text{PBC <  }}\angle {\text{QCB}}$

${\text{To prove: AC  >  AB}}  $

${\text{Proof: In  }}\vartriangle {\text{ABC,  }}\angle {\text{4  >  }}\angle {\text{2 }}\left[ {{\text{Given}}} \right]  $

${\text{Now }}\angle {\text{1  +  }}\angle {\text{2  =  }}\angle {\text{3  +  }}\angle {\text{4  = 18}}{{\text{0}}^0}{\text{  }}\left[ {{\text{Linear pair}}} \right]{\text{  }}  $

$\angle {\text{1  >  }}\angle {\text{3 [ }}\because \angle {\text{4  > }}\angle {\text{ 2]}}  $

${\text{AC  >  AB }}\left[ {{\text{Side opposite to greater angle is longer}}} \right] $

16. In figure, B < A and C < D. Show that AD < BC.

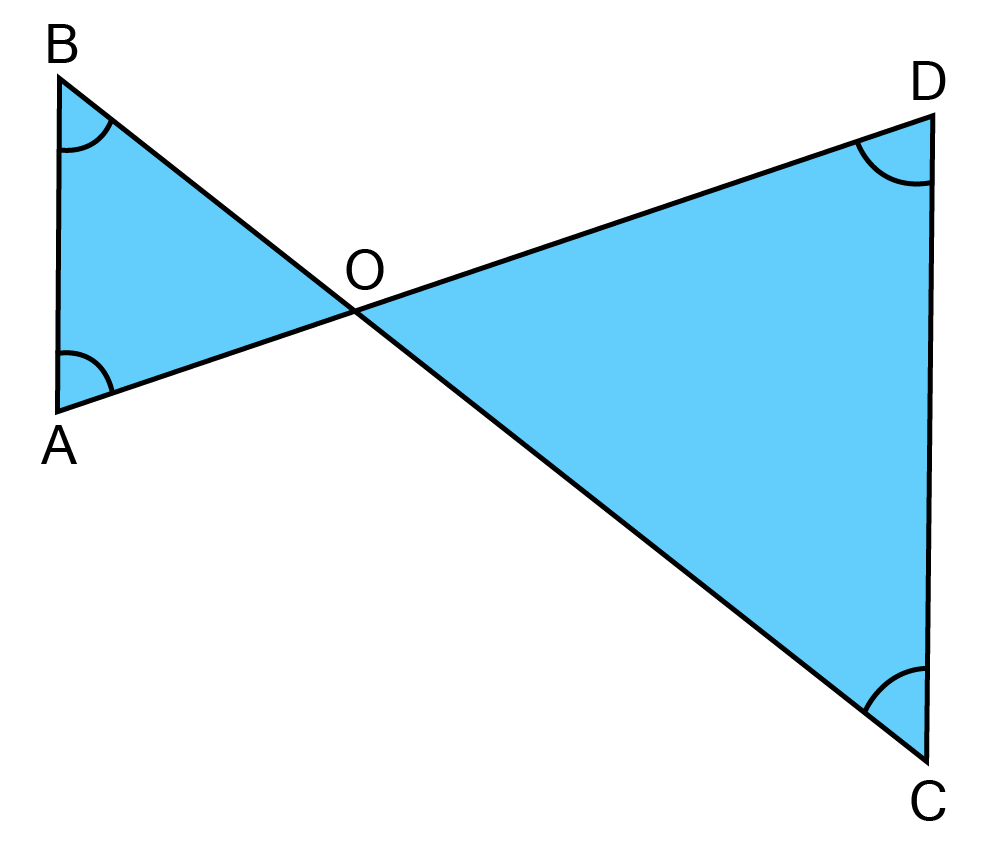
Ans: In $\vartriangle {\text{AOB}}$

$\angle {\text{B  <  }}\angle {\text{A }}\left[ {{\text{Given}}} \right]  $

${\text{OA  <  OB  \ldots  \ldots  \ldots }}{\text{.}}\left( {\text{i}} \right)\left[ {{\text{Side opposite to greater angle is longer}}} \right]  $

${\text{In  }}\vartriangle {\text{COD, }}\angle {\text{C  < }}\angle {\text{ D }}\left[ {{\text{Given}}} \right]  $

${\text{OD  <  OC  }} \ldots  \ldots  \ldots{\text{.}}\left( {{\text{ii}}} \right){\text{ }}\left[ {{\text{Side opposite to greater angle is longer}}} \right]  $

${\text{Adding eq}}{\text{. }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right){\text{, }}  $

${\text{OA  +  OD  <  OB  +  OC}}  $

${\text{AD  <  BC}}  $ 

17. In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.

Ans: Let $\vartriangle {\text{ABC}}$ be a triangle.

${\text{Draw bisectors of  }}\angle {\text{B and   }}\angle {\text{C}}{\text{.}}  $

${\text{Let these angle bisectors intersect each other at point I}}{\text{.}}  $

${\text{ Draw IK}} \bot {\text{BC}}  $

${\text{Also draw IJ}} \bot {\text{AB and IL}} \bot {\text{AC}}{\text{.}}  $

${\text{Join AI}}{\text{. }}  $

${\text{In  }}\vartriangle {\text{BIK and }}\vartriangle {\text{BIJ, }}  $

$\angle {\text{ IKB  =  }}\angle {\text{IJB  = 9}}{{\text{0}}^0}\left[ {{\text{By construction}}} \right]  $

$\angle {\text{ IBK  =  }}\angle {\text{IBJ}}  $

${\text{BI is the bisector of  }}\angle {\text{B }}\left( {{\text{By construction}}} \right){\text{]}}  $ 

 ${\text{ BI  =  BI }}\left[ {{\text{Common}}} \right]  $

  $\vartriangle {\text{BIK  }} \cong {\text{ }}\vartriangle {\text{BIJ }}\left[ {{\text{ASA criteria of congruency}}} \right]  $ 

 ${\text{ IK  =  IJ }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right] \ldots  \ldots  \ldots {\text{.}}\left( {\text{i}} \right)  $

  ${\text{Similarly, }}\vartriangle {\text{CIK  }} \cong {\text{ }}\vartriangle {\text{CIL }}  $

 $\therefore {\text{IK  =  IL }}\left[ {{\text{By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.}}} \right]  \ldots  \ldots  \ldots {\text{.}}\left( {{\text{ii}}} \right)  $

  ${\text{From eq }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right){\text{, }}  $

  ${\text{IK  =  IJ  =  IL}}  $ 

Hence, I is the point of intersection of angle bisectors of any two angles of $\vartriangle {\text{ABC}}$ equidistant from its sides.

18. In quadrilateral ACBD, AB=AD and AC bisects A. show ABC $\cong$ ACD?

Ans: In  $\vartriangle {\text{ABC and }}\vartriangle {\text{ACD,}}$

${\text{AD = AB }}\left( {{\text{Given}}} \right)  $

$\angle {\text{BAC =  }}\angle {\text{CAD \ldots  \ldots }}{\text{. }}\left( {{\text{AC bisects A}}} \right)  $

${\text{And AC =  AC  }}..................{\text{ }}\left( {{\text{Common}}} \right)  $

$\vartriangle {\text{ABC  }} \cong {\text{ }}\vartriangle {\text{ACD}}..............{\text{ }}\left( {{\text{SAS axiom}}} \right)  $ 

19. If DA and CB are equal perpendiculars to a line segment AB. Show that CD bisects AB.

Ans:  In $\vartriangle {\text{AOD and  }}\vartriangle {\text{BOC,}}$

${\text{AD = BC  }}................{\text{ }}\left( {{\text{Given}}} \right)  $

$\angle {\text{A = }}\angle {\text{B and}}  $

$\angle {\text{AOD  =  }}\angle {\text{BOC}}\left( {{\text{vert opp}}{\text{. Angles}}} \right)  $

$\therefore \angle {\text{AOD  =  }}\angle {\text{BOC}}\left( {{\text{AAS rule}}} \right)  $

$\therefore {\text{OA = OB}}\left( {{\text{CPCT}}} \right)  $

${\text{Hence, CD bisects AB}}{\text{.}}  $ 

20. l and m, two parallel lines, are intersected by Another pair of parallel lines p and C. show that $\vartriangle {\mathbf{ABC}}{\text{ }} \cong {\text{ }}\vartriangle {\mathbf{CDA}}.$

Ans: ${\text{L}}\parallel {\text{M and AC cuts them (given)}}$

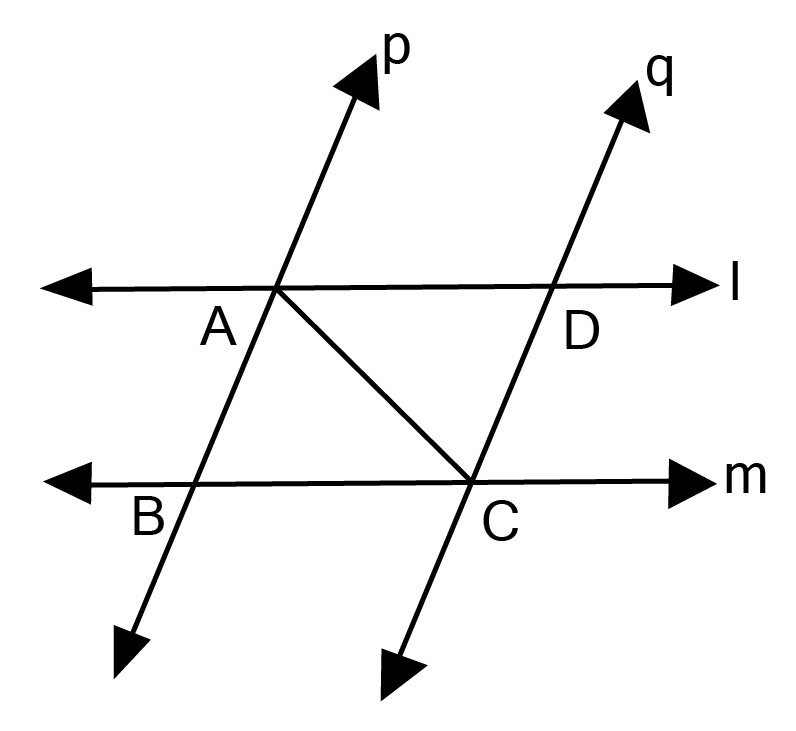
$\therefore \angle {\text{ACB}} = \angle {\text{CAD}}({\text{alternate angles)}}  $

${\text{P }}\parallel {\text{ Q and AC cuts them (Given)}}  $

$\therefore \angle {\text{CAB}} = \angle {\text{ACD}}({\text{Alternate angles)}}  $

${\text{AC = CA(common}})  $

$\therefore \Delta {\text{ABC}} \cong \Delta {\text{CDA}}({\text{ASA rule}})  $ 

21. In fig, the bisector AD of $\Delta {\text{ABC}}$ is $ \bot $ to the opposite side BC at D. show that $\Delta {\text{ABC}}$ is isosceles?

Ans: In $\vartriangle {\text{ABD and }}\vartriangle {\text{ACD}}$

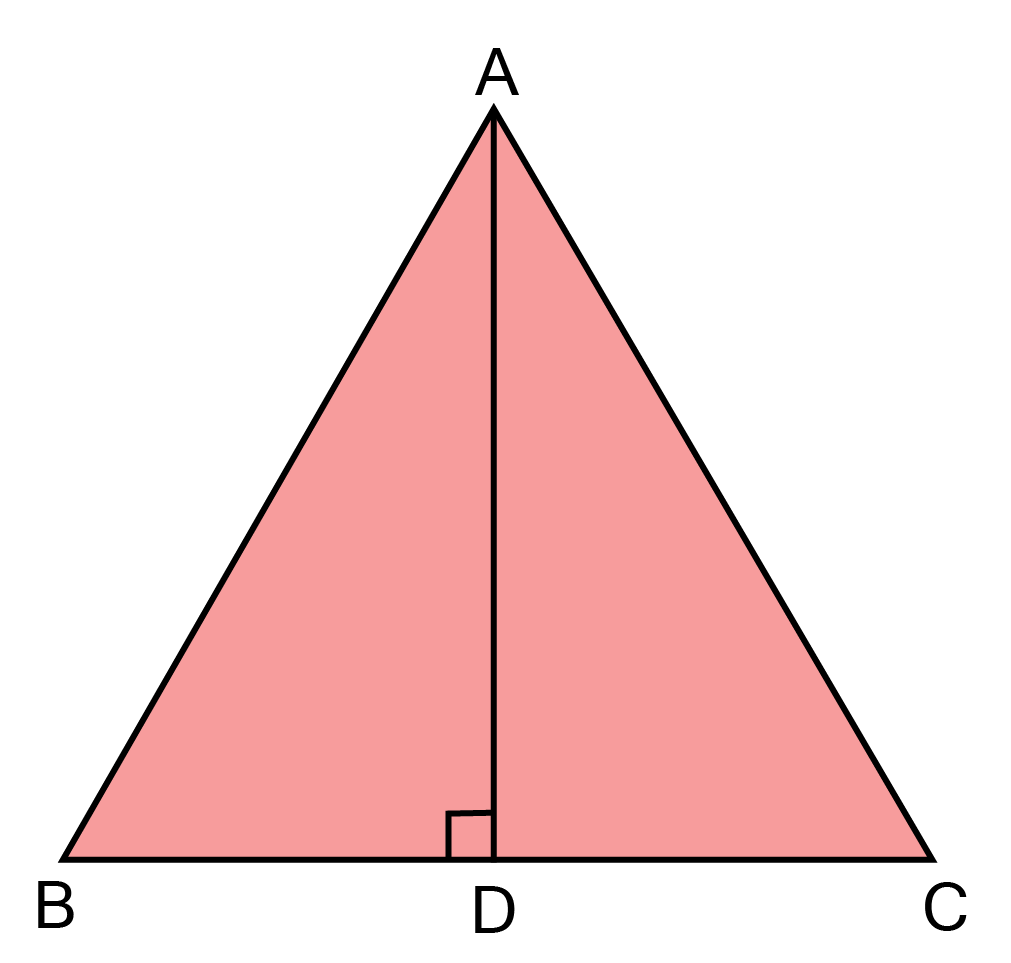
Let  $\angle $BAD = $\angle $1 and $\angle $DAC = $\angle $2

$\angle 1 = \angle 2 \ldots .({\text{AD is the bisector of }}\angle {\text{A}}){\text{ }}  $

${\text{And }}\angle {\text{ADB}} = \angle {\text{ADC}} = {90^\circ } \ldots  \ldots  \ldots ({\text{AD}} \bot {\text{BC}})  $

$\therefore {\text{AD = AD}} \ldots  \ldots .({\text{ common }})  $

$\vartriangle {\text{ABD}} \cong \vartriangle {\text{ACD}} \ldots  \ldots {\text{ (ASA rule)}}  $

${\text{ }}\therefore {\text{AB}} = {\text{AC}}\quad {\text{ (C}}{\text{.P}}{\text{.C}}{\text{.T) }}  $

${\text{ Hence }}\vartriangle {\text{ABC is isosceles}}{\text{. }}  $ 

22. If AE=AD and BD=CE. Prove that $\vartriangle $AEB$ \cong $$\vartriangle $ADC

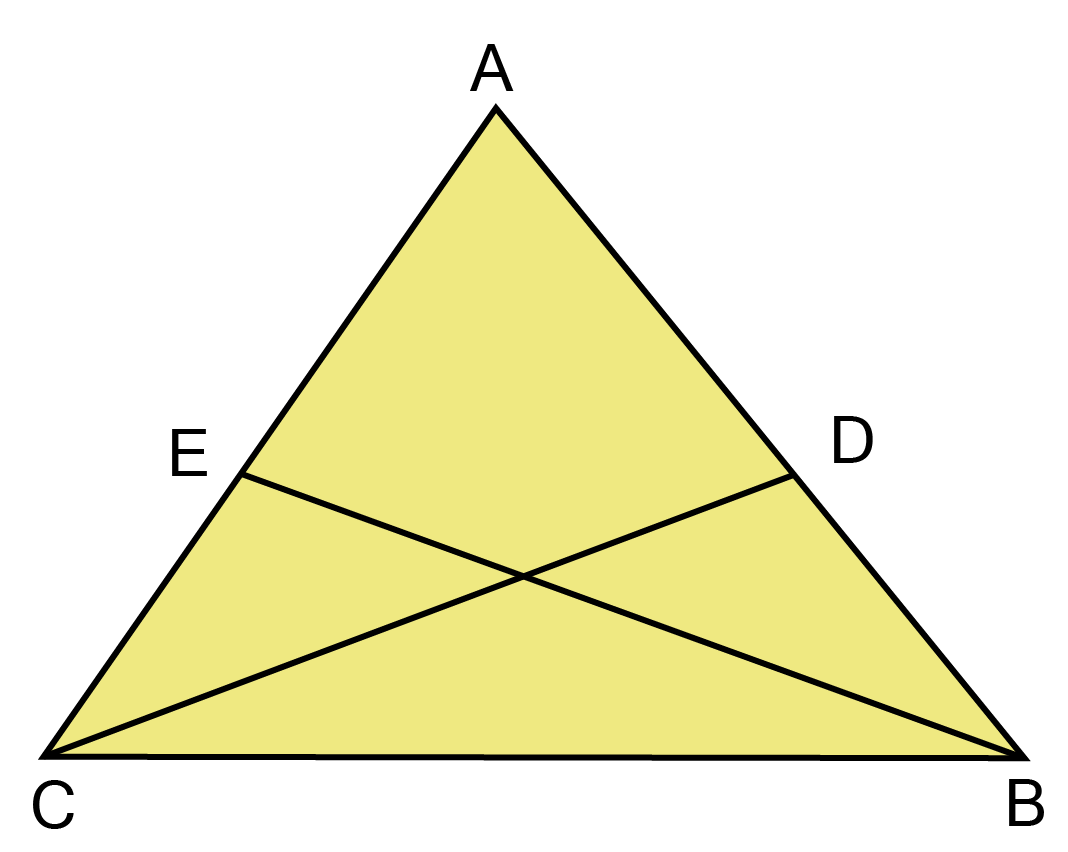
 Ans: We have,

 ${\text{AE}} = {\text{ADandCE}} = {\text{BD}}  $

 $\Rightarrow {\text{AE}} + {\text{CE}} = {\text{AD}} + {\text{BD}}  $

 $\Rightarrow {\text{AC}} = {\text{AB}}({\text{i}})  $

  ${\text{Now,in}}\Delta {\text{AEBand}}\vartriangle {\text{ADC}},  $

  ${\text{AE}} = {\text{AD}}[{\text{given}}]  $

  $\angle {\text{EAB}} = \angle {\text{DAC}}[{\text{common}}]  $

  ${\text{AB}} = {\text{AC}}[{\text{from}}({\text{i}})]  $

  ${\text{AE}} = {\text{AD}}[{\text{given}}]  $

  $\angle {\text{EAB}} = \angle {\text{DAC}}[{\text{common}}]  $

  ${\text{AB}} = {\text{AC}}[{\text{from}}(i)]  $ 

$\vartriangle {\text{AEB}} \cong \vartriangle {\text{ADC[by SAS]}}$

23. In quadrilateral ACBD, AC=AD and AB bisects $\angle $A. show that $\vartriangle {\text{ABC}} \cong {\text{ }}\vartriangle {\text{ABD}}$. What can you say about BC and BD?

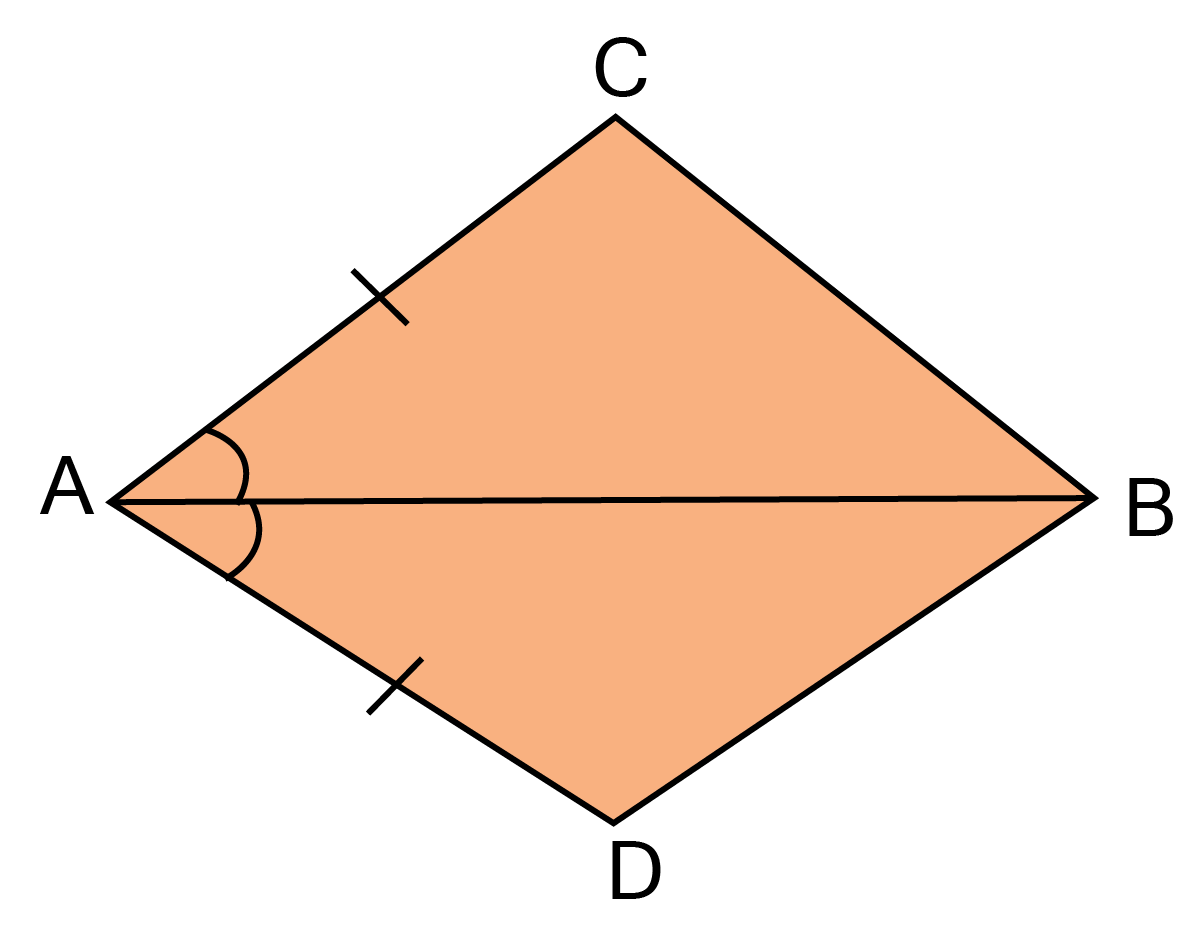
Ans: In $\vartriangle {\text{ABC}} \cong {\text{ }}\vartriangle {\text{ABD}}$,

${\text{AC = AD }}\left[ {{\text{given}}} \right]  $

$\angle {\text{CAB  = }}\angle {\text{DAB}}\left[ {{\text{AB bisects }}\angle {\text{A}}} \right]  $

${\text{AB = AB }} [ {{\text{common}}}]  $

$\vartriangle {\text{ABC }} \cong {\text{ }}\vartriangle {\text{ABD }}\left[ {{\text{SAS criterion}}} \right]  $

$\therefore {\text{BC = BD }}\left[ {{\text{CPCT}}} \right]  $ 

24. In $\vartriangle {\text{ABC}}$, the median AD is $ \bot $ to BC. Prove that $\vartriangle {\text{ABC}}$ is an isosceles triangle

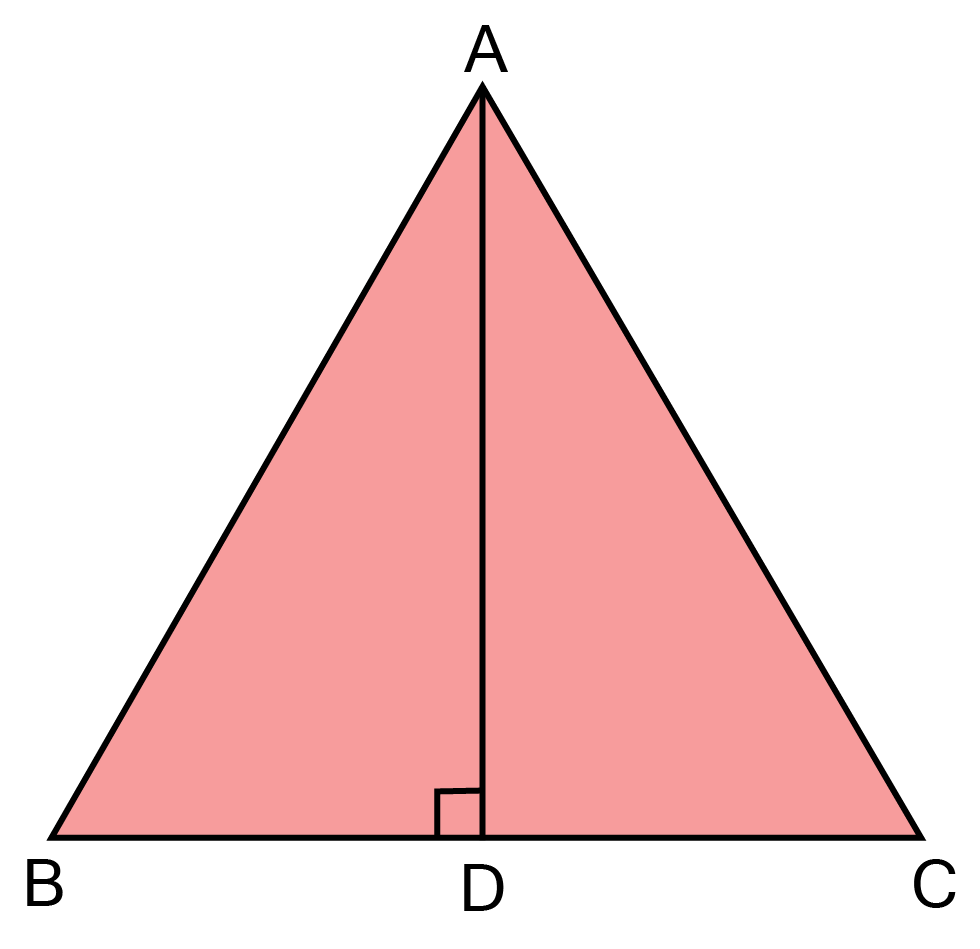
Ans: In $\vartriangle {\text{ABD and }}\vartriangle {\text{ACD}}$

${\text{ BD  = CD }}\left[ {{\text{D is mid - point of BC}}} \right]  $

${\text{AD = AD }}\left[ {{\text{Common}}} \right]  $ 

$\left. {\angle {\text{ADB}} = \angle {\text{ADC}}[{\text{each9}}{{\text{0}}^\circ }\because {\text{AD}} \bot {\text{BC}}} \right]  $

$\vartriangle {\text{ABD}} \cong \vartriangle {\text{ACD}}[{\text{BySAS}}]  $

$\therefore {\text{AB = AC}}[{\text{CPCT}}]  $

${\text{Hence}},{\text{triangle ABC is an isosceles triangle}}.  $ 

25. Prove that ABC is isosceles if altitude AD bisects BAC

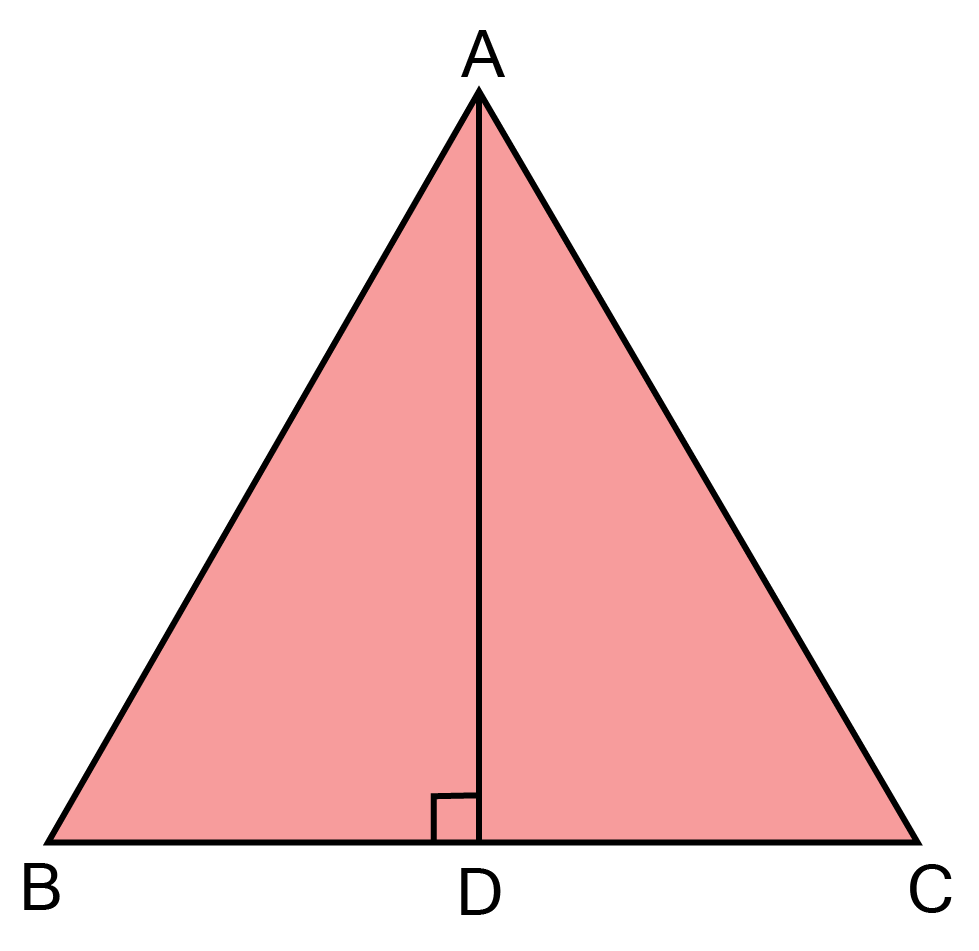
Ans: In $\vartriangle {\text{ABD and }}\vartriangle {\text{ACD}}$

$\angle {\text{ADB = }}\angle {\text{ADC}}\left[ {{\text{ Each 9}}{{\text{0}}^\circ }{\text{,AD}} \bot {\text{BC}}} \right]  $

$\angle {\text{BAD = }}\angle {\text{CAD}}[{\text{AD bisects }}\angle {\text{BAC}}]  $

${\text{AD = AD}}[{\text{common}}]  $

$\vartriangle {\text{ABD}} \cong \vartriangle {\text{ACD}}[{\text{ByAAS}}]  $

$ \Rightarrow {\text{AB = AC}}[{\text{CPCT}}]  $

${\text{ Thus, }}\vartriangle {\text{ABC is an isosceles triangle}}{\text{. }}  $ 

26. ABC is An isosceles triangle in which altitudes BE and CF are drawn to side AC and AB respectively. Show that these altitudes are equals.

Ans: In $\vartriangle {\text{ABE and }}\vartriangle {\text{ACF}}$, 

$\angle {\text{A = }}\angle {\text{A}}\left[ {{\text{Common}}} \right]  $

$\angle {\text{AEB = }}\angle {\text{AFC = 9}}{{\text{0}}^0}  $

${\text{AB = AC}}[{\text{given}}]  $

$\vartriangle {\text{ABE}} \cong \vartriangle {\text{ACF}}[{\text{ByAAS}}]  $

$ \Rightarrow {\text{BE = CF}}[{\text{CPCT}}]  $ 

27. If AC= AE, AB=AD and $\angle {\text{BAD}} = \angle {\text{EAC}}$show that BC =DE.

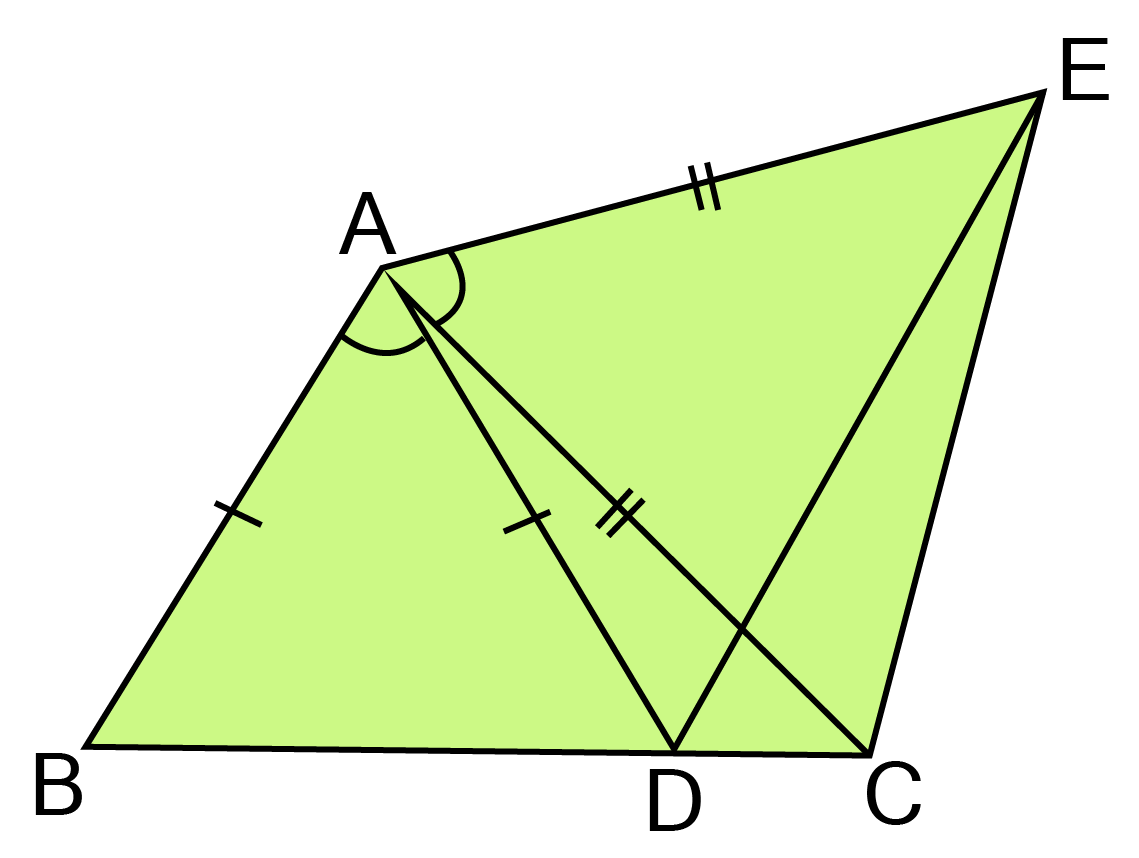
Ans: In $\vartriangle {\text{BAC and}}\vartriangle {\text{DAE,}}$

${\text{AB = AD}}[{\text{given}}]{\text{ }}  $

${\text{AC }} = {\text{AE}}[{\text{given}}]{\text{ }}  $

${\text{Also, }}\angle {\text{BAD}} = \angle {\text{EAC}}[{\text{given}}]  $

$\therefore \angle {\text{BAC}} + \angle {\text{DAC}} = \angle {\text{EAC}} + \angle {\text{CAD}}  $

$\Rightarrow \angle {\text{BAC}} = \angle {\text{EAD}}  $

$\therefore \vartriangle {\text{BAC}} \cong \vartriangle {\text{DAE}}{\text{          [SAS  criterion}}]  $

 $\Rightarrow {\text{BC = DE     [CPCT}}]  $ 

28. Line $\angle $ is the bisector of an angle $\angle $A and $\angle $B is any point on line l. BP and BQ are from $\angle $B to the arms of $\angle $A show that : 

(i). $\vartriangle {\text{APB}} \cong {\text{ }}\vartriangle {\text{AQB}}$

Ans: In $\vartriangle {\text{APB}} \cong {\text{ }}\vartriangle {\text{AQB}}$,

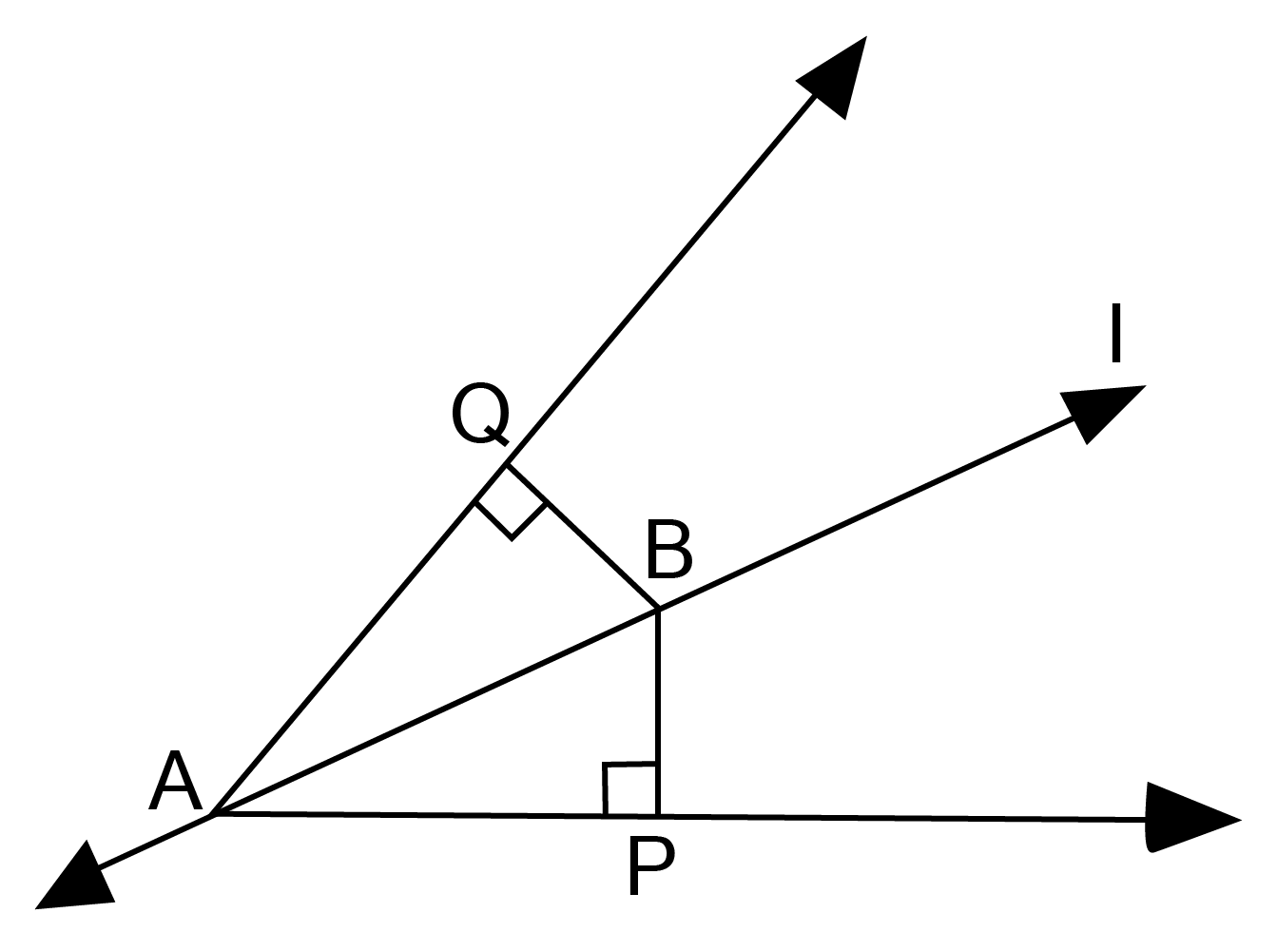
$ \angle {\text{BAP  =  }}\angle {\text{BAQ [given]}}  $

$ \angle {\text{APB  =  }}\angle {\text{AQB = 9}}{{\text{0}}^0}[{\text{common}}]  $

${\text{AB = AB[common]}} $ 

$\therefore \vartriangle {\text{APB}} \cong {\text{ }}\vartriangle {\text{AQB}}[{\text{AAS rule}}]$

(ii). BP = BQ or B is A equidistant from the arms of $\angle $A

Ans: ${\text{BP = BQ[CPCT]}}$

29. In the given figure, $\vartriangle {\text{ABC}}$ is an isosceles triangle and $\angle B = {75^0}$, find x.

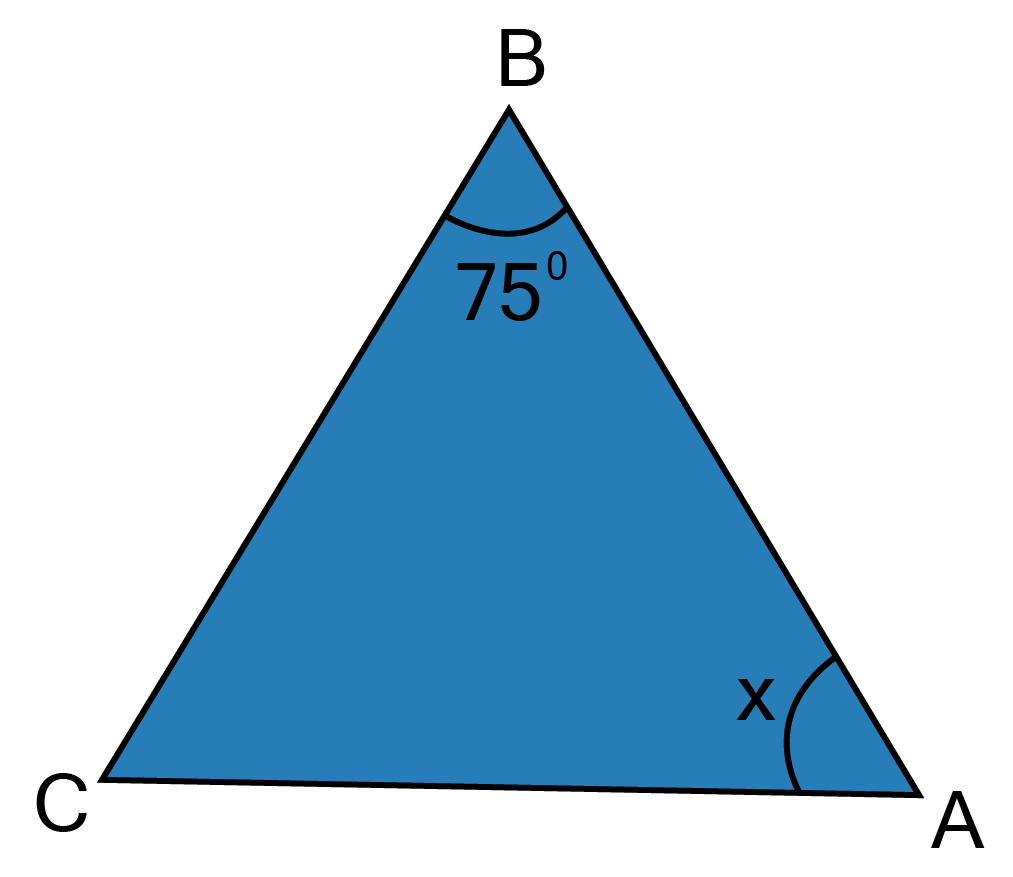
Ans: In $\vartriangle {\text{ABC}}$, 

${\text{AB}} = {\text{AC}}  $

$ \Rightarrow \angle B = \angle C[{\text{Angles opposite to equal sides are equal}}]  $

$\therefore \angle B = {75^\circ }  $

$\therefore \quad \angle B = \angle C = {75^\circ }  $

$\angle A + \angle B + \angle C = {180^\circ }  $

$x + 150 = {180^\circ }  $

$x = {30^\circ }  $ 

30. If E> A and C> D. prove that AD>EC.

Ans: In $\vartriangle {\text{ABE}}$,

$\angle {\text{E}} > \angle {\text{A }}[{\text{given}}]$

$\Rightarrow AB > EB[{\text{Side opposite to greater angle is larger}}].....(i)  $

${\text{Similarly,in }}\Delta {\text{BCD,}}  $

$\angle C > \angle D [{\text{ Given ]}} $ 

$ \Rightarrow BD > BC ………………………………...(ii) $

${\text{Adding (i) and (ii}})  $

${\text{AB + BD}} > {\text{EB + BC}}  $

${\text{or AD}} > {\text{EC}}  $ 

31. If PQ= PR and S is any point on side PR. Prove that RS<QS.

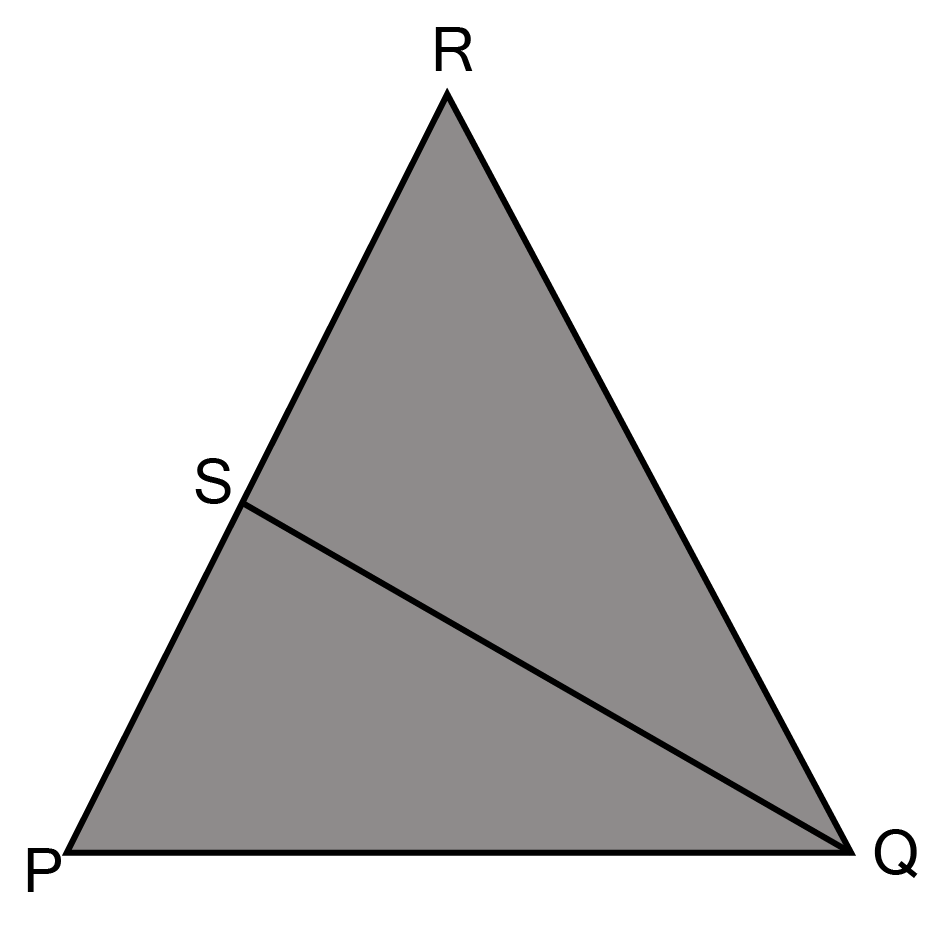
Ans: In $\vartriangle {\text{PQR}}$

${\text{PQ - PR[given]}}  $

$\angle {\text{PRQ = }}\angle {\text{PQR[angle opposite to equal side are equal]}}  $

${\text{Now,}}\angle {\text{SQR < }}\angle {\text{PQR[}}\angle {\text{SQR is a part of }}\angle {\text{PQR]}}  $

$\angle {\text{SQR < }}\angle {\text{PRQ or }}\angle {\text{SRQ}}  $

 $\Rightarrow {\text{RS < QS[side opposite to smaller angle in}} \Delta SRQ] $ 

32. Prove that MN+NO +OP+PM>2MO.

Ans: In $\vartriangle {\text{MON}}$

${\text{MN + NO > MO[Sum of any two side of}} \Delta {\text{ is greater than third sides]}}......{\text{(i)}}  $

${\text{Similarly in}} \Delta MPQ  $

${\text{OP + PM > MO}}  $

${\text{Hence from (i) and (ii) }}  $

${\text{or MN + NO + OP + PM > 2MO}}  $ 

33. Prove that MN+NO+OP>PM.

Ans: In $\vartriangle {\text{MON}}$

${\text{MN + NO > MO [Sum of any two side of}} \Delta {\text{  is greater than third sides]}}........{\text{(i)}}  $

${\text{Similarly in}} \Delta MOQ,  $

${\text{MO + OP > PM}}......{\text{(ii)}}  $

${\text{Hence from (i) and (ii) }}  $

${\text{or MN + NO + OP + MO > MO + PM}}  $

${\text{or MN + NO + OP > PM}}  $ 

34. $\vartriangle {\text{ABC}}$ is an equilateral triangle and $\angle B = {60^0}$, find $\angle C$ .

Ans: In $\vartriangle {\text{ABC}}$,

${\text{AB = AC}}  $

$\angle {\text{B = }}\angle {\text{C[angle opposite to equal sides are equal]}}  $

${\text{but }}\angle B = {60^0}  $

$so,\angle C = {60^0}  $ 

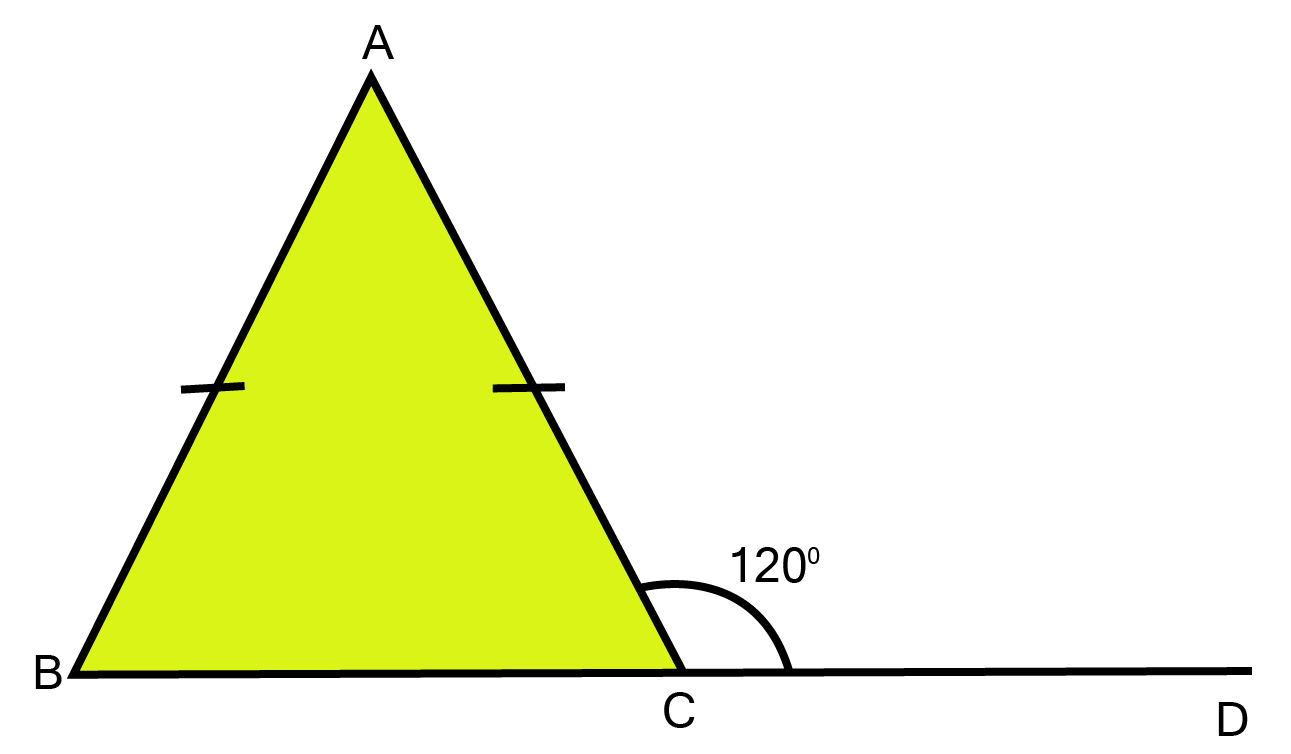
35. In the figure, AB = AC and $\angle ACD = {120^0}$, find $\angle B$ .

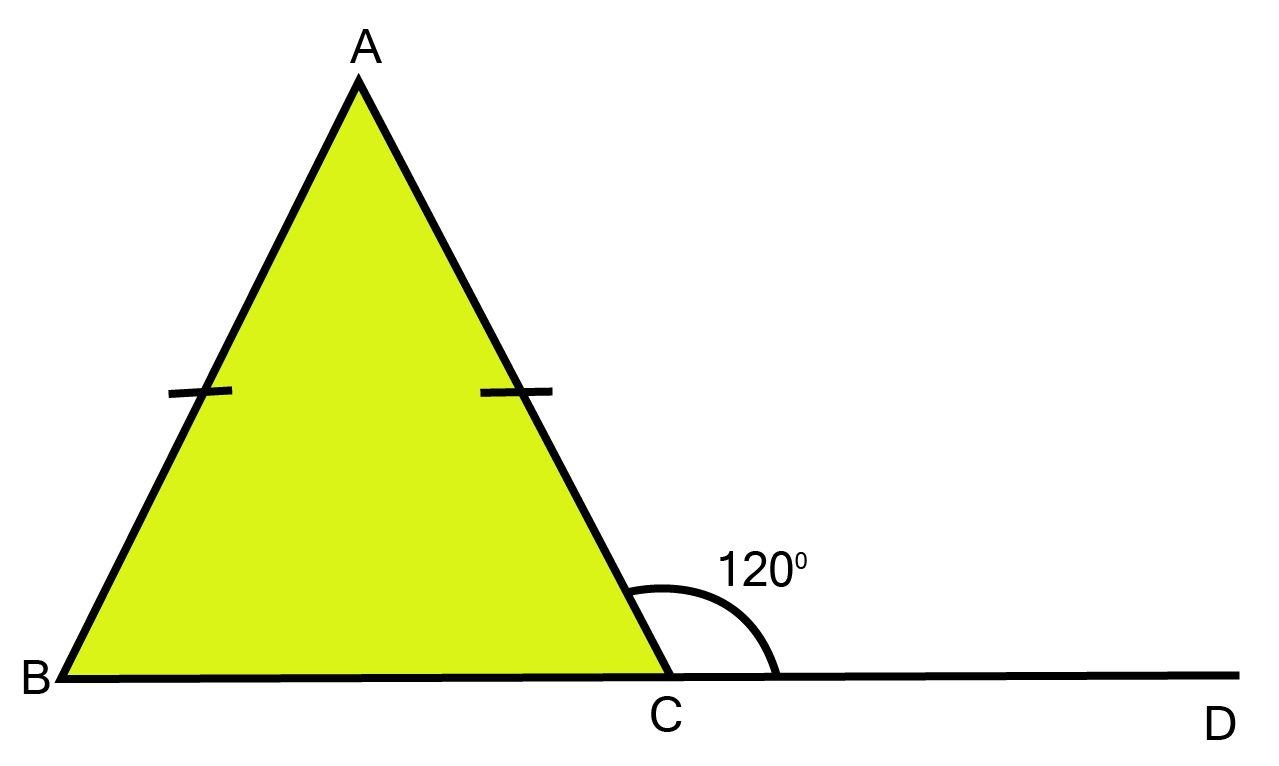
Ans: Since, in $\vartriangle ABC$, AB=AC

$\angle {\text{B = }}\angle {\text{C          [angle opposite to equal sides are equal]}}  $

$ {\text{but }}\angle ACB + \angle ACD = {180^0}           [{\text{Linear pair}}]  $

$  so,\vartriangle ACB = {180^0} - {120^0}  $

 $ and,\angle C = \angle B = {60^0}  $ 

36. In the given figure, find $\angle A$

Ans: In $\vartriangle ABC$

$\angle A + \angle B + \angle C = {180^0}[{\text{sum of angles of a triangle}}]  $

$\angle A + {60^0} + {60^0} = {180^0}  $

$\Rightarrow \angle A = {180^0} - {120^0}  $

$\angle A = {60^0}  $ 

3 Marks Questions

1. Prove that in a right triangle, hypotenuse is the longest (or largest) side.

Given a right angled triangle ABC in which $\angle B = {90^0}$ 

Therefore, AC is hypotenuse.

Now,since  

${\angle B = {{90}^\circ }} $ 

${\therefore A + \angle B + \angle C = {{180}^\circ }} $ 

${\angle A + \angle C = {{180}^\circ } - {{90}^\circ } = {{90}^\circ }} $ 

${{\text{ ie}}{\text{. }}\angle B = \angle A + \angle C} $ 

${ \Rightarrow \angle B > \angle A{\text{ and }}\angle B > \angle C} $

${\therefore AB = BC = AC \Rightarrow AB = BC} $ 

${ \Rightarrow \angle C = \angle A \ldots  \ldots  \ldots (i)} $ 

${{\text{ Similarly, }}AB = AC} $ 

${ \Rightarrow \angle C = \angle B \ldots  \ldots  \ldots .{\text{ (ii) }}} $

From eq.(i)and(ii),  

$\angle {\text{A}} = \angle {\text{B}} = \angle {\text{C}}$

$Now in \vartriangle ABC  $

${\angle {\text{A}} + \angle {\text{B}} + \angle {\text{C}} = {{180}^\circ } \ldots  \ldots  \ldots ({\text{iv}})} $ 

${ \Rightarrow \angle {\text{A}} + \angle {\text{A}} + \angle {\text{A}} = {{180}^\circ } \Rightarrow 3\angle {\text{A}} = {{180}^\circ }} $ 

${ \Rightarrow \angle {\text{A}} = {{60}^\circ }} $ 

${{\text{ Since }}\angle {\text{A}} = \angle {\text{B}} = \angle {\text{c[From eq}}.({\text{iii}})]} $ 

${\therefore \angle {\text{A}} = \angle {\text{B}} = \angle c = {{60}^\circ }} $ 

2. Show that the angles of an equilateral triangle are 60 degree each.

Ans: Let ABC be an equilateral triangle.

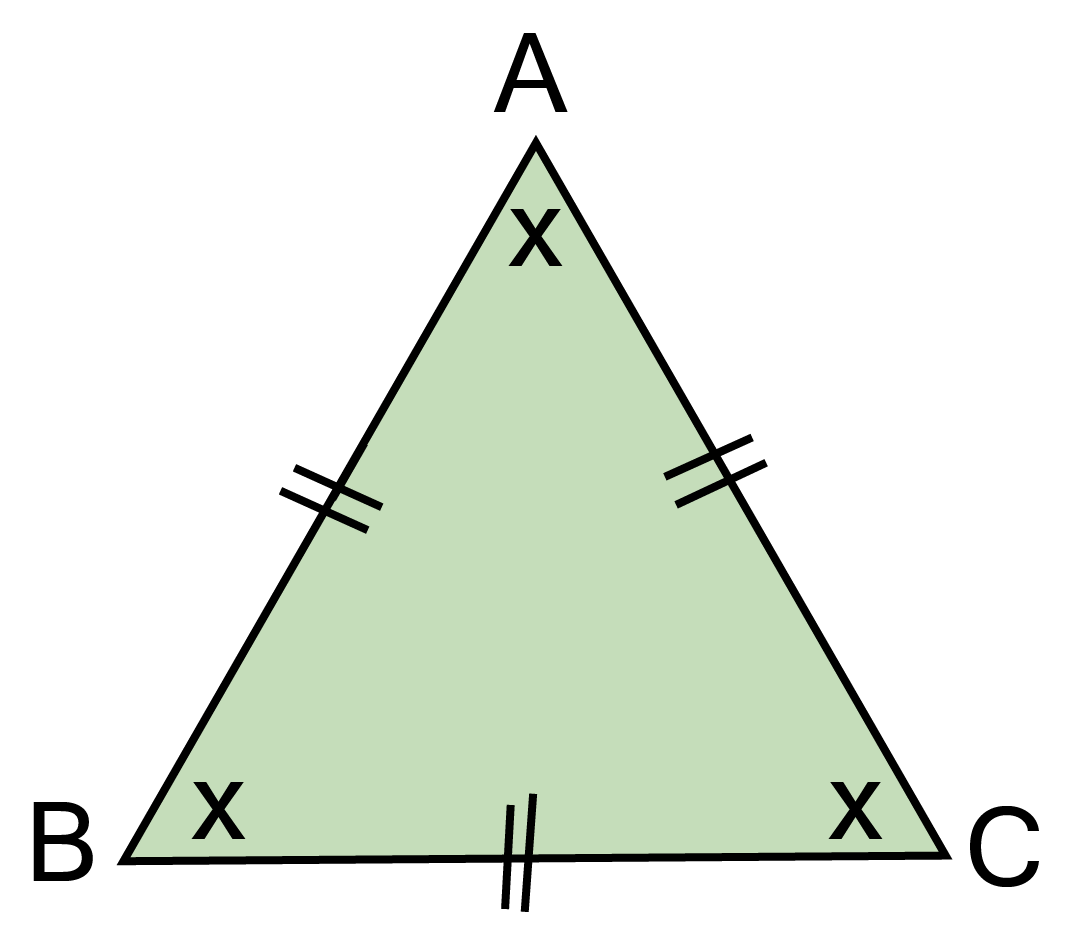
${\therefore AB = BC = AC \Rightarrow AB = BC} $ 

${ \Rightarrow \angle C = \angle A \ldots  \ldots ...(i)} $ 

${{\text{ Similarly, }}AB = AC} $ 

${ \Rightarrow \angle C = \angle B. \ldots  \ldots .6ii)} $

  ${\text{From eq}}{\text{.(i) and (ii)}}{\text{.}}  $

  $\angle {\text{A}} = \angle {\text{B}} = \angle C  $

  ${\text{Now\_in\_}}\vartriangle {\text{ABC}}  $

  ${\angle {\text{A}} + \angle {\text{B}} + \angle {\text{C}} = {{180}^\circ } \ldots  \ldots ..{\text{ (iv) }}} $ 

 $\Rightarrow \angle {\text{A}} + \angle {\text{A}} + \angle {\text{A}} = {180^\circ }  $

 $\Rightarrow 3\angle {\text{A}} = 180  $ 

  ${ \Rightarrow \angle {\text{A}} = {{60}^\circ }} $ 

${{\text{ Since }}\angle {\text{A}} = \angle {\text{B}} = \angle {\text{C}}[F{\text{rom eq}}{\text{. }}({\text{iii}})]} $ 

${\therefore \angle {\text{A}} = \angle {\text{B}} = \angle {\text{C}} = {{60}^\circ }} $ 

Hence, each angle of equilateral triangle is ${60^0}$

3. $\vartriangle {\text{ABC and }}\vartriangle {\text{DBC}}$ are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See figure). If AD is extended to intersect BC at P, show

that:

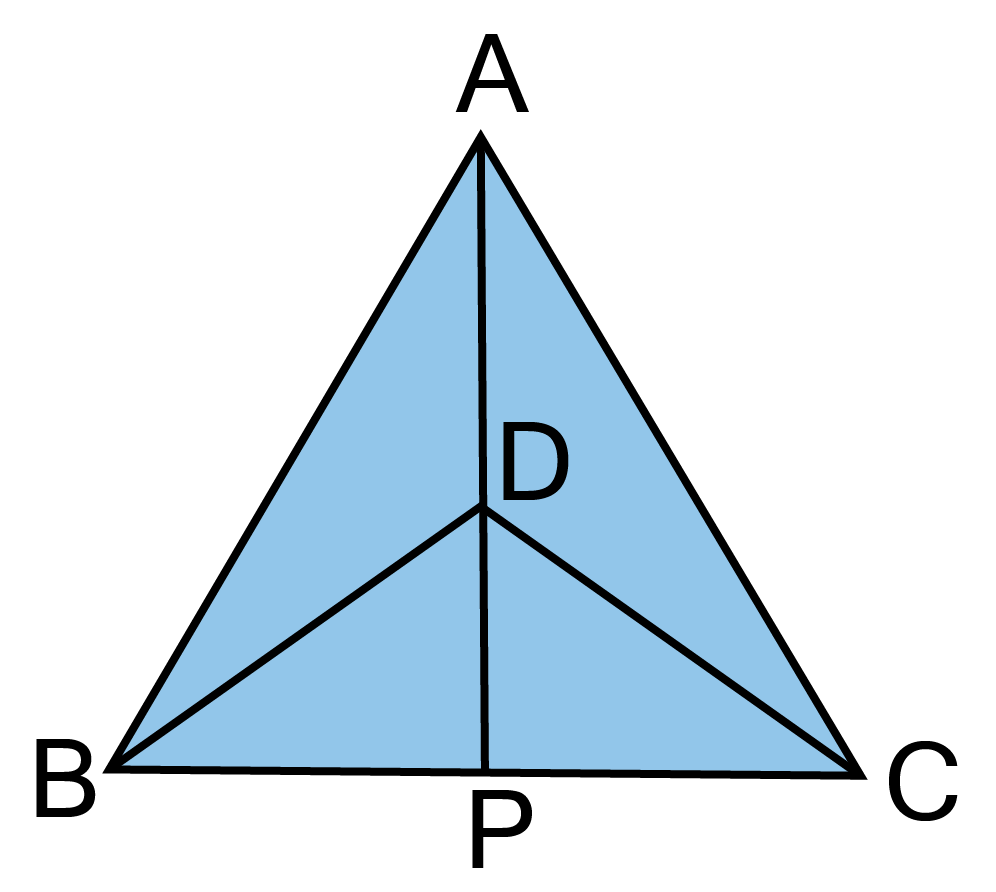
(i). $\vartriangle {\text{ABD }} \cong {\text{ }}\vartriangle {\text{ACD}}$

$\vartriangle {\text{DBC is}} {\text{an}} {\text{isosceles}} {\text{triangle}}{\text{.}}  $

${\text{BD}} = {\text{CD}}  $

${\text{Now}} {\text{in}}\vartriangle A{\text{BD}} {\text{and}} \vartriangle {\text{ACD}},  $

AB = AC               [Given]  

$  {\text{BD}} = {\text{CD}}               [Given]  $

${\text{AD}} = {\text{AD}}                [{\text{Common}}]  $

$\therefore  \vartriangle {\text{ABD}} \cong \Delta ACD          [By SSS {\text{congruency}}]  $

$\Rightarrow \angle {\text{BAD}} = \angle {\text{CAD}}[{\text{By}} C.P.C.T.] \ldots  \ldots ..({\text{i}})  $ 

(ii). $\vartriangle {\text{ABP}}  \cong  \vartriangle {\text{ACP}}$

${\text{Now}} {\text{in}} \vartriangle {\text{ABP}} {\text{and}} \vartriangle {\text{ACP,}}  $

$AB = AC[{\text{Given]}}  $

$\angle BAD = \angle CAD[{\text{From eq}}.(i)]  $ 

${\text{AP}} = {\text{AP}}  $

$\therefore \vartriangle {\text{ABP}} = \vartriangle {\text{ACP}}[{\text{By SAS congruency}}]  $ 

(iii). AP bisects $\angle A$as well as $\angle D$

Ans: since $\vartriangle {\text{ABP }} \cong {\text{ }}\vartriangle {\text{ACP}}$

$\Rightarrow \angle {\text{ BAP }} = \angle {\text{CAP}}[{\text{ByC}}.{\text{P}}.{\text{C}}.{\text{T}}.]  $

$\Rightarrow {\text{ AP bisects }}\angle {\text{A}}{\text{.  }}  $

${\text{Since }}\Delta {\text{ABD}} \cong \Delta {\text{ACD}}[{\text{Frompart}}({\text{i}})]  $

$\Rightarrow \angle {\text{ADB}} = \angle {\text{ADC}}[{\text{ByC}}.{\text{P}}.{\text{C}}.{\text{T}}.] \ldots  \ldots  \ldots {\text{ (ii) }}  $

${\text{ Now }}\angle {\text{ADB}} + \angle {\text{BDP}} = {180^\circ }[{\text{Linearpair}}]..........({\text{iii}})  $

${\text{ And }}\angle {\text{ADC}} + \angle {\text{CDP}} = {180^\circ }[{\text{Linearpair}}]..........({\text{iv}})  $

${\text{Fromeq}}.({\text{iii}}){\text{and}}({\text{iv}}),  $

$\angle {\text{ADB}} + \angle {\text{BDP}} = \angle {\text{ADC}} + \angle {\text{CDP}}  $

$\Rightarrow \angle {\text{ADB}} + \angle {\text{BDP}} = \angle {\text{ADB}} + \angle {\text{CDP}}[{\text{Using}}({\text{ii}})]  $

$\Rightarrow \angle {\text{BDP}} = \angle {\text{CDP}}  $

$\Rightarrow {\text{DP bisects }}\angle {\text{D or AP bisects }}\angle {\text{D}}.  $ 

(iv). AP is the perpendicular bisector of BC.

Ans: 

$\therefore {\text{BP}} = {\text{PC}}[{\text{ByC}}.{\text{P}}.{\text{C}}.{\text{T}}.]  $

 $ {\text{ And }}\angle {\text{APB}} = \angle {\text{APC}}[{\text{ByC}}.{\text{P}}.{\text{C}}.{\text{T}}.].........({\text{vi}})  $

 $ {\text{ Now }}\angle {\text{APB}} + \angle {\text{APC}} = {180^\circ }[{\text{Linear Pair}}]  $

  $\left. { \Rightarrow \angle {\text{APB}} + \angle {\text{APC}} = {{180}^\circ }[{\text{Usingeq}}.({\text{vi}})} \right]  $

  $ \Rightarrow 2\angle {\text{APB}} = {180^\circ }  $

  $ \Rightarrow \angle {\text{APB}} = {90^\circ }  $ 

$ \Rightarrow {\text{AP}} \bot {\text{BC}}............{\text{(vii)}}$

From eq. (v), we have BP $ \bot $ PC and from (vii), we have proved ${\text{AP}} \bot {\text{BC}}$. So, collectively AP is perpendicular bisector of BC.

4. Two sides AB and BC and median AM of the triangle ABC are respectively equal to side PQ and QR and median PN of PQR (See figure). Show that:  ABM $\cong$ PQN 

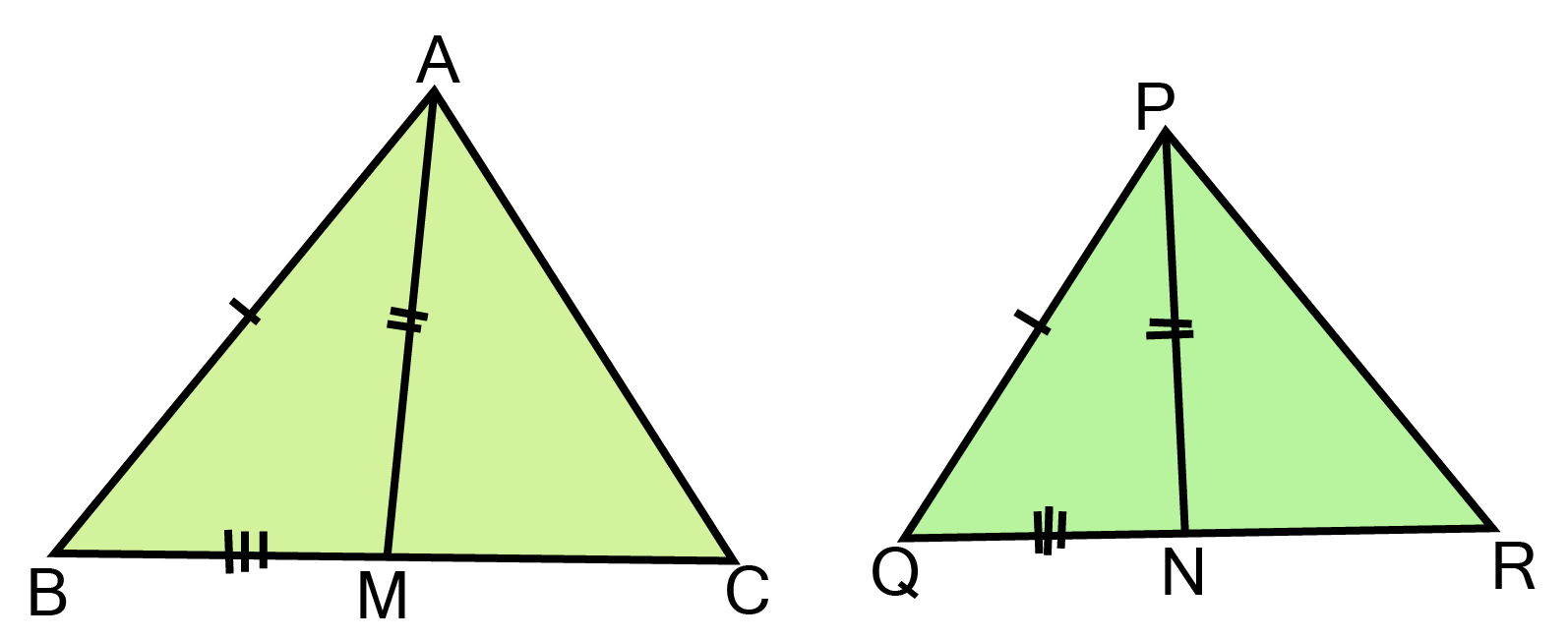
Ans: $A{\text{M}} {\text{is}} {\text{the}} {\text{median}} {\text{of triangle ABC}}  $

 $ \therefore {\text{BM}} = {\text{MC}} = \dfrac{1}{2}{\text{BC}} \ldots  \ldots  \ldots ({\text{i}})  $

${\text{PN }} {\text{is }} {\text{the}} {\text{ median }} {\text{ of }}\delta {\text{PQR}}  $

$\therefore QN = NR = \dfrac{1}{2}QR \ldots  \ldots  \ldots (ii)  $

  Now ${\text{BC}} = {\text{QR}}[{\text{ Given}}]  $

   $\Rightarrow \dfrac{1}{2}{\text{BC}} = \dfrac{1}{2}{\text{QR}}  $

  $\therefore {\text{BM}} = {\text{QN}}  $ 

(i). $\vartriangle ABM \cong \vartriangle PQN$

Now in $\vartriangle ABM \cong \vartriangle PQN$,

${\text{AB = PQ[given]}}  $

${\text{AM = PN[given]}}  $

${\text{BM = QN[from  eq}}{\text{.(iii)]}}  $

$\therefore \vartriangle ABM \cong \vartriangle PQN[{\text{by SSS congruency}}]  $

$\Rightarrow \angle B = \angle Q[by{\text{ CPCT}}]........(iv)  $ 

(ii). $\vartriangle ABC \cong \vartriangle PQR$

In  $ABC{\text{ }}and{\text{ }}\vartriangle PQR$

${\text{AB = PQ[given]}}  $

$\angle B{\text{ = }}\angle {\text{Q[proven above]}}  $

${\text{BC = QR[given]}}  $

$\therefore \vartriangle ABC \cong \vartriangle PQR[{\text{by SAS congruency}}]  $ 

5. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Ans: In $\vartriangle BEC{\text{ and }}\vartriangle CFB,$

$\angle BEC{\text{  = }}\angle CFB[each\,{\text{ }}{90^0}]$

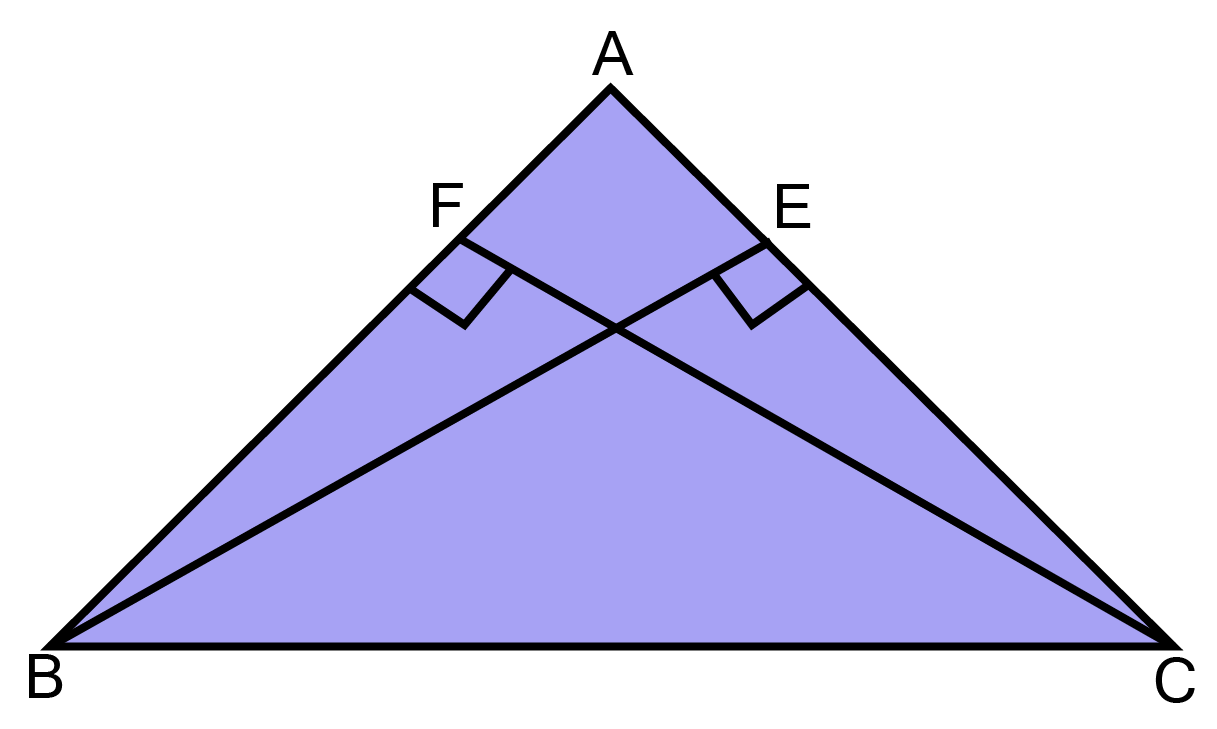
${\text{BC = BC          [Common]}}  $

${\text{BE = CF       [Given]}}  $

${\Delta\text{ BEC}} \cong \Delta{\text{ CFB[RHScongruency]}}  $

$\Rightarrow {\text{EC = FB[By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.]}}.....{\text{(i)}}  $ 

6. ABC is an isosceles triangles with AB = AC. Draw AP$ \bot $ BC and show that $\angle $B = $\angle $C.

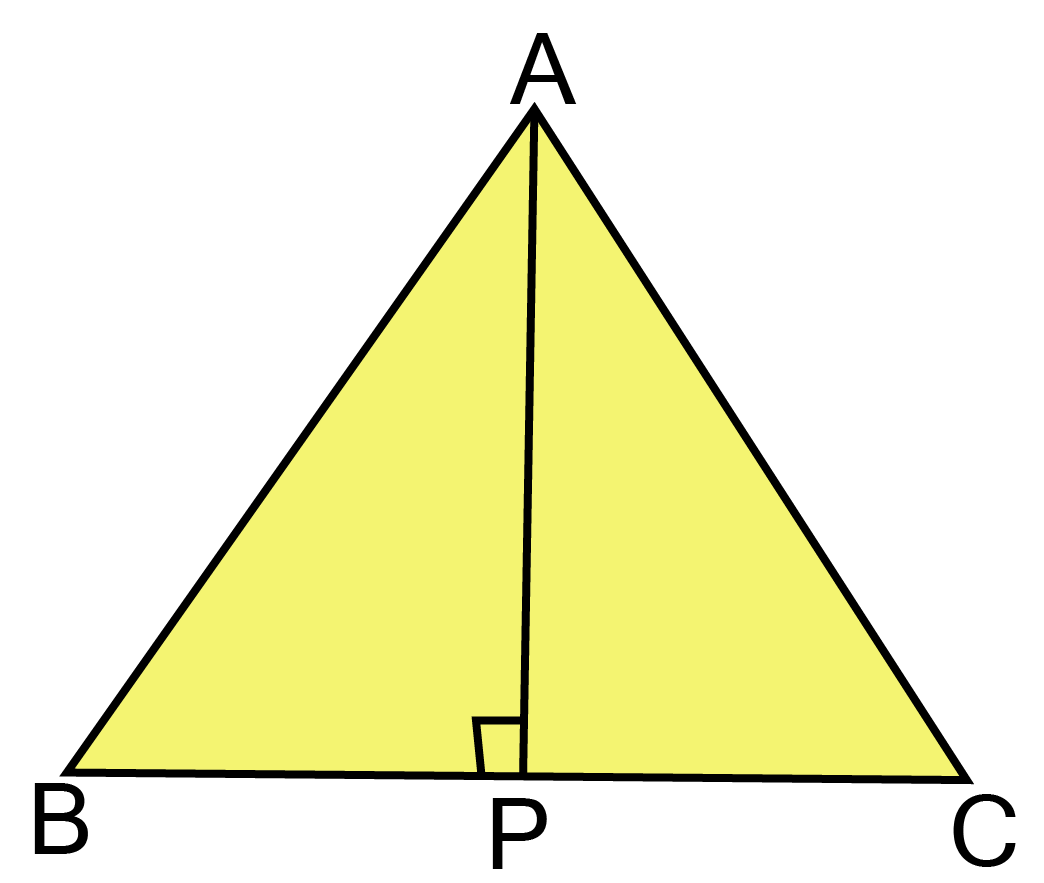
Ans: Given: ABC is an isosceles triangle in which AB = AC

${\text{Toprove:}}\angle {\text{B = }}\angle {\text{C}}  $

${\text{Construction:Draw}} {\text{AP = BC}}  $

${\text{Proof:In }}\vartriangle {\text{ABP and}} \vartriangle {\text{ACP}}  $

$\angle {\text{APB}} = \angle {\text{APC}} = {90^\circ }             [{\text{By}} {\text{construction}})  $

${\text{AB}} = {\text{AC[Given}}]  $

${\text{AP}} = {\text{AP      [Common}}]  $ 

 $\therefore \vartriangle {\text{ABP}} \cong \vartriangle {\text{ACP         [RHS congruency]}}$

$\Rightarrow \angle B = \angle C           [{\text{by CPCT}}]  $ 

 7. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (See figure). Show that $\angle $A >$\angle $ C and$\angle $ B > $\angle $D.

Ans: Given: ABCD is a quadrilateral with AB as smallest and CD as longest side.

(i). $\angle A < \angle C$

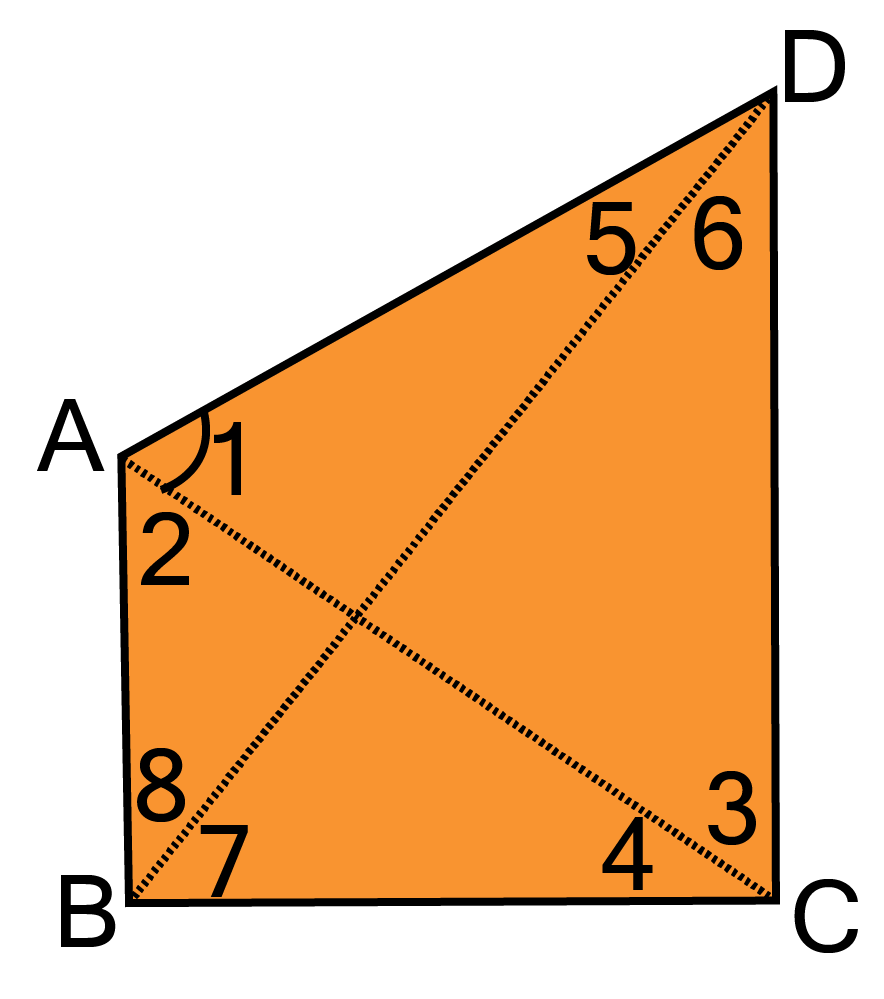
${\text{Construction: Join AC and BD}}  $

${\text{Proof:(i)In }}\vartriangle {\text{ABC,AB is the smallest side}}{\text{.}}  $

$\angle {\text{4 < }}\angle {\text{2}}...........{\text{(i)}}  $

${\text{[Angle opposite to smaller side is smaller]}}  $

${\text{In }}\vartriangle {\text{ADC, DC is the longest side}}{\text{.}}  $

$\angle {\text{3 < }}\angle {\text{1}}...........{\text{(ii)}}  $ 

${\text{[Angle opposite to longer side is longer]}}  $

${\text{Adding eq}}{\text{.(i) and (ii),}}  $

$\angle {\text{4 + }}\angle {\text{3 < }}\angle {\text{1 + }}\angle {\text{2}}  $ 

(ii). $\angle B > \angle D$

${\text{In }}\vartriangle {\text{ABD, AB is the smallest side}}{\text{.}}  $

$\therefore \angle {\text{5 < }}\angle {\text{8}}........{\text{(iii)}}  $

${\text{[Angle opposite to smaller side is smaller]}}  $

${\text{In }}\vartriangle {\text{BDC, DC is the longest side}}{\text{.}}  $

$\angle {\text{6 < }}\angle {\text{7}}..........{\text{(iv)}}  $

${\text{[Angle opposite to longer side is longer]}}  $

${\text{Adding eq}}{\text{.(iii) and (iv),}}  $

$\angle {\text{5 + }}\angle {\text{6 < }}\angle {\text{7 + }}\angle {\text{8}}  $

$\Rightarrow \angle {\text{D < }}\angle {\text{B}}  $ 

8. In figure, PR > PQ and PS bisects QPR. Prove that PSR> PSQ.

Ans:

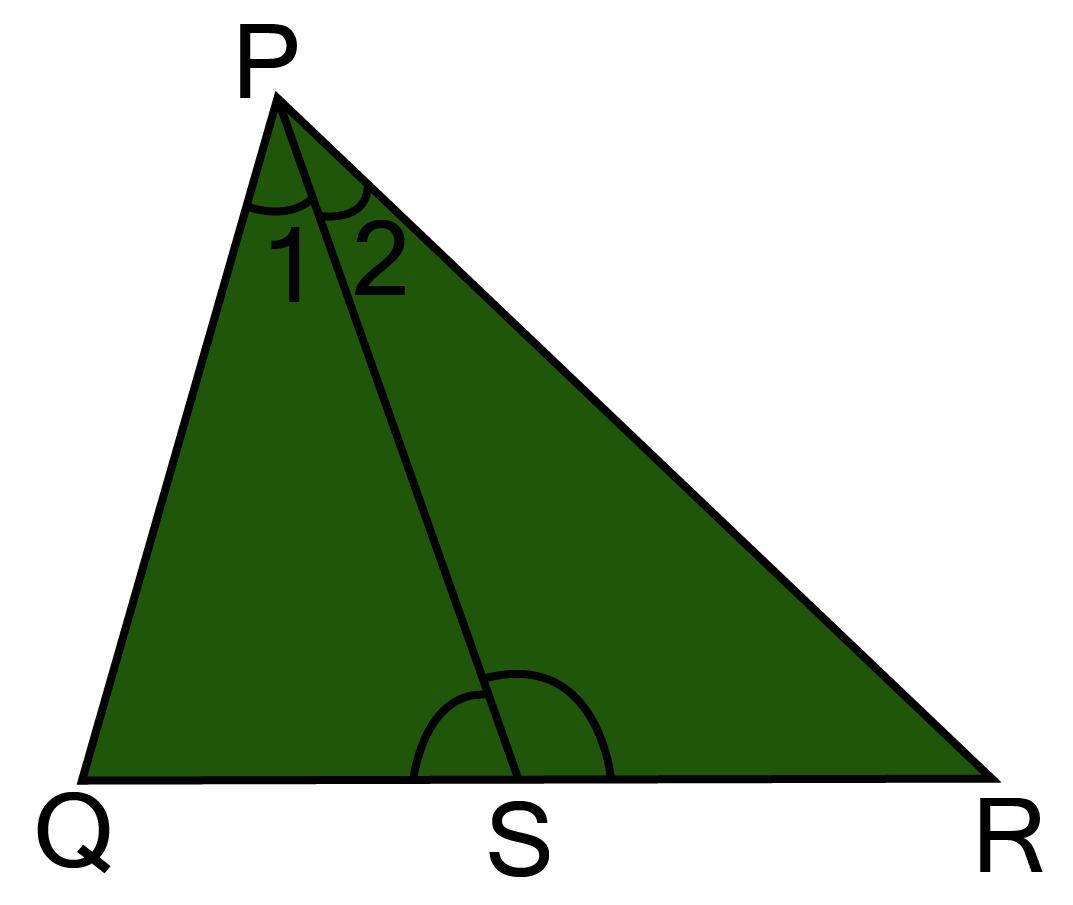
Ans: ${\text{In }}\vartriangle {\text{POR}},  $

${\text{PR}} > {\text{PQ}}[G{\text{iven}}]  $

$\therefore \angle {\text{PQR}} > \angle {\text{PR}}{{\text{Q}}_{ -  \ldots }}({\text{i}})[{\text{Angle opposite to longer side is greater}}]  $

${\text{Again }}\angle 1 = \angle 2 \ldots ({\text{ii}})  $

$\because PS{\text{ is the bisector of }}\angle P]  $

$\therefore \angle {\text{PQR}} + \angle 1 > \angle {\text{PRQ}} + \angle 2 \ldots  \ldots  \ldots ({\text{iii}})  $

But $\angle PQS + \angle 1 + \angle PSQ = \angle PRS + \angle 2 + \angle PSR = {180^\circ }  $

${\text{[Angle sum property]}}  $ 

$\Rightarrow \angle {\text{PQR}} + \angle 1 + \angle {\text{PSQ}} = \angle {\text{PRQ}} + \angle 2 + \angle {\text{PSR}} \ldots  \ldots ({\text{iv}})  $

$[\angle {\text{PRS}} = \angle {\text{PRQ and }}\angle {\text{PQS}} = \angle {\text{PQR}}]  $

From eq.(iii) and (iv),  

$\angle {\text{PSQ}} < \angle {\text{PSR}}  $

${\text{ Or }}\angle {\text{PSR}} > \angle {\text{PSQ}}  $ 

9. Show that all the line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Ans: 

Given: l is a line and P is point not lying on I.

${\text{PM}} \bot {\text{I}}  $

${\text{N is any point on other than M}}{\text{.}}  $

${\text{Proof:In}} \Delta PMN,  $

$\angle {\text{M is the right angle}}{\text{.}}  $

$\therefore {\text{N is an acute angle}}{\text{.(Angle sum property of }}\Delta)  $

$\therefore \angle {\text{M > }}\angle {\text{N}}  $

$\therefore {\text{PN > PM[Side opposite greater angle]}}  $

$\Rightarrow {\text{PM < PN}}  $ 

Hence of all line segments drawn from a given point not on it, the perpendicular is the

Shortest.

10. ABC is a triangle. Locate a point in the interior of $\vartriangle ABC$ which is equidistant from all the vertices of$\vartriangle ABC$.

Ans: Let ABC be a triangle.

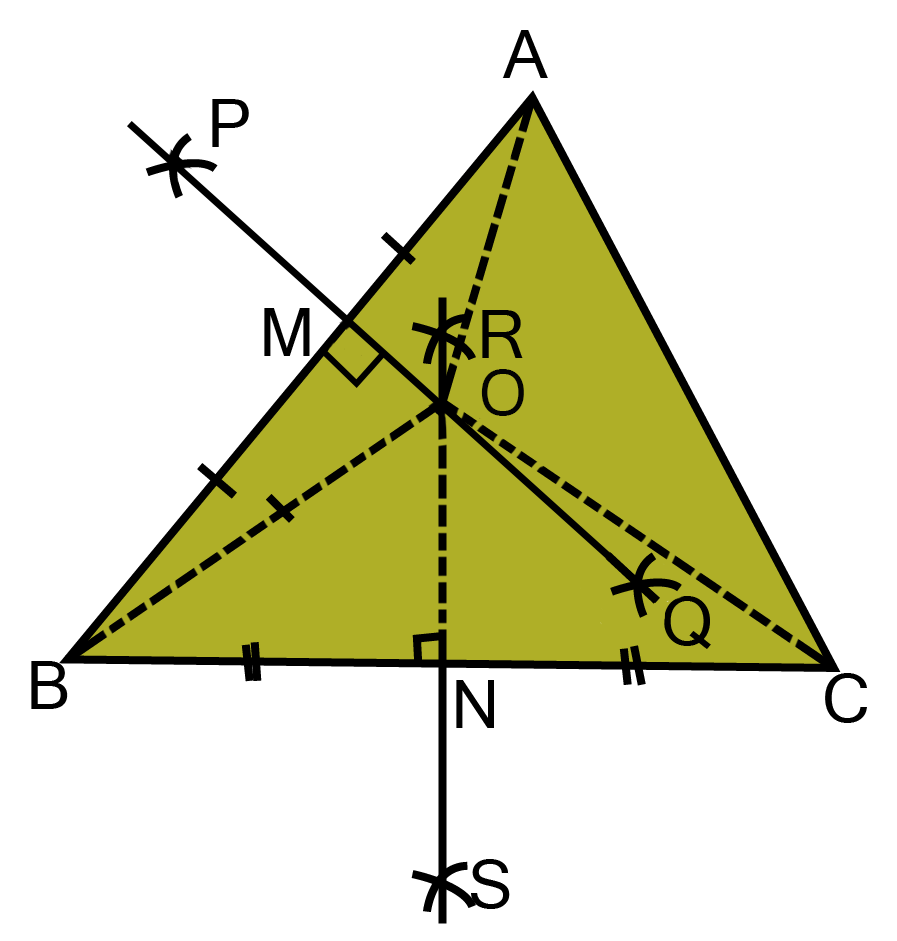
Draw perpendicular bisectors PQ and RS of sides AB and BC respectively of triangle ABC. Let PQ bisects AB at M and RS bisects BC at point N.

Let PQ and RS intersect at point O.

Join OA, OB and OC.

Now in AOM and BOM,

AM = MB               [By construction]

$\angle {\text{AMO = }}\angle {\text{BMO = 9}}{\text{0}}^\circ {\text{                [Byconstruction]}}  $

${\text{OM = OM[Common]}}  $

$\therefore \Delta {\text{ AOM}} \cong \Delta {\text{BOM               [By SAScongruency]}}  $

$\Rightarrow {\text{OA = OB[By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{. ] }}............{\text{(i)}}  $

$Similarly \Delta BON \cong \Delta CON  $

$\Rightarrow {\text{OB = OC[By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.]}}.....{\text{(ii)}}  $

${\text{From eq}}{\text{.(i)and(ii),}}  $

${\text{OA = OB = OC}}  $ 

Hence O, the point of intersection of perpendicular bisectors of any two sides of $\vartriangle ABC$equidistant from its vertices.

11. In a huge park, people are concentrated at three points (See figure).

A: where there are different slides and swings for children.

B: near which a man-made lake is situated.

C: which is near to a large parking and exit.

Where should an ice cream parlour be set up so that maximum number of persons can approach it?

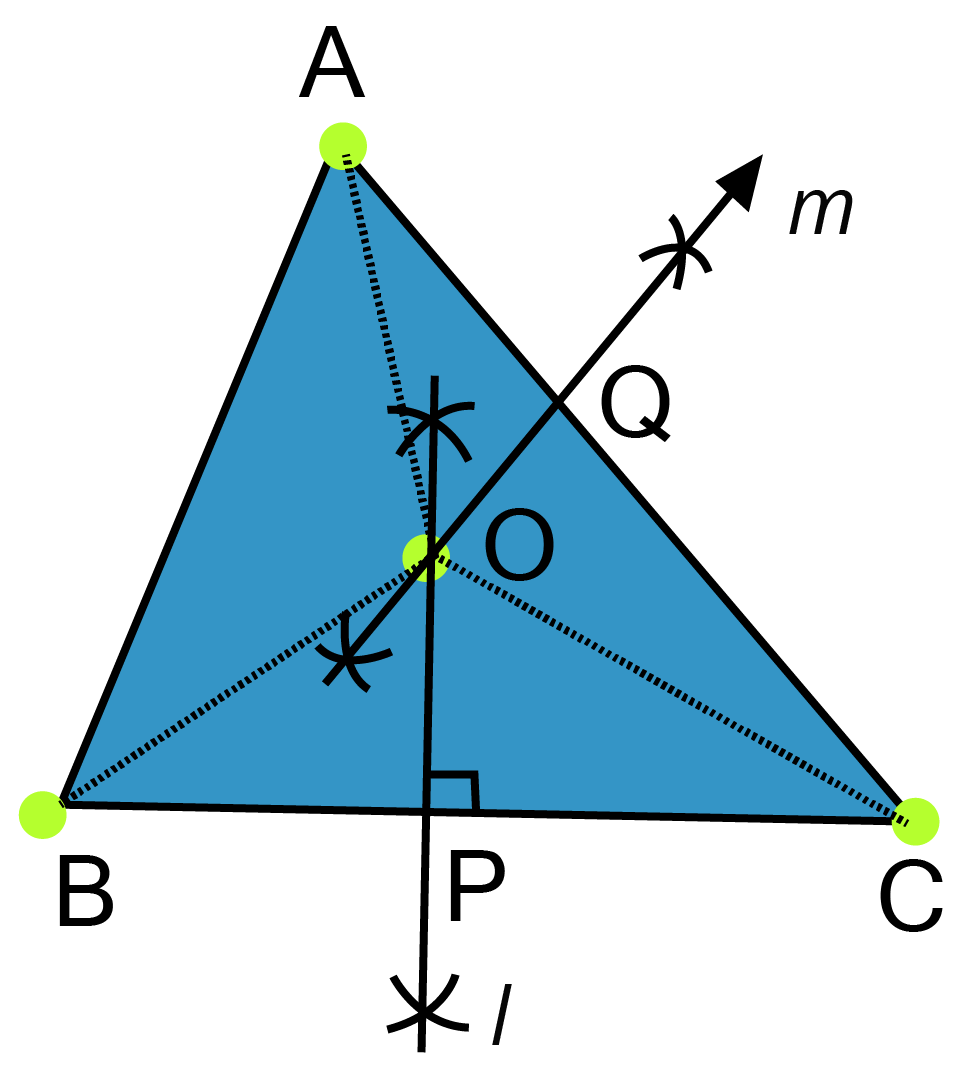
Ans: The parlour should be equidistant from A, B and C.

For this let we draw perpendicular bisector say l of line joining points B and C also draw

perpendicular bisector say m of line joining points A and C.

Let l and m intersect each other at point O.

Now point O is equidistant from points A, B and C.

Join OA, OB and OC.

Proof: in ${\Delta\text{ BOP and} \Delta COP}$,

${\text{OP = OP            [Common]}}$

$\angle {\text{OPB = }}\angle {\text{OPC = 9}}{\text{0}}^\circ {\text{                  [By construction]}}  $

${\text{BP = PC               [midpoint of BC]}}  $

$\therefore {\text{\Delta BOP}} \cong {\text{\Delta COP         [By SAScongruency]}}  $

$\Rightarrow {\text{OB = OC[By C}}{\text{.P}}{\text{.C}}{\text{.T}}.........{\text{(i)}}  $

$Similarly \Delta AOQ \cong Delta COQ  $

 $\Rightarrow {\text{OA = OC[By C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.]}}.....{\text{(ii)}}  $

${\text{From eq}}{\text{.(i)and(ii),}}  $

${\text{OA = OB = OC}}  $ 

Therefore, ice cream parlour should be set up at point O, the point of intersection of perpendicular bisectors of any two sides out of three formed by joining these points.

12. If ABC, the bisector of ABC and BCA intersect each other at the point O prove that${\text{ }}\angle {\text{BOC = 9}}{{\text{0}}^\circ }{\text{ + }}\dfrac{{\angle {\text{A}}}}{{\text{2}}}$

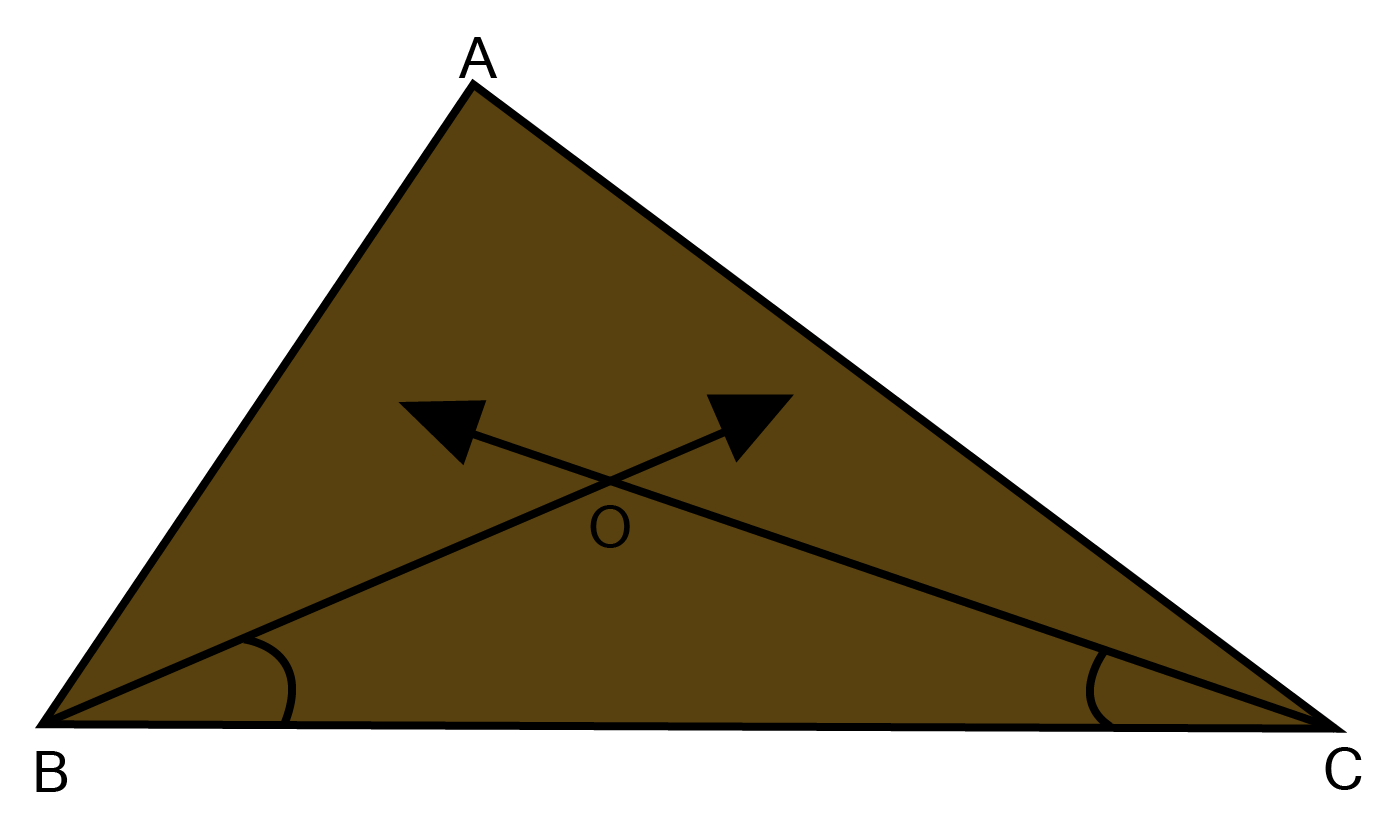
Ans: In $\vartriangle {\text{BOC}}$, we know,

$\angle {\text{1 + }}\angle {\text{2 + }}\angle {\text{BOC = 18}}{\text{0}}^\circ .....{\text{(l)}}  $

${\text{In }}\vartriangle {\text{ABC,we have }}  $

$\angle {\text{A + }}\angle {\text{B + }}\angle {\text{C = 18}}{{\text{0}}^\circ}  $

  $ \Rightarrow \angle {\text{A + 2(}}\angle {\text{1) + 2(}}\angle {\text{2) = 18}}{{\text{0}}^\circ}  $

   $\Rightarrow \dfrac{{\angle {\text{A}}}}{{\text{2}}}{\text{ + }}\angle {\text{1 + }}\angle {\text{2 = 9}}{{\text{0}}^\circ}  $

   $\Rightarrow \angle {\text{1 + }}\angle {\text{2 = 9}}{{\text{0}}^0}{\text{ - }}\dfrac{{\angle {\text{A}}}}{{\text{2}}}  $

  ${\text{ Substituting this value of }}\angle {\text{1 + }}\angle {\text{2 in (1) }}  $

  ${\text{9}}{{\text{0}}^\circ}{\text{ - }}\dfrac{{\angle {\text{A}}}}{{\text{2}}}{\text{ + }}\angle {\text{BOC = 18}}{{\text{0}}^\circ}  $

  $\angle {\text{BOC = 9}}{{\text{0}}^\circ}{\text{ + }}\dfrac{{\angle {\text{A}}}}{{\text{2}}}  $

${\text{So, }}\angle {\text{BOC = 9}}{{\text{0}}^\circ}{\text{ + }}\dfrac{{\angle {\text{A}}}}{{\text{2}}}  $ 

13. Prove that if one angle of a triangle is equal to the sum of the other two angles, the triangle is right angled

Ans:  $\angle {\text{A + }}\angle {\text{B + }}\angle {\text{C = 18}}{{\text{0}}^\circ}{\text{[Sum of three angles of triangle is}}\left. {{\text{18}}{{\text{0}}^\circ}} \right]......{\text{(1)}}  $

${\text{Given that:}}\angle {\text{A + }}\angle {\text{C = }}\angle {\text{B}}....{\text{(2)}}  $

${\text{From(1)and(2),}}  $

$\angle {\text{B + }}\angle {\text{B = 18}}{{\text{0}}^\circ}  $

 $  \Rightarrow \angle {\text{B = }}\dfrac{{{\text{18}}{{\text{0}}^\circ}}}{{\text{2}}}{\text{ = 9}}{{\text{0}}^\circ}  $

 $Hence \Delta ABC {\text{is right angled}}{\text{.}}  $ 

14. If fig, if PQ$ \bot $ PS, PQ $ \bot $SR, $\angle $SQR = ${28^0}$and $\angle $QRT =${65^0}$ , then find the values of X and Y.

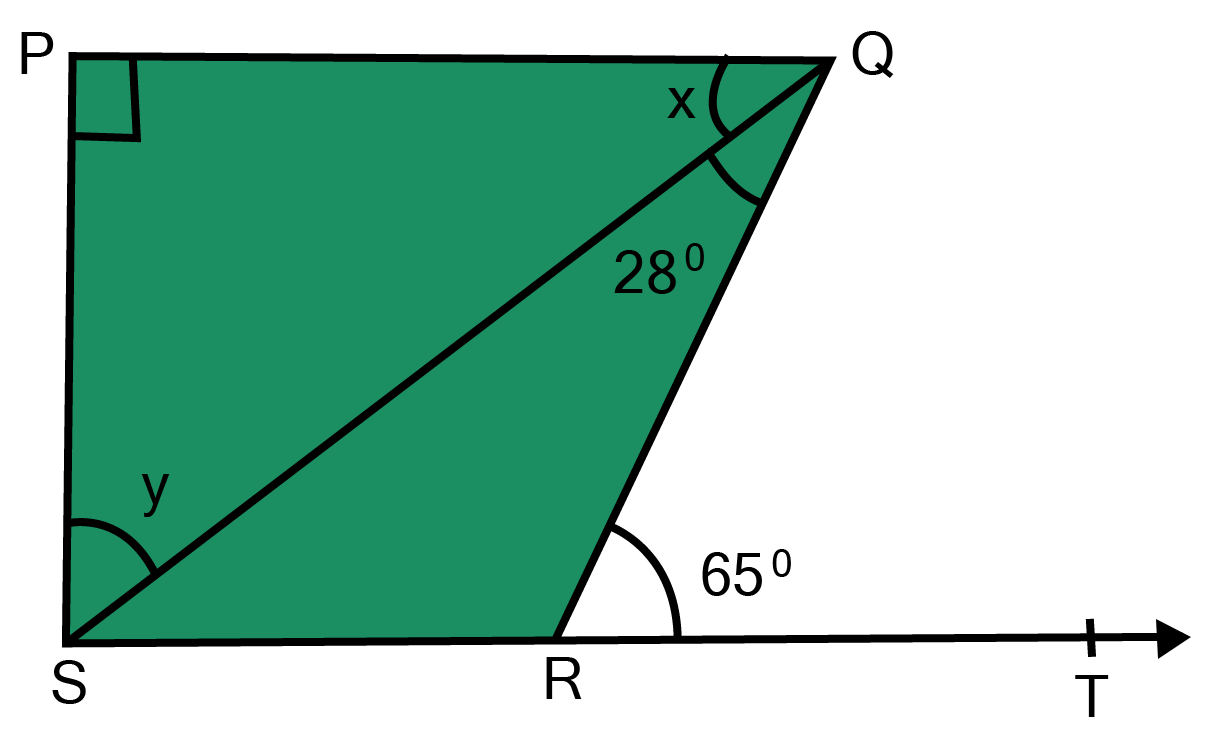
Ans: $PQ\parallel SR{\text{ and QR is the transversal,}}$

$\therefore \angle {\text{PQR = }}\angle {\text{QRT [pair of  alternate angles]}}  $

${\text{or}}\angle {\text{PQS + }}\angle {\text{SQR = }}\angle {\text{QRT }}  $

${\text{or x + 2}}{{\text{8}}^\circ}{\text{ = 6}}{{\text{5}}^\circ}$

${\text{x = 6}}{{\text{5}}^\circ}{\text{ - 2}}{{\text{8}}^\circ}{\text{ = 3}}{{\text{7}}^\circ}  $

${\text{Also in} \Delta PQS,}  $

$\angle {\text{SPQ + }}\angle {\text{PSQ + }}\angle {\text{PQS = 18}}{{\text{0}}^\circ}  $

 $\Rightarrow {\text{9}}{{\text{0}}^\circ}{\text{ + y + x = 18}}{{\text{0}}^\circ}  $

${\text{or 9}}{{\text{0}}^\circ}{\text{ + y + 3}}{{\text{7}}^\circ}{\text{ = 18}}{{\text{0}}^\circ}  $

${\text{y = 5}}{{\text{3}}^\circ}  $ 

15. If  AD= AE and D and E are point on BC such that BD=EC prove that AB=AC.

Ans: In $\vartriangle ADE$,

${\text{AD}} = {\text{AE}}[Given]  $

$\therefore \angle {\text{ADE}} = \angle {\text{AED}}[{\text{angles opposite to equal side are equal}}]  $

Now, $\angle {\text{ADE}} + \angle {\text{ADB}} = {180^\circ }[linearpair]  $

Also, $\angle {\text{AED}} + \angle {\text{AEC}} = {180^\circ }[linearpair]  $

$\Rightarrow \angle {\text{ADE}} + \angle {\text{ADB}} = \angle {\text{AED}} + \angle {\text{AEC}}  $

But, $\angle {\text{ADE}} = \angle {\text{AED}}  $

Now in, $\Delta {\text{ABD }}and{\text{ }}\vartriangle {\text{ACE}},  $

$BD = CE  $

${\text{AD}} = {\text{AE}}  $

$\angle ADB = \angle AEC  $

$\therefore \vartriangle ABC \cong \vartriangle ACE[BySAS]  $

$\Rightarrow {\text{AB}} = {\text{AC}}[{\text{CPCT}}]  $ 

16. In the given figure, AC=BC, $\angle $ DCA= $\angle $ECB and $\angle $DBC=$\angle $ EAC. Prove that $\vartriangle DBC$ and $\vartriangle EAC$ are congruent and hence DC=EC.

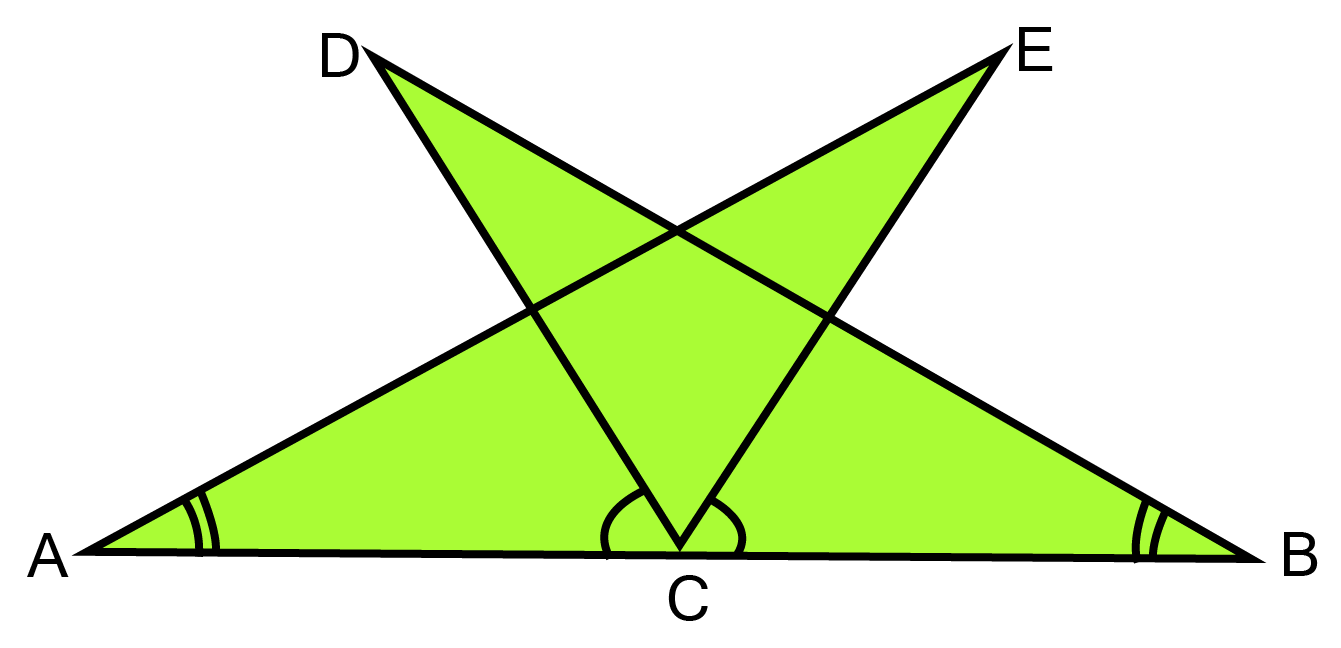
Ans: We know, 

$\angle {\text{DCA = }}\angle {\text{ECB[Given]}}  $

 $\Rightarrow \angle {\text{DCA + }}\angle {\text{ECD = }}\angle {\text{ECB + }}\angle {\text{ECD[adding  }}\angle {\text{ECD on both sides]}}  $

 $\Rightarrow \angle {\text{ECA = }}\angle {\text{DCB}}...{\text{(i) }}  $

$\angle {\text{DCB = }}\angle {\text{ECA               [From(i)]}}  $

Now in,

$\vartriangle {\text{DBC}} and \vartriangle {\text{ EAC}}$

${\text{BC = AC                [given]}}$

$\angle {\text{DBC = }}\angle {\text{EAC               [given]}}  $

$\vartriangle {\text{DBC}} \cong \vartriangle{\text{ EAC               [BySAS]}}  $

$\Rightarrow {\text{DC = EC                  [CPCT]}}  $ 

17. From the following figure, prove that $\angle BAD = 3\angle ADB$.

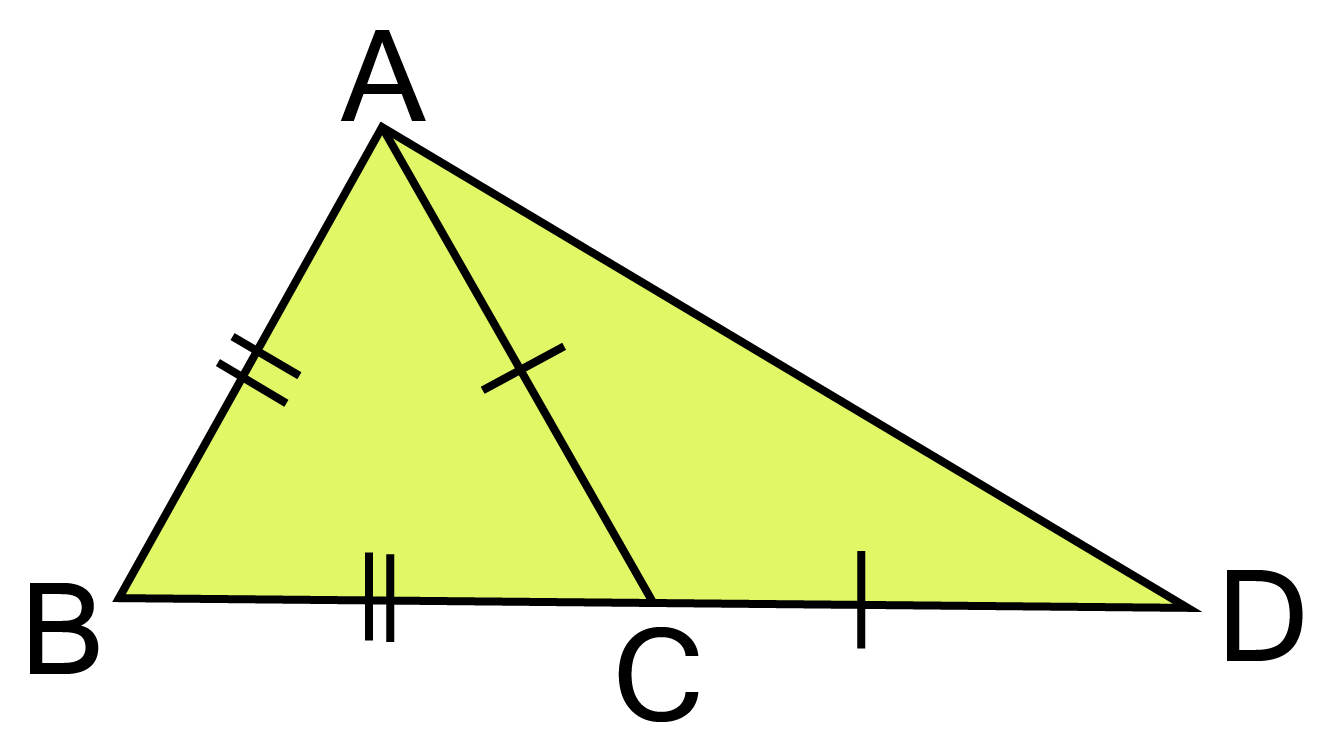
Ans: Let $\angle ADC = Q$

$\Rightarrow \angle CAD = Q[\because ,CA = CD]{\text{ }}  $

${\text{Exterior }}\angle ACB = \angle CAD = Q + Q = 2Q  $

$\Rightarrow \angle BAC = 2Q[\because BA = BC]  $

$\angle BAD = \angle BAC + \angle CAD{\text{ }}  $

$ = 2Q + Q = 3Q  $

$= 3\angle ADC = 3\angle ADB  $ 

Hence $\angle BAD = 3\angle ADB$

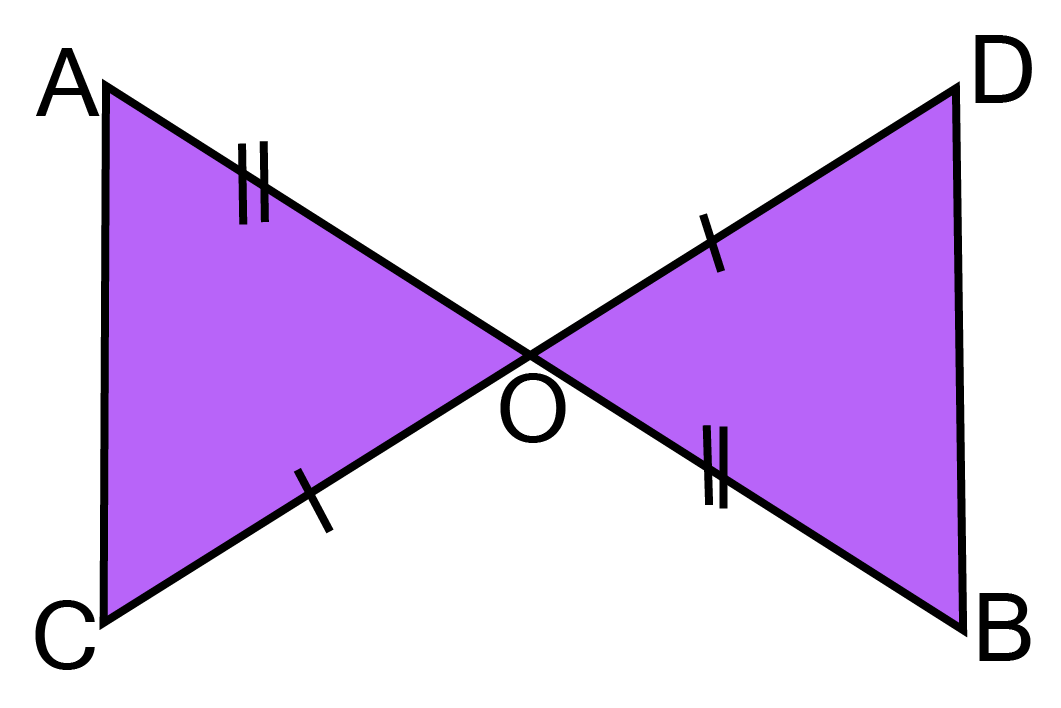
18. Is the mid-point of AB and CD. Prove that AC=BD and $AC\parallel BD$.

Ans: 

${\text{In }}\vartriangle AOC{\text{ }}and\vartriangle BOD  $

$AO = OB[{\text{O is the mid - point of AB}}]  $

$\angle AOC = \angle BOD[{\text{vertically opposite angles}}]  $

 $CO = OD[{\text{O is the mid - point of CD}}]  $

 $\vartriangle AOC \cong \vartriangle BOD[{\text{ By SAS }}]  $

 $AC = BD[{\text{CPCT}}]  $

 $\Rightarrow \angle CAO = \angle DBO[{\text{CPCT}}]  $ 

Now, AC and BD are two lines inter sected by a transversal AB such that i.e. alternate angle are equal

19. ABCD is a quadrilateral in which AD=BC and $\angle $DAB= $\angle $CBA. Prove that.

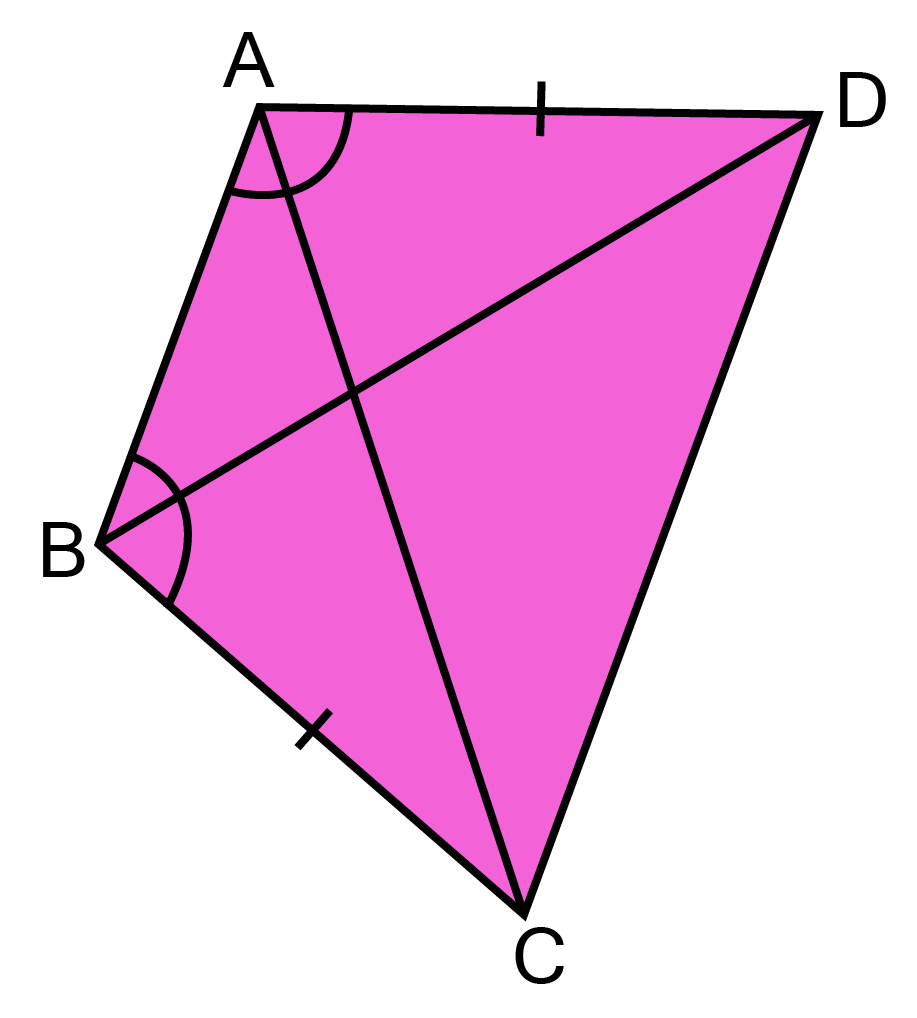
(i). $\vartriangle ABD \cong \vartriangle BAC$

Ans: 

${\text{In }}\vartriangle {\text{ABD and }}\vartriangle {\text{BAC,}}  $

${\text{AD = BC[given]}}  $

$\angle {\text{DAB}} = \angle {\text{CBA[given]}}  $

${\text{AB = AB[Common]}}  $

 because $\vartriangle {\text{ABD}} \cong {\text{ }}\vartriangle {\text{BAC[SAS criterion]}} $ 

(ii). $BD = AC$

Ans: $BD = AC$[by CPCT] 

(iii). $\angle ABD = \angle BAC$

Ans: In reference with the first part 

$\angle ABD = \angle BAC$

20. AB is a line segment. AX and BY are equal two equal line segments drawn on

opposite side of line AB such that $AX\parallel BY$. If AB and XY intersect each other at P. prove that

(i). $\vartriangle APX \cong \vartriangle BPY$

Ans: In $\vartriangle APX{\text{ and }}\vartriangle BPY$,

$\angle X  = \angle Y{\text{                 [alternate angle]}}  $

$\angle APX = \angle BPY{\text{      [ vertically opposite angle]}}  $

AX = BY               [given]  

$\therefore \Delta APX \cong \vartriangle BPY[ByAAS]  $ 

(ii). AB and XY bisect each other at P.

Ans: $ AX = BY[given]$

$\therefore \Delta APX \cong \vartriangle BPY[ByAAS]  $

$\Rightarrow AP = BP{\text{ }}and{\text{ }}PX = PY[{\text{CPCT}}]  $

$ \Rightarrow {\text{AB and XY bisects each other at P}}  $

21. In an isosceles $\vartriangle ABC$, with AB =AC, the bisector of $\angle $B and $\angle $C intersect each  other at O, join A to O. show that:

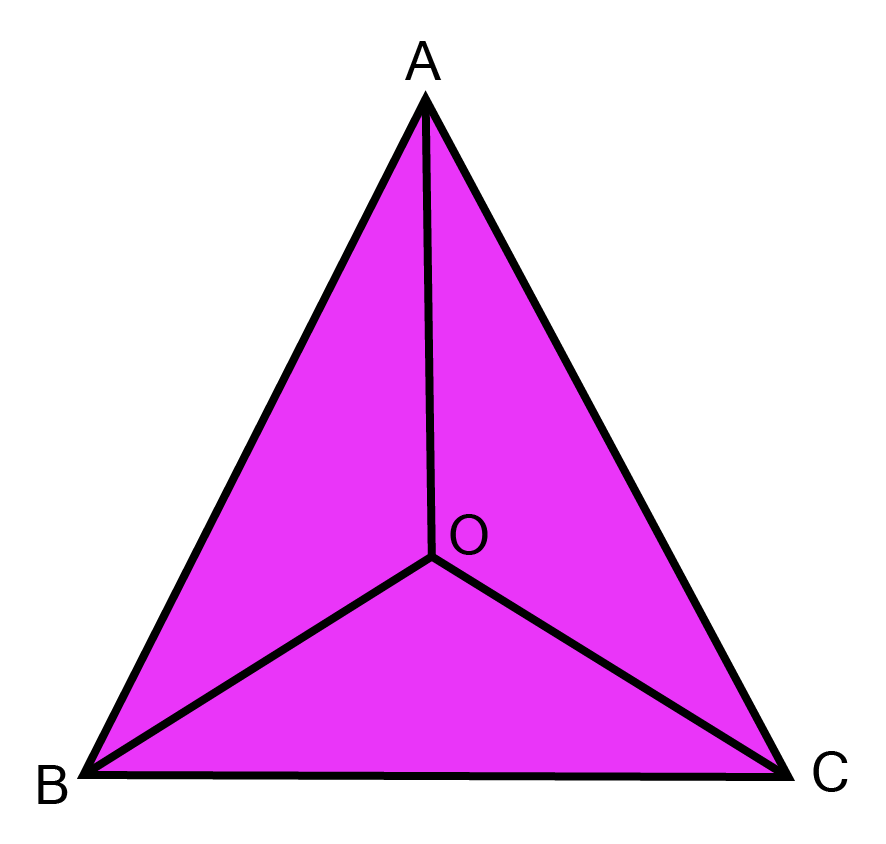
(i). OB=OC

Ans: ${\text{In }}\Delta {\text{ABC}}$

${\text{AB}} = {\text{AC}}[{\text{given}}]  $

$\angle {\text{ACB}} = \angle {\text{ABC}}[{\text{angles opposite to equal side}}]  $

$\therefore \dfrac{1}{2}\angle {\text{ACB}} = \dfrac{1}{2}\angle {\text{ABC }}  $

${\text{or }}\angle {\text{OCB}} = \angle {\text{OBC}}  $

$\Rightarrow {\text{OB}} = {\text{OC}}[{\text{  side opposite to equal angle}}]  $ 

(ii). AO bisects $\angle $A.

Ans: ${\text{In }}\vartriangle AOB{\text{ and }}\Delta {\text{AOC}}$

${\text{AB}} = {\text{AC}}[{\text{        given}}]  $

$\angle {\text{ABO}} = \angle {\text{ACO}}[{\text{           Halves of equals}}]{\text{ }}  $

${\text{OB }} = {\text{OC}}[{\text{       proved}}]  $

$\therefore \vartriangle {\text{AOB}} \cong \vartriangle$ ${\text{AOC}}{\text{          [SAS rule]}}  $

 $\Rightarrow \angle {\text{BAO}} = \angle {\text{CAO}}[{\text{CPCT}}]  $

 ${\text{i}}{\text{.e}}{\text{. AO bisects }}\angle {\text{A}}  $ 

22. Two side AB and BC and median AM of a triangle ABC are respectively equal to side PQ and QR and median PN of $\vartriangle PQR$, show that

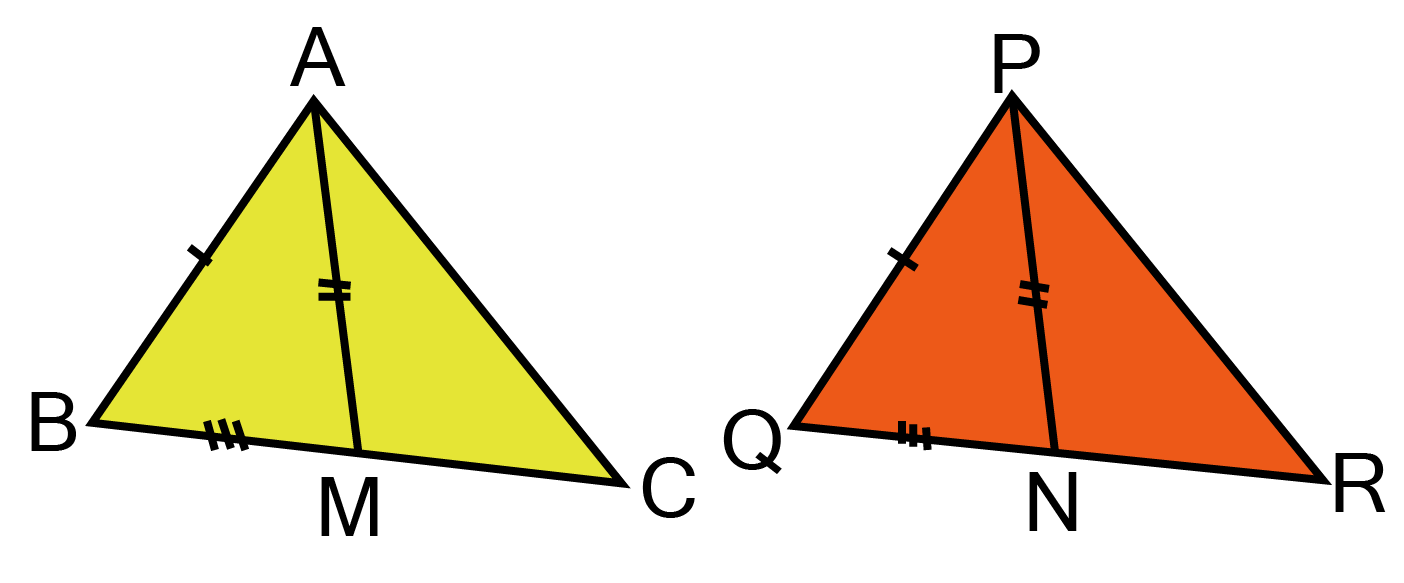
(i). $\vartriangle ABM \cong \vartriangle PQN$

Ans: $In\vartriangle {\text{ABM }}and\vartriangle {\text{PQN}}$

$AB = PQ[Given]  $

${\text{BM}} = {\text{QN}}[Halves{\text{ }}of{\text{ }}equal]  $

AP = PN[Given]  

$ \therefore \Delta {\text{ABM}} \cong \Delta {\text{PQN}}[SSS{\text{ }}rules]  $ 

(ii). $\vartriangle ABC \cong \vartriangle PQR$

$ \Rightarrow \angle {\text{B}} = \angle {\text{Q}}  $

Now, in ${\text{ }}\Delta {\text{ABC}} and {\text{PQR}}\,,  $

${\text{AB}} = {\text{PQ}}[Given]  $

  BC = QR[Given]  

$\angle {\text{B}} = \angle {\text{Q}}[Proved]  $

$\therefore \vartriangle {\text{ABC}} \cong \vartriangle {\text{PQR}}.[SASrule]  $ 

23. In the given figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that $\angle ABD = \angle ACD$,

Ans: In $\vartriangle ABC$,

${\text{AB}} = {\text{AC}}[Given]  $

$\therefore \angle {\text{ABC}} = \angle {\text{ACB}}[{\text{angles opposite to equal side are equals}}]  $

  ${\text{Similarly}} {\text{in,}}\vartriangle {\text{DBC}},  $

  ${\text{DB}} = {\text{DC}}[Given].....(1)  $

  $\therefore \angle {\text{DBC}} = \angle {\text{DCB}}  $

  ${\text{Adding(1)and(2}})  $

  $\angle {\text{ABC}} + \angle {\text{DBC}} = \angle {\text{ACB}} + \angle {\text{DCB}}   $

  or; $\angle {\text{ABD}} = \angle {\text{ACD}}  $ 

24. Prove that the Angle opposite to the greatest side of a triangle is greater than two third of a right angle i.e. greater than${60^0}$

Ans: In $\vartriangle ABC$,

$AB > BC[given]  $

$\angle C > \angle A[angle{\text{ opposite to large side is greater}}].....(i)  $

${\text{similarly,}}  $

$AB > AC  $

$\therefore \angle C > \angle B............(ii)  $ 

adding (i) and (ii),

${\text{2}}\angle C > (\angle A + \angle B)  $

${\text{adding }}\angle {\text{C to both sides,}}  $

${\text{3}}\angle {\text{C > (}}\angle {\text{A + }}\angle {\text{B + }}\angle {\text{C)}}  $

${\text{3}}\angle {\text{C > 18}}{{\text{0}}^0}[{\text{sum of three angles of a triangle is 18}}{{\text{0}}^0}]  $

        or ${\text{ }}\angle C > {60^0}  $ 

25. AD is the bisector of $\angle $A of ABC, where D lies on BC. Prove that AB>BD and

AC>CD.

Ans: In $\vartriangle ADC$

$\angle 3 > \angle 2{\text{[Exterior angles of  }}\vartriangle $ is greater than each of the interior opposite angles.

but $\angle 2 = \angle 1[AD{\text{ bisects  }}\angle A]  $

$\therefore \angle 3 = \angle 1[{\text{Side opposite to greater angle is larger]}}  $ 

$\Rightarrow {\text{AB}} > {\text{BD}}  $

In $\vartriangle {\text{ABD}}  $

$\angle 4 > \angle 1[{\text{Exterior angles of triangle  is greater than each of the interior opposite angles]}}  $

But, $\angle {\text{1}} = \angle 2  $

$\therefore \angle 4 > \angle 2  $

$\Rightarrow {\text{AC}} > {\text{CD}}[{\text{Side opposite to greater angle is larger]}}{\text{.}}  $ 

26. In the given figure, AB and CD are respectively the smallest and the largest side of a quadrilateral ABCD. Prove that $\angle $A> $\angle $C and $\angle $B>$\angle $ D.

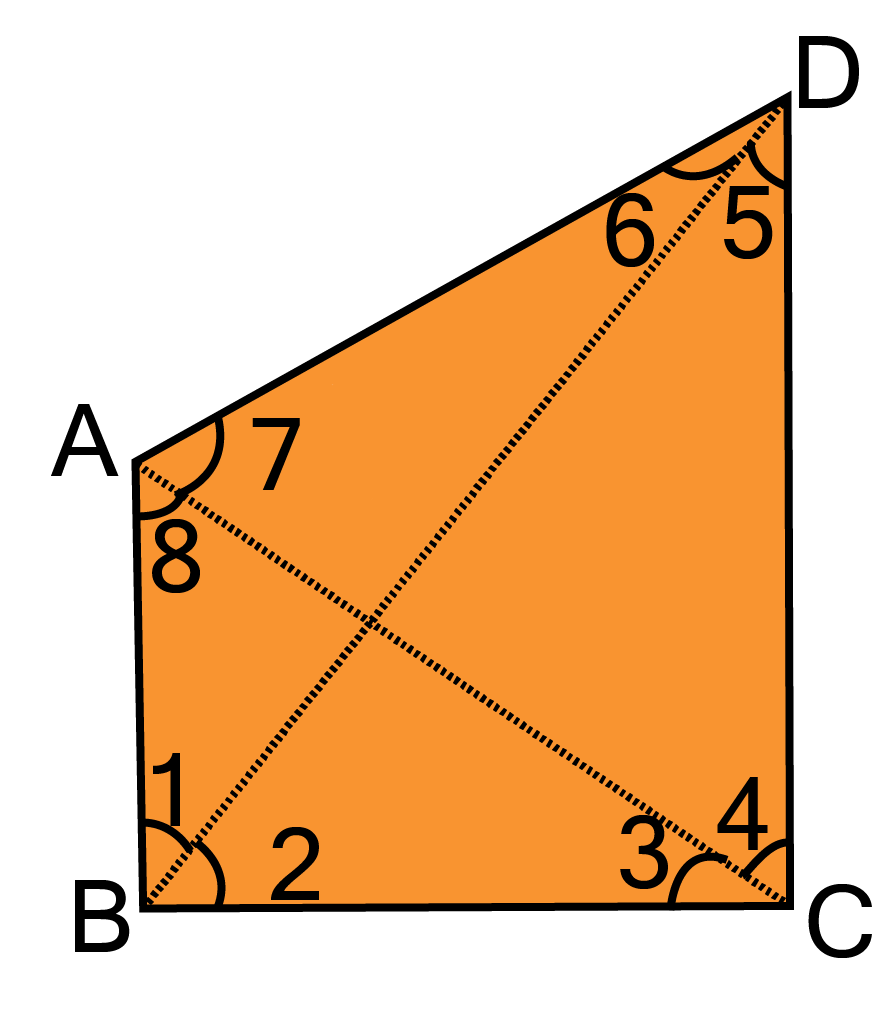
Ans: Join AC. 

In $\vartriangle {\text{ABC}}  $

${\text{BC}} > {\text{AB }}[{\text{AB is the smallest sides of quadrilateral ABCD]}}  $

$\Rightarrow \angle 8 > \angle 3[{\text{Angle opposite to larger side is greater}}]...(i)  $

In ${\text{ }}\vartriangle {\text{ADC}}  $

${\text{CD}} > {\text{AD}}[{\text{CD is the largest side of quadrilateral ABCD}}]  $

$\angle 7 > \angle 4[{\text{angle opposite to larger side is greater}}]....(ii)  $

${\text{Adding (i) and (ii) }}  $

$\angle 8 + \angle 7 > \angle 3 + \angle 4{\text{ }}  $

${\text{Or }}\angle A > \angle C  $

${\text{Similarly,by joining BD,we can show that}}\angle {\text{B}} > \angle {\text{D}}  $ 

27. If the bisector of a vertical angle of a triangle also bisects the opposite side; prove that the triangle is an isosceles triangle.

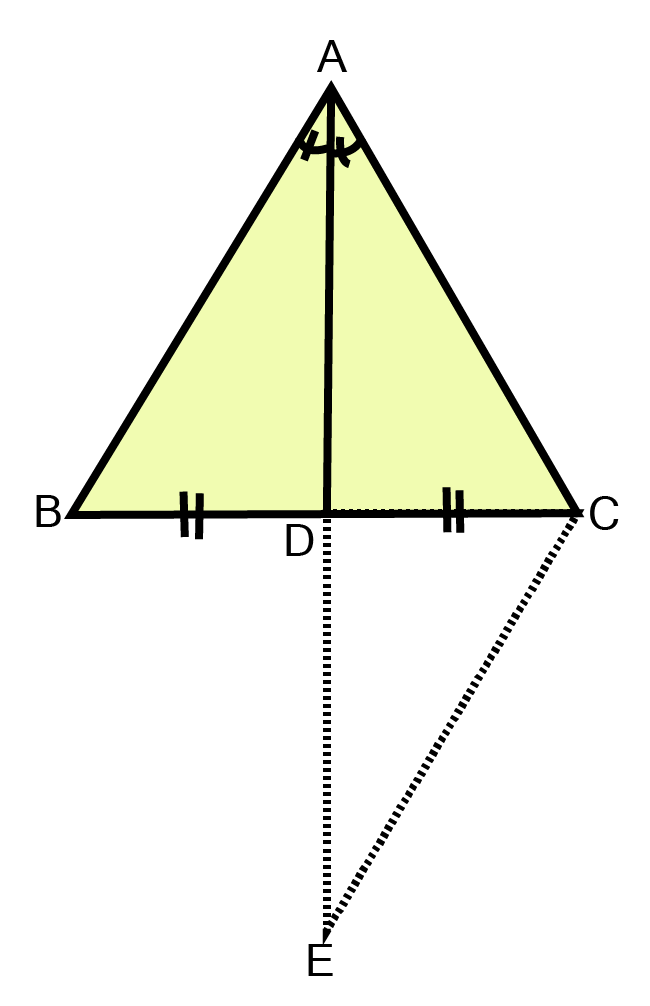
Ans: In $\vartriangle ADC{\text{ and }}\vartriangle EDB$,

$DC = DB       [{\text{Given}}]  $

$AD = ED                [{\text{By}} {\text{construction}}]  $

$\angle {\text{ADC}} = \angle {\text{EDB }}            [{\text{vertically}} {\text{opposite}} {\text{angle}}]  $

$\therefore \vartriangle {\text{ADC}} \cong \angle {\text{EDB               [BySAS]}}  $

 $\Rightarrow {\text{AC}} = {\text{EB and }}\angle {\text{DAC = }}\angle {\text{DEB                   [CPCT}}]  $

  But, $\angle {\text{DAC}} = \angle{\text{BAD}}[\because{\text{AD}}\,{\text{bisects}} \angle A]  $

$\therefore \angle {\text{BAD}} = \angle DEB  $

$\Rightarrow {\text{AB}} = {\text{BE}}  $

${\text{But}} {\text{BE = AC[Proved}} {\text{above]}}  $

$\therefore AB = AC  $ 

28. ABC is an isosceles triangle with AB = AC. Draw AP $ \bot $BC to show that $\angle B = \angle C$

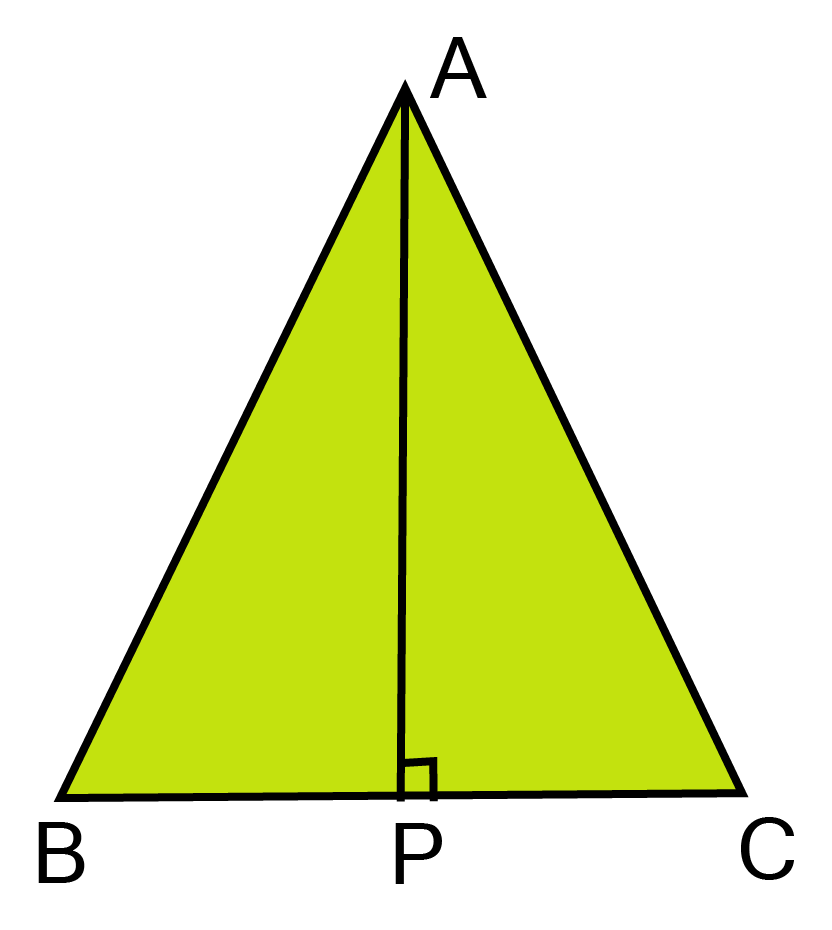
Ans: ${\text{In a right angled triangle APB and APC,}}$

${\text{AP = AP [common]}}  $

${\text{Hypotenuse AB  =  Hypotenuse AC [Given]}}  $

$\therefore \vartriangle APB \cong \vartriangle APC{\text{[RHS rule]}}  $

$\Rightarrow \angle {\text{B = }}\angle {\text{C[CPCT]}}  $ 

29. AD is an altitude of an isosceles triangle ABC in which AB = AC. Prove that:

(i). AD bisects BC

Ans: In right triangle ABD and ACD,

Side AD = Side AD            [common]

Hypotenuse AB = Hypotenuse AC      [Given]

$\therefore \vartriangle ABD \cong \vartriangle ACD[{\text{by RHS congruency}}]  $

$\Rightarrow BD{\text{  =  CD    [CPCT]}}  $

${\text{Also, AD bisects BC}}  $ 

(ii). AD bisects$\angle A$

 Ans: $\angle BAD{\text{  =  }}\angle {\text{CAD    [CPCT]}}$

 $\therefore {\text{ AD bisects }}\angle A$

30. In the given figure, PQ>PR, QS and RS are the bisectors of the $\angle $Q and $\angle $R respectively. Prove that SQ>SR.

Ans: Since PQ>PR

$\therefore \angle R > \angle {\text{Q}}[{\text{angle opposite to larger side is larger}}]  $

$\Rightarrow \dfrac{1}{2}\angle R > \dfrac{1}{2}\angle Q  $

$\Rightarrow \angle {\text{SRQ}} > \angle {\text{SQR}}  $

$\Rightarrow {\text{SQ}} > {\text{SR}}[{\text{Side opposite to greater angle is larger]}}  $ 

4 Marks Questions 

1. In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. (See figure) 

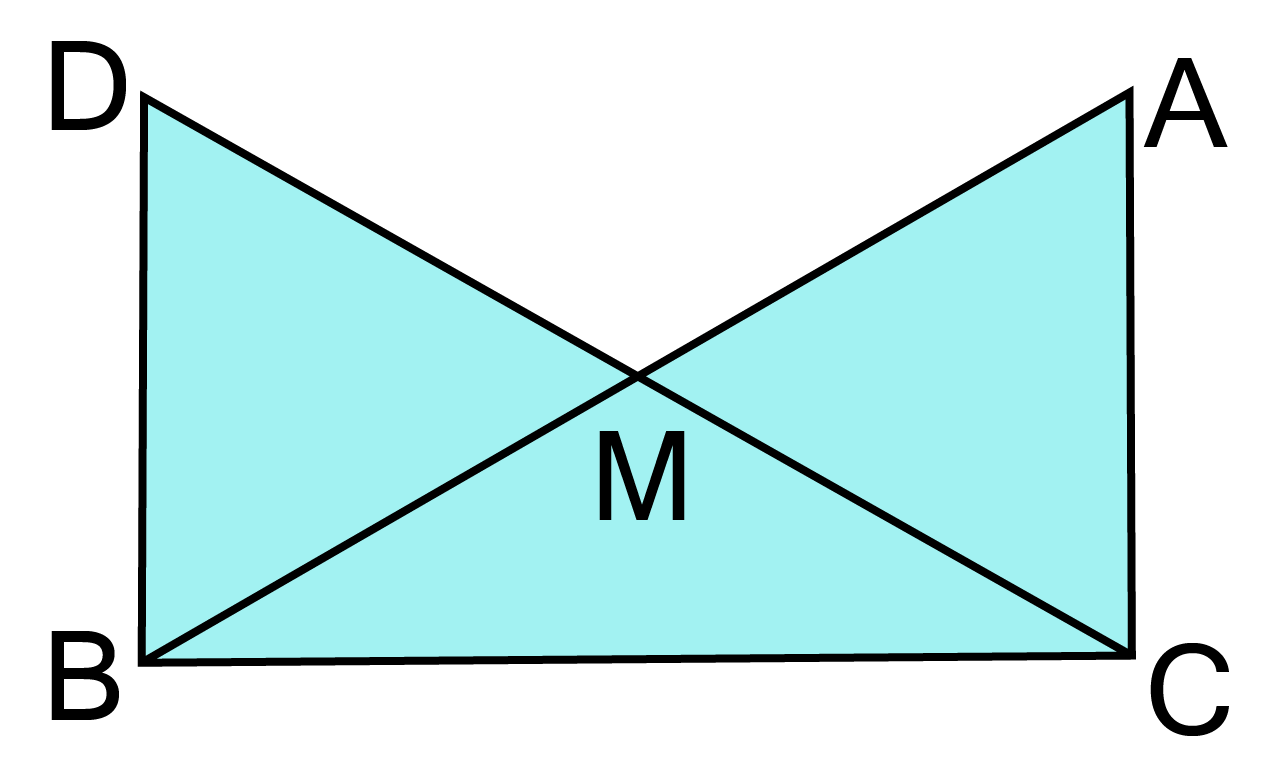
Show that:

(i) $\vartriangle {\text{AMC }} \cong {\text{ }}\vartriangle {\text{BMD}}$

Ans: ${\text{In}} \vartriangle {\text{AMC and }}\vartriangle {\text{BMD}}  $

${\text{AM = BM          [M is the mid - point of AB]}}  $

$\angle {\text{AMC = }}\angle {\text{BMD[Vertically opposite angles]}}  $

${\text{CM = DM[Given]}}  $

$\therefore \vartriangle {\text{AMC}} \cong \vartriangle {\text{BMD[By SAS congruency]}}  $

$\therefore \angle {\text{ACM = }}\angle {\text{BDM}}......{\text{(i)}}  $

$\angle {\text{CAM = }}\angle {\text{DBM and AC = BD[by C}}{\text{.P}}{\text{.C}}{\text{.T}}{\text{.]}}  $ 

(ii) DBC is a right angle. 

Ans: For two lines AC and DB and transversal DC, we have 

$ \angle ACD = \angle BDC           {\text{[Alternate angles]}} $

$\therefore AC \parallel DB $

Now, forparallel lines AC and DB and transversal DC, we have 

$ \angle DBC = \angle ACB           {\text{[Alternate angles]}}...........(ii) $

But $\vartriangle ABC$ is a right angled triangle and right angled at C.

$\therefore \angle ACB = 90^\circ  ………………..(iii)$

 Using (ii) and (iii)

$\angle DBC=90^\circ $

$\Rightarrow \angle DBC is a right angle. $

(iii) $\vartriangle {\text{DBC }} \cong {\text{ }}\vartriangle {\text{ABC}}$

Ans: ${\text{Now in }}\vartriangle {\text{DBC and }}\vartriangle {\text{ABC}}  $

${\text{DB = AC [Proved - in part(i)]}}  $

$\angle {\text{DBC = }}\angle {\text{ACB = 90}}^\circ {\text{ [Proved in part (ii)]}}  $

${\text{BC = BC [Common]}}  $

$\therefore \vartriangle {\text{DBC}} \cong \vartriangle {\text{ACB [By SAS congruency]}}$ 

(iv) $ {\text{CM}} = \dfrac{1}{2}{\text{AB}} $ 

Ans: ${\text{Since}} \Delta {\text{DBC}} \cong \vartriangle {\text{ACB }}[{\text{Proved}} {\text{above}}]  $

${\therefore {\text{DC}} = {\text{AB}}} $ 

${ \Rightarrow {\text{AM}} + {\text{CM}} = {\text{AB}}} $ 

${ \Rightarrow {\text{CM}} + {\text{CM}} = {\text{AB }}[\because {\text{DM}} = {\text{CM}}]} $ 

${ \Rightarrow 2{\text{CM}} = {\text{AB}}} $ 

${ \Rightarrow {\text{CM}} = \dfrac{1}{2}{\text{AB}}} $ 

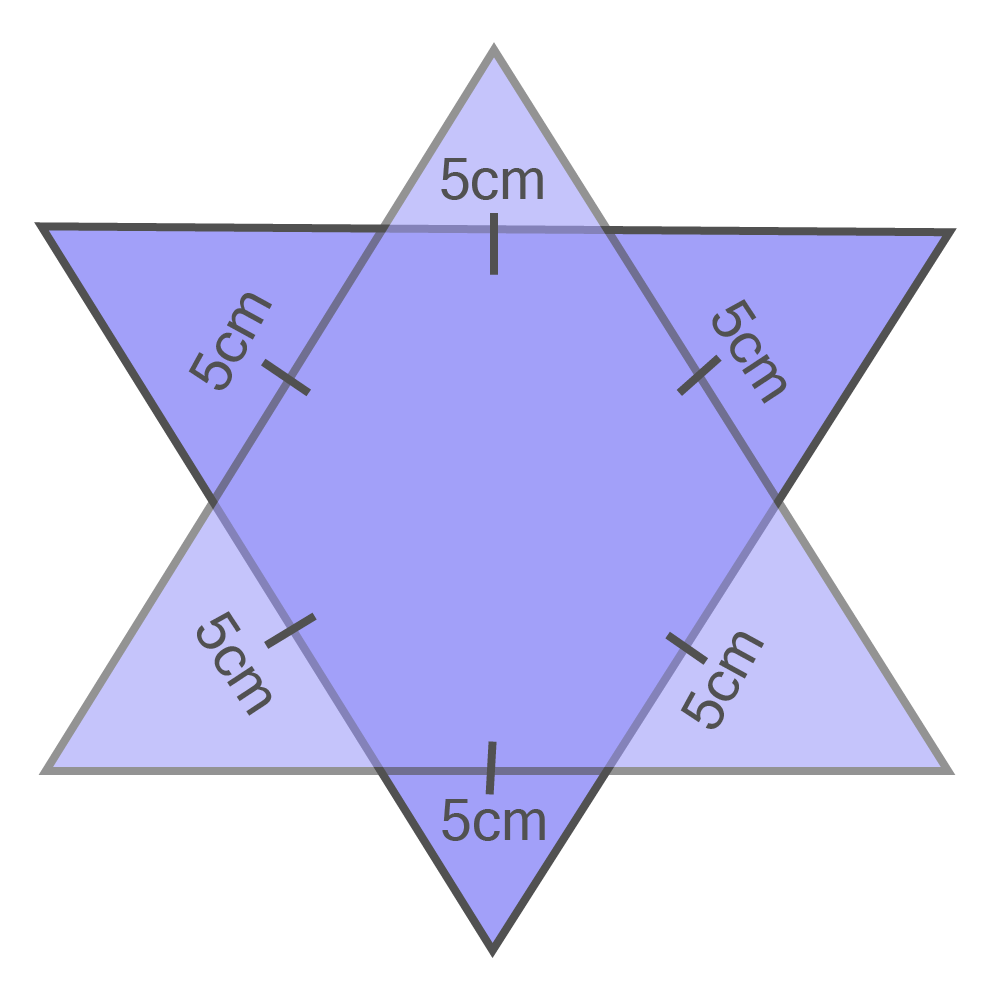
2. Complete the hexagonal rangoli and the star rangoli (See figure) but filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

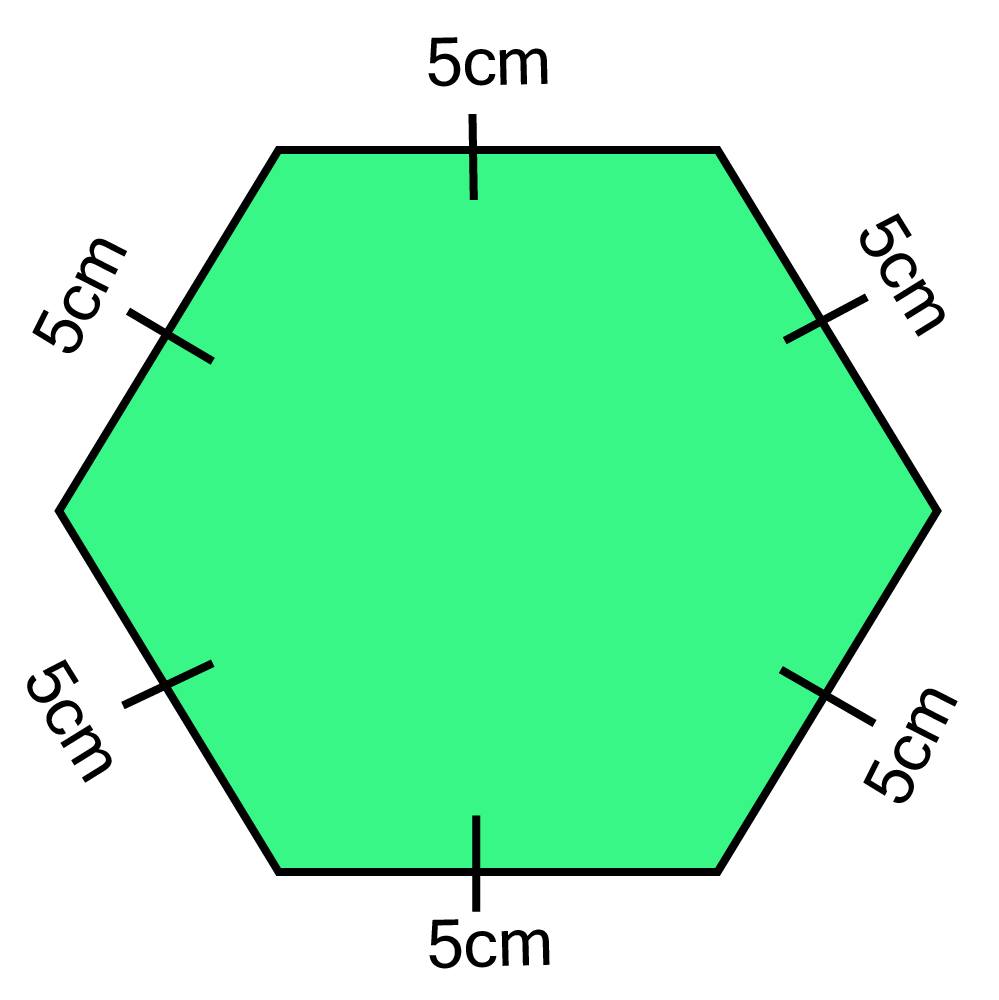
Ans: In hexagonal rangoli, Number of equilateral triangles each of side 5 cm are 6.

Area of equilateral triangle =$\dfrac{{\sqrt 3 }}{4}{({\text{ side }})^2} = \dfrac{{\sqrt 3 }}{4}{(5)^2} = \dfrac{{\sqrt 3 }}{4} \times 25{\text{ sq}}{\text{. cm}}$ 

Area of hexagonal rangoli = 6 x Area of an equilateral triangle

$ = 6 \times \dfrac{{\sqrt 3 }}{4} \times 25 = 150 \times \dfrac{{\sqrt 3 }}{4}{\text{sq}} \cdot {\text{cm}} \ldots  \ldots $ (1)

Now area of equilateral triangle of side 1 cm= $\dfrac{{\sqrt 3 }}{4}{({\text{ side }})^2} = \dfrac{{\sqrt 3 }}{4}{(1)^2} = \dfrac{{\sqrt 3 }}{4}{\text{ sq}}{\text{. cm}}{\text{. }}$ ...(2)

Number of equilateral triangles each of side 1 cm in hexagonal rangoli

$ = 150 \times \dfrac{{\sqrt 3 }}{4} + \dfrac{{\sqrt 3 }}{4} = 150 \times \dfrac{{\sqrt 3 }}{4} \times \dfrac{4}{{\sqrt 3 }} = 150 \ldots .(3)$ 

Now in Star rangoli,

Number of equilateral triangles each of side ${\text{5cm}}$ = ${\text{12}}$

Therefore, total area of star rangoli = ${\text{12 ( Area of an equilateral triangle of side 5cm)}}$

${ = 12 \times \left( {\dfrac{{\sqrt 3 }}{4}{{(5)}^2}} \right)} $ 

${ = 12 \times \dfrac{{\sqrt 3 }}{4} \times 25} $ 

${ = 300\dfrac{{\sqrt 3 }}{4}sq,c{m_ \cdots } \ldots  \ldots .(iv)} $

Number of equilateral triangles each of side 1 cm in star rangoli

$ { = 300\dfrac{{\sqrt 3 }}{4} \div \dfrac{{\sqrt 3 }}{4}} $ 

${ = 300\dfrac{{\sqrt 3 }}{4} \times \dfrac{4}{{\sqrt 3 }}} $ 

${ = 300 \ldots  \ldots .(v)} $

From eq. (iii) and (v), we observe that star rangoli has more equilateral triangles each of side=1 cm

3. Prove that the sum of the quadrilateral is ${\text{36}}{{\text{0}}^0}$ ?

Ans:

${\text{Join B and D}}  $

${\text{to obtain two triangles ABD and BCD}}  $

$\angle {\text{BAD}} + \angle {\text{ABD}} + \angle {\text{BDA}} = {180^\circ }[{\text{sum of three angles of }} \Delta  is 180^\circ].....(1)  $

$\angle {\text{CBD + }}\angle {\text{BCD + }}\angle {\text{CDB}} = {180^\circ }[{\text{sum of three angles of}} \Delta  is 180^\circ ]...........(2)  $ 

 ${\text{Adding, (1) and (2}})  $

$\angle {\text{BAD + }}\angle {\text{ABD}} + \angle {\text{BDA}} + \angle {\text{CBD}} + \angle {\text{BCD}} + \angle {\text{BCD}} + \angle {\text{CDB}} = {360^\circ }  $

${\text{or }}\angle BAD + (\angle ABD + \angle CBD) + \angle BCD + (\angle CDB + \angle BDA) = {360^\circ }  $

or $\angle BAD + \angle ABC + \angle BCD + \angle CDA = {360^\circ }  $

$\angle A + \angle B + \angle C + \angle D = {360^\circ }  $ 

So, Sum of quadrilateral is 3600

Hence,  proved.

4. ABC is an isosceles triangle with AB=AC. AE bisects the exterior A. Prove that $AE\parallel BC$.

Ans: Since AD bisects the exterior A

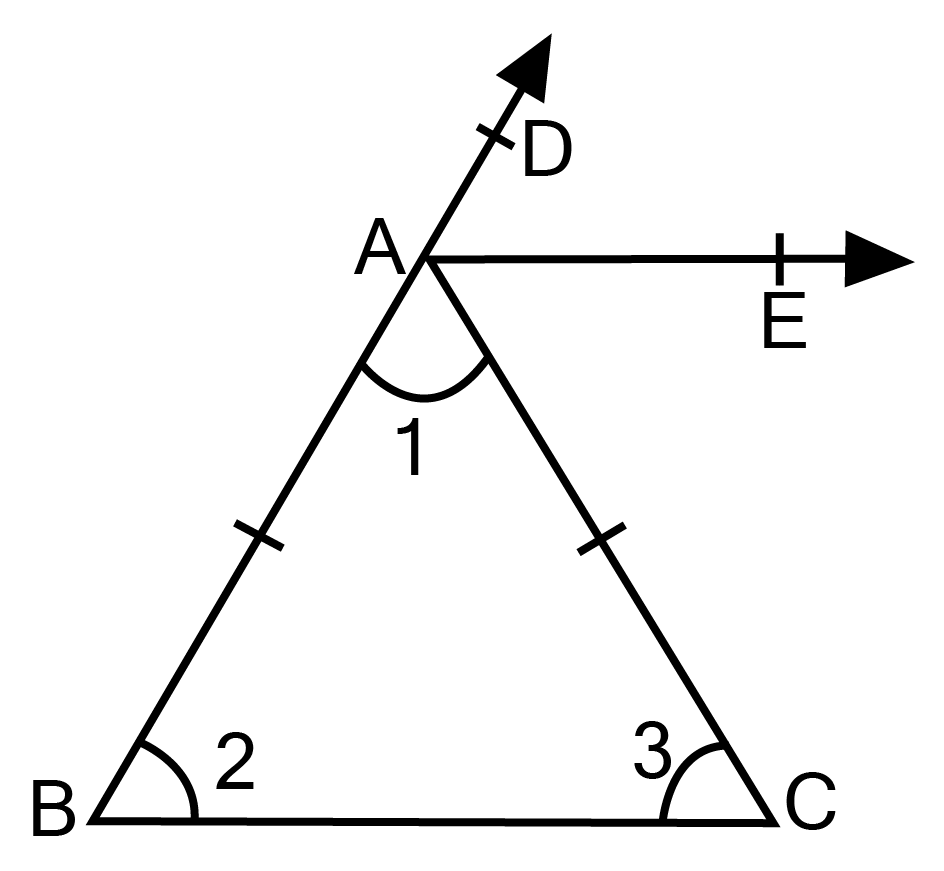
${{\text{ }}\angle {\text{EAD  = }}\dfrac{1}{2}\angle DAC} $ 

${ = \dfrac{1}{2}\left[ {{{180}^\circ } - \angle 1} \right] = {{90}^\circ } - \dfrac{1}{2}\angle 1 \ldots .(i)} $ 

${\left[ {\therefore \angle 1 + \angle DAC = {{180}^\circ }({\text{ Linear pair }})} \right]}$ 

$\angle 1 + \angle 2 + \angle 3 = {{180}^\circ }  $

$\angle 1 + \angle 2 + \angle 2 = {{180}^\circ }$  ${\text{ [ angles opp. To equal sides are also equal , AB=AC]}}$

$2 \angle 2 = {{180}^\circ } - \angle 1  $

But  $ \angle 2=  {{90}^\circ } - \dfrac{1}{2}\angle 1 $ ……………..(ii)

Hence from (i) & (ii)

$ \angle DAE = \angle 2 = \angle ABC$

But these are corresponding angles.

$\therefore AE\parallel BC $

5. ABC is an isosceles triangle in which AB=AC and side BA is produced to D such that AD=AB. Show that BCD is a right angle.

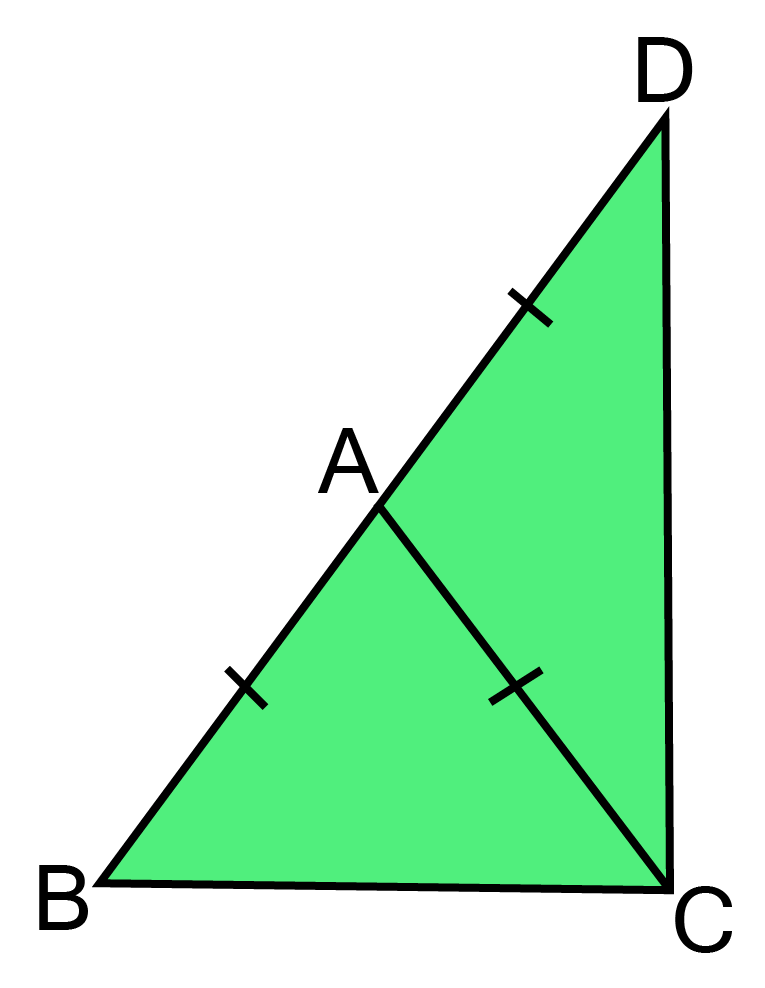
 Ans : $\angle ABC = \angle ACB[{\text{angles opposite to equal side]}}  $

 Also, $\angle {\text{ACD}} = \angle {\text{ADC}}[{\text{angles opposite to equal side}}]$

  Now  

$\angle BAC + \angle CAD = {180^\circ }[{\text{linear pair}}]  $

${\text{Also,}}\angle CAD = \angle ABC + \angle ACB[{\text{exterior angle of}}\vartriangle ABC]  $

$= 2\angle  $

${\text{Also,}}\angle BAC = \angle ACD + \angle ADE   {\text{ACB [exterior angle of }}\vartriangle {\text{ABC]}} $ 

${ = 2\angle {\text{ACD}}} $ 

${\therefore \angle {\text{BAC}} + \angle {\text{CAD}}} $ 

${ = 2(\angle {\text{ACD}} + \angle A{\text{CB}})} $ 

${ = 2\angle {\text{BCD}}} $ 

${{\text{ i}}{\text{.e}}{\text{. }}2\angle {\text{BCD}} = {{180}^\circ }} $ 

${{\text{ or }}\angle {\text{BCD}} = {{90}^\circ }} $

6. In the given figure, $\angle $A=  $\angle $C and AB =BC. Prove that $\vartriangle {\text{ABD}} \cong \vartriangle CBE$

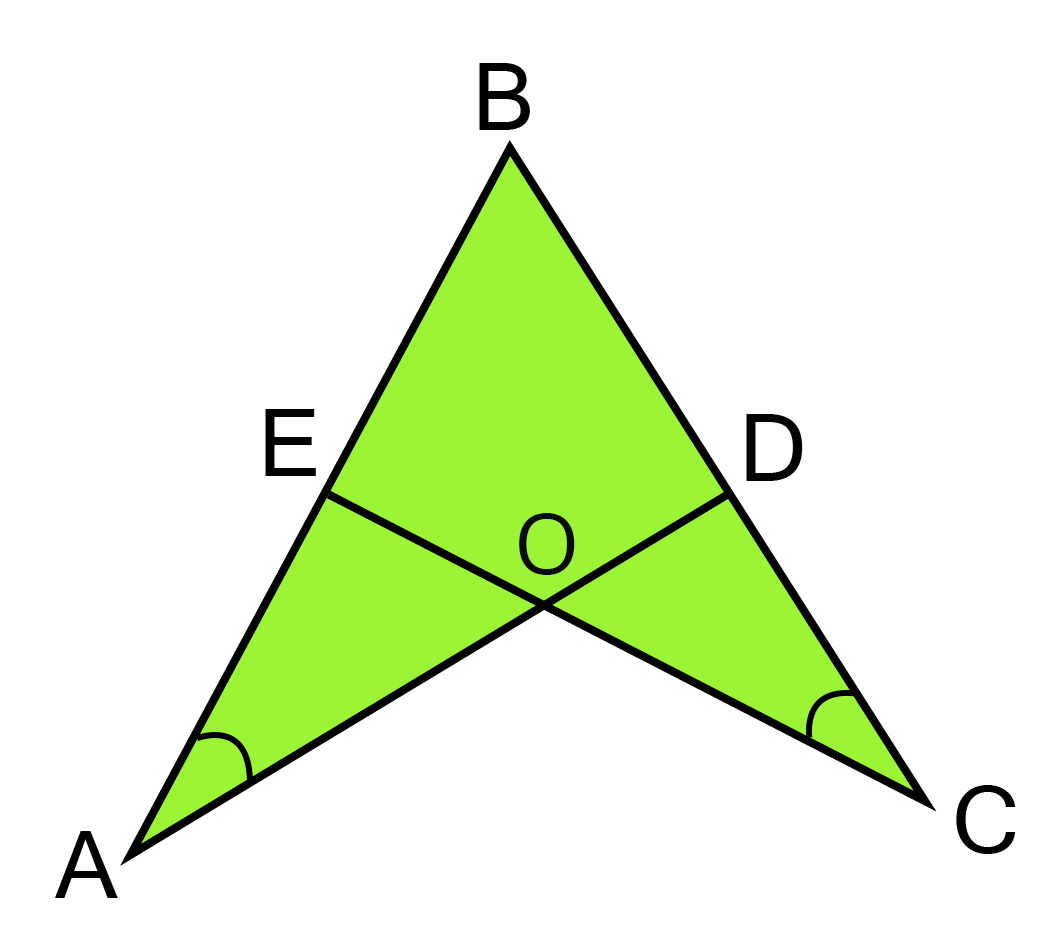
Ans: ${\text{In}} \vartriangle {\text{AOE and }}\vartriangle {\text{COD  }}  $

${\angle {\text{A}} = \angle {\text{C}}[{\text{Given}}]} $ 

${\angle AOE = \angle {\text{COD[vertically opposite angle}}]} $ 

${\therefore \angle {\text{A}} + \angle AOE = \angle C + \angle COD} $ 

$\Rightarrow {180^\circ } - \angle AEO = {180^\circ } - \angle CDO\quad   $

${\angle {\text{A}} + \angle AOE + \angle AEO = {{180}^\circ }{\text{ and }}} $ 

${ \Rightarrow \angle AEO = \angle CDO \to {\text{ (i) }}} $  

Now

$\angle AEO + \angle OEB = {180^\circ }[{\text{linear pair}}]  $

${\text{And}}\angle CDO + \angle ODB = {180^\circ }[{\text{linear pair}}]  $ 

${ \Rightarrow \angle AEO + \angle OEB = \angle CDO + \angle ODB} $ 

${ \Rightarrow \angle OEB = \angle ODB({\text{Using}}({\text{i}})]} $ 

${ \Rightarrow \angle CEB = \angle ADB \to (ii)} $

${\text{Now,in}}\vartriangle ABD\, {\text{and}} \vartriangle CBE,  $

${\angle {\text{A}} = \angle {\text{C}}[{\text{Given}}]} $ 

${\angle {\text{ADB}} = \angle {\text{CEB}}[{\text{From}}({\text{ii}})]} $ 

${{\text{AB}} = {\text{CB}}} $ 

${\vartriangle {\text{ABD}} \cong \vartriangle CBE[{\text{By AAS]}}} $

7. In the given figure, PR>PQ and PS is the bisector of  $ \angle {\text{QPR}}$ Prove that $\angle PSR > \angle PSQ$

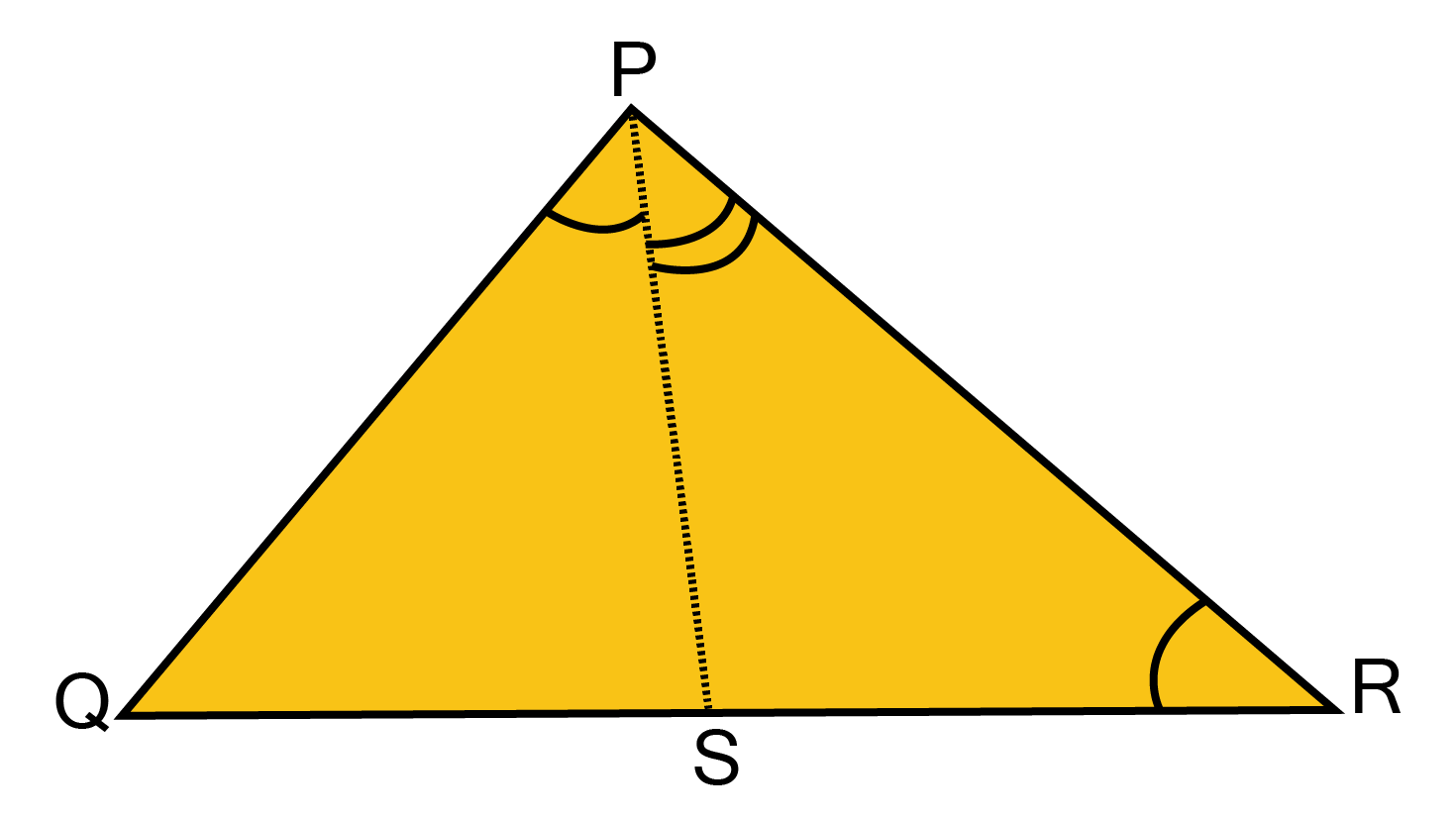
Ans: In $ \Delta {\text{POR}}  $

${\text{ PR}} > {\text{PQ}}  $

$\Rightarrow \angle Q > \angle R {\text{[angle opposite to larger side]}}....(i)  $ 

${\text{Also}},\angle PSR = \angle SPQ + \angle Q {\text{[Exterior angle theorem]}}....(ii)  $

  ${\text{Similarly,}}\angle PSQ = \angle SPR + \angle R  $

  ${\text{But}},\angle SPQ = \angle SPR [{\text{PS bisects}}\angle {\text{QPR}}]  $

  $\therefore \angle PSQ = \angle SPQ + \angle R \ldots .({\text{iii}})  $

  Subtracting (ii) from (iii) 

 $ {\angle PSR - \angle PSQ = (\angle SPQ + \angle Q) - (\angle SPQ + \angle R)} $ 

 ${{\text{ Or }}\angle PSR - \angle PSQ = \angle Q - \angle R \ldots .({\text{iv}})} $ 

 Now

 $ {\angle Q > \angle R} $ 

 ${ \Rightarrow \angle Q - \angle R > 0\quad  \to (v)}$ 

 $ {\text{From (iv) and (iii)}}  $

 ${\angle PSR - \angle PSQ > 0} $ 

 ${\angle PSR > \angle PSQ} $ 

 ${{\text{ Or }}\angle {\text{PSR}} > \angle {\text{PSQ}}}$

Class 9 Maths Triangles Important Questions

The important questions for Class 9 Maths Triangles are based on the problems related to geometrical shapes such as triangles. These problems form the roots of trigonometric problems that will be there in further chapters and higher classes. Students need to be aware of all the important questions of Chapter Triangles Class 9 to score well in the exams. The ultimate goal of a student is to score good in exams and for that, they have to diligently learn all the Triangles Class 9 important questions. 

Class 9 Maths Chapter 7 Important Questions for Triangles

Types of Triangle

On the Basis of the Length of the Sides, There Are Mainly Three Types of Triangles

Scalene Triangle: Length of all the sides of this triangle are different. 

Isosceles Triangle: Length of two sides of a triangle is equal. 

Equilateral Triangle: Length of all the three sides of a triangle are equal.

On the Basis of Angles, There Are Mainly Three Types of Triangles

Acute Angle: All the three angles in an acute angle are less than 90°. 

Obtuse Angle: One angle of the three angles is greater than 90°.

Right Angle: One angle of all the triangles is equal to 90°.

Defining Congruence: If the size and shape of the two figures are the same, then these are known as congruent figures. 

1. Two circles are considered congruent and their radii are of the same size. 

2. Two squares are considered congruent if their sides are of equal size. 

Defining Congruence of Triangles

A triangle is considered to be congruent if all of its corresponding sides and angles are of an equal amount. 

The symbol of congruence is ≅.

Criteria for Congruent Triangles

• Angle-Side-Angle(ASA) Congruence Rule: If two angles and the including side of a triangle is equal to another triangle, they are known as congruent triangles. 

• Side-Angle-Side (SAS) Congruence Rule: If two sides and the including side of a triangle is equal to another triangle, they are known as congruent triangles.

• Side-Side-Side (SSS) Congruence Rule: If all three sides of a triangle are equal to the three corresponding sides of one of another triangle, these are known as congruent triangles.

• Angle-Angle-Side (AAS) Congruence Rule: In two triangles, if any two pairs of angles along with a pair of the corresponding sides is equal, these are known as congruent triangles. 

• Right Angle-Hypotenuse Side  (RHS) Congruence Rule: If the hypotenuse and anyone side are equal of any two right-angled triangles, then they will be known as congruent triangles. 

Some Important Properties of a Triangle

1. The two angles of an isosceles triangle which are opposite to two equal sides are also considered to be equal.

2. Two sides of an isosceles triangle which are opposite to the equal angles are also considered to be equal. This is the converse of the previously mentioned theorem. 

Inequalities in a Triangle

• Theorem 1: The sum of any of the two sides of a triangle will certainly always be greater than the third side.

• Theorem 2: The side which is opposite to the larger angle is always longer, in the given triangle image. This is the converse of the following theorem. 

• Theorem 3: If the two sides seem to be unequal then the angle which is opposite to the longer side is larger, in the previously given triangle image. 

Important Questions of Chapter Triangles Class 9

Question 1. In ΔABC, if ∠B=90°, then write what is the longest side.

Solution:

We know that the side which is opposite to the largest angle in a triangle is the longest side. 

∴The Longest Side=MO

Question 2. If in ΔMNO, ∠M =∠N + ∠O, then write what will be the shape of the given triangle. 

Solution:

Here, ∠M = ∠N + ∠O

In the ΔMNO, by the angle sum property, we have

∠M + ∠N + ∠O=180°

=> ∠M + ∠M =180°

=> 2∠M=180°

∠M=90°

Therefore, the given triangle is clearly right-angled. 

Question 3: Find the length of each of the exterior angles of an equilateral triangle.  

Solution: We know for a fact that each exterior angle of an equilateral triangle is 60°.

∴ Each exterior angle of a triangle=180°-60°=120°

Question 4: Is ΔMNO possible, if MN=6 cm, NO=4 cm and MO=1.5 cm?

Solution:

Since 4+1.5=5.5≠6

Hence, ΔMNO Is not possible. 

Question 5: In ΔPQR, if PQ=PR and ∠Q=70°, find ∠P.

Solution:

In ΔPQR, PQ=PR∠R=∠Q

The∠soppositetoequalsidesofaΔ

The∠soppositetoequalsidesofaΔ

Here, ∠P+∠Q+∠R=180°

=> ∠P+70°+70°=180°

Since∠Q=70°

Since∠Q=70°

=> ∠P=180-70°-70°=40°

Class 9 Maths Chapter 7 Triangles Important Formulas

• Pythagoras Theorem: $\text{In a right triangle, } (Hypotenuse)^2 = (Base)^2 + (Height)^2$

• Area of a Triangle (Heron’s Formula): $\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$, where $s = \frac{a+b+c}{2}$​ is the semi-perimeter and a,b,c are the sides of the triangle.

• Congruence of Triangles Criteria:

• SSS (Side-Side-Side) Criterion

• SAS (Side-Angle-Side) Criterion

• ASA (Angle-Side-Angle) Criterion

• RHS (Right angle-Hypotenuse-Side) Criterion

• Midpoint Theorem: The line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half its length.

• Basic Proportionality Theorem (Thales Theorem): If a line is drawn parallel to one side of a triangle, it divides the other two sides in the same ratio.

Benefits of Class 9 Maths Chapter 7 Triangles Important Questions

• Thorough Concept Clarity: Practising important questions helps students gain a deeper understanding of key concepts like Pythagoras Theorem, congruence of triangles, and properties of triangles.

• Exam-Focused Preparation: These questions are curated based on the CBSE exam pattern, ensuring students are well-prepared to tackle similar problems in their exams.

• Efficient Revision: Important questions serve as a quick and focused revision tool, allowing students to revisit essential topics and identify weak areas before exams.

• Step-by-Step Solutions: Detailed solutions provided with these questions enhance problem-solving skills and help students understand the logical steps required to solve geometry problems.

• Confidence Boost: Regular practice of important questions builds confidence, enabling students to approach exams with a positive mindset and reduced anxiety.

Conclusion

The compilation of important questions for CBSE Class 9 Maths Chapter 7 - "Triangles" is an invaluable resource for students. These questions are strategically curated to encompass critical concepts, theorems, and properties related to triangles, providing a focused approach to exam preparation. They serve as a means for students to assess their understanding, practice problem-solving, and reinforce their knowledge in this fundamental branch of geometry. By closely aligning with the examination pattern and difficulty level, these important questions empower students to build confidence, proficiency, and a deeper appreciation for the elegance and precision of geometric proofs. Overall, they are an indispensable tool for Class 9 Mathematics students, enhancing their academic excellence and problem-solving skills.

Related Study Materials for Class 9 Maths Chapter 7 Triangles

CBSE Class 9 Maths Chapter-wise Important Questions

Related Important Links for Maths Class 9

Along with this, students can also download additional study materials provided by Vedantu for Maths Class 9–