Courses

Courses for Kids

Free study material

Store

Talk to our experts

1800-120-456-456

CBSE

Class 9 Important Question

Maths

Chapter 8: Quadrilaterals

CBSE Class 9 Maths Important Questions - Chapter 8 Quadrilaterals

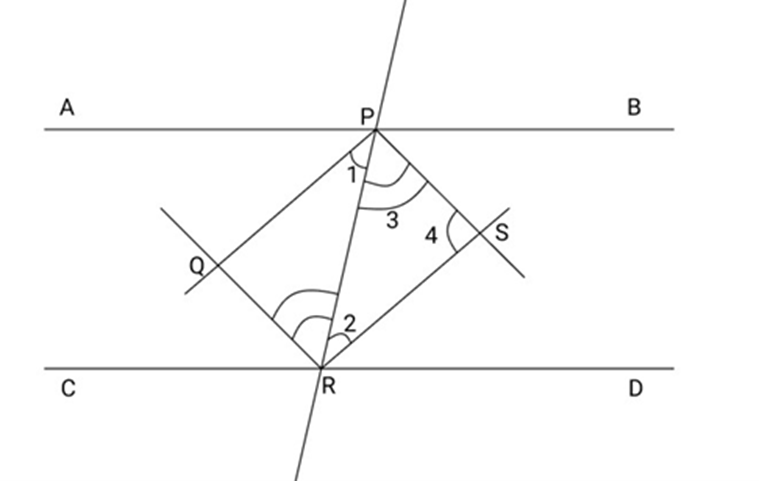
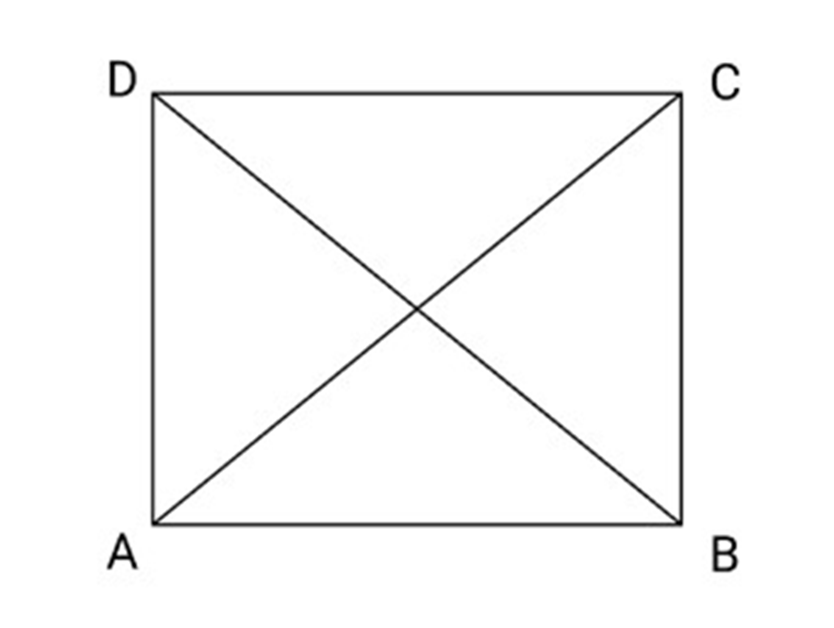
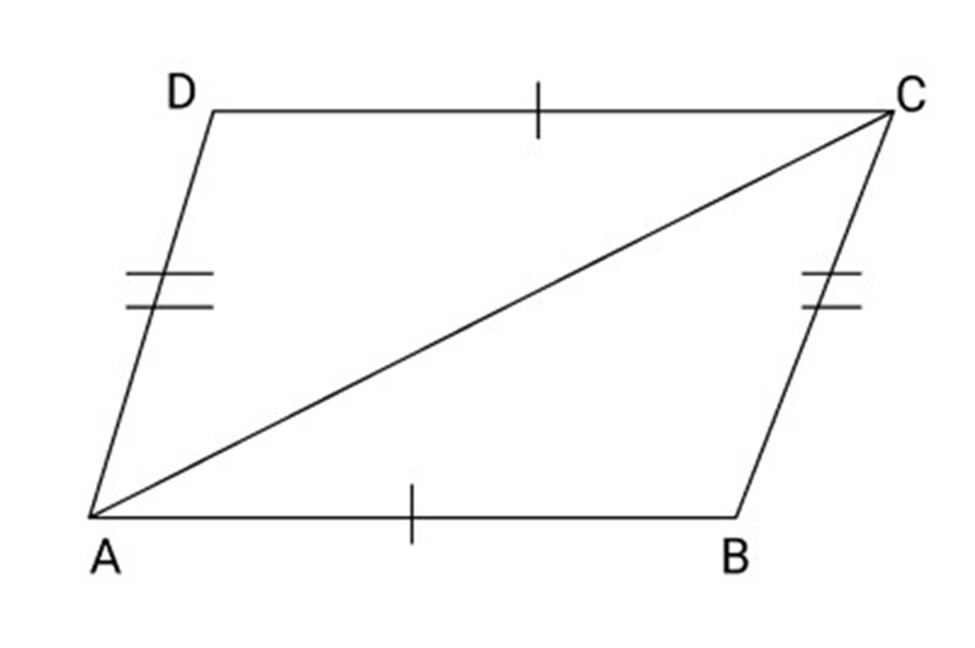
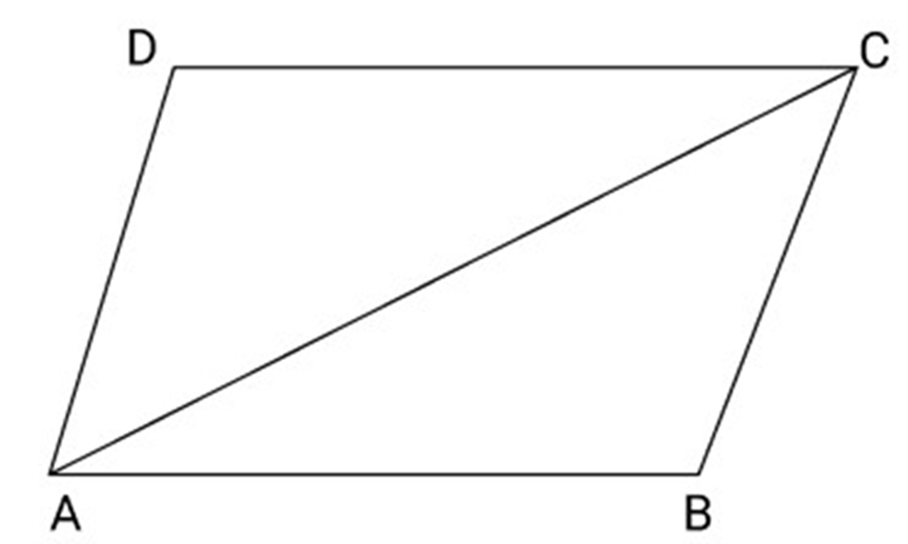
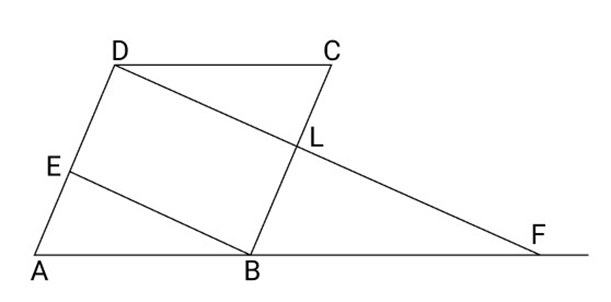
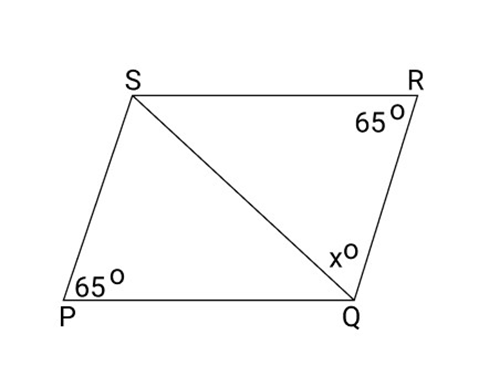
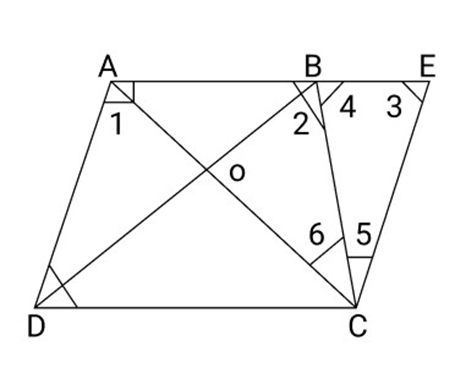
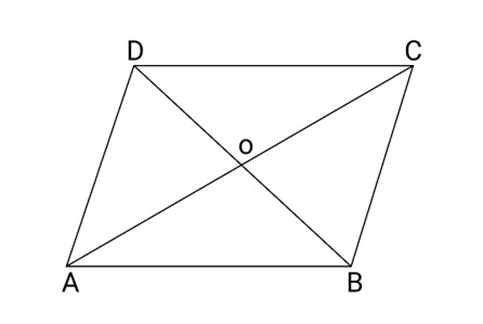
Important Questions for CBSE Class 9 Maths Chapter 8 Quadrilaterals: FREE PDF Download

CBSE Class 9 Maths Chapter 8 Quadrilaterals, explores the properties and types of four-sided polygons, laying the foundation for advanced geometry. Understanding quadrilaterals is crucial as it connects to real-life applications and higher mathematical concepts. This chapter covers theorems like the angle sum property of a quadrilateral, properties of parallelograms, and criteria for proving parallelograms.

The important questions provided for Chapter 8 are carefully curated to align with the CBSE Class 9 Maths syllabus. These questions, along with detailed solutions, offer a structured way to practice and reinforce the concepts. Students can use these questions to improve their problem-solving skills and excel in exams. For added convenience, these Important Questions for Class 9 Maths are available for free download in PDF format, ensuring students have access to reliable study material.

Courses

Access Important Questions for Class 9 Mathematics Chapter 8 - Quadrilaterals

1 Mark Questions

1. A quadrilateral $ABCD$ is a parallelogram if

(a) $AB = CD$

(b) $A B ‖ B C$

(d) $A B = A D$

Ans: (c) $∠ A = 60^{\circ}, ∠ C = 60^{\circ}, ∠ B = 120^{\circ}$

2. In figure, ABCD and AEFG are both parallelogram if $∠ C = 80^{\circ}$ , then $∠ D G F$ is

(a) $100^{\circ}$

(b) $60^{\circ}$

(d) $120^{\circ}$

Ans: (c) $80^{\circ}$

3. In a square ABCD, the diagonals AC and BD bisects at O . Then $△ A O B$ is

(a) Acute angled

(b) Obtuse angled

(d) Right-angled

Ans: (d) Right-angled

4. $ABCD$ is a rhombus. If $∠ A C B = 30^{\circ}$ , then $∠ A D B$ is

(a) $30^{\circ}$

(b) $120^{\circ}$

(d) $45^{\circ}$

Ans: (c) $60^{\circ}$

5. In fig $ABCD$ is a parallelogram. If $∠ D A B = 60^{\circ}$ and $∠ D B C = 80^{\circ}$ then $∠ C D B$ is

(A) $80^{\circ}$

(B) $60^{\circ}$

(D) $40^{\circ}$

Ans: (D) $40^{\circ}$

6. If the diagonals of a quadrilateral bisect each other, then the quadrilateral must be.

(a) Square

(b) Parallelogram

(d) Rectangle

Ans: (b) Parallelogram

7. The diagonal AC and BD of quadrilateral ABCD are equal and are perpendicular bisector of each other then quadrilateral ABCD is a

(a) Kite

(b) Square

(d) Rectangle

Ans: (b) Square

8. The quadrilateral formed by joining the mid points of the sides of a quadrilateral ABCD taken in order, is a rectangle if

(a) $ABCD$ is a parallelogram

(b) $ABCD$ is a rut angle

(d) $AC = BD$

Ans: (a) $ABCD$ is a parallelogram

9. In the fig $ABCD$ is a Parallelogram. The values of $x$ and $y$ are

(a) 30,35

(b) 45,30

(d) 55,35

Ans: (b) 45,30

10. In fig if $DE = 8 cm$ and $D$ is the mid-Point of $AB$ , then the true statement is

(a) $AB = AC$

(b) $DE||BC$

(d) $DE \neq BC$

Ans: (c) $E$ is not mid-Point of AC

11. The sides of a quadrilateral extended in order to form an exterior angler. The sum of these exterior angles is

(a) $180^{\circ}$

(b) $270^{\circ}$

(d) $360^{\circ}$

Ans: (d) $360^{\circ}$

12. $ABCD$ is rhombus with $∠ A B C = 40^{\circ}$ . The measure of $∠ A C D$ is

(a) $90^{\circ}$

(b) $20^{\circ}$

(d) $70^{\circ}$

Ans: (b) $20^{\circ}$

13. In fig $D$ is mid-point of $AB$ and BC then AE is equal to

(a) AD

(b) $EC$

(d) $BC$

Ans: (b) EC

14. In fig $D$ and $E$ are mid-points of $AB$ and AC respectively. The length of DE is

(a) $8.2 cm$

(b) $5.1 cm$

(d) $4.1 cm$

Ans: (d) $4.1 cm$

15. A diagonal of a parallelogram divides it into

(a) Two congruent triangles

(b) Two similes triangles

(d) None of these

Ans: (a) Two congruent triangles

16. A quadrilateral is a, if it’s opposite sides are equal:

(a) Kite

(b) Trapezium

(d) Parallelogram

Ans: (d) Parallelogram

17. In the adjoining Fig. $AB = AC . CD | | BA$ and $AD$ is the bisector of $∠ P A C$ prove that

(a) $∠ D A C = ∠ B C A$

Ans: In $Δ A B C A B = A C$ is given.

$∴ ∠ B = ∠ C$

$[a n g l e o p p o s i t e t o e q u a l s i d e s o f t h e Δ]$

$\Rightarrow ∠ B C A = ∠ A B C$ (Opposite angle of equal sides are equal)

$∠ P A C = ∠ B C A + ∠ A B C$ (Exterior angle)

$2 ∠ C A D = 2 ∠ B C A$

$\Rightarrow ∠ D A C = ∠ B C A$

Hence proved.

(b) ABCD is a parallelogram

Ans: Now, $∠ P A C = ∠ B C A$

Also $C D ∥ B A$ (According to the question)

$∴ A B C D$ is a parallelogram.

18. Which of the following is not a parallelogram?

(a) Rhombus

(b) Square

(d) Rectangle

Ans: (c) Trapezium

19. The sum of all the four angles of a quadrilateral is

(a) $180^{0}$

(b) $360^{0}$

(d) $90^{0}$

Ans: (b) $360^{\circ}$

20. In Fig ABCD is a rectangle P and $Q$ are mid-points of AD and DC respectively. Then length of $PQ$ is

(a) 5 $cm$

(b) $4 cm$

(d) $2 cm$

Ans: (c) $2.5 cm$

21. In Fig ABCD is a rhombus. Diagonals AC and BD intersect at $0. E$ and $F$ are mid points of AO and BO respectively. If $A C = 16 cm$ and $B D = 12 cm$ then EF is

(a) $10 cm$

(b) $5 cm$

(d) $6 cm$

Ans: (b) $5 cm$

2 Marks Questions

1. The angles of a quadrilateral are in the ratio 3: 5: 9: 13. Find all angles of the quadrilateral

Ans: Assume that in quadrilateral $ABCD, ∠ A = 3 x, ∠ B = 5 x, ∠ C = 9 x$ and $∠ D = 13 x$ .

We know that the sum of all the angles of a quadrilateral $= 360^{\circ}$

So, $∠ A + ∠ B + ∠ C + ∠ D = 360^{\circ} \Rightarrow 3 x + 5 x + 9 x + 13 x = 360^{\circ}$

$\Rightarrow 30 x = 360^{\circ} \Rightarrow x = 12^{\circ}$

Now, $∠ A = 3 x = 3 \times 12 = 36^{\circ}$

$∠ B = 5 x = 5 \times 12 = 60^{\circ}$

$∠ C = 9 x = 9 \times 12 = 108^{\circ}$

And $∠ D = 13 x = 13 \times 12 = 156^{\circ}$

Therefore, angles of a given quadrilateral are $36^{\circ}, 60^{\circ}, 108^{\circ}$ and $156^{\circ}$ .

2. If the diagonals of a parallelogram are equal, show that it is a rectangle.

Ans: According to the question: $ABCD$ is a parallelogram with diagonal $AC =$ diagonal BD

To prove: $ABCD$ is a rectangle.

Proof: In triangles $ABC$ and $ABD$ ,

$AB = AB$ (Common)

$AC = BD$ (According to the question)

$AD = BC$ (Opposite Sides of a

So, $Δ ABC ≅ Δ BAD$ (By SSS congruence)

$\Rightarrow ∠ DAB = ∠ CBA (By C . P . C . T .) \dots \dots \dots . . (i)$

But $∠ DAB + ∠ CBA = 180^{\circ} \dots \dots \dots$ (ii)

and $AB$ cuts them, the sum of the interior angles of the same side of transversal is $180^{\circ}$ )

According to the equations (i) and (ii),

$∠ DAB = ∠ CBA = 90^{\circ}$

Therefore, $ABCD$ is a rectangle.

3. Diagonal AC of a parallelogram ABCD bisects $∠$ A (See figure). Show that:

(i) It bisects $∠ C$ also.

(ii) $ABCD$ is a rhombus.

Diagonal AC of a parallelogram ABCD bisects

Ans: Diagonal AC bisects $∠ A$ of the parallelogram $ABCD$ .

(i) Since and AC intersects them.

So, $∠ 1 = ∠ 3$ (Alternate angles) ..........(i)

Similarly $∠ 2 = ∠ 4 \dots \dots \dots . .$ (ii)

But $∠ 1 = ∠ 2$ (Given) ..........(iii)

So, $∠ 3 = ∠ 4$ (Using eq. (i), (ii) and (iii))

Hence $AC$ bisects $∠ C$ .

(ii) $∠ 2 = ∠ 3 = ∠ 4 = ∠ 1$

$\Rightarrow AD = CD$ (Sides opposite to equal angles)

So, $AB = CD = AD = BC$

Therefore ABCD is a rhombus.

4. ABCD is a parallelogram and AP and Care the perpendiculars from vertices $A$ and $C$ on its diagonal BD (See figure). Show that:

(i) $Δ APB ≅ Δ CQD$

(ii) $AP = CQ$

Ans: According to the question,

ABCD is a parallelogram.

$A P ⊥ B D$ and $C Q ⊥$ BD

To prove:

(i) $Δ APB ≅ Δ CQD$

(ii) $AP = CQ$

Proof:

(i) In $Δ APB$ and $Δ CQD$ ,

$∠ 1 = ∠ 2$ (Alternate interior angles)

$A B = C D$ (Opposite sides of a parallelogram are equal)

$∠ APB = ∠ CQD = 90^{\circ}$

So, $Δ APB ≅ Δ CQD$ (By ASA Congruency)

(ii) Since $Δ APB ≅ Δ CQD$

$AP = CQ$ (By C.P.C.T.)

Hence proved.

5. ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See figure). AC is a diagonal. Show that:

(i) and $SR = \frac{1}{2} AC$

(ii) $PQ = SR$

(iii) PQRS is a parallelogram.

Ans: (i) In $△ DAC, S$ is the mid point of $DA$ and $R$ is the mid point of $DC$ . Therefore, $SR ‖ AC$ and $SR = \frac{1}{2} AC$ .By mid-point theorem.

(ii) In $△ BAC, P$ is the mid point of $AB$ and $Q$ is the mid point of $BC$ . Therefore, $PQ ‖ AC$ and $P Q = \frac{1}{2} AC$ .By mid-point theorem. But from (i) $SR = \frac{1}{2} AC$ therefore $P Q = SR$

(iii) $PQ ‖ AC$ \& SR $‖ AC$ therefore $PQ ‖ SR$ and $P Q = SR$ . Hence, a quadrilateral with opposite sides equal and parallel is a parallelogram. Therefore PQRS is a parallelogram.

6. The angles of a quadrilateral are in the ratio 3:5:9:13. Find all the angles of the quadrilateral.

Ans: Assume that angles of quadrilateral $ABCD$ are $3 x, 5 x, 9 x$ , and $13 x$

$∠ A + ∠ B + ∠ C + ∠ D = 360^{\circ}$ (We know that the sum of angles of a quadrilateral is $360^{\circ})$

$30 x = 360^{\circ}$

$x = 12^{\circ}$

So, $∠ A = 3 x = 3 \times 12 = 36^{\circ}$

$∠ B = 5 x = 5 \times 12 = 60^{\circ}$

$∠ C = 9 x = 9 \times 12 = 108^{\circ}$

$∠ D = 13 x = 13 \times 12 = 156^{\circ}$

Hence, the value of all angles are $36^{\circ}, 60^{\circ}, 108^{\circ}, 156^{\circ} .$

7. Show that each angle of a rectangle is a right angle.

Ans: As we also know that a rectangle is a parallelogram whose one angle is right angle.

Assume that $ABCD$ be a rectangle.

$∠ A = 90^{\circ}$

To prove $∠ B = ∠ C = ∠ D = 90^{\circ}$

Proof:

and $AB$ is transversal

So, $∠ A + ∠ B = 180^{\circ}$

$90^{\circ} + ∠ B = 180^{\circ}$

$∠ B = 180^{\circ} - 90^{\circ} = 90^{\circ}$

$∠ C = ∠ A$

So, $∠ C = 90^{\circ}$

$∠ D = ∠ B$

So, $∠ D = 90^{\circ}$

Hence proved.

8. A transversal cuts two parallel lines prove that the bisectors of the interior angles

enclose a rectangle.

Ans: According to the question,

and EF cuts them at $P$ and $R$ .

$∠ A P R = ∠ P R D$ (Alternate interior angles)

So, $\frac{1}{2} ∠ A P R = \frac{1}{2} ∠ P R D$

i.e. $∠ 1 = ∠ 2$

(Alternate)

Hence, proved.

9. Prove that diagonals of a rectangle are equal in length.

Ans: $ABCD$ is a rectangle and AC and BD are diagonals.

To prove $A C = B D$

Proof:

In $Δ D A B$ and CBA

$AD = BC$ (In a rectangle opposite sides are equal)

$∠ A = ∠ B (90^{\circ} each)$

$AB = AB$ (common)

So, $Δ D A B ≅ Δ C A B$ (By SAS)

So, $A C = B D$ (By C.P.C.T)

10. If each pair of opposite sides of a quadrilateral is equal, then prove that it is a parallelogram.

Ans: According to the question,

A quadrilateral $ABCD$ in which $AB = DC$ and $AD = BC$

Pair of opposite sides of a quadrilateral is equal

To prove:

$ABCD$ is a parallelogram

We construct a line AC to with join point A with point C.

Proof: In $△ A B C$ and $△ A D C$

$AD = BC$ (According to the question)

$AB = DC$

$AC = AC$ (common)

So, $Δ A B C ≅ Δ A D C$ (By SSS )

So, $∠ B A C = ∠ D A C$ (By CPCT)

So, $A B C D$ is a parallelogram.

12. Show that the line segments joining the mid points of opposite sides of a quadrilateral bisect each other.

Ans: According to the question,

$ABCD$ is quadrilateral $E, F, G, H$ are mid points of the side $AB, BC, CD$ and $DA$ respectively

To prove:

EG and HF bisect each other.

In $△ A B C, E$ is mid-point of $AB$ and $F$ is mid-point of $BC$

So, and $E F = \frac{1}{2} A C \dots \dots . (i)$

Similarly, and $H G = \frac{1}{2} A C \dots \dots . (i i)$

According to equations (i) and (ii),

and $E F = G H$

So, $E F G H$ is a parallelogram and EG and HF are its diagonals

The diagonals of a parallelogram bisect each other

Hence, EG and HF bisect each other.

Line segments joining the mid points of opposite sides of a quadrilateral bisect

13. ABCD is a rhombus show that diagonal AC bisects $∠ A$ as well as $∠ C$ and diagonal BD bisects $∠ B$ as well as $∠ D$

Ans: According to the question,

$ABCD$ is a rhombus

In $Δ A B C$ and $Δ A D C$

$A B = A D$ (Sides of a rhombus)

$B C = D C$ (Sides of a rhombus)

$A C = A C$ (Common)

So, $Δ A B C ≅ Δ A D C$ (By SSS Congruency)

So, $∠ C A B = ∠ C A D$ and $∠ A C B = ∠ A C D$

Therefore, AC bisects $∠ A$ as well as $∠ C$

Similarly, by joining B to D, we can prove that $△ A B D ≅ Δ C B D$

Therefore, BD bisects $∠ B$ as well as $∠ D$

14. In fig AD is a median of $△ A B C, E$ is mid-Point of AD. BE produced meet AC at $F$ . Show that $A F = \frac{1}{3} A C$

Ans: Suppose $M$ is mid-Point of CF Join DM

So,

In $△ A D M, E$ is mid- Point of AD and

is mid-point of AM

So, $A F = F M$

$FM = MC$

So, $A F = F M = M C$

So, $A C = A F + F M + M C$

$= A F + A F + A F$

$\Rightarrow A C = 3 A F$

$\Rightarrow A F = \frac{1}{3} A C$

Hence Proved.

15. Prove that a quadrilateral is a parallelogram if the diagonals bisect each other.

Ans: According to the given figure,

$ABCD$ is a quadrilateral in which diagonals AC and BD intersect each other at O

In $△ A O B$ and $△ D O C$

$O A = O C$ (Given)

$O B = O D$ (Given)

And $∠ A O B = ∠ C O D$ (Vertically apposite angle)

So, $△ A O B ≅ Δ C O D$ (By SAS)

So, $∠ O A B = ∠ O C D$ (By C.P.C.T)

But this is Pair of alternate interior angles

So, $A D ∥ B C$

So, Quadrilateral $ABCD$ is a Parallelogram.

16. In fig ABCD is a Parallelogram. AP and Care Perpendiculars from the Vertices $A$ and C on diagonal BD.

$Parallelogram abcd with . AP and Care Perpendiculars from the Vertices ${\text{A}}$ and C on diagonal BD.$

Show that

(i) $△ A P B ≅ Δ C Q D$

(ii) $A P = C Q$

Ans: (I) in $Δ A P B$ and $Δ C Q D$

$AB = DC$ (Opposite sides of a Parallelogram)

$∠ P = ∠ Q$ (each $90^{\circ}$ )

And $∠ A B P = ∠ C D Q$

So, $△ A P B ≅ Δ C Q D$ (By ASA)

(II) So, $A P = C Q$ (By C.P.C.T)

17. ABCD is a Parallelogram $E$ and $F$ are the mid-Points of $BC$ and AD respectively. Show that the segments BF and DE trisect the diagonal AC.

$Parallelogram ABCD ${\text{E}}$ and ${\text{F}}$ are the mid-Points of ${\text{BC}}$ and AD respectively.$

Ans: $F D ∥ B E$ and $F D = B E$

So, BEDF Is a Parallelogram

$EG ∥ BH$ and $E$ is the mid-Point of BC

So, $G$ is the mid-point of $HC$

Or $HG = GC \dots \dots \dots \dots . .$ (i)

Similarly $AH = HG \dots \dots \dots \dots . .$ (ii)

According to equations (i) and (ii) we get

$AH = HG = GC$

Hence, the segments BF and DE bisects the diagonal AC.

18. Prove that if each pair of apposite angles of a quadrilateral is equal, then it is a parallelogram.

Ans: According to the figure and question,

$ABCD$ is a quadrilateral in which $∠ A = ∠ C$ and $∠ B = ∠ D$

To Prove:

$ABCD$ is a parallelogram

Proof:

$∠ A = ∠ C$ (According to the question)

$∠ B = ∠ D$ (According to the question)

$∠ A + ∠ B = ∠ C + ∠ D \dots \dots (i)$

In quadrilateral. ABCD

$∠ A + ∠ B + ∠ C + ∠ D = 360^{\circ}$

$(∠ A + ∠ B) + (∠ A + ∠ B) = 360^{\circ} (By \dots . (i))$

$∠ A + ∠ B = 180^{\circ}$

$∠ A + ∠ B = ∠ C + ∠ D = 180^{\circ}$

These are sum of interior angles on the same side of transversal

So, $A D ‖ B C$ and $A B ‖ D C$

So, ABCD is a parallelogram.

19. In Fig. ABCD is a trapezium in which $AB | | DCE$ is the mid-point of AD. A line through $E$ is parallel to AB show that $l$ bisects the side BC

$ABCD is a trapezium in which ${\text{AB}}||{\text{DCE}}$$

Ans: We draw a line AC with join point A to Point C.

In $Δ A D C$

E is mid-point of $AD$ and $EO | | DC$

So, $O$ is mid point of $AC$ (A line segment joining the midpoint of one side of a triangle parallel to second side and bisect the third side)

In $△ A C B$

$O$ is mid point of $AC$

OF || $A B$

So, F is mid point of BC

So, EF Bisect BC.

20. In Fig. ABCD is a parallelogram in which $X$ and $Y$ are the mid-points of the sides DC and AB respectively. Prove that AXCY is a parallelogram

$ABCD is a parallelogram in which ${\text{X}}$ and ${\text{Y}}$ are the mid-points of the sides DC and AB respectively.$

Ans: According to the given figure,

$ABCD$ is a parallelogram

So, and $AB = CD$

And $\frac{1}{2} A B = \frac{1}{2} C D$

And $X C = A Y$

(X and Y are mid-point of DC and AB respectively)

$\Rightarrow A X C Y$ is a parallelogram

$${\text{ABCD}}$ is a parallelogram$

21. The angles of quadrilateral are in the ratio 3:5:10:12. Find all the angles of the quadrilateral.

Ans: Assume that angles of quadrilaterals are

3x, 5x, 10x, and 12x

$∠ A = 3 x, ∠ B = 5 x, ∠ C = 10 x, ∠ D = 12 x$

In a quadrilateral

$∠ A + ∠ B + ∠ C + ∠ D = 360^{\circ}$

$3 x + 5 x + 10 x + 12 x = 360^{\circ}$

$30 x = 360$

$x = \frac{360}{30} = 12$

$∠ A = 3 \times 12 = 36^{\circ}, ∠ B = 5 \times 12 = 60^{\circ}$

$∠ C = 10 \times 12 = 120^{\circ}, ∠ D = 12 \times 12 = 144^{\circ}$

Hence, the values of all angles are $36^{\circ}, 60^{\circ}, 120^{\circ}, 144^{\circ} .$

22. In fig $D$ is mid-points of AB. $P$ is on AC such that $P C = \frac{1}{2} A P$ and $D E ∥ B P$ show that $A E = \frac{1}{3} A C$

$fig ${\text{D}}$ is mid-points of AB. $P$ is on AC$

Ans: According to $Δ$ ABP

$D$ is mid points of $AB$ and $DE ∣ BP$

$E$ is midpoint of $AP$

So, $A E = E P$ also $P C = \frac{1}{2} A P$

$2 PC = AP$

$2 PC = 2 AE$

$\Rightarrow PC = AE$

So, $A E = P E = P C$

So, $A C = A E + E P + P C$

$AC = AE + AE + AE$

$\Rightarrow AE = \frac{1}{3} AC$

Hence Proved.

23. Prove that the bisectors of the angles of a Parallelogram enclose a rectangle. It is given that adjacent sides of the parallelogram are unequal.

Ans: According to the given figure,

$A B C D$ is a parallelogram

So, $∠ A + ∠ D = 180^{\circ}$

or $\frac{1}{2} (∠ A + ∠ D) = 90^{\circ}$

Or $∠ A P D = 90^{\circ}$ (We know that the sum of all angles of a triangle is $180^{\circ}$ )

So, $∠ S P Q = ∠ A P D = 90^{\circ}$

Similarly, $∠ Q R S = 90^{\circ}$ and $∠ P Q R = 90^{\circ}$

$∠ P + ∠ Q + ∠ R + ∠ S = 360^{\circ}$

So, $∠ P S R = 90^{\circ}$ .

Hence, each angle of quadrilateral PQRS is $90^{\circ}$ .

Therefore, PQRS is a rectangle.

24. Prove that a quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.

Ans: According to the question and figure,

$ABCD$ is a quadrilateral in which $AB | | DC$ and $BC | | AD$ .

To Prove:

$ABCD$ is a parallelogram

quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.

Construction: Join AC and BD intersect each other at $O$ .

Proof:

$△ A O B ≅ Δ D O C$ (By AAA)

Because $∠ 1 = ∠ 2$

$∠ 3 = ∠ 4$ and $∠ 5 = ∠ 6$

So, $AO = OC$

And $BO = OD$

So, $ABCD$ is a parallelogram

Because, diagonals of a parallelogram bisect each other.

3 Marks Questions

1. Show that is diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Ans: According to the question and figure,

Suppose $ABCD$ is a quadrilateral.

Suppose its diagonal AC and BD bisect each other at right angle at point $O$ .

diagonals of a quadrilateral bisect each other at right angles

So, $O A = O C, O B = O D$

And $∠ AOB = ∠ BOC = ∠ COD = ∠ AOD = 90^{\circ}$

To prove:

$ABCD$ is a rhombus.

Proof:

In $Δ AOD$ and $Δ BOC$ ,

$OA = OC$ (According to the figure)

$∠ AOD = ∠ BOC$ (According to the figure)

$OB = OD$ ?(According to the figure)

So, $Δ AOD ≅ Δ COB$ (By SAS congruency)

$\Rightarrow AD = CB$ (By C.P.C.)..........(i)

Again, In $Δ AOB$ and $Δ COD$ ,

$OA = OC$ (According to the figure)

$∠ AOB = ∠ COD$ (According to the figure)

$OB = OD$ (According to the figure)

So, $Δ AOB ≅ Δ COD$ (By SAS congruency)

$\Rightarrow AD = CB$ (By C.P.C.T.) ..........(ii)

Now In $Δ AOD$ and $Δ BOC$ ,

$OA = OC$ (According to the figure)

$∠ AOB = ∠ BOC$ (According to the figure)

$OB = OB$ (Common)

So, $Δ AOB ≅ Δ COB$ (By SAS congruency)

$\Rightarrow AB = BC$ (By C.P.C.T)..........(iii)

According to the equations (i), (ii) and (iii),

$AD = BC = CD = AB$

And the diagonals of quadrilateral ABCD bisect each other at right angle.

Hence, $ABCD$ is a rhombus.

2. Show that the diagonals of a square are equal and bisect each other at right angles.

Ans: According to the question and figure,

ABCD is a square.

AC and BD are its diagonals bisect each other at point O.

diagonals of a square are equal and bisect each other at right angles

To prove:

$AC = BD$ and $AC ⊥ BD$ at point $O$ .

Proof:

In triangles $ABC$ and BAD,

$AB = AB$ (Common)

$∠ ABC = ∠ BAD = 90^{\circ}$

$BC = AD$ (Sides of a square)

So, $Δ ABC ≅ Δ BAD$ (By SAS congruency)

$\Rightarrow AC = BD$ (By C.P.C.T.)

Hence proved.

Now in triangles $AOB$ and AOD,

$AO = AO$ (Common)

$AB = AD$ (Sides of a square)

OB = OD (Diagonals of a square bisect each other)

So, $Δ AOB ≅ Δ AOD$ (By SSS congruency)

$∠ AOB = ∠ AOD$ (By C.P.C.T.)

But $∠ AOB + ∠ AOD = 180^{\circ}$ (Linear pair)

So, $∠ AOB = ∠ AOD = 90^{\circ}$

$\Rightarrow O A ⊥ B D$ or $A C ⊥ B D$

Hence proved.

3. ABCD is a rhombus. Show that the diagonal AC bisects $∠ A$ as well as $∠ C$ and diagonal BD bisects $∠ B$ as well as $∠ D$ .

Ans: ABCD is a rhombus.

Hence, $A B = B C = C D = A D$

Suppose $O$ be the point of bisection of diagonals.

So, $OA = OC$ and $OB = OD$

In $Δ AOB$ and $Δ AOD$ ,

$OA = OA$ (Common)

$AB = AD$ (Equal sides of rhombus)

$OB = OD$ (Diagonals of rhombus bisect each other)

So, $Δ AOB ≅ Δ AOD$ (By SSS congruency)

$\Rightarrow ∠ OAD = ∠ OAB$ (By C.P.C.T.)

$\Rightarrow$ OA bisects $∠ A$ ..........(i)

Similarly $Δ BOC ≅ Δ DOC$ (By SSS congruency)

$\Rightarrow ∠ OCB = ∠ OCD$ (By C.P.C.T.)

$\Rightarrow OC$ bisects $∠ C \dots \dots \dots$ .

(ii)

According to the equations (i) and (ii), we can say that diagonal AC bisects $∠ A$ and $∠ C$ .

Now in $Δ AOB$ and $Δ BOC$ ,

$OB = OB$ (Common)

$AB = BC$ (Equal sides of rhombus)

$OA =$ OC (Diagonals of rhombus bisect each other)

So, $Δ AOB ≅ Δ COB$ (By SSS congruency)

$\Rightarrow ∠ OBA = ∠ OBC$ (By C.P.C.T.)

$\Rightarrow OB$ bisects $∠ B \dots \dots \dots$

(iii)

Similarly $Δ AOD ≅ Δ COD$ (By SSS congruency)

$\Rightarrow ∠ ODA = ∠ ODC$ (By C.P.C.T.)

$\Rightarrow$ BD bisects $∠ D \dots \dots \dots$ ..(iv)

According to the equations (iii) and (iv), we can say that diagonal BD bisects $∠ B$ and $∠ D$ .

4. In parallelogram ABCD, two points $P$ and $Q$ are taken on diagonal BD such that DP = B(See figure). Show that:

(i) $Δ APD ≅ Δ CQB$

(ii) $AP = CQ$

(iii) $Δ AQB ≅ △ CPD$

(iv) $AQ = CP$

(v) APCis a parallelogram.

Ans: (i) In $Δ$ APD and $Δ$ CQB,

$DP = BQ$ (According to the figure)

$∠ ADP = ∠ QBC$ (Alternate angles and $BD$ is transversal))

$AD = CB$ (Opposite sides of parallelogram)

So, $Δ APD ≅ Δ CQB$ (By SAS congruency)

(ii) Since $Δ APD ≅ Δ CQB$

$\Rightarrow AP = CQ$ (By C.P.C.T.)

(iii) In $Δ AQB$ and $Δ CPD$ ,

$BQ = DP$ (According to the figure)

$∠ ABQ = ∠ PDC$ (Alternate angles and $BD$ is transversal))

$AB = CD$ (Opposite sides of parallelogram)

$Δ AQB ≅ Δ CPD$ (By SAS congruency )

(iv) Since $Δ AQB ≅ Δ CPD$

$\Rightarrow AQ = CP$ (By C.P.C.T.)

(v) In quadrilateral APCQ,

$AP =$ C(Proved in part (i))

$AQ = CP$ (Provedin part (iv))

Since opposite sides of quadrilateral APCare equal.

Therefore, APCis a parallelogram.

5. ABCD is a rhombus and P, Q, R, S are mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.

Ans: According to the question and figure,

P, Q, R and S are the mid-points of respective sides AB, BC, CD and DA of rhombus. PQ, QR, RS and SP are joined.

To prove:

PQRS is a rectangle.

We draw a line AC with join point A to Point C.

Proof:

In $Δ ABC, P$ is the mid-point of $AB$ and $Q$ is the mid-point of $BC$ .

So, and $P Q = \frac{1}{2} A C \dots \dots \dots .$ (i)

In $Δ ADC, R$ is the mid-point of $CD$ and $S$ is the mid-point of $AD$ .

So, and $SR = \frac{1}{2}$ AC..........(ii)

According to the equations (i) and (ii),

$P Q ∥ S R$ and $P Q = S R$

So, PQRS is a parallelogram.

Now ABCD is a rhombus. (According to the question)

So, $A B = B C$

$\Rightarrow \frac{1}{2} AB = \frac{1}{2} BC \Rightarrow PB = BQ$

So, $∠ 1 = ∠ 2$ (Angles opposite to equal sides are equal)

Now in triangles APS and CQR, we have,

$AP = CQ (P$ and $Q$ are the mid-points of $AB$ and $BC$ and $AB = BC$ )

Similarly AS = CR and PS = QR (Opposite sides of a parallelogram)

$Δ APS ≅ Δ CQR$ (By SSS congreuancy)

$\Rightarrow ∠ 3 = ∠ 4$ (By C.P.C.T.)

Now we have $∠ 1 + ∠ SPQ + ∠ 3 = 180^{\circ}$

And $∠ 2 + ∠ PQR + ∠ 4 = 180^{\circ}$ (Linear pairs)

So, $∠ 1 + ∠ SPQ + ∠ 3 = ∠ 2 + ∠ PQR + ∠ 4$

Since $∠ 1 = ∠ 2$ and $∠ 3 = ∠ 4$ (Proved above)

So, $∠ SPQ = ∠ PQR \dots \dots \dots .$ (iii)

Now PQRS is a parallelogram (Proved above)

So, $∠ SPQ + ∠ PQR = 180^{\circ} \dots \dots \dots$ .(iv) (Interior angles)

Using equations (iii) and (iv),

$∠ SPQ + ∠ SPQ = 180^{\circ} \Rightarrow 2 ∠ SPQ = 180^{\circ}$

$\Rightarrow ∠ SPQ = 90^{\circ}$

Hence, PQRS is a rectangle.

6. $ABCD$ is a rectangle and P, Q, R and S are the mid-points of the sides $AB, BC, CD$ and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Ans: According to the question,

A rectangle $ABCD$ in which $P, Q, R$ and $S$ are the mid-points of the sides $AB, BC$ , CD and DA respectively. PQ, QR, RS and SP are joined.

$${\text{ABCD}}$ is a rectangle and P, Q, R and S are the mid-points of the sides ${\text{AB}},{\text{BC}},{\text{CD}}$ and DA respectively$

To prove:

PQRS is a rhombus.

We draw a line AC with join point A to Point C.

Proof:

In $Δ ABC, P$ and $Q$ are the mid-points of sides $AB, BC$ respectively.

So, and $PQ = \frac{1}{2} AC \dots \dots \dots .$ (i)

In $Δ ADC, R$ and $S$ are the mid-points of sides $CD, AD$ respectively.

So, and $SR = \frac{1}{2} AC \dots \dots \dots$ (ii)

According to the equations (i) and (ii),

$PQ ∥ SR$ and $PQ = SR$ ..........(iii)

So, PQRS is a parallelogram.

Now $ABCD$ is a rectangle. (According to the question)

So, $A D = B C$

$\Rightarrow \frac{1}{2} AD = \frac{1}{2} BC \Rightarrow AS = BQ \dots \dots \dots .$ (iv)

In triangles APS and BPQ,

$AP = BP$ (P is the mid-point of $AB$ )

$∠ PAS = ∠ PBQ (Each 90^{\circ})$

And $A S = B Q$ (From equation (iv))

So, $Δ APS ≅ Δ BPQ$ (By SAS congruency)

$\Rightarrow PS = PQ$ (By C.P.C.T.).........(v)

According to the equation (iii) and (v),

We get that PQRS is a parallelogram.

$\Rightarrow PS = PQ$

$\Rightarrow$ Two adjacent sides are equal.

Therefore, PQRS is a rhombus.

7. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (See figure). Show that the line segments AF and EC trisect the diagonal BD.

Ans: According to the question,

$E$ and $F$ are the mid-points of AB and CD respectively.

So, $AE = \frac{1}{2} AB$ and $CF = \frac{1}{2} CD \dots \dots \dots .$ (i)

But $ABCD$ is a parallelogram.

So, $AB = CD$ and

$\Rightarrow \frac{1}{2} AB = \frac{1}{2} CD$ and

$\Rightarrow AE = FC$ and (From equation (i))

AECF is a parallelogram.

(FP is a part of $FA$ and $CQ$ is a part of $CE$ ) .........(ii)

Because a segment traced at the midpoint of one of a triangle's sides and parallel to the other side bisects the third.

In $Δ DCQ, F$ is the mid-point of $CD$ and

So, $P$ is the mid-point of DQ.

$\Rightarrow DP = PQ \dots \dots \dots$ ..(iii)

Similarly, In $Δ ABP, E$ is the mid-point of $AB$ and AP

So, $Q$ is the mid-point of BP.

$\Rightarrow BQ = PQ \dots \dots \dots$ .(iv)

Acccording to the equations (iii) and (iv),

$DP = PQ = BQ \dots \dots \dots$ .(v)

Now $BD = BQ + PQ + DP = BQ + BQ + BQ = 3 BQ$

$\Rightarrow BQ = \frac{1}{3} BD \dots \dots \dots$ (vi)

According to the equations (v) and (vi),

$DP = PQ = BQ = \frac{1}{3} BD$

$\Rightarrow$ Points P and trisects BD.

So AF and CE trisects BD.

8. $ABC$ is a triangle right angled at $C$ . A line through the mid-point M of hypotenuse $AB$ and parallel to BC intersects AC at D.

Ans: (i) In $Δ ABC, M$ is the mid-point of $AB$ (According to the question)

So, $A D = D C$ (Converse of mid-point theorem)

Hence $D$ is the mid-point of $AC$ .

$${\text{ABC}}$ is a triangle right angled at ${\text{C}}$. A line through the mid-point M of hypotenuse ${\text{AB}}$ and parallel to BC intersects AC at D$

(ii) (given) consider AC as a transversal.

So, $∠ 1 = ∠ C$ (Corresponding angles)

$\Rightarrow ∠ 1 = 90^{\circ} (∠ C = 90^{\circ})$

Hence, $MD ⊥ AC$ .

(iii) In $△ A M D$ and $△ C M D$ ,

$AD = DC$ (Proved above)

$∠ 1 = ∠ 2 = 90^{\circ}$ (Proved above)

$MD = MD$ (Common)

So, $Δ AMD ≅ Δ CMD$ (By SAS congruency)

$\Rightarrow AM = CM$ (By C.P.C.T.)..........(i)

According to the question $M$ is the mid-point of $AB$ .

So, $AM = \frac{1}{2} AB \dots \dots \dots$ .(ii)

According to the equations (i) and (ii),

$CM = AM = \frac{1}{2} AB$

9. In a parallelogram ABCD, bisectors of adjacent angles $A$ and $B$ intersect each other at P. prove that $∠ A P B = 90^{\circ}$

Ans: According to the question,

$ABCD$ is a parallelogram is and bisectors of $∠ A$ and $∠ B$ intersect each other at P.

$parallelogram ABCD, bisectors of adjacent angles ${\text{A}}$ and ${\text{B}}$ intersect each other at P$

To prove:

$∠ A P B = 90^{\circ}$

Proof:

$∠ 1 + ∠ 2 = \frac{1}{2} ∠ A + \frac{1}{2} ∠ B$

$= \frac{1}{2} (∠ A + ∠ B) \to (i)$

But $ABCD$ is a parallelogram and

So, $∠ A + ∠ B = 180^{\circ}$

So, $∠ 1 + ∠ 2 = \frac{1}{2} \times 180^{\circ} = 90^{\circ}$

In $△ A P B$

$∠ 1 + ∠ 2 + ∠ A P B = 180^{\circ}$

$90^{\circ} + ∠ A P B = 180^{\circ}$

$∠ A P B = 90^{\circ}$

Hence Proved.

10. In figure diagonal AC of parallelogram ABCD bisects $∠ A$ show that

(i) if bisects $∠ C$

ABCD is a rhombus

$diagonal AC of parallelogram ABCD bisects $\angle A$$

Ans: (i) $A B ∥ D C$ and $AC$ is transversal

So, $∠ 1 = ∠ 2$ (Alternate angles)

And $∠ 3 = ∠ 4$ (Alternate angles)

But, $∠ 1 = ∠ 3$

So, $∠ 2 = ∠ 4$

So, $A C$ bisecsts $∠ C$

$diagonal AC of parallelogram ABCD bisects $\angle A$$

(ii) In $△ A B C$ and $△ A D C$

$AC = AC$ (Common)

$∠ 1 = ∠ 3$ (Given)

$∠ 2 = ∠ 4$ (Proved)

So, $△ A B C ≅ △ A D C$

So, $A B = A D$ (By CPCT)

So, $A B C D$ is a rhombus.

11. In figure ABCD is a parallelogram. AX and CY bisects angles $A$ and $C$ . Prove that AYCX is a parallelogram.

$ABCD is a parallelogram. AX and CY bisects angles ${\text{A}}$ and ${\text{C}}$.$

Ans: According to the question,

In a parallelogram AX and CY bisects $∠ A$ and $∠ C$ respectively and we have to

show that AYCX in a parallelogram.

In $Δ A D X$ and $Δ C B Y$

$∠ D = ∠ B \dots$ ..(i) (Opposite angles of parallelogram)

$∠ D A X = \frac{1}{2} ∠ A$ (Given) ...(ii)

And $∠ BCY = \frac{1}{2} ∠ C$ (Given) .....(iii)

But $∠ A = ∠ C$

By equations (2) and (3), we get

$∠ D A X = ∠ B C Y \to (i v)$

Also, $A D = B C$ (opposite sides of parallelogram) ....(v)

According to the equations (i), (iv) and (v), we get

$Δ A D X ≅ Δ C B Y$ (By ASA)

So, $D X = B Y$ (By CPCT)

But, $A B = C D$ (opposite sides of parallelogram)

$AB - BY = CD - DX$

$AY = CX$

But is

So, $A Y C X$ is a parallelogram.

12. Prove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.

Ans: According to the question,

$Δ ABC$ in which $E$ and $F$ are mid points of side $AB$ and $AC$ respectively.

To prove:

$EF ∥ BC$

Construction:

Produce EF to D such that $EF =$ FD. Join CD

Proof: In $△ A E F$ and $Δ C D F$

line segment joining the mid-points of two sides of a triangle is parallel to the third side

$AF = FC (B e c a u s e, F$ is mid-point of AC)

$∠ 1 = ∠ 2$ (Vertically opposite angles)

EF=FD (By construction)

So, $Δ A E F ≅ Δ C D F$ (By SAS)

And So, $A E = C D$ (By CPCT)

$AE = BE (B e c a u s e, E$ is the mid-point)

And So, $B E = C D$

So, $B C D E$ is a parallelogram.

Hence proved.

13. Prove that a quadrilateral is a rhombus if its diagonals bisect each other at right angles.

Ans: Let $ABCD$ be a quadrilateral, where diagonals bisect each other

$∴ OA = OC$

-.- ( 1 $)$

And $OB = OD$ -.-- $(2)$

And they bisect at right angles

$∴ ∠ AOB = ∠ BOC = ∠ COD = ∠ AOD = 90^{\circ}$

In $△ AOD$ and $△ COD$ ,

$OA = OC ($ From $(1))$

$∠ AOD = ∠ COD ($ From $(3))$

$OD = OD ($ Common side $)$

$∴ △ AOD ≅ △ COD ($ SAS congruence rule $)$

$\Rightarrow AD = CD \dots - (4) (CPCT)$

Similarly, we can prove that

$AD = AB$ and $AB = BC \dots$

From (4) and ( 5 $)$

$\Rightarrow AD = CD = AB = BC$

In quadrilateral $ABCD$ ,

$AB = CD$ and $AD = BC$

Both pairs of opposite sides are equal $∴ ABCD$ is a parallelogram.

Also, $AB = CD = AD = BC$

All sides of parallelogram $ABCD$ are equal $∴ ABCD$ is a rhombus.

14. Prove that the straight line joining the mid points of the diagonals of a trapezium is parallel to the parallel sides.

Ans: To prove $M N ‖ A B ‖ C D$

Construction Join $C N$ and produce it to meet $A B$ at $E$ .

In $△ C D N$ and $△ E B N$ , we have

$\begin{array}{lrr} D N & = B N & (since, N is the mid-point of B D) \\ ∠ D C N & = ∠ B E N & (alternate interior angles) \\ and & ∠ C D N & = ∠ E B N & (alternate interior angles) \\ ∴ & Δ C D N & ≅ Δ E B N & (by AAS congruence rule) \\ ∴ & D C & = E B and C N = N E & (by CPCT rule) \end{array}$

Thus, in $Δ C A E$ , the points $M$ and $N$ are the mid-points of $A C$ and $C E$ , respectively.

$∴$ $\Rightarrow$ $M N ‖ A E$

$M N ‖ A B ‖ C D$ (by mid-point theorem) Hence proved

15. In fig $∠ B$ is a right angle in $△ A B C D$ is the mid-point of intersects $BC$ at $E$ . show that

(i) $E$ is the mid-point of $BC$

(ii) $DE ⊥ BC$

(iii) $BD = AD$

$$\vartriangle ABCD$ is the mid-point of intersects ${\text{BC}}$ at ${\text{E}}$.$

Ans:

Proof:

So, and $D$ is mid points of $AC$

In $Δ D C E$ and $Δ D B E$

$CE = BE$

$DE = DE$

And $∠ D E C = ∠ D E B = 90^{\circ}$

So, $Δ D C E = Δ D B E$

So, $Δ D C E ≅ Δ D B E$

So, $C D = B D$

16. ABC is a triangle and through vertices A, B and C lines are drawn parallel to BC, AC and $AB$ respectively intersecting at D, E and $F$ . Prove that perimeter of $Δ D E F$ is double the perimeter of $△ A B C$ .

$ABC is a triangle and through vertices A, B and C lines are drawn parallel to BC, AC and ${\text{AB}}$$

Ans: According to the figure,

$B C A F$ is a parallelogram

So, $B C = A F$

According to the figure,

$A B C E$ is a parallelogram

So, $B C = A E$

$A F + A E = 2 B C$

Or $E F = 2 B C$

Similarly,

$ED = 2 AB$ and $FD = 2 AC$

Because, Perimeter of $Δ A B C = A B + B C + A C$

Perimeter of $Δ D E F = D E + E F + D F$

$= 2 AB + 2 BC + 2 AC$

$= 2 (AB + BC + AC)$

$= 2$ Perimeter of $Δ A B C$

Hence Proved.

17. In fig ABCD is a quadrilateral P, Q, R and S are the mid Points of the sides $AB, BC, CD$ and $DA, AC$ is diagonal. Show that

(i) $SR | | AC$

(ii) $PQ = SR$

(iii) PQRS is a parallelogram

(iv) PR and Sbisect each other

$ABCD is a quadrilateral P, Q, R and S are the mid Points of the sides ${\text{AB}},{\text{BC}},{\text{CD}}$ and ${\text{DA,}}\,{\text{AC}}$ is diagonal.$

Ans: In $Δ ABC, P$ and $Q$ are the mid-points of the sides $AB$ and $BC$ respectively

(i) So, $PQ | | AC$ and $PQ = \frac{1}{2} AC$

(ii) Similarly $SR | | AC$ and $SR = \frac{1}{2} AC$

So, $P Q | | S R$ and $P Q = S R$

(iii) Therefore, PQRS is a Parallelogram.

Because, $P Q ∥ S R$ .

(iv) PR and Sbisect each other.

Because, $P Q ∥ S R$ .

If we meet point P to R and point S to they bisect each other.

18. In $Δ A B C, D, E, F$ are respectively the mid-Points of sides $AB, DC$ and $CA$ . show that $△ A B C$ is divided into four congruent triangles by Joining D,E,F.

Ans: According to the question,

D and $E$ are mid-Points of sides $AB$ and BC of $Δ ABC$

$$\Delta ABC,D,E,F$ are respectively the mid-Points of sides ${\text{AB}},{\text{DC}}$ and ${\text{CA}}$.$

So, $DE | | AC$ {Because a line segment joining the mid-Point of any two sides of a triangle parallel to third side $}$

Similarly, $DF ∥ BC$ and $EF | | AB$

ADEF, BDEF and DFCE are all Parallelograms.

DE is diagonal of Parallelogram BDFE

$Δ B D E ≅ Δ F E D$

Similarly, $Δ DAF ≅ Δ FED$

And $Δ EFC ≅ Δ FED$

So all triangles are congruent

19. ABCD is a Parallelogram is which P and are mid-points of opposite sides AB and CD. If Aintersect DP at S, Bintersects $CP$ at $R$ , show that

(i) APCis a Parallelogram

(ii) DPBis a parallelogram

(iii) PSQR is a parallelogram

Ans: (i) In quadrilateral APCQ

$AP | | QC (B e c a u s e, AB | | CD) \dots \dots \dots$ (i)

$AP = \frac{1}{2} AB, CQ = \frac{1}{2} CD$ (Given)

Also $AB = CD$

So $AP = QC \dots \dots \dots$ ...(ii)

Therefore, APCis a parallelogram

(If any two sides of a quadrilateral equal and parallel then quad is a parallelogram)

(ii) Similarly, quadrilateral DPBis a Parallelogram because $DQ ∥ PB$ and $DQ = PB$

(iii) In quadrilateral PSQR,

$SP ∥ QR$ (SP is a part of DP and QR is a Part of QB)

Similarly, $SQ ∥ PR$

So, PSQR is also parallelogram.

20. l, m, n are three parallel lines intersected by transversals P and such that l, m and $n$ cut off equal intercepts $AB$ and $BC$ on $P$ .In fig Show that l, m, n cut off equal intercepts DE and EF on also.

$l, m, n are three parallel lines intersected by transversals P and such that l, m and $n$ cut off equal intercepts ${\text{AB}}$ and ${\text{BC}}$ on ${\text{P}}$$

Ans: In fig l, m, n are 3 parallel lines intersected by two transversal $P$ and $Q$ .

To Prove:

$DE = EF$

Proof:

In $Δ A C F$

$B$ is mid-point of $AC$

And $BG ∥ CF$

So, $G$ is mid-point of AF (By mid-point theorem)

Now In $Δ A F D$

$G$ is mid-point of $AF$ and $GE ∥ AD$ .

So, $E$ is mid-point of FD (By mid-point theorem)

So, $DE = EF$

Hence Proved.

21. ABCD is a parallelogram in which $E$ is mid-point of AD. $DF ∥ EB$ meeting AB produced at $F$ and $BC$ at $L$ prove that $DF = 2 DL$

$ABCD is a parallelogram in which $E$ is mid-point of AD. ${\text{DF}}\parallel {\text{EB}}$ meeting AB produced at ${\text{F}}$ and ${\text{BC}}$ at ${\text{L}}$$

Ans: In $△ A F D$

Because, $E$ is mid-point of AD (According to the question)

$BE | | DF$ (According to the question)

So, by converse of mid-point theorem B is mid-point of AF

So, $A B = B F \dots . (i)$

$ABCD$ is parallelogram

So, $A B = C D \dots \dots (i i)$

According to the equation (i) and (ii)

$CD = BF$

Consider $Δ D L C$ and $Δ F L B$

$DC = FB$ (Proved above)

$∠ D C L = ∠ F B L$ (Alternate angles)

$∠ D L C = ∠ F L B$ (Vertically opposite angles)

$Δ D L C = Δ F L B$ (By ASA)

So, $DL = LF$

So, $DF = 2 DL$

Hence proved.

22. PQRS is a rhombus if $∠ P = 65^{\circ}$ find $∠ R S Q$ .

$PQRS is a rhombus if $\angle P = {65^\circ }$$

Ans: According to the question and figure,

$∠ R = ∠ P = 65^{\circ}$ (Opposite angles of a parallelogram are equal)

Suppose, $∠ R S Q = x^{\circ}$

In $△ R S Q$

We have $RS = RQ$

$∠ R Q S = ∠ R S Q = x^{\circ}$ (Opposite Sides of equal angles are equal)

In $△ R S Q$

$∠ S + ∠ Q + ∠ R = 180^{\circ}$ (By angle sum property)

$x^{\circ} + x^{\circ} + 65^{\circ} = 180^{\circ}$

$2 x^{\circ} = 180^{\circ} - 65^{\circ}$

$2 x^{\circ} = 115^{\circ}$

$x = \frac{115}{2} = {57.5}^{\circ}$

Hence, the value of $∠ R S Q = {57.5}^{\circ}$ .

23. $ABCD$ is a trapezium in which $AB | | CD$ and $AD = BC$ show that

(i) $∠ A = ∠ B$

(ii) $∠ C = ∠ D$

(iii) $△ A B C ≅ Δ B A D$

${\text{ABCD}}$ is a trapezium in which ${\text{AB}}||{\text{CD}}$ and ${\text{AD}} = {\text{BC}}$

Ans: (i) Produce $AB$ and Draw a line Parallel to DA meeting at $E$

Because, $A D | | E C$

$∠ 1 + ∠ 3 = 180^{\circ} \dots .$ (1) (We know that the sum of interior angles on the some side of transversal is $180^{\circ}$ )

In $Δ B E C$

BC=CE (given)

So, $∠ 3 = ∠ 4$ .....(2) (In a triangle equal side to opposite angles are equal)

$∠ 2 + ∠ 4 = 180^{\circ} \dots \dots . (3)$

By equation (1) and (3)

$∠ 1 + ∠ 3 = ∠ 2 + ∠ 4$

$∠ 3 = ∠ 4$

So, $∠ 1 = ∠ 2$

So, $∠ A = ∠ B$

(ii) Because,

$∠ D + ∠ 6 + ∠ 5 = 180^{\circ} \dots \dots (i)$

$∠ 6 + ∠ 5 + ∠ 3 = 180^{\circ} \dots \dots . (i i)$

$∠ D + ∠ 6 + ∠ 5 = ∠ 6 + ∠ 5 + ∠ 3$

$∠ D = ∠ 3 = ∠ 4$

So, $∠ C = ∠ D$ .

(iii) In $Δ ABC$ and $Δ BAD$

$AB = AB$ (common)

$∠ 1 = ∠ 2$ (Proved above)

$AD = BC$ (According to the question)

So, $Δ A B C ≅ Δ B A D$ (By SAS)

24. Show that diagonals of a rhombus are perpendicular to each other.

Ans:

According to the figure,

A rhombus ABCD whose diagonals AC and BD intersect at a Point O.

To Prove:

$∠ B O C = ∠ D O C = ∠ A O D = ∠ A O B = 90^{\circ}$

Proof:

Clearly ABCD is a Parallelogram in which

$AB = BC = CD = DA$

As we know that diagonals of a Parallelogram bisect each other

So, $OA = OC$ and $OB = OD$

Now in $Δ BOC$ and $Δ DOC$ , we have

$OB = OD$

$BC = DC$

$OC = OC$

So, $Δ BOC ≅ Δ DOC$ (By SSS)

So, $∠ B O C = ∠ D O C$ (By C.P.C.T)

But $∠ B O C + ∠ D O C = 180^{\circ}$

So, $∠ B O C = ∠ D O C = 90^{\circ}$

Similarly, $∠ A O B = ∠ A O D = 90^{\circ}$

Therefore, diagonals of a rhombus bisect each other at $90^{\circ}$ .

25. Prove that the diagonals of a rhombus bisect each other at right angles.

Ans: According to the question and figure given a rhombus ABCD whose diagonals AC and BD intersect each other at $O$ .

As we need to prove that $OA = OC, OB = OD$ and $∠ A O B = 90^{\circ}$

In $△ A O B$ and $Δ C O D$

$AB = CD$ (Sides of rhombus)

$∠ A O B = ∠ C O D$ (Vertically opposite angles)

And $∠ A B O = ∠ C D O$ (Alternate angles)

So, $Δ AOB ≅ Δ COD$ (By ASA)

So, $OA = OC$

And $OB = OD$ (By C.P.C.T)

Also in $Δ AOB$ and $Δ COB$

OA=OC (Proved)

$AB = CB$ (Sides of rhombus)

And $OB = OB$ (Common)

$Δ AOB ≅ Δ COB$ (By SSS)

So, $∠ A O B = ∠ C O B$ (By C.P.C.T)

But $∠ A O B + ∠ C O B = 180^{\circ}$ (linear pair)

So, $∠ A O B = ∠ C O B = 90^{\circ}$

Hence proved.

26. In fig $ABCD$ is a trapezium in which $AB | | DC$ and $AD = BC .$ Show that $∠ A = ∠ B$

${\text{ABCD}}$ is a trapezium in which ${\text{AB}}||{\text{DC}}$ and ${\text{AD}} = {\text{BC}}.$

Ans: To show that $∠ A = ∠ B$ ,

Draw $CP ∥ DA$ meeting $AB$ at $P$

Because, $AP | | DC$ and $CP | | DA$

So, $APCD$ is a parallelogram

Again in ∆ CPB

$CP = CB (B e c a u s e, BC = AD)$ (Given)

$∠ C P B = ∠ C B P \dots (i)$ (Angles opposite to equal sides)

But $∠ C P A + ∠ C P B = 180^{\circ} ($ By linear pair)

Also $∠ A + ∠ C P A = 180^{\circ} (B e c a u s e, APCD$ is a parallelogram)

So, $∠ A + ∠ C P A = ∠ C P A + ∠ C P B$ Or $∠ A = ∠ C P B$

$= ∠ CB$

Hence proved.

27. In fig ABCD and ABEF are Parallelograms, prove that CDFE is also a parallelogram.

Ans: According to the question,

$A B C D$ is a parallelogram

So, $AB = DC also AB | | DC \dots \dots \dots \dots . . (i)$

Also ABEF is a parallelogram

Because, $AB = FE$ and $AB | | FE \dots \dots \dots$ ..(ii)

By equations (i) and (ii)

$AB = DC = FE$

So, $AB = FE$

And $AB | | DC | | FE$

So, $AB | | FE$

So, CDEF is a parallelogram.

Hence Proved.

4 Marks Questions

1. ABCD is a rectangle in which diagonal AC bisects $∠ A$ as well as $∠ C$ . Show that:

(i) ABCD is a square.

(ii) Diagonal BD bisects both $∠ B$ as well as $∠ D$ .

$ABCD is a rectangle in which diagonal AC bisects $\angle {\text{A}}$ as well as $\angle {\text{C}}$.$

Ans: According to the question,

$ABCD$ is a rectangle.

Hence $AB = DC$ .........(i)

And $BC = AD$

Also $∠ A = ∠ B = ∠ C = ∠ D = 90^{\circ}$

(i) In $Δ ABC$ and $Δ ADC$

$∠ 1 = ∠ 2$ and $∠ 3 = ∠ 4$

(AC bisects $∠ A$ and $∠ C$ (According to the question))

$AC = AC$ (Common)

So, $Δ ABC ≅ Δ ADC$ (By ASA congruency)

$\Rightarrow AB = AD \dots \dots \dots . .$ (ii)

According to the equations (i) and (ii),

$AB = BC = CD = AD$

Therefore, $ABCD$ is a square.

(ii) In $Δ ABC$ and $Δ ADC$

$\Delta {\text{ABC}}$ and $\Delta {\text{ADC}}$

$AB = BA$ (Since $ABCD$ is a square)

$AD = DC$ (Since $ABCD$ is a square)

$BD = BD$ (Common)

So, $Δ ABD ≅ Δ CBD$ (By SSS congruency)

$\Rightarrow ∠ ABD = ∠ CBD$ (By C.P.C.T.) ..........(iii)

And $∠ ADB = ∠ CDB$ (By C.P.C.T.) ...........(iv)

According to the equations (iii) and (iv),

It is clear that diagonal BD bisects both $∠ B$ and $∠ D$ .

2. An $Δ ABC$ and and . Vertices $A, B$ and $C$ are joined to vertices D, E and F respectively (See figure). Show that:

(i) Quadrilateral ABED is a parallelogram.

(ii) Quadrilateral BEFC is a parallelogram.

(iii) and $AD = CF$

(iv) Quadrilateral ACFD is a parallelogram.

(v) $AC = DF$

(vi) $Δ ABC ≅ Δ DEF$

$$\Delta {\text{ABC}}$ and and . Vertices ${\text{A}},{\text{B}}$ and ${\text{C}}$ are joined to vertices D, E and F respectively$

Ans: (i) In $Δ ABC$ and $Δ DEF$

$AB = DE$ (According to the question)

And $AB ∥ DE$ (According to the question)

So, ABED is a parallelogram.

(ii) In $Δ ABC$ and $Δ DEF$

$BC =$ EF (According to the question)

And $BC ∥ EF$ (According to the question)

So, BEFC is a parallelogram.

(iii) As ABED is a parallelogram.

So, and $AD = BE$ ..........(i)

Also BEFC is a parallelogram.

So, and $CF = BE \dots \dots \dots .$ (ii)

According to the equations (i) and (ii), we get

So, and $AD = CF$

(iv) As and $AD = CF$

$\Rightarrow$ ACFD is a parallelogram.

(v) As ACFD is a parallelogram.

So, $AC = DF$

(vi) In $Δ ABC$ and $Δ DEF$ ,

$AB = DE$ (According to the question)

$BC = EF$ (According to the question)

$AC = DF$ (Proved)

So, $Δ ABC ≅ Δ DEF$ (By SSS congruency)

3. ABCD is a trapezium, in which is a diagonal and $E$ is the mid-point of AD. A line is drawn through E, parallel to AB intersecting BC at F (See figure). Show that $F$ is the mid-point of BC.

$ABCD is a trapezium, in which is a diagonal and ${\text{E}}$ is the mid-point of AD. A line is drawn through E, parallel to AB intersecting BC at F$

Ans: Suppose diagonal BD intersect line EF at point P.

In $Δ DAB$ ,

E is the mid-point of AD and (According to the question) $P$ is the part of EF)

So, $P$ is the mid-point of other side, $BD$ of $Δ DAB$ .

(A line drawn parallel to one side of a triangle and through the mid-point of the other intersects the third side at the mid-point.)

Now in $Δ BCD$ ,

P is the mid-point of BD and (according to the question) and $A B ∥ D C$ (according to the question))

So, and PF is a part of $EF$ .

So, $F$ is the mid-point of other side, BC of $Δ BCD$ . (Converse of mid-point of theorem)

4. Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.

Ans: According to the question and figure,

A quadrilateral ABCD in which EG and FH are the line-segments joining the midpoints of opposite sides of a quadrilateral.

To prove:

EG and FH bisect each other.

Construction:

Join AC, EF, FG, GH and HE.

Proof:

In $Δ ABC, E$ and $F$ are the mid-points of respective sides $AB$ and $BC$ .

So, and $EF = \frac{1}{2} AC \dots \dots \dots$ .. (i)

Similarly, in $Δ$ ADC,

G and $H$ are the mid-points of respective sides $CD$ and $AD$ .

So, and $HG = \frac{1}{2} AC \dots \dots \dots .$ (ii)

According to the equations (i) and (ii),

and $EF = HG$

So, EFGH is a parallelogram.

Line segments (i.e. diagonals) EG and FH (of parallelogram EFGH) bisect each other because the diagonals of a parallelogram bisect each other.

5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Ans: Suppose $ABCD$ be a quadrilateral in which equal diagonals AC and BD bisect each other at right angle at point $O$ .

We have $AC = BD$ and $OA = OC$

And $OB = OD \dots \dots \dots$ ..(ii)

Now $OA + OC = OB + OD$

$\Rightarrow OC + OC = OB + OB$ (Using equation (i) and (ii))

$\Rightarrow 2 OC = 2 OB$

$\Rightarrow OC = OB \dots \dots \dots . .$ (iii)

According to the equations (i), (ii) and (iii),

we get,

$O A = O B = O C = O D$ ..........(iv)

Now in $Δ AOB$ and $Δ COD$ ,

$OA =$ OD (Proved)

$∠ AOB = ∠ COD$ (Vertically opposite angles)

$OB = OC$ (Proved)

So, $Δ AOB ≅ Δ DOC$ (By SAS congruency)

$\Rightarrow AB = DC$ (By C.P.C.T.) ..........(v)

Similarly,

$Δ BOC ≅ Δ AOD$ (By SAS congruency)

$\Rightarrow BC = AD$ (By C.P.C.T.) ..........(vi)

According to the equation (v) and (vi), it is determined that $ABCD$ is a parallelogram because opposite sides of a quadrilateral are equal.

Now in $Δ ABC$ and $Δ BAD$ ,

$AB = BA$ (Common)

$BC = AD$ (Proved above)

$AC = BD$ (According to the figure)

So, $Δ ABC ≅ Δ BAD$ (By SSS congruency)

$\Rightarrow ∠ ABC = ∠ BAD$ (By C.P.C.T.) $\dots \dots \dots . .$ (vii)

But $∠ ABC + ∠ BAD = 180^{\circ} (ABCD$ is a parallelogram) ..........(viii)

So, and $AB$ is a transversal.

$\Rightarrow ∠ ABC + ∠ ABC = 180^{\circ}$ (Using equations (vii) and (viii))

$\Rightarrow 2 ∠ ABC = 180^{\circ} \Rightarrow ∠ ABC = 90^{\circ}$

So, $∠ ABC = ∠ BAD = 90^{\circ} \dots \dots \dots$ (ix)

Opposite angles of a parallelogram are equal.

But $∠ ABC = ∠ BAD =$

So, $∠ ABC = ∠ ADC = 90^{\circ} \dots \dots \dots . (x)$

So, $∠ BAD = ∠ BDC = 90^{\circ} \dots \dots \dots . (xi)$

According to the equations (x) and (xi), we get

$∠ ABC = ∠ ADC = ∠ BAD = ∠ BDC = 90^{\circ} \dots \dots \dots . . (xii)$

Now in $Δ AOB$ and $Δ BOC$ ,

$OA = OC$ (Given)

$∠ AOB = ∠ BOC = 90^{\circ}$ (Given)

$OB = OB$ (Common)

So, $Δ AOB ≅ Δ COB$ (By SAS congruency)

$\Rightarrow AB = BC \dots \dots \dots$ .(xiii)

According to the equations (v), (vi) and (xiii), we get,

$AB = BC = CD = AD \dots \dots \dots . . (xiv)$

Now, according to the equations (xii) and (xiv), we have a quadrilateral whose equal diagonals bisect each other at right angle.

Also sides are equal make an angle of $90^{\circ}$ with each other.

So, ABCD is a square.

6. $ABCD$ is a trapezium in which and $AD = BC$ (See figure). Show that:

(i) $∠ A = ∠ B$

(ii) $∠ C = ∠ D$

(iii) $Δ ABC ≅ Δ BAD$

(iv) Diagonal AC = Diagonal BD

${\text{ABCD}}$ is a trapezium in which and ${\text{AD}} = {\text{BC}}$

Ans: According to the question,

$ABCD$ is a trapezium.

and $AD = BC$

To prove:

(i) $∠ A = ∠ B$

(ii) $∠ C = ∠ D$

(iii) $Δ ABC ≅ Δ BAD$

(iv) Diagonal AC = Diagonal BD

Construction:

Draw CE AD and extend AB to intersect CE at $E$ .

$${\text{ABCD}}$ is a trapezium in which and ${\text{AD}} = {\text{BC}}$ AND CE AD and extend AB to intersect CE at $E$.$

Proof:

(i) As AECD is a parallelogram. (By construction)

So, $AD = EC$

But $AD = BC$ (According to the question)

So, $BC = EC$

$\Rightarrow ∠ 3 = ∠ 4$ (Angles opposite to equal sides are equal)

Now $∠ 1 + ∠ 4 = 180^{\circ}$ (Interior angles)

And $∠ 2 + ∠ 3 = 180^{\circ}$ (Linear pair)

$\Rightarrow ∠ 1 + ∠ 4 = ∠ 2 + ∠ 3$

$\Rightarrow ∠ 1 = ∠ 2 (B e c a u s e, ∠ 3 = ∠ 4)$

$\Rightarrow ∠ A = ∠ B$

(ii) $∠ 3 = ∠ C$ (Alternate interior angles)

And $∠ D = ∠ 4$ (Opposite angles of a parallelogram)

But $∠ 3 = ∠ 4$ ( $Δ BCE$ is an isosceles triangle)

So, $∠ C = ∠ D$

(iii) In $Δ ABC$ and $Δ BAD$ ,

$AB = AB$ (Common)

$∠ 1 = ∠ 2$ (Proved)

$AD = BC$ (According to the question)

So, $Δ ABC ≅ Δ BAD$ (By SAS congruency)

$(i v) AC = BD$ (By C.P.C.T.)

7. Prove that if the diagonals of a quadrilateral are equal and bisect each other at right angles then it is a square.

Ans: According to the question and figure,

In a quadrilateral $ABCD, AC = BD, AO = OC$ and $BO = OD$ and $∠ A O B = 90^{\circ}$

To prove:

$ABCD$ is a square.

Proof:

In $△ A O B$ and $Δ C O D$

$OA = OC$

$OB = OD$ (According to the question and figure)

And

$∠ A O B = ∠ C O D$ (Vertically opposite angles)

So, $Δ A O B ≅ Δ C O D$ (By SAS)

So, $A B = C D$ (By C.P.C.T.)

$∠ 1 = ∠ 2$ (By C.P.C.T) But these are alternate angles So,

ABCD is a parallelogram whose diagonals bisects each other at right angles.

So, $A B C D$ is a rhombus

Again in $△ A B D$ and $Δ B C A$

$AB = BC$ (Sides of a rhombus)

$AD = AB$ (Sides of a rhombus)

And $BD = CA$ (Given)

So, $△ A B D ≅ Δ B C A$

So, $∠ B A D = ∠ C B A$ (By CPCT)

These are alternate angles of these same side of transversal

So, $∠ B A D + ∠ C B A = 180^{\circ}$ or $∠ B A D = ∠ C B A = 90^{\circ}$

Therefore, $ABCD$ is a square.

8. Prove that in a triangle, the line segment joining the mid points of any two sides is parallel to the third side.

Ans: According to the question and figure,

A $Δ A B C$ in which D and E are mid-points of the side $AB$ and $AC$ respectively

To Prove: and $D E = \frac{1}{2} B C$

Construction: Draw

Proof: In $△ A D E$ and $Δ C F E$

$∠ 1 = ∠ 2$ (Vertically opposite angles)

$AE = CE$ (Given)

And $∠ 3 = ∠ 4$ (Alternate interior angles)

So, $Δ A D E ≅ Δ C F E$ (By ASA)

So, $DE = FE$ (By C.P.C.T)

But DA = DB

So, $DB = FC$

So, DBCF is a parallelogram

Also $DE = EF = \frac{1}{2} BC$

Hence, and $D E = \frac{1}{2} B C$ .

9. $ABCD$ is a rhombus and P, Q, R, and $S$ are the mid-Points of the sides $AB, BC, CD$ and DA respectively. Show that quadrilateral PQRS is a rectangle.

Ans: Join AC and BD which intersect at O let BD intersect RS at E and AC intersect Rat F

In $Δ ABD, P$ and $S$ are mid-points of sides $AB$ and $AD$ .

$${\text{ABCD}}$ is a rhombus and P, Q, R, and ${\text{S}}$ are the mid-Points of the sides ${\text{AB}},{\text{BC}},{\text{CD}}$ and DA respectively$

So, $PS | | BD$ and $PS = \frac{1}{2} B D$

Similarly, $RQ | | DB$ and $RQ = \frac{1}{2} BD$

So, $RS | | BD | | RQ$ and $PS = \frac{1}{2} B D = R Q$

$PS = RQ$ and $PS | | RQ$

So, PQRS is a parallelogram

Now, $RF ∥ EO$ and $RE ∥ FO$

So, OFRE is also a parallelogram.

Again, we also know that diagonals of a rhombus bisect each other at right angles.

Because, $∠ E O F = 90^{\circ}$

Because, $∠ E O F = ∠ E R F$ (Opposite angles of a parallelogram)

So, $∠ E R F = 90^{\circ}$

So, each angle of the parallelogram PQRS is $90^{\circ}$

Therefore, PQRS is a rectangle.

10. In the given Fig. ABCD is a parallelogram $E$ is mid-point of AB and CE bisects $∠ B C D$ Prove that:

(i) $AE = AD$

(ii) $DE$ bisects $∠ A D C$

(iii) $∠ D E C = 90^{\circ}$

$ABCD is a parallelogram ${\mathbf{E}}$ is mid-point of AB and CE bisects $\angle BCD$$

Ans: According to the question,

$ABCD$ is a parallelogram

So, and EC cuts them

$\Rightarrow ∠ B E C = ∠ E C D$ (Alternate interior angle)

$\Rightarrow ∠ B E C = ∠ E C B (∠ E C D = ∠ E C B)$

$\Rightarrow E B = B C$

$\Rightarrow A E = A D$

(i) Now $AE = AD$

$\Rightarrow ∠ A D E = ∠ A E D$

$\Rightarrow ∠ A D E = ∠ E A C (S o, ∠ A E D = ∠ E D C$ Alternate interior angles)

(ii) So, DE bisects $∠ A D C$

(iii) Now $∠ A D C + ∠ B C D = 180^{\circ}$

$\Rightarrow \frac{1}{2} ∠ A D C + \frac{1}{2} ∠ B C D = 90^{\circ}$

$\Rightarrow ∠ E D C + ∠ D C E = 90^{\circ}$

But, the sum of all the angles of the triangle is $180^{\circ}$

$\Rightarrow 90^{\circ} + ∠ D E C = 180^{\circ}$

$\Rightarrow ∠ D E C = 90^{\circ}$

Hence proved.

11. ABC is a triangle right angled at $C$ . A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. show that

(i) $D$ is mid-point of $AC$

(ii) $MD ⊥ AC$

(iii) $CM = MA = \frac{1}{2} AB$

$ABC is a triangle right angled at ${\mathbf{C}}$. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D$

Ans: According to the question,

$ABC$ is a triangle right angle at $C$

(i) $M$ is mid-point of $AB$

And $MD ∥ BC$

So, $D$ is mid-Point of $AC$ (a line through midpoint of one side of a triangle parallel to another side bisect the third side)

(ii) Because, $MD | | BC$

$∠ A D M = ∠ D C B$ (Corresponding angles)

$∠ A D M = 90^{\circ}$

(iii) In $Δ A D M$ and $Δ C D M$

$AD = DC$ (Because D is mid-point of $AC)$

$DM = DM$ (Common)

So, $Δ ADM ≅ Δ CDM$ (By SAS)

$AM = CM$ (By C.P.C.T)

$AM = CM = MB$ (Because M is mid-point of $AB)$

So, $CM = MA = \frac{1}{2} AB$

Hence proved.

Download Important Questions Of Chapter 8 Maths Class 9 PDF

Let’s Learn About Quadrilateral and Its Type

Definition of Quadrilateral

Quadrilateral derived from two words, i.e quad means four and lateral means sides. Any closed figures which are having four sides are called quadrilaterals. The sides of the quadrilateral may be equal, unequal, parallel, or irregular shapes.

Types of Quadrilaterals

Based on angles and side lengths, there are various types of quadrilaterals:

Parallelogram
Rectangle
Square
Rhombus
Trapezium
Kite

Parallelogram - A parallelogram is a quadrilateral which has opposite sides parallel. In a parallelogram, all the opposite sides are equal and the angles made by each opposite side are also equal. In the figure shown below, PQRS is a quadrilateral and since PQ || RS and PS || QR we call it a parallelogram.

Rectangle - Rectangle is also a type of parallelogram with a little difference in the angles of the sides. All the sides of the rectangle are at the right angle or to say perpendicular to each other. The figure below shows a quadrilateral ABCD. Since all its sides are parallel to each other, we may also call it a type of parallelogram with line segments placed at the right angle to each other. Mathematically represented as AB || CD and AC || BD. ∠A =∠B =∠C=∠D= 90°.

Square - A square is a quadrilateral with all four sides equal. All the vertex of a square makes a right angle with its sides. Suppose WXYZ is a square which shows the following characteristic:

WX || YZ and WY || XZ. ∠W =∠X =∠Y=∠Z= 90°

Rhombus - A rhombus is also a parallelogram which has all sides equal. In other words, a parallelogram that shows resemblance to a square with respect to its length of sides is called a rhombus. These are sometimes referred to as Diamonds also. Rhombus shows a very important feature regarding their diagonals. The diagonals of a rhombus meet exactly in the middle at a right angle and are also bisect with each other.

In the figure above, we can see that STUV is a quadrilateral with sides ST || UV and SV || TU. All the sides of a rhombus are equal, thus ST=TU=UV=VS which also happen to form equal angles.

Trapezium - Among all the other types of quadrilaterals, a trapezium shows different characteristics. In a trapezium, all the sides may not be equal but one of the pairs of sides has to be parallel to each other.

In the above figure, ABCD is a trapezium with sides AB || DC. A trapezium is also known as an irregular quadrilateral because it does not show similarity in lengths and angles of sides.

Kite - A kite is a quadrilateral which has two pairs of equal-length sides and these sides are adjacent to each other. The pair of adjacent sides of a kite are of equal length.

Important Formulas and Properties for Class 9 Maths Chapter 8 Quadrilaterals

Concept	Formula/Property
Angle Sum Property of a Quadrilateral	Sum of all interior angles of a quadrilateral = $360^{\circ}$ .
Area of a Parallelogram	$t Base \times Height$
Area of a Rhombus	$\frac{1}{2} \times Diagonal 1 \times Diagonal 2$
Midpoint Theorem	The line joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
Diagonal Bisect Property of Parallelogram	Diagonals of a parallelogram bisect each other.

Benefits of Class 9 Maths Chapter 8 Quadrilaterals Important Questions

Comprehensive Revision: These important questions cover all the key topics in Chapter 8, ensuring that students thoroughly revise essential concepts like the angle sum property, properties of parallelograms, and various quadrilateral types.
Exam-Focused Preparation: The questions are designed to reflect the CBSE exam pattern, helping students understand the kind of problems they might encounter during exams.
Concept Clarity: Solving these questions enhances understanding of theorems and their applications, strengthening conceptual clarity for better problem-solving.
Improved Time Management: Practising these important questions aids students in improving their speed and accuracy, essential for managing time effectively during exams.
Free Access to Quality Material: The PDF of these important questions is available for free, making it easy for students to access reliable study material anytime and anywhere.

Conclusion

After going through the above Class 9 Maths Chapter 8 important questions, now it will be easier for you to differentiate between them and learn all the important concepts. So, every quadrilateral is a four-sided figure but still, there is a lot of difference between them, depending on the length of sides and the equality of angle. The difference between them is mentioned in their properties, so go through the above properties carefully which will help you to differentiate between every type of quadrilateral. Also, practise Class 9 Maths Chapter 8 extra questions so that you can through the concept and get good marks in the exam.

Related Study Materials for Class 9 Maths Chapter 8 Quadrilaterals

S.No	Study Materials for Class 9 Maths Chapter 8
1.	CBSE Class 9 Maths Quadrilaterals Solutions
2.	CBSE Class 9 Maths Quadrilaterals Notes
3.	CBSE Class 9 Maths Quadrilaterals NCERT Exemplar
4.	CBSE Class 9 Maths Quadrilaterals RD Sharma Solutions
5.	CBSE Class 9 Maths Quadrilaterals RS Aggarwal Solutions
6.	CBSE Class 9 Maths Quadrilaterals Important Formulas

CBSE Class 9 Maths Chapter-wise Important Questions

S.No	Chapter-wise Important Questions for Class 9 Maths
1.	Chapter 1 - Number Systems Questions
2.	Chapter 2 - Polynomials Questions
3.	Chapter 3 - Coordinate Geometry Questions
4.	Chapter 4 - Linear Equations in Two Variables Questions
5.	Chapter 5 - Introduction to Euclid’s Geometry Questions
6.	Chapter 6 - Lines and Angles Questions
7.	Chapter 7 - Triangles Questions
8.	Chapter 9 - Circles Questions
9.	Chapter 10 - Heron’s Formula Questions
10.	Chapter 11 - Surface Areas and Volumes Questions
11.	Chapter 12 - Statistics Questions

FAQs on CBSE Class 9 Maths Important Questions - Chapter 8 Quadrilaterals

1. How do you solve a Class 9 quadrilateral problem?

To solve quadrilateral problems, students need to be thorough with the different types of quadrilaterals first. Then they need to have an idea of all the properties of each of these quadrilaterals. Then the theorems are enough to give them an understanding. Without strengthening the basics, it is extremely difficult to proceed. The Important Questions created for Class 9 Chapter 8 Maths, is an excellent material to help students solve the various proofs and problems given in the chapter as they offer expert simple answers in an easily approachable manner.

2. What is the easiest way to learn Quadrilaterals Class 9?

To learn the chapter of Quadrilaterals, the easiest way would always be to know its various properties. As such, important Questions provides a material where students can focus on the important topics in Chapter 8 that are related to quadrilaterals. Students can download the PDF of these important questions free of cost from the vedantu website (vedantu.com).

Equal opposite angles
Equal opposite sides
Bisecting diagonals
One pair of opposite sides: equal and parallel
Angles give a sum of 360 degrees
Division of diagonals provide two congruent triangles
6 various types of quadrilaterals

3. How many types of quadrilaterals are there in class 9?

Chapter 8 of Class 9 is all about quadrilaterals where students are introduced to various four-sided polygons and their properties. As such, there are a total of 6 kinds of quadrilaterals that are introduced to Class 9 students. The following points state out the quadrilaterals;

Trapezium: a pair of parallel opposite sides
Parallelogram: two pairs of parallel opposite sides
Rectangle: perpendicular angles
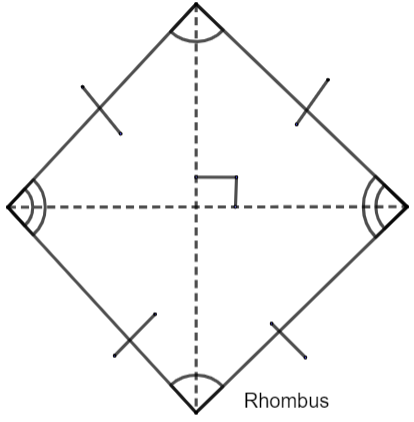
Rhombus: all sides equal
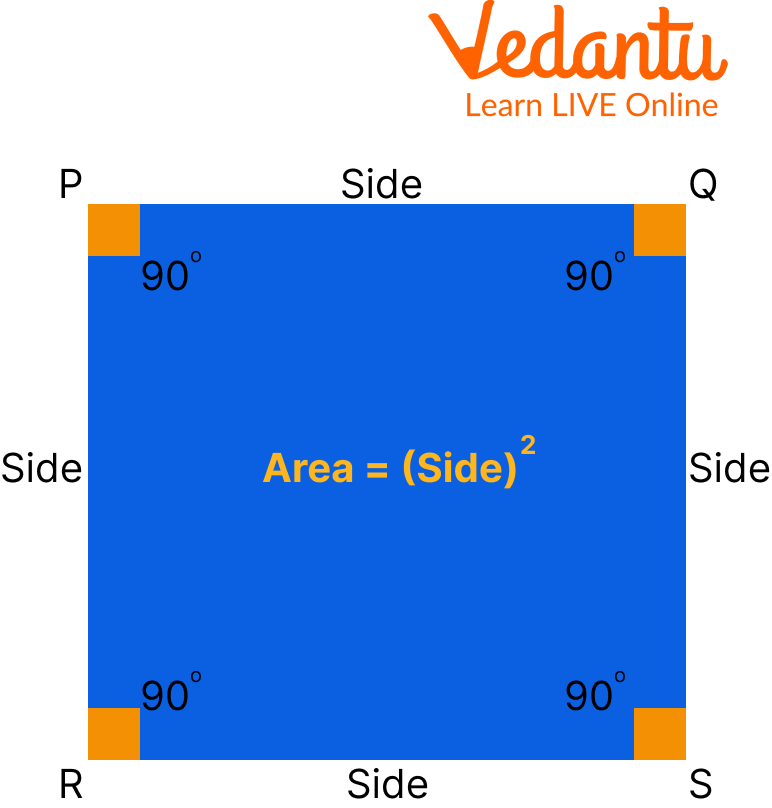
Square: all sides equal with perpendicular angles
Kite: two pairs of adjacent sides

4. What is a quadrilateral in 9th Standard Maths Chapter 8?

When a figure is created by joining four non-collinear elements it is known as a quadrilateral. To understand the concept better, Important Questions help students understand its definition by stating that a quadrilateral is a four-sided polygon, that is, a figure formed by joining collinear points together such that the figure has four sides and four vertices with two diagonals. The angles in the quadrilateral when summed together gives a measure of 360 degrees. Square, rectangle, rhombus, parallelogram, and trapezium are the various four-sided polygons.

5. What are the benefits of using Important Questions for Class 9 Chapter 8 of Maths?

Important questions for Chapter 8 of Class 9 Maths is specifically designed to ensure that students are able to focus on and cover the most important areas from the chapter. The chapter being 'Quadrilaterals', students learn the required types of quadrilaterals and their various properties created by expert teachers in a very simple language. The stepwise explanation of all the topics is an added benefit to the students because they offer tips and techniques to score well for their exams.

6. What is the difference between a parallelogram and a rhombus in Chapter 8 Quadrilaterals?

Both parallelograms and rhombuses are quadrilaterals with opposite sides that are parallel. The key difference is that in a rhombus, all four sides are equal in length, whereas in a parallelogram, opposite sides are equal but not necessarily all four. Additionally, the diagonals of a rhombus intersect at right angles, which is not true for all parallelograms.

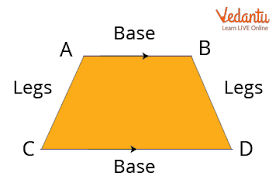
7. What are the properties of a trapezium as mentioned in Class 9 Maths Chapter 8?

A trapezium is a quadrilateral with exactly one pair of parallel sides. Some key properties include:

Non-parallel sides are called legs.
The sum of all interior angles is $360^{\circ}$ .
If the non-parallel sides are equal, the trapezium is called an isosceles trapezium, and its diagonals are also equal.

8. Why is the Angle Sum Property important in solving problems on quadrilaterals?

The Angle Sum Property states that the sum of the interior angles of a quadrilateral is always $360^{\circ}$ . This property is crucial for solving many problems related to angles in quadrilaterals, as it allows students to calculate unknown angles when the other three are known.

9. Can a square be classified as a rectangle or a rhombus in Chapter 8 Quadrilaterals?

Yes, a square can be classified as both a rectangle and a rhombus. A square is a rectangle because all angles are $90^{\circ}$ and opposite sides are equal. It is also a rhombus because all four sides are of equal length, and its diagonals intersect at right angles.

10. How can Important Questions help in mastering Chapter 8 Quadrilaterals?

Important Questions for Chapter 8 Quadrilaterals focus on key concepts, properties, and problem-solving techniques. They provide step-by-step solutions, making it easier for students to understand and apply theorems. These questions also cover various problem types, helping students practice effectively and improve exam performance.

11. What is the role of diagonals in identifying quadrilateral properties?

Diagonals play a significant role in determining the properties of a quadrilateral:

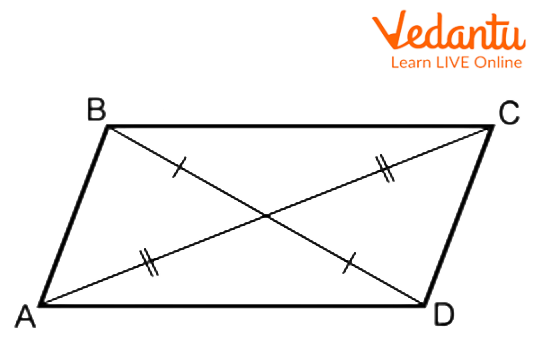
In a parallelogram, the diagonals bisect each other.
In a rhombus, diagonals are perpendicular and bisect opposite angles.
In a rectangle, diagonals are equal in length.
In a square, diagonals are equal, bisect each other, and are perpendicular.

12. What are some real-life applications of quadrilaterals?

Quadrilaterals are commonly found in real life, such as in the design of buildings, bridges, and tiles. Parallelograms are used in structures requiring stability, while trapeziums appear in the design of windows, tables, and architectural elements. Understanding quadrilaterals helps in fields like engineering, architecture, and art.

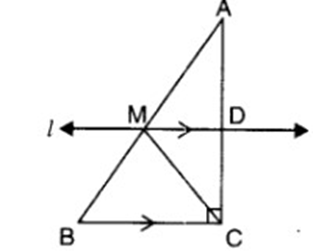
13. What is the significance of the Midpoint Theorem in quadrilaterals?

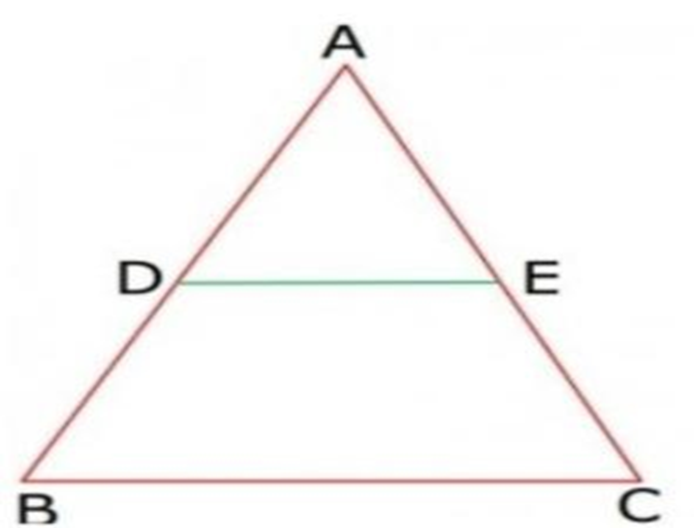
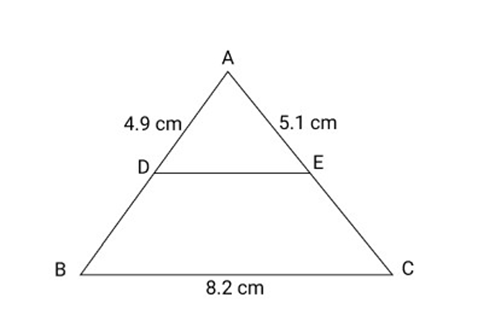
The Midpoint Theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half its length. This theorem is useful in solving problems involving quadrilaterals, as it helps in proving parallelism and calculating lengths of sides.

14. What makes the square a unique quadrilateral?

A square is unique because it possesses all the properties of a parallelogram, rectangle, and rhombus. It has equal sides, right angles, equal diagonals, and diagonals that bisect each other at right angles, making it a versatile and symmetric shape.

15. Where can I find more resources for Chapter 8 Quadrilaterals?

You can find additional resources, including important questions and solutions, on Vedantu. These resources are prepared by experts and are available for free in PDF format, making them convenient for revision and practice.

S.No	Study Materials for Class 9 Maths
1	CBSE Class 9 Maths NCERT Solutions
2	CBSE Class 9 Maths Important Questions
3	CBSE Class 9 Maths Sample Papers
4	CBSE Class 9 Maths RD Sharma Solutions
5	CBSE Class 9 Maths RS Aggarwal Solutions
6	CBSE Class 9 Maths Formulas
7	CBSE Class 9 Maths NCERT Exemplar Solutions
8	CBSE Class 9 Maths Revision Notes
9.	NCERT Class 9 Maths Book

CBSE Class 9 Maths Important Questions - Chapter 8 Quadrilaterals

Important Questions for CBSE Class 9 Maths Chapter 8 Quadrilaterals: FREE PDF Download

Access Important Questions for Class 9 Mathematics Chapter 8 - Quadrilaterals

Download Important Questions Of Chapter 8 Maths Class 9 PDF

Let’s Learn About Quadrilateral and Its Type

Definition of Quadrilateral

Types of Quadrilaterals

Important Formulas and Properties for Class 9 Maths Chapter 8 Quadrilaterals

Benefits of Class 9 Maths Chapter 8 Quadrilaterals Important Questions

Conclusion

Related Study Materials for Class 9 Maths Chapter 8 Quadrilaterals

CBSE Class 9 Maths Chapter-wise Important Questions

Related Important Links for Maths Class 9

Vedantu Tatva Pro Question Bank Book CBSE Class 9 Mathematics Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 9 Year Long Recorded Course

Vedantu Tatva Pro CBSE Class 9 book set – Physics, Chemistry, Biology.

Vedantu Tatva Pro Question Bank Book CBSE Class 9 Set of 4 Books | Mathematics , Physics, Chemistry, Biology | Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 9 Year Long Recorded Course

Vedantu's Instasolve - 1 Month - 24 hours Unlimited Instant Doubt Solving

Vedantu's Instasolve - 12 Months - 24 hours Unlimited Instant Doubt Solving

Vedantu's Instasolve - 3 Months - 24 hours Unlimited Instant Doubt Solving

Biology - Vedantu - Round Neck T-Shirt

Doctor in the House - Men's Round Neck T-Shirt

Doctor in the House - Women's Round Neck T-Shirt

Dream Hustle Achieve - Women's Round Neck T-Shirt

Dream Hustle Achieve - Men's Hooded Sweatshirt

Dream Hustle Achieve - Women's Hooded Sweatshirt

FAQs on CBSE Class 9 Maths Important Questions - Chapter 8 Quadrilaterals