




How to Calculate the Effective Focal Length of Combined Lenses in Contact
The combination of thin lenses in contact involves placing two or more lenses with negligible separation along a common optical axis. This system acts as a single lens with a new effective focal length and power, allowing for simplified analysis of image formation and optical design in advanced physics problems.
Physical Principles of Lenses in Contact
When thin lenses are placed in contact, they share a common optical axis and the distance between them is negligible compared to their focal lengths. This configuration is valid for combinations of both convex and concave lenses.
Each lens refracts light sequentially such that the image formed by one lens acts as the object for the next. The final position of the image can then be determined using a combined or effective focal length.
Analysis of the optical system utilizes the thin lens formula and superposition of the individual lens powers for accurate predictions. For a related topic, see Sign Convention In Lenses.
Formula for the Combination of Thin Lenses in Contact
For $n$ thin lenses with focal lengths $f_1, f_2, \ldots, f_n$ placed coaxially in contact, the combined or effective focal length $F$ is given by the following relation:
$\dfrac{1}{F} = \dfrac{1}{f_1} + \dfrac{1}{f_2} + \ldots + \dfrac{1}{f_n}$
Here, each focal length is taken with its proper sign: positive for a convex (converging) lens and negative for a concave (diverging) lens.
The combined optical power $P$ (in dioptres, D) of the lens system is
$P = P_1 + P_2 + \ldots + P_n$, where $P_i = \dfrac{1}{f_i}$ with $f_i$ in metres.
| Parameter | Expression |
|---|---|
| Combined focal length $F$ | $\dfrac{1}{F} = \dfrac{1}{f_1} + \dfrac{1}{f_2} + \ldots + \dfrac{1}{f_n}$ |
| Combined power $P$ | $P = P_1 + P_2 + \ldots + P_n$ |
Derivation: Combination of Thin Lenses in Contact
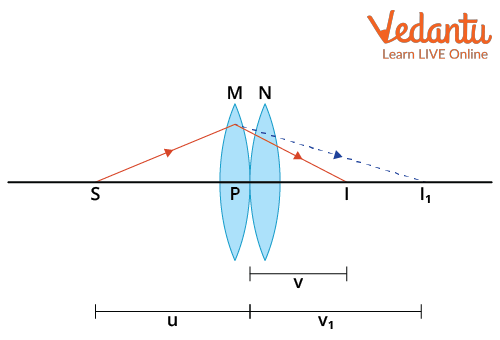
Consider two thin lenses $L_1$ and $L_2$ with focal lengths $f_1$ and $f_2$ in contact. Let an object be placed at distance $u$ from the combination. The final image forms at distance $v$ from the lenses.
First, $L_1$ forms an intermediate image at $v_1$, given by the lens formula: $\dfrac{1}{f_1} = \dfrac{1}{v_1} - \dfrac{1}{u}$.
This image acts as the object for $L_2$ such that: $\dfrac{1}{f_2} = \dfrac{1}{v} - \dfrac{1}{v_1}$.
Adding both equations: $\dfrac{1}{f_1} + \dfrac{1}{f_2} = \left(\dfrac{1}{v_1} - \dfrac{1}{u}\right) + \left(\dfrac{1}{v} - \dfrac{1}{v_1}\right) = \dfrac{1}{v} - \dfrac{1}{u}$.
By the definition of a system with equivalent focal length $F$, $\dfrac{1}{F} = \dfrac{1}{v} - \dfrac{1}{u}$. Therefore, $\dfrac{1}{F} = \dfrac{1}{f_1} + \dfrac{1}{f_2}$, which generalizes for $n$ lenses.
This derivation assumes the separation between lenses is negligible and all are placed on a common axis for accurate image alignment.
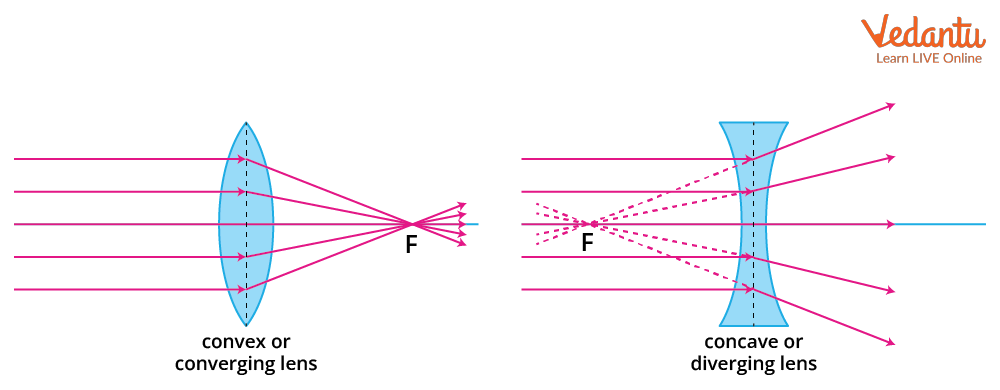
Sign Conventions for Thin Lenses in Contact
Convex (converging) lenses have positive focal length and power, while concave (diverging) lenses have negative values. All values must use the Cartesian sign convention for consistency.
In calculations, convert focal lengths to metres when determining power in dioptres. See Mirror Formula And Magnification for further understanding of optical sign convention.
Numerical Example: Combination of Two Thin Lenses in Contact
Suppose a convex lens with $f_1 = +20\ \mathrm{cm} = +0.20\ \mathrm{m}$ and a concave lens with $f_2 = -40\ \mathrm{cm} = -0.40\ \mathrm{m}$ are placed in contact. Calculate the combined focal length and power.
- $\dfrac{1}{F} = \dfrac{1}{f_1} + \dfrac{1}{f_2}$
- $\dfrac{1}{F} = \dfrac{1}{0.20} + \dfrac{1}{-0.40} = 5 - 2.5 = 2.5$
- $F = \dfrac{1}{2.5} = 0.40\ \mathrm{m}$
- $P = \dfrac{1}{0.20} + \dfrac{1}{-0.40} = 5 - 2.5 = 2.5\,\text{D}$
Therefore, the combination acts as a single converging lens with focal length $0.40$ m and power $2.5$ D.
Key Points and Common Mistakes
- Always convert focal lengths to metres when calculating power
- Use proper sign convention for lens type
- Combination formula applies only for lenses in contact
- The medium between lenses must remain the same
- Power values are always added algebraically, not multiplied
Incorrect use of sign for focal length or failure to convert units may lead to errors in calculation. The combination rule is not valid if lenses are separated by a finite distance; in that case, a more complex formula involving separation is required.
Applications of Thin Lens Combinations in Contact
The principle of combining thin lenses in contact is widely applied in designing optical instruments such as cameras, microscopes, and high-power spectacles.
Layering multiple lenses allows for precise control of focal length and system power, enabling correction of vision defects and generation of required magnification. For additional concepts, refer to Difference Between Lens And Mirror.
Skill in using these formulas is essential for JEE Main and similar exams, particularly in both calculation-based and reasoning questions. Related topics include Concave Mirror Image Formation and Thin Film Interference.
Laboratory experiments on refraction and lens combinations reinforce the practical understanding of these formulas, ensuring accurate placement and alignment of optical elements for desired results.
Questions on lens combinations also assess logical application of sequential image-object relations. Learning systematic substitution and correct use of measurement units is critical for avoiding mistakes, as discussed in Application Of Echo.
FAQs on Understanding the Combination of Thin Lenses in Contact
1. What is meant by combination of thin lenses in contact?
Combination of thin lenses in contact refers to placing two or more lenses very close together so that their combined optical effect is as a single lens. Key points include:
- The combined focal length (F) is determined by both lenses' focal lengths.
- This combination simplifies calculations for devices like microscopes and telescopes.
- The combined power is the sum of individual lens powers (P = P1 + P2 + ...).
- This concept is central in optics for analyzing complex lens systems.
2. What is the formula for the equivalent focal length of two thin lenses in contact?
The equivalent focal length of two thin lenses in contact is found using the formula:
- 1/F = 1/f1 + 1/f2, where F is the combined focal length, and f1, f2 are the focal lengths of the individual lenses.
- For more lenses: 1/F = 1/f1 + 1/f2 + 1/f3 + ...
- This relationship holds if the lenses are placed so close that distance between them is negligible.
3. What is the total power of a combination of thin lenses in contact?
The total power (P) of a combination of thin lenses in contact is the sum of their individual powers:
- P = P1 + P2 + ... + Pn, where P1, P2 are the powers of each lens.
- Power is measured in dioptres (D) and defined as P = 1/f (in meters).
- This is a key concept in CBSE optics and important for lens problem-solving.
4. Why are combinations of thin lenses in contact used in optical instruments?
Combinations of thin lenses in contact are used to achieve desired optical effects that a single lens cannot provide:
- To increase or decrease overall focal length.
- To correct chromatic or spherical aberrations.
- For functions like magnification in telescopes and microscopes.
- This allows fine-tuning of image formation properties.
5. What is the difference between adding lens powers and focal lengths in thin lens combinations?
In thin lens combinations in contact:
- Powers add algebraically: P = P1 + P2
- Focal lengths combine reciprocally: 1/F = 1/f1 + 1/f2
- This reflects the mathematical difference between combining power and focal length.
6. Can the combination of two convex lenses result in a divergent (negative focal length) system?
A combination of two convex (converging) lenses normally produces a converging (positive) system:
- If a convex lens is combined with a concave (diverging) lens, the result could be converging or diverging depending on the values of their focal lengths.
- To get a net negative focal length, the diverging effect must outweigh the converging effect.
7. What happens to the focal length if more lenses are combined in contact?
When more thin lenses are placed in contact, the combined focal length generally decreases if all are positive or increases in magnitude if negative:
- 1/F = 1/f1 + 1/f2 + 1/f3 + ...
- Each additional lens influences the net optical power, changing the final focal length.
8. What is the equivalent power of a combination of a convex lens of focal length +20 cm and a concave lens of focal length -30 cm in contact?
To find the equivalent power (P):
- P1 = 1/f1 = 1/0.20 = +5 D (for convex lens)
- P2 = 1/f2 = 1/(-0.30) = -3.33 D (for concave lens)
- Total power, P = +5 D + (-3.33 D) = +1.67 D
- So, the combination acts as a weak converging lens.
9. What is the effect of placing a glass slab between two thin lenses in contact?
Placing a glass slab between two thin lenses effectively separates them, and their combination formula must be modified:
- The simple formula (1/F = 1/f1 + 1/f2) is valid only when lenses are in contact.
- With a glass slab, one must use the general lens-maker's formula considering separation and medium's refractive index.
- This can alter the focal length and effective power.
10. If the powers of two lenses in contact are +4D and -2D, what is the focal length of the combination?
The combined power (P) is the sum of powers:
- P = +4D + (-2D) = +2D
- Focal length, F = 1/P = 1/2 = 0.5 m or 50 cm
- This combination acts as a weak converging lens.
11. State the conditions under which two thin lenses can be considered ‘in contact’.
Two thin lenses are considered ‘in contact’ when:
- The distance between them is negligible compared to their focal lengths.
- No significant medium (like air gap or glass slab) separates them.
- They are mounted so their principal axes are perfectly aligned.
This allows their combined focal length to be calculated directly using the contact formula.
























