




Key Differences Between Convex and Concave Lenses with Examples
Convex and concave lenses are essential optical elements used to control the direction and convergence of light rays. Their differing shapes produce distinct effects on incident light, playing a crucial role in image formation and vision correction. A clear understanding of their properties, behavior, and applications is fundamental in optics and JEE Main Physics.
Structure and Properties of Convex and Concave Lenses
A convex lens is thicker at the center and thinner at the edges. It converges parallel rays of light towards a single point known as the principal focus. In contrast, a concave lens is thinner at the center and thicker at the edges, causing parallel rays to diverge as if they emanate from the principal focus on the same side as the source.
Convex lenses are termed converging lenses due to their ability to bring light rays together. Concave lenses are called diverging lenses because they spread light rays apart. The sign convention assigns a positive focal length to convex lenses and a negative focal length to concave lenses. These sign rules are explained in detail under the Sign Convention Of Lens And Mirror topic.
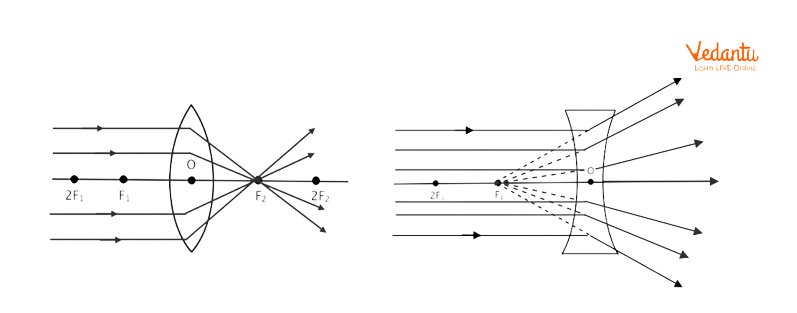
Difference Between Convex and Concave Lenses
Convex and concave lenses differ in shape, light ray behavior, image formation, and focal length sign. Key differences are summarized in the following table.
| Convex Lens | Concave Lens |
|---|---|
| Thicker at center, converging | Thinner at center, diverging |
| Positive focal length (+f) | Negative focal length (−f) |
| Can form real or virtual images | Forms only virtual images |
| Used in magnifiers, cameras | Used in glasses for myopia |
Types of Convex and Concave Lenses
Convex lenses include biconvex, plano-convex, and concavo-convex types. Biconvex lenses have both surfaces outwardly curved, plano-convex lenses have one flat and one convex surface, while concavo-convex have one surface convex and the other concave but with more pronounced convexity.
Concave lenses include biconcave, plano-concave, and convexo-concave forms. Biconcave lenses are inwardly curved on both surfaces, plano-concave have one flat and one concave surface, and convexo-concave (or meniscus) have a convex and a more strongly curved concave surface. The physical structure determines their light ray manipulation.
Ray Diagrams and Image Formation
Ray diagrams describe the image formation process for both lens types. A convex lens focuses parallel incident rays to a real point on the opposite side of the lens, forming real or virtual images depending on object position. A concave lens diverges parallel rays, making them appear to originate from a virtual focus on the same side as the source.
The main rules for ray tracing in lenses are: a ray parallel to the principal axis passes through (or appears to diverge from) the focal point; a ray through the optical center passes undeviated; a ray through the principal focus emerges parallel to the axis. Proper use of these facilitates precise determination of image position and nature.
The conventions applied in these diagrams follow the Cartesian sign system. Details regarding lens and mirror conventions are provided in the Difference Between Mirror And Lens guide.
Lens Formula and Magnification
Both convex and concave lenses obey the thin lens formula expressed as:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where $f$ is focal length, $v$ is image distance, and $u$ is object distance (all measured from the optical center).
Magnification ($m$) is given by:
$m = \dfrac{v}{u} = \dfrac{h'}{h}$
where $h'$ is image height and $h$ is object height. For convex lenses, $f$ is positive; for concave lenses, $f$ is negative. Careful use of sign conventions is crucial when applying these relationships to numericals.
For extended calculations involving multiple thin lenses, power addition and the use of advanced formulas are explained in the context of optical systems.
Solved Example: Calculating Image Formed by a Convex Lens
Consider an object of height $2.0\,\text{cm}$ placed $12\,\text{cm}$ from a convex lens of focal length $6\,\text{cm}$. To find the image distance $v$:
Given: $u = -12\,\text{cm}$, $f = +6\,\text{cm}$
$\dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u} = \dfrac{1}{6} + \dfrac{1}{-12} = \dfrac{1}{12}$
$v = +12\,\text{cm}$ (real, inverted image forms on the other side)
Magnification: $m = \dfrac{v}{u} = \dfrac{12}{-12} = -1$ (Image is real, inverted, and same size as object)
Further examples can be constructed for concave lenses using similar methodology, noting the sign change for the focal length.
Applications of Convex and Concave Lenses
Convex lenses find application in microscopes, telescopes, magnifiers, projectors, and are integral to the functioning of the human eye. Further reading is available in the Real Depth And Apparent Depth article for related optical phenomena.
Concave lenses are utilized in correcting myopia (short-sightedness), peepholes in doors, and certain optical instruments for spreading out beams and correcting aberrations.
Common Mistakes and Precautions in Lens Problems
Frequent errors include incorrect assignment of sign conventions, improper ray tracing, and confusion between rules for mirrors and lenses. Strictly adhere to the Cartesian sign system and specific ray tracing rules for accuracy in numerical and diagrammatic solutions. For sign conventions in depth, refer to the Mirror Formula And Magnification explanation.
- Convex lens: Positive focal length, real or virtual image possible
- Concave lens: Negative focal length, only virtual images form
- Use appropriate ray tracing rules
- Apply SI units consistently in calculations
FAQs on Understanding Convex and Concave Lenses for Students
1. What is the difference between convex and concave lenses?
Convex and concave lenses differ in shape, image formation, and light ray behavior.
- Convex lens is thicker at the center and converges light rays (called a converging lens).
- Concave lens is thinner at the center and diverges light rays (known as a diverging lens).
- Convex lenses can form real or virtual images, while concave lenses only form virtual images.
2. What are the uses of convex and concave lenses?
Convex and concave lenses are widely used in daily life and scientific devices.
- Convex lenses are used in magnifying glasses, cameras, eye glasses for hypermetropia, and in microscopes.
- Concave lenses are used in spectacles for myopia (short-sightedness), peepholes, and some telescopes.
3. What type of image is formed by a convex lens?
Convex lens can produce both real and virtual images depending on object placement.
- Placing the object beyond the focal point forms a real, inverted image.
- Placing the object between the lens and its focus forms a virtual, erect, and magnified image.
4. Where is the concave lens placed for correction of myopia?
Concave lenses are used in spectacles for persons with myopia (short-sightedness).
- A concave lens diverges light rays before entering the eye, helping focus images correctly on the retina.
5. How do you distinguish between a convex and concave lens by touching?
Convex lenses feel thicker at the center and thinner at the edges, while concave lenses are thinner at the center and thicker at the edges.
- Run your finger along the lens surface:
- Convex lens: Bulges outward at the center
- Concave lens: Curves inward at the center
6. What is the principal focus of a lens?
Principal focus is the point where parallel incident rays either converge (convex) or appear to diverge (concave) after refraction through the lens.
- For convex lens: Real focus where rays converge.
- For concave lens: Virtual focus from which rays appear to diverge.
7. What are the rules for image formation by convex lenses?
Image formation by convex lenses follows basic ray rules.
- A ray parallel to the principal axis passes through the focus after refraction.
- A ray passing through the optical center goes straight without deviation.
- A ray passing through the focus emerges parallel to the axis.
8. Can a concave lens form a real image?
Concave lens usually forms only virtual, erect, and diminished images.
- A concave lens cannot form a real image for real objects because diverged rays do not meet in real space.
9. What happens when parallel rays pass through a convex lens?
When parallel rays pass through a convex lens, they converge at the principal focus.
- This is known as the converging action of a convex lens.
10. State one difference between real and virtual images formed by lenses.
Real images can be obtained on a screen, while virtual images cannot be projected.
- Real image: Formed by actual intersection of rays; inverted.
- Virtual image: Formed by apparent intersection; erect and cannot be captured on a screen.
11. What do you mean by power of a lens?
Power of a lens indicates its ability to bend light, and is the reciprocal of its focal length (in meters).
- Measured in Dioptres (D).
- P = 1/f where f is the focal length in meters.
























