JEE Main Physics 2025: Magnetic Field Due to Straight Wire Carrying Current

The magnetic field produced by a straight current-carrying wire is a fundamental concept in electromagnetism, essential for understanding how electrical currents generate magnetic forces. When an electric current flows through a conductor, it creates a magnetic field around the wire. This field is circular, and its strength depends on the current and the distance from the wire.

In this section, we will explore the formula for the magnetic field due to a straight wire, the derivation of this formula, and its significance in various real-world applications, such as electromagnets and electric motors. Understanding this concept is crucial for students preparing for competitive exams like JEE Main. Let’s dive deeper into the principles and calculations behind the magnetic field of a straight current-carrying wire.

What is Magnetic Field Due to Straight Wire Carrying Current?

The magnetic field due to a straight wire carrying current refers to Magnetic fields that are produced when current passes through a wire or a loop. Moreover, a strong current is required to produce a strong magnetic field. A long straight wire carrying current will produce a magnetic field. If we place another current-carrying wire in its vicinity, it experiences a force that is produced by the first current-carrying wire. 

We derive this force on the wire using Biot's Savart's Law. Biot Savart’s law states the relationship between a current-carrying wire and a point P placed at a distance r from the wire. The magnitude of this magnetic field is inversely proportional to the square of the distance of wire to the point P kept at distance r. 

Magnetic Field Due to Straight Current Carrying Wire Formula

The magnetic field due to straight wire is produced by moving charges. The direction of this current can be found out from Maxwell's right thumb rule. 

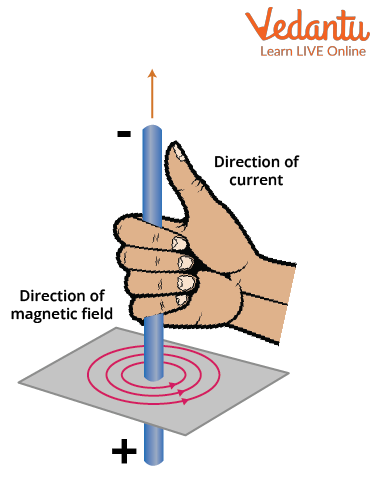
Right Hand thumb Rule

Right Hand Thumb Rule: The right hand thumb rule states that when we curl our fingers in the direction of the magnetic field, the direction of the thumb gives the direction of the current. Inversely, it can also be stated that if the thumb represents the direction of current, then the fingers denote the direction of the magnetic field. 

Assuming a long straight current carrying a wire of magnitude I, the magnetic field (B) created by the conductor is formed around it. The magnetic field also further depends on the distance of the wire. Thus, the magnetic field created by the current-carrying wire is denoted as the ratio of the product of magnetic permeability and current to its distance from the wire. Mathematically, it can be denoted as : 

$B=\dfrac{\mu{ }_{o}I}{2 \pi r}$ 

where

$\mu$ is the permeability of free space or $4\pi\times10^{-7}~\left(\dfrac{T\cdot m}{A}\right)$.

B is the magnetic field measure in tesla.

I is the current intensity flowing in the long wire.

r is the distance of the magnetic field from the wire. 

Magnetic Field Due to Straight Current Carrying Wire Derivation

Suppose we assume a point P at a distance r from a long straight wire carrying current I. 

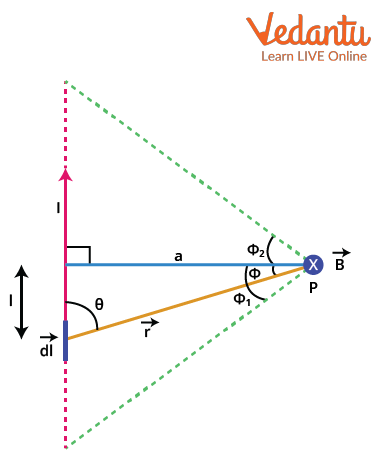
Magnetic Field due to Long Straight Wire

Now, according to Biot Savart’s Law, the magnetic field of a point P placed at a distance r is

$ \mathrm{d} B=\dfrac{\mu_{\theta} I d l \sin (\theta)}{4 \pi r^{2}}$

From the figure, it can be seen that

$\begin{align} &r=\sqrt{a^{2}+l^{2}} \\ &\sin \theta=\dfrac{r}{\sqrt{a^{2}+l^{2}}} \end{align}$

We need to calculate the magnetic field for the entire conductor. We can find this by integrating the equation for half the wire and multiplying it by 2. Then, the limits of the integral will be from 0 to infinity. 

The integration gives

$\int d B=2 \times \int_{0}^{\infty} \dfrac{\mu_{0} I}{4 \pi} \dfrac{1}{\left(\sqrt{r^{2}+l^{2}}\right)^{2}} \dfrac{r}{\sqrt{r^{2}+l^{2}}} \mathrm{~d} l$

$B=\dfrac{\mu_{0} I}{2 \pi} \int_{0}^{\infty} \dfrac{r}{\left(r^{2}+l^{2}\right)^{3 / 2}} \mathrm{~d} l$

$B=\dfrac{\mu_{0} I}{2 \pi r}\left[\dfrac{l}{\left(r^{2}+l^{2}\right)^{1 / 2}}\right]_{0}^{\infty}$

$\begin{align} &B=\dfrac{\mu_{0} I}{2 \pi r}\left[\lim _{l \rightarrow \infty}\dfrac{l}{l\left(\dfrac{r^{2}}{l^{2}}+1\right)^{\dfrac{1}{ 2}}}-0\right] \\ &B=\dfrac{\mu_{0} I}{2 \pi r}\left[\dfrac{1}{\left(\dfrac{r^{2}}{\infty}+1\right)^{\dfrac{1}{ 2}}}-0\right] \\ &B=\dfrac{\mu_{0} I}{2 \pi r}[1-0] \\ &B=\dfrac{\mu_{o} I}{2 \pi r}\end{align}$

Thus, the magnetic field due to a long straight current carrying wire is inversely proportional to the distance of a point P from the wire. 

Electric Field Due to Straight Wire

The electric field for a long straight current-carrying wire is denoted as: $E=\dfrac{\lambda}{2 \pi \in{ }_{o}{r}}$

where r is the distance of the electric field from the wire, $\lambda$ is the linear charge density, and $\in_{o}$ is the permittivity whose value is 8.854 $\times$ 10^-12 .

This field can be calculated by considering an infinitely long straight wire and then using a cylindrical gaussian surface. The gauss law can then be used to find the electric field of this straight wire. 

Solved Examples on Magnetic Field Due to Long Straight Wire

Example 1:  A wire of 60 cm in length carries a current I= 4 A. What is the magnetic field at 50 cm from the wire?

Solution: 

As derived from above the formula, magnetic field of a straight line is denoted as: 

$B=\dfrac{\mu I}{2 \pi r}=\dfrac{4 \pi \times 10^{-7} .4}{(2 \pi \times 0.6 m)}=13.33 \times 10^{-7}$

Thus, the value of the magnetic field comes out to be 13.33 $\times$ 10-7 tesla.

Example 2: A wire of 60 cm in length carries a current I= 3 A. At which distance is the magnetic field 2 $\times$ 10^-3 T?

Solution:

As derived from above the formula, magnetic field of a straight line is denoted as: 

$\begin{align}&r=\dfrac{\mu I}{2 \pi B}=\dfrac{4 \pi \times 10^{-7} \times 3}{2 \pi \times 2 \times 10^{-3}} \\ &r=0.6 \times 10^{-4} \mathrm{~m}=0.06 \mathrm{~mm} \end{align}$

Thus, the distance at which the magnetic field is 2 $\times$ 10^-3 T is 0.06 mm. 

Example 3: Find the electric field at 6m from an infinitely long wire with a linear charge density of 8 x 10^-3 $\dfrac{C}{m}$. 

Solution:

Given r = 5m and $\lambda$=   8 $\times$ 10^-3 cm. Substituting these in the above formula, we get, 

$\begin{align}E=\dfrac{\lambda}{2 \pi \in{ }_{o}^{r}} \\E=\dfrac{8 \times 10^{-3}}{2 \pi \times 6 \times 8.854 \times 10^{-12}}\\ E=0.047 \times 10^{9}\,N/C \\ \end{align}$

Hence, the value of electric field is $0.047 \times 10^{9}\,N/C$.

Example 4:  A straight current-carrying conductor is carrying a current of  10A and another conductor parallel to it carries a current of 15A on the opposite side as shown in the figure below. Find the magnitude of the magnetic field produced by the system at a distance of 2 m. 

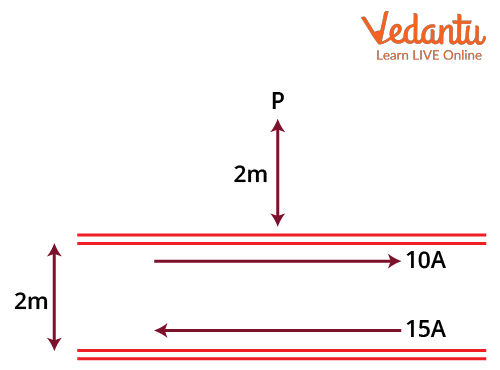
Diagram for the problem

Solution:  The problem has two wires. Now we can find the magnetic field by individual wires and then add them to get the total magnetic field. Let the magnetic field by wire carrying 10A current be B₁. We can write B₁ as

$\begin{align} &B_{1}=\dfrac{\mu_{o}{I}_1}{2 \pi r_{1}} \\ &B_{1}=\dfrac{2 \mu_{o} \times 10}{4 \pi \times 2} \\ &B_{1}=10^{-7} \times 10 \\ &B_{1}=10^{-6} \mathrm{~T} \end{align}$

Similarly, the magnetic force B2 by second wire carrying current 15 A and at distance 4m from P can be given as

$\begin{align} &B_{2}=\dfrac{\mu_{0} I_{2}}{2 \pi r_{2}} \\ &B_{2}=\dfrac{2 \mu_{0} \times 15}{4 \pi \times 4} \\ &B_{2}=10^{-7} \times \dfrac{15}{2} \\ &B_{2}=0.75 \times 10^{-6} \mathrm{~T} \end{align}$

Now, both the wires have opposite directions, so the total magnetic field will be given by the difference of their individual magnetic fields. Thus, the total  magnetic field B at point P can be written as

$\begin{align} &B=B_{1}-B_{2} \\ &B=10^{-6}-0.75 \times 10^{-6} \\ &B=0.25 \times 10^{-6} \mathrm{~T} \end{align}$ 

So, the magnetic field by both wires at point P is 0.25$\times$ 10^-6 T.

Key Points on Magnetic Field Due To Straight Wire Carrying Current

• Direction of the magnetic field: The direction of the magnetic field around the wire is given by the right-hand thumb rule. If you point the thumb of your right hand in the direction of the current, your curled fingers will show the direction of the magnetic field.

• Magnetic field strength: The strength of the magnetic field BBB at a distance rrr from a straight, long, current-carrying wire is directly proportional to the current III and inversely proportional to the distance rrr from the wire. The formula is:
  $B = \dfrac{\mu_0 I}{2 \pi r}$
  Where:

• B is the magnetic field strength,

• $\mu_0$​ is the permeability of free space ($4\pi \times 10^{-7} \, \text{T m/A}$),

• I is the current,

• r is the distance from the wire.

Characteristics on Magnetic Field Due to Straight Wire Carrying Current

• The magnetic field forms concentric circles around the wire.

• The strength of the magnetic field decreases as the distance from the wire increases.

• The magnetic field is strongest near the wire and weakens with distance.

Applications on Magnetic Field Due to Long Straight Wire

The magnetic field due to a long straight wire carrying current has several practical applications in the fields of electronics, engineering, and physics. Here are some important applications:

1. Electromagnetic Induction (Motors and Generators): The magnetic field generated by a current-carrying wire is used in the operation of motors and generators. In motors, a magnetic field interacts with the current in a coil to produce motion (Lorentz force). The same principle is used in electromagnetic induction to generate electricity.

2. Magnetic Field in Electric Circuits: The magnetic field around a current-carrying wire is crucial in designing circuits that rely on the interaction of current and magnetic fields. Devices like inductors and transformers use the magnetic field to control electrical energy flow, either by storing energy or by transferring energy between circuits.

3. Electromagnets: The magnetic field generated by a straight current-carrying wire is the basis for creating electromagnets. By wrapping a wire around a ferromagnetic core, a strong magnetic field is created, which is useful in applications like magnetic cranes, MRI machines, and electric bells.

4. Magnetic Shielding: The understanding of the magnetic field due to a straight wire is used in magnetic shielding. In this application, a conductor is placed around sensitive equipment (like electronic devices) to shield them from external magnetic fields. By knowing how the magnetic field behaves around a current-carrying wire, engineers can design shields that reduce the effects of unwanted magnetic interference.

Conclusion

The article presents a thorough walkthrough of the magnetic field for a long infinite straight current carrying wire. The magnetic field is created due to current and its strength depends on the magnitude of the current. The magnetic field for a long straight infinite current carrying wire is inversely proportional to its distance from the wire. Electric field on the other hand  is denoted as $E=\dfrac{\lambda}{2 \pi \in{ }_{o}{r}}$, which is again inversely proportional to the distance of the point from the wire.

JEE Main 2025 Subject-Wise Important Chapters

The JEE Main 2025 subject-wise important chapters provide a focused strategy for Chemistry, Physics, and Maths. These chapters help students prioritise their preparation, ensuring they cover high-weightage topics for better performance in the exam.

Check Other Important Links for JEE Main 2025 

JEE 2025 needs well-structured study materials. Here are some valuable resources to help you plan your preparation and practice efficiently.