




How Do Different Types of Manometers Work?
A manometer is a precise instrument used to measure the pressure of fluids by utilizing columns of liquid in a bent tube. It plays a vital role in fluid mechanics and is commonly employed in laboratories, industries, and calibration procedures for other pressure-measuring devices.
Definition and Principle of Manometer
A manometer operates on the principle of balancing the fluid pressure with a known column of liquid, such as mercury or water. The difference in liquid height directly correlates to the pressure being measured, making manometers reliable for both absolute and gauge pressure determination.
Types of Manometer
Manometers can be classified based on their construction and the type of pressure measurement they perform. The two main categories are simple manometers and differential manometers. Each category includes specific forms suitable for various measurement needs.
- Simple manometer
- Differential manometer
- Piezometer
- U-tube manometer
- Single column manometer
- Inclined manometer
- Inverted U-tube manometer
Piezometer
The piezometer is the simplest type of manometer. It consists of a vertical tube with one end connected to the fluid whose pressure is to be measured and the other end open to the atmosphere. The pressure is determined by the height to which the liquid column rises in the tube.
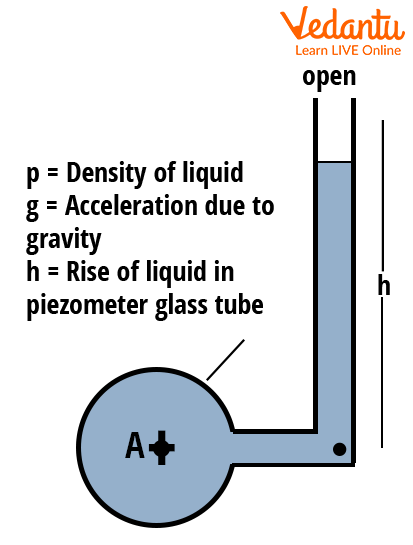
The pressure at the measurement point is given by $P = \rho g h$, where $\rho$ is the liquid density, $g$ is the acceleration due to gravity, and $h$ is the height of the liquid column.
U-Tube Manometer
The U-tube manometer consists of a glass tube bent into a U-shape. One end is exposed to the fluid under investigation, and the other end is typically open to the atmosphere. This type enables accurate measurement of gauge pressure.
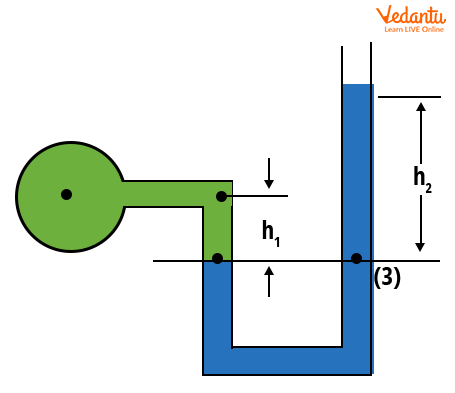
The gauge pressure is calculated using the formula $p = \rho_2 g h_2 - \rho_1 g h_1$, where $\rho_1$ and $\rho_2$ are the densities of the two liquids, and $h_1$, $h_2$ are their respective heights above the reference line.
For related pressure concepts, refer to Absolute Pressure Formula.
Single Column Manometer
A single column manometer is a modified U-tube manometer, where one limb is replaced with a reservoir of large cross-sectional area. This design increases sensitivity to small pressure differences.
Single column manometers are further classified as vertical and inclined types based on the orientation of the measuring limb.
Vertical Single Column Manometer
In a vertical single column manometer, one limb is a large reservoir, and the other is a slim vertical tube. The pressure is determined by the height change in the vertical tube relative to the reference line.
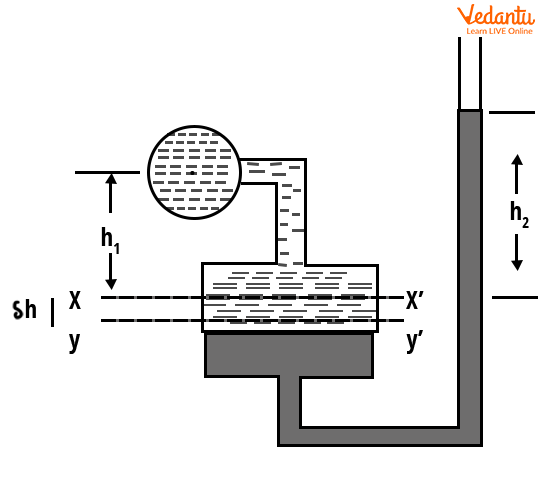
The pressure at the reference is calculated as $P = \rho_{2} g h_{2} - \rho_{1} g h_{1}$.
Inclined Single Column Manometer
The inclined single column manometer enhances sensitivity by inclining the measuring limb, which provides a greater length for the same vertical rise. This permits finer pressure measurements.
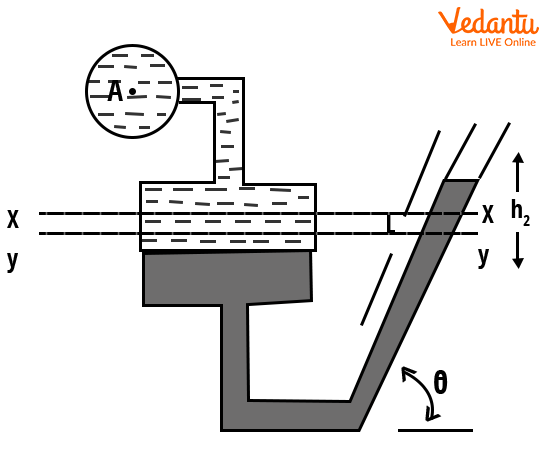
The pressure difference is given by $P = \rho_{2} g h_{2} \sin\theta - \rho_{1} g h_{1}$, where $\theta$ is the inclination angle of the tube.
Differential Manometers
Differential manometers are designed to measure the pressure difference between two points within a fluid system. These are widely used for applications such as pipe flow and laboratory experiments.
Types include the U-tube differential manometer and the inverted U-tube manometer. Each type offers specific advantages depending on the required application.
U-Tube Differential Manometer
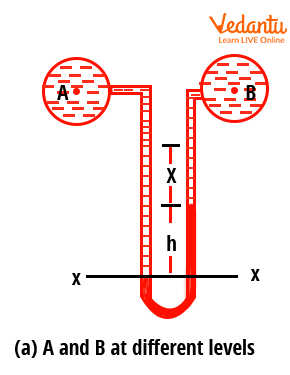
A U-tube differential manometer connects two different points in a fluid system. It measures the pressure difference directly as the difference in liquid column heights in the two limbs.

If $P_A$ and $P_B$ are the pressures at points A and B, and $h$ is the difference in height of the high-density liquid, then:
$P_A - P_B = h g (\rho_g - \rho_1) + \rho_2 g y - \rho_1 g x$.
This equation applies when points A and B are at different levels.
Inverted U-Tube Differential Manometer
The inverted U-tube differential manometer is used to measure small differences in pressure between two points containing the same liquid with a lighter manometric fluid. The tube is inverted to trap low-density liquid between the points.
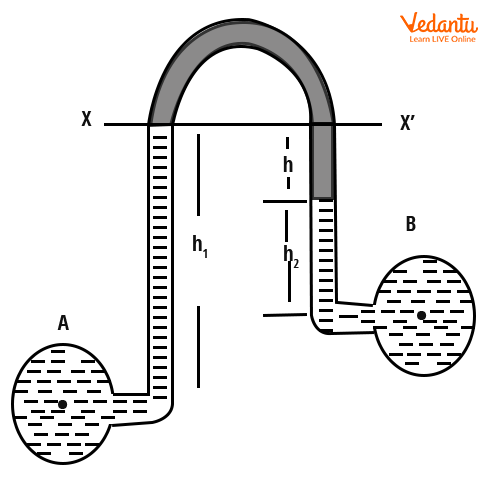
The formula for pressure difference is $P_A - P_B = h_1 g \rho_1 - \rho_2 g h_2 - \rho_l g h$, where $\rho_1$, $\rho_2$, and $\rho_l$ denote the densities of the corresponding sections.
Comparison: Manometer vs Barometer
While a manometer measures the pressure of a fluid relative to the atmospheric pressure, a barometer measures atmospheric pressure exclusively. The principle of operation is similar but the application differs in the type of pressure determined.
| Parameter | Manometer |
|---|---|
| Measures fluid pressure | Yes |
| Measures atmospheric pressure | No |
| Types of liquid used | Mercury, Water |
| Application | Fluid systems, calibration |
Applications of Manometer
Manometers are extensively used in fluid mechanics laboratories, industrial process control, calibration of pressure instruments, and studies involving the mechanics of liquids and gases.
- Measurement of pressure in pipe flows
- Calibration of gauges and sensors
- Fluid mechanics laboratory experiments
- Verification of pressure drop in engineering systems
For further review of related concepts, visit Properties Of Solids.
Summary of Manometer Types
Manometers are essential instruments in pressure measurement due to their simplicity and accuracy. Each type, such as piezometer, U-tube, single column, and differential manometer, serves specific functions and measurement ranges as required in practice.
A thorough understanding of manometer operation and applications is beneficial for fluid mechanics and relevant engineering examinations. Related analytical approaches can be further explored in Circuit Solving.
FAQs on What Is a Manometer and Its Different Types?
1. What is a manometer?
A manometer is an instrument used to measure the pressure of gases or liquids.
Key facts:
- Manometers work by comparing the pressure of a fluid to atmospheric pressure or another reference point.
- They are essential in physics and engineering for accurate pressure measurements.
- Common fluids used inside manometers include mercury and water.
2. What are the types of manometers?
There are several main types of manometers used for different applications:
- Simple manometer: Has an open or closed tube, like the U-tube manometer.
- Differential manometer: Measures the difference between two pressures, often between two points in a system.
- Digital manometer: Uses electronic sensors to display the pressure reading digitally.
- Other types include inclined manometers and micromanometers for low-pressure applications.
3. How does a manometer work?
A manometer works by balancing the weight of a fluid column between two pressure sources.
- The difference in height of the fluid columns indicates the pressure difference.
- For a U-tube manometer, one end is connected to the system and the other to the atmosphere or another pressure source.
- The height difference, combined with the density of the fluid, determines the unknown pressure using the formula: P = hρg.
4. What is a U-tube manometer?
A U-tube manometer is a simple device consisting of a U-shaped glass tube partially filled with liquid.
Features and uses:
- One limb connects to the source of pressure; the other limb may be open or closed.
- Measures gauge pressure or differential pressure.
- The difference in fluid level between the two arms shows the measured pressure.
5. What is the difference between an open and closed manometer?
Open and closed manometers differ in how they reference pressure:
- Open manometer: One end is open to the atmosphere, used to measure gauge pressure.
- Closed manometer: One end is sealed (vacuum), used to measure absolute pressure.
6. What are the advantages and disadvantages of a manometer?
Manometers offer high accuracy but have some limitations.
Advantages:
- Simple design and operation
- High accuracy for low pressures
- No calibration required for basic types
- Not suitable for very high pressures
- Fragile and bulky
- Mercury used can be hazardous
7. What are digital manometers and how do they differ from traditional manometers?
Digital manometers use electronic sensors to measure pressure and display the reading digitally.
- They offer faster, easier, and more precise readings than traditional devices.
- Can store data and measure a wider range of pressures.
- Often preferred in modern industrial and laboratory settings.
8. What is the working principle of a differential manometer?
A differential manometer works by connecting both limbs to two different points whose pressure difference is to be measured.
- The height difference in the liquid column represents the exact pressure difference between the two points.
- Commonly used for measuring pressure drops across pipes, valves, or filters.
9. What is the formula for calculating pressure using a manometer?
The standard manometer formula is:
P = hρg
- P: Pressure difference
- h: Height difference between fluid columns (in metres or cm)
- ρ: Density of manometer liquid (e.g., water or mercury)
- g: Acceleration due to gravity (9.8 m/s²)
10. Where are manometers used in real life?
Manometers have many real-life applications.
- Checking gas pressure in laboratories and industries
- Testing ventilation and air-conditioning systems
- Calibrating and testing other pressure instruments
- Used in weather instruments and fluid mechanics experiments
11. What is the difference between manometer and barometer?
The difference between manometer and barometer lies in their usage and reference point.
- Manometer: Measures pressure of enclosed fluids relative to atmospheric or another reference pressure.
- Barometer: Specifically measures atmospheric pressure only.
























