




Equations and Factors Affecting Charged Particle Motion in Electric Fields
The motion of a charged particle in an electric field is a fundamental concept in electrostatics, essential for understanding how charges behave under the influence of electric forces. This topic is critical for JEE Main Physics, as it links the effects of electric fields to particle dynamics, force, acceleration, and resulting trajectories.
Definition and Properties of Electric Field
An electric field is a region around a charged object where other charges experience a force. The electric field direction depends on the sign of the source charge, with field lines directed outward from positive charges and inward towards negative charges.
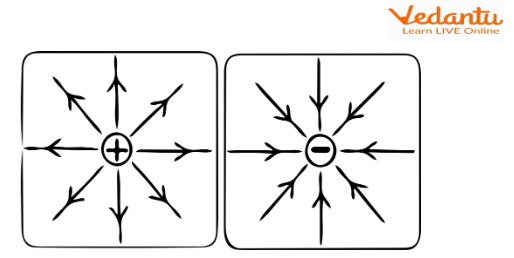
Electric field lines indicate both the strength and the direction of the field at different points in space. The density of lines corresponds to the field intensity, which can be mathematically expressed using Coulomb's law.
Electric Field Due to a Point Charge
The magnitude of the electric field $\vec{E}$ at a distance $r$ from a point charge $q_0$ is derived from the electrostatic force between two point charges. The force experienced by a test charge $q$ in the field of $q_0$ is given by:
$\left| F \right| = k \dfrac{q_0 q}{r^2}$, where $k = \dfrac{1}{4\pi \varepsilon_0}$.
The electric field at a point is then defined as the force per unit charge:
$\vec{E}(r) = \dfrac{\vec{F}(r)}{q} = k \dfrac{q_0}{r^2}$, directed radially outward for positive charges and inward for negative charges.
For more details on the structure and properties of field lines, refer to Electric Field Lines And Its Properties.
Force on a Charged Particle in an Electric Field
A charged particle of charge $q$ placed in an electric field $\vec{E}$ experiences a force given by $\vec{F} = q\vec{E}$. The direction of the force is parallel to $\vec{E}$ for a positive charge and antiparallel for a negative charge.
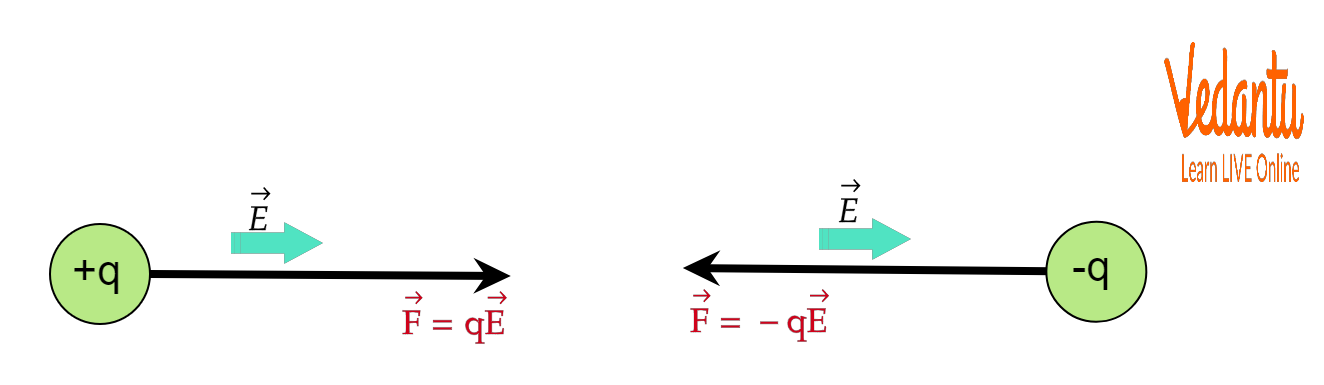
This electric force causes the particle to accelerate according to Newton's second law. If only the electric field acts on the charge, then $m\vec{a} = q\vec{E}$, so acceleration $\vec{a} = \dfrac{q\vec{E}}{m}$, which is constant in a uniform field.
Equations of Motion for a Charged Particle in a Uniform Electric Field
If a particle of mass $m$ and charge $q$ enters a region of uniform electric field $\vec{E}$, the equations of motion are determined by the constant acceleration due to the electric force.
For initial velocity $u$ and acceleration $a = \dfrac{qE}{m}$, the velocity and displacement after time $t$ are:
$v = u + at$
$s = ut + \dfrac{1}{2} a t^2$
If the particle starts from rest, $u=0$, so:
$v = \dfrac{qE}{m}t$
$s = \dfrac{1}{2} \left(\dfrac{qE}{m}\right)t^2$
Trajectory of a Charged Particle in a Uniform Electric Field
If a charged particle enters a uniform electric field with an initial velocity perpendicular to the field direction, its motion is analogous to projectile motion. The field applies a constant acceleration perpendicular to the initial velocity.
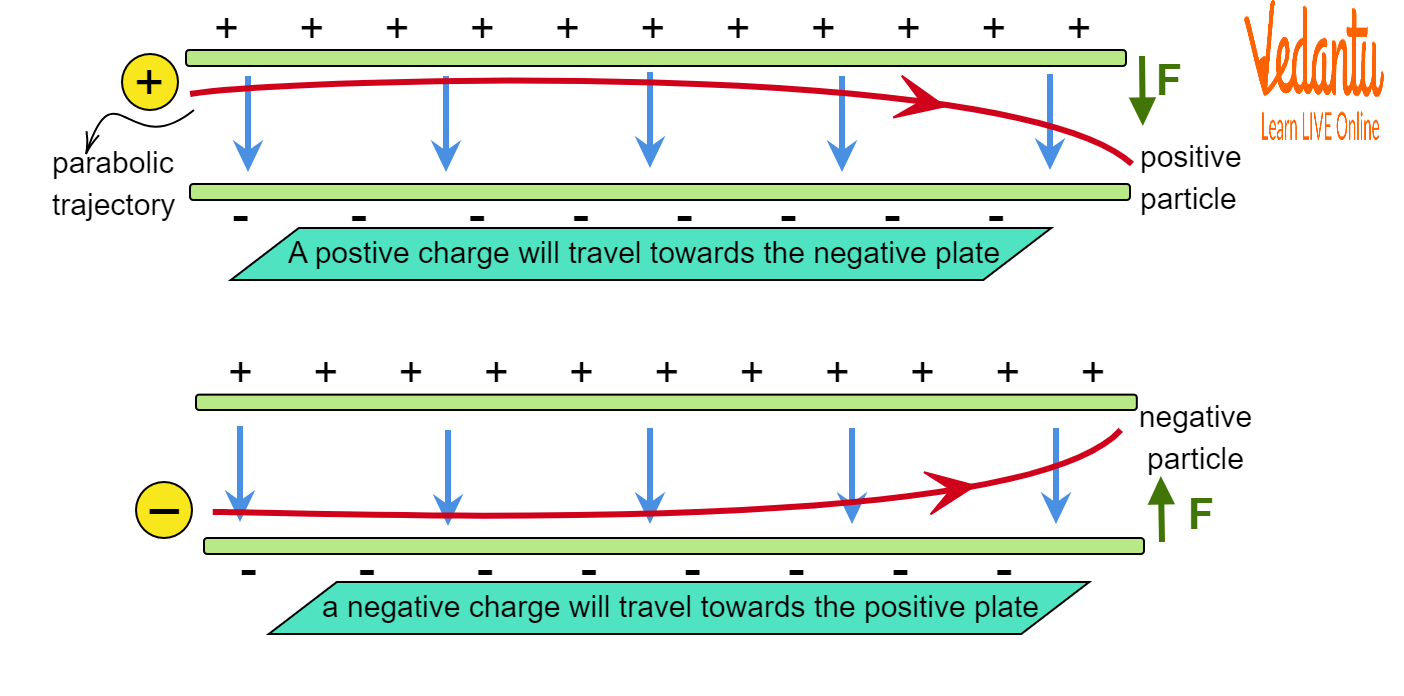
Let the electric field be along the $y$-axis and the particle enter with velocity $u_x$ along the $x$-axis. The motion in $y$ direction is governed by $a = \dfrac{qE}{m}$. The position as a function of time:
$x = u_x t$
$y = \dfrac{1}{2} \left(\dfrac{qE}{m}\right)t^2$
Eliminating $t$, $t = \dfrac{x}{u_x}$ gives the equation of the trajectory:
$y = \dfrac{1}{2} \left(\dfrac{qE}{m}\right)\left(\dfrac{x}{u_x}\right)^2$
This equation describes a parabola, indicating that the trajectory of a charged particle in a uniform electric field is parabolic.
Direction of Motion Based on Charge Sign
A positively charged particle accelerates in the direction of the electric field, while a negatively charged particle accelerates in the opposite direction. This influences the nature of displacement and the direction of the resulting parabolic path.
For further comparison with magnetic fields, review Charge In A Magnetic Field.
Key Formulas for Motion of a Charged Particle in an Electric Field
| Quantity | Formula |
|---|---|
| Force on charge | $\vec{F} = q\vec{E}$ |
| Acceleration | $a = \dfrac{qE}{m}$ |
| Velocity (from rest) | $v = \dfrac{qE}{m}t$ |
| Displacement (from rest) | $s = \dfrac{1}{2} a t^2$ |
| Trajectory | $y = \dfrac{1}{2}\left(\dfrac{qE}{m}\right)\left(\dfrac{x}{u_x}\right)^2$ |
Nature of the Trajectory and Examples
The parabolic trajectory of a charged particle in a uniform electric field is critical for analyzing applications such as cathode ray tubes and mass spectrometers. The deviation of the path depends on charge, mass, and field strength.
For additional practice with electrostatics, visit Electrostatics Mock Test 1.
Combined Electric and Magnetic Fields
When both electric and magnetic fields act on a charged particle, the total force is the Lorentz force: $\vec{F} = q(\vec{E} + \vec{v} \times \vec{B})$. The resulting trajectory depends on the orientation and magnitudes of the fields and particle velocity.
Such scenarios can lead to circular, helical, or complex motions, forming the basis for devices like velocity selectors.
Effects of Electric Field Strength and Particle Properties
The amount of deflection and acceleration in an electric field is affected by the particle's charge-to-mass ratio ($q/m$) and the field strength ($E$). Larger $q/m$ or stronger fields yield greater curvature in the particle's path.
For continuous equipotential conditions related to such fields, refer to Equipotential Surface.
Summary of Motion of a Charged Particle in an Electric Field
- Force on a charge: $\vec{F} = q\vec{E}$ in uniform field
- Acceleration: $a = \dfrac{qE}{m}$, constant value
- Trajectory is parabolic if initial velocity is perpendicular
- Direction of motion depends on particle charge sign
- Combined electric and magnetic fields yield complex paths
- Displacement and velocity formulas follow kinematic equations
- Applications include CRTs and particle detectors
Understanding the movement of a charged particle in an electric field is crucial for analyzing motion in devices and natural phenomena. For more on related kinetic theory principles, see Kinetic Theory Of Gases.
FAQs on Understanding the Motion of a Charged Particle in an Electric Field
1. What is the motion of a charged particle in a uniform electric field?
The motion of a charged particle in a uniform electric field is typically parabolic if it enters the field at an angle and linear if it enters parallel to the field. The key points include:
- Charged particles experience a constant force in the direction of the electric field.
- The acceleration depends on the charge-to-mass ratio (q/m).
- If the initial velocity is perpendicular to the field, the path forms a parabola, similar to projectile motion.
- If the initial velocity is parallel or antiparallel to the field, the particle moves in a straight line, accelerating or decelerating depending on the charge's sign.
2. How does a positively charged particle move in an electric field?
A positively charged particle moves in the direction of the electric field lines. Specifically:
- The particle accelerates along the electric field direction.
- The velocity of the particle increases if it moves with the field, decreases if opposite.
- The path taken depends on the initial velocity direction (linear or parabolic).
3. What is the force on a charged particle in an electric field?
The force (F) on a charged particle in an electric field (E) is given by the equation F = qE. Important points include:
- q is the charge of the particle.
- E is the magnitude of the electric field.
- The direction of force depends on the sign of q (positive or negative).
4. What is the trajectory of a charged particle in an electric field if its initial velocity is perpendicular to the field?
The trajectory of a charged particle with initial velocity perpendicular to the electric field is a parabola. Key details:
- The particle experiences constant acceleration along the field.
- Its velocity components perpendicular and parallel to the field combine, forming a parabolic path.
- This scenario is similar to projectile motion under gravity, as per NCERT/CBSE Physics.
5. What factors affect the motion of a charged particle in an electric field?
The main factors affecting the motion of a charged particle in an electric field are:
- Magnitude and direction of the electric field.
- Charge (q) and mass (m) of the particle.
- Initial velocity (magnitude and direction).
- Nature (positive or negative) of the charge.
6. What is the equation of motion for a charged particle in a uniform electric field?
The equation of motion for a charged particle in a uniform electric field is similar to kinematic equations with constant acceleration:
- Acceleration: a = F/m = qE/m
- Vertical position: y = (qE/2m)t²
- Horizontal position (if initial velocity u_x): x = uxt
7. Is the electric field always uniform? How does non-uniformity affect the motion?
The electric field is not always uniform; non-uniform fields cause variable acceleration of the charged particle.
- In a uniform field, the force and acceleration are constant, leading to predictable motion (linear or parabolic).
- In a non-uniform field, the particle's acceleration changes with position, making its path more complex (curved, not parabolic).
- Understanding both scenarios is important for CBSE/NCERT exams.
8. Can a charged particle move at a constant velocity in an electric field?
No, a charged particle cannot move at constant velocity in an electric field because it experiences a constant force.
- The force causes continuous acceleration or deceleration.
- Only if the net force is zero (for instance, opposing fields or zero charge), can velocity remain constant.
- This principle is part of the CBSE Physics understanding of dynamics in fields.
9. What happens to an electron when placed in a uniform electric field?
An electron, being negatively charged, moves opposite to the direction of the electric field lines.
- It accelerates towards higher potential.
- The motion is linear or parabolic depending on initial velocity.
- This is a key example for motion of charged particles in CBSE Syllabus.
10. How is the energy of a charged particle affected as it moves in an electric field?
The energy of a charged particle in an electric field changes due to work done by or against the electric field.
- Potential energy decreases if the charge moves along the field direction (for positive charge).
- Kinetic energy increases due to acceleration provided by the field.
- The total energy remains conserved (ignoring non-conservative forces).
























