




How Do You Calculate and Apply Projectile Motion Equations?
Projectile motion refers to the motion of an object projected into the air, moving under the influence of gravity alone. The trajectory followed by such an object is parabolic when air resistance and other external factors are neglected. Understanding projectile motion is essential for solving kinematics problems in physics, especially in JEE Main preparation.
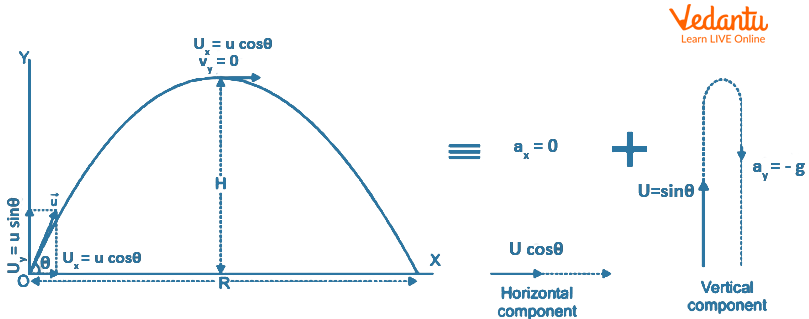
Definition and Basic Features of Projectile Motion
A projectile is any object that is thrown or projected with some initial velocity and thereafter moves under the influence of gravity, with no propulsion from other forces. The analysis typically ignores air resistance and Earth's rotation, and assumes gravity acts with constant magnitude and direction throughout the motion.
The path traced by a projectile is called its trajectory. This trajectory is always a parabola if the motion occurs near Earth's surface and the only force acting is gravity. The horizontal component of velocity remains unchanged due to the absence of horizontal forces, and the vertical component changes uniformly due to gravity.
Projectile motion can be considered a two-dimensional motion because it involves simultaneous movement in both horizontal and vertical directions. The study of such motion falls under the broader category of Motion In 2D Dimensions.
Types of Projectile Motion
Projectile motion is mainly classified into two types based on the angle of projection. The first type is horizontal projectile motion, where the object is projected horizontally from a certain height. The second is oblique projectile motion, where the object is projected with an initial velocity at an angle with respect to the horizontal.
- Horizontal projectile motion: projection angle is $0^\circ$
- Oblique projectile motion: projection angle is between $0^\circ$ and $90^\circ$
In both cases, the acceleration due to gravity acts only in the vertical direction, and no force acts in the horizontal direction. For advanced situations, such as motion on an inclined surface, refer to Projectile On An Inclined Plane.
Resolution of Initial Velocity
The initial velocity $u$ of a projectile can be resolved into two perpendicular components. The horizontal component is $u_x = u \cos\theta$, and the vertical component is $u_y = u \sin\theta$, where $\theta$ is the angle of projection with the horizontal.
These components allow the analysis of motion separately along each axis. The horizontal component ($u_x$) remains constant throughout the motion, while the vertical component ($u_y$) changes linearly with time because of gravity. This is fundamental in Kinematics Overview.
Equations of Motion for Projectile
The horizontal position $x$ and vertical position $y$ of the projectile at any time $t$ are given by the equations:
$x = u \cos\theta \cdot t$
$y = u \sin\theta \cdot t - \dfrac{1}{2} g t^2$
Here, $g$ is the acceleration due to gravity (approximately $9.8 \ \text{m/s}^2$ downward). The shape of the trajectory can be obtained by eliminating $t$ from these equations, resulting in the equation of a parabola. The graphical interpretation of position and velocity is explained in detail in Displacement And Velocity Graphs.
Time of Flight
The time of flight is the total time a projectile remains in the air. For a projectile launched from ground level and landing at the same level, the time of flight $T$ is given by:
$T = \dfrac{2u \sin\theta}{g}$
This expression is derived by using the condition that the vertical displacement is zero when the projectile lands. The time of flight depends directly on the initial velocity and the sine of the angle of projection.
Horizontal Range
The horizontal range $R$ is the horizontal distance covered by the projectile during the entire motion. It is given by:
$R = u \cos\theta \cdot T = \dfrac{u^2 \sin 2\theta}{g}$
The range is maximum when $\sin 2\theta = 1$, which occurs at $\theta = 45^\circ$. Thus, for a given speed, the maximum range is $R_{\text{max}} = \dfrac{u^2}{g}$.
| Parameter | Expression |
|---|---|
| Time of Flight ($T$) | $\dfrac{2u\sin\theta}{g}$ |
| Horizontal Range ($R$) | $\dfrac{u^2\sin2\theta}{g}$ |
| Maximum Height ($H$) | $\dfrac{u^2 \sin^2\theta}{2g}$ |
Maximum Height of Projection
The maximum height $H$ is the highest vertical position reached by the projectile. At this point, the vertical component of the velocity becomes zero. The maximum height is given by:
$H = \dfrac{u^2 \sin^2\theta}{2g}$
This height is greatest when $\theta = 90^\circ$ for a given speed. At this angle, the motion becomes a vertical projectile, and $H_{\text{max}} = \dfrac{u^2}{2g}$.
Key Assumptions in Projectile Motion
The analysis of projectile motion is based on certain ideal assumptions. Air resistance is neglected, the acceleration due to gravity is constant and acts vertically downward, and effects due to Earth's curvature and rotation are ignored. These assumptions simplify calculations and make theoretical analysis feasible.
- Gravity acts uniformly and downward
- No air resistance is considered
- Earth's curvature is neglected
Understanding these assumptions is critical for solving standard projectile motion problems in JEE and for topics such as Instantaneous Velocity.
Common Equations Used in Projectile Motion
Projectile motion uses several standard equations. The key quantities—displacement, velocity, time of flight, range, and maximum height—are all derived from basic kinematic equations split into horizontal and vertical components. Mastery of these equations is essential for problem-solving.
- Horizontal: $x = u \cos\theta \cdot t$
- Vertical: $y = u \sin\theta \cdot t - \dfrac{1}{2}gt^2$
- Range: $R = \dfrac{u^2 \sin 2\theta}{g}$
- Time: $T = \dfrac{2u \sin\theta}{g}$
- Max height: $H = \dfrac{u^2 \sin^2\theta}{2g}$
Typical Problems Involving Projectile Motion
JEE-level problems on projectile motion involve calculating time of flight, range, and maximum height under standard assumptions. Complex situations, such as motion on inclined planes or varying initial conditions, also appear. Practice with projectile motion problems improves conceptual clarity and application skills. For additional practice, students can refer to Kinetic Energy Of A Rotating Body for related kinematics concepts.
FAQs on Understanding Projectile Motion in Physics
1. What is projectile motion?
Projectile motion refers to the curved path an object follows when it is thrown or launched near the surface of the Earth, influenced only by gravity and its initial velocity.
Key points about projectile motion:
- It involves both horizontal and vertical components of motion.
- The horizontal velocity remains constant (if air resistance is neglected).
- The vertical motion is affected by gravitational acceleration.
- The typical trajectory is a parabola.
2. What are the main characteristics of projectile motion?
Projectile motion has distinct features:
- Two-dimensional motion: Involves independent horizontal and vertical components.
- Constant horizontal velocity: No horizontal acceleration if air resistance is ignored.
- Vertical acceleration: Constant acceleration downwards due to gravity (g = 9.8 m/s²).
- Parabolic path: The trajectory follows a parabolic shape.
3. What are the equations used in projectile motion?
The key equations of projectile motion help calculate position, time, and range:
- Horizontal displacement (x): x = ux t
- Vertical displacement (y): y = uy t - (1/2) g t²
- Time of flight (T): T = (2u sinθ) / g
- Maximum height (H): H = (u² sin²θ) / (2g)
- Horizontal range (R): R = (u² sin2θ) / g
4. What factors affect the range of a projectile?
The range of a projectile depends on several key factors:
- Initial velocity (u): Higher velocity increases range.
- Angle of projection (θ): Range is maximum at 45°.
- Acceleration due to gravity (g): Greater gravity reduces range.
- Height of projection: Launching from a height affects range.
5. How do you calculate the maximum height reached by a projectile?
The maximum height (H) is the highest point reached during projectile motion:
- Formula: H = (u² sin²θ) / (2g), where:
- u = Initial velocity
- θ = Angle of projection
- g = Acceleration due to gravity
6. Why does a projectile follow a parabolic path?
A projectile follows a parabolic path because its horizontal and vertical motions are independent, and gravity acts only downwards.
- Horizontal velocity remains constant.
- Vertical motion is uniformly accelerated due to gravity.
- Combining these motions results in a parabola.
7. What is the difference between horizontal and angular projectile motion?
The main difference is in the angle of projection:
- Horizontal projectile motion: The object is launched horizontally (θ = 0°) and has no initial vertical velocity.
- Angular projectile motion: The object is launched at an angle (θ > 0°), so it has both horizontal and vertical components.
8. How does gravity influence projectile motion?
Gravity acts as the only force influencing vertical motion in a projectile:
- It causes the vertical acceleration downwards (g = 9.8 m/s²).
- It affects vertical velocity and displacement.
- It determines the time of flight, range, and maximum height.
9. What are some real-life examples of projectile motion?
Real-life examples of projectile motion include:
- A ball thrown in the air
- A basketball shot
- Long jump in athletics
- A cannonball fired
- Water sprayed from a hose
10. What is the time of flight for a projectile?
The time of flight is the total duration a projectile remains in the air:
- Formula: T = (2u sinθ) / g
- Depends on initial velocity u, angle of projection θ, and g (9.8 m/s²)
- For projectiles launched from the ground and returning to the same level.
11. What are the assumptions made in derivation of equations of projectile motion?
Key assumptions for projectile motion equations are:
- Air resistance is neglected.
- Acceleration due to gravity (g) is constant and acts vertically downward.
- Earth’s curvature and rotation are ignored.
























