




What Determines the Speed of Electromagnetic Waves?
The speed of electromagnetic waves is a fundamental physics concept crucial for understanding light and wireless communication.
Electromagnetic waves move through space as oscillating electric and magnetic fields, always perpendicular to each other and the direction of propagation.
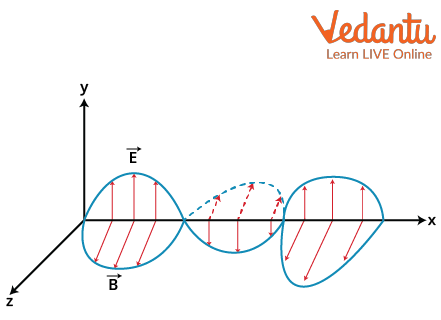
What Is the Speed of Electromagnetic Waves?
The speed of electromagnetic (EM) waves in a vacuum is exactly $c = 3 \times 10^8$ m/s, which is also referred to as the speed of light.
In a medium other than vacuum, this speed changes based on the optical properties, especially the refractive index, denoted as $n$.
For instance, in air, the speed of electromagnetic waves is only slightly less than $c$, making air almost as transparent as vacuum for most calculations.
Just like sound waves described in Speed Of Sound Waves In Air, EM wave speed depends on the medium, but EM waves require no medium at all.
Visualization and Real-Life Analogy
Imagine dropping a stone in a perfectly calm pond; the ripples spread out evenly. EM waves act like these ripples in space, radiating energy away at constant speed.
Visualizing the electric and magnetic fields as two synchronized, perpendicular waves moving forward helps grasp how the wave propagates without physical particles.
Mathematical Formula for Speed of Electromagnetic Waves
In a vacuum, the speed is given by the relationship $c = \dfrac{1}{\sqrt{\varepsilon_0 \mu_0}}$, where $\varepsilon_0$ is permittivity and $\mu_0$ is permeability.
Within any medium, the formula modifies to $v = \dfrac{1}{\sqrt{\varepsilon \mu}}$, where $\varepsilon$ and $\mu$ are properties of the medium.
If the refractive index is $n$, the speed in the medium is $v = \dfrac{c}{n}$, showing the inverse relation between speed and optical density.
Comparing Speed in Different Media
| Medium | Speed (m/s) |
|---|---|
| Vacuum (free space) | $3.00 \times 10^8$ |
| Air | $\approx 2.99 \times 10^8$ |
| Water | $2.25 \times 10^8$ |
| Glass | $2.00 \times 10^8$ |
Understanding this table is vital for optics questions and for technologies like fiber-optics in Communication Systems.
Key Characteristics of Electromagnetic Wave Speed
- Speed in vacuum is always $3 \times 10^8$ m/s
- Speed decreases in denser media (higher $n$)
- Independent of wave’s frequency or intensity in the same medium
- Applicable for radio, light, X-rays, and gamma rays alike
You can further explore EM wave characteristics in Electromagnetic Spectrum for a broader picture of types and uses.
Application and Relevance for JEE & NEET
Knowing the fixed speed of EM waves underpins all calculations involving light, radio waves, and advanced topics in Wave Particle Duality.
This helps distinguish electromagnetic waves from mechanical waves, deepening understanding ahead of topics like Oscillations And Waves.
Solved Example: Speed of EM Waves in a Medium
An EM wave travels in glass ($n = 1.5$). Find its speed. We use $v = \dfrac{c}{n}$, so $v = \dfrac{3.0 \times 10^8}{1.5} = 2.0\times 10^8$ m/s.
If asked to relate wavelength and frequency: $c = \lambda \nu$ in vacuum, while in a medium, $v = \lambda_{\text{med}} \nu$.
Practice Question
A light wave enters water with $n = 1.33$. Calculate its speed in the water using $c = 3.0 \times 10^8$ m/s.
Common Student Mistakes
- Assuming speed changes with frequency or intensity (it does not)
- Forgetting the role of refractive index ($n$) when shifting media
- Confusing EM wave speed with sound wave speed
Wave formulas from Progressive Harmonic Wave can clarify relationships between speed, wavelength, and frequency.
Text-Based Related Topics for Revision
- Wave equation and its derivation
- Properties of light and optical phenomena
- Relation between electric and magnetic fields in wave propagation
- Calculating refractive index and its significance
- Polarization and electromagnetic spectrum analysis
FAQs on Understanding the Speed of Electromagnetic Waves
1. What is the speed of electromagnetic waves in a vacuum?
The speed of electromagnetic waves in a vacuum is a constant value of approximately 3 x 108 m/s (meters per second).
Key points:
- This value is known as the speed of light (c).
- It applies to all types of electromagnetic waves like light, radio waves, microwaves, X-rays, and gamma rays.
- In symbols: c = 3 x 108 m/s.
2. Why do all electromagnetic waves have the same speed in vacuum?
All electromagnetic waves travel at the same speed in a vacuum because their speed depends only on the electric permittivity (ε0) and magnetic permeability (μ0) of free space.
Key reasons:
- No material medium to cause resistance or dispersion
- All EM waves are produced by the oscillation of electric and magnetic fields
- Speed determined by: c = 1 / √(μ0ε0)
3. How is the speed of electromagnetic waves mathematically derived?
The speed of electromagnetic waves is obtained from Maxwell’s equations, resulting in:
- c = 1 / √(μ0ε0)
- Where μ0 = permeability of free space
- And ε0 = permittivity of free space
4. Do electromagnetic waves travel at different speeds in different media?
Yes, electromagnetic waves slow down when traveling through materials such as water, glass, or air.
Key facts:
- In a vacuum, speed is maximum (3 x 108 m/s).
- In denser media, speed decreases due to interaction with particles.
- Formula: v = c/n, where n is the refractive index of the medium.
5. Which types of waves are classified as electromagnetic waves?
Electromagnetic waves include all waves that do not require a material medium for propagation.
Main types include:
- Radio waves
- Microwaves
- Infrared rays
- Visible light
- Ultraviolet rays
- X-rays
- Gamma rays
6. What factors affect the speed of electromagnetic waves?
The major factor that affects the speed of electromagnetic waves is the medium they pass through.
Details:
- In vacuum: Speed is constant at 3 x 108 m/s
- In material media: Speed decreases, depending on the medium’s refractive index
7. What is the relation between wavelength, frequency, and speed of electromagnetic waves?
For electromagnetic waves, the relation is:
Speed (v) = Frequency (f) × Wavelength (λ)
- In vacuum, v = c
- If one increases, the other decreases (for constant speed)
8. Why are electromagnetic waves called non-mechanical waves?
Electromagnetic waves are called non-mechanical waves because they do not require a material medium to travel.
- They can move through vacuum (empty space)
- They arise from oscillating electric and magnetic fields
9. Who first measured the speed of electromagnetic waves?
The speed of electromagnetic waves (or light) was first measured by Ole Römer in the 17th century.
Details:
- James Clerk Maxwell later theoretically established the speed through formulae.
- Further precision came with Hertz’s experiments and modern measurements.
10. What is the significance of the constant speed of light in physics?
The constant speed of light (c) is fundamental to physics because:
- It is a universal constant for all electromagnetic waves in vacuum
- Acts as the foundation for Einstein’s theory of relativity
- Is used to define the meter (SI unit of length)
- Affects time, space, and causality in physics
























