Superposition of SHM (Simple Harmonic Motion) for JEE

Simple harmonic motion or SHM is an oscillatory type of motion in which the particle or body is continuously subjected to a retarding force which is proportional to the displacement of the particle from the equilibrium position. Some examples of simple harmonic motion are the pendulum, swing, car shock absorber, sound waves, and much more.

Talking about SHM in sound waves, we can visualise a wave in which at each point, a particle is performing SHM from its equilibrium position. The resulting pattern of SHM gives waves. Now, let us take a scenario in which two waves approach each other and get joined. In that case, we get a new wave. This process is called the superposition of SHM. Superposition of SHM implies the algebraic sum of two or more waves to get a final wave. Depending upon the wavelength, amplitude, and frequency, the final wave can be stronger or weaker or it can be a beat.

Principle of Superposition of SHM

According to the principle of superposition of SHM, the resultant displacement of a number of waves in a medium at a particular point is the vector sum of the individual displacements produced by each of the waves at that point. 

Suppose that there are n waves

$({\overrightarrow{y}}_1,{\overrightarrow{y}}_2,{\overrightarrow{y}}_3,...,{\overrightarrow{y}}_n)$. 

When all such waves superimpose, we get a resultant wave as

${\overrightarrow{y}}_{res}={\overrightarrow{y}}_1+{\overrightarrow{y}}_2+{\overrightarrow{y}}_3+...+{\overrightarrow{y}}_n$

A wave equation is of the form $\overrightarrow{y}=\overrightarrow{A}\sin (\omega t-kx)$, where A is the amplitude, k is the wave number, $\omega$ is the wave frequency, t is the time, and $x$ is the displacement. For waves to superimpose, the wave frequencies may or may not be the same.

Superposition can be visualised by a wave on a stretched string. Suppose two waves flowing towards each other on a stretched string. When they touch each other, a new wave is formed. That new wave is the superimposed wave.

Superposition of Two SHM with Same Frequency

Consider two waves having the same angular frequency.

${\overrightarrow{y}}_1={\overrightarrow{A}}_1\sin \left(\omega t\right)$

${\overrightarrow{y}}_2={\overrightarrow{A}}_2\sin (\omega t+\theta )$

According to the superposition principle, the resultant wave is given by $\overrightarrow{y}={\overrightarrow{y}}_1+{\overrightarrow{y}}_2$.

$y_1+y_2=A_1\sin \omega t+A_2\sin (\omega t+\theta )$

$y=A\sin (\omega t+\alpha )$

Use the trigonometric formula $\sin (A+B)=\sin A\cos B+\cos A\sin B$ and compare the equations to find A and $\alpha$.

$A\sin (\omega t+\alpha )=A_1\sin \omega t+A_2\sin (\omega t+\theta )$

$A(\sin \omega t\cos \alpha +\cos \omega t\sin \alpha )=A_1\sin \omega t+A_2(\sin \omega t\cos \theta +\cos \omega t\sin \theta )$

$(A\cos \alpha )\sin \omega t+(A\sin \alpha )\cos \omega t=(A_1+A_2\cos \theta )\sin \omega t+(A_2\sin \theta )\cos \omega t$

Comparing both sides, we get,

$A\cos \alpha =A_1+A_2\cos \theta$

$A\sin \alpha =A_2\sin \theta$

Squaring and adding both the above equations, we will get

${(A\sin \alpha )}^2+{(A\cos \alpha )}^2={(A_1+A_2\cos \theta )}^2+{(A_2\sin \theta )}^2$

$A^2=A_1^2+A_2^2+2A_1{A}_2\cos \theta$

$A=\sqrt{A_1^2+A_2^2+2A_1{A}_2\cos \theta }$

And, dividing the second equation by the first one, we will get

$\tan \alpha =\frac{A_2\sin \theta }{A_1+A_2\cos \theta }$

Superposition of Two SHM with Different Frequency

Consider two waves having different angular frequencies

$y_1=A\sin {\omega }_{1}t$

$y_2=A\sin {\omega }_{2}t$

According to the superposition principle, the resultant wave is given by $\overrightarrow{y}={\overrightarrow{y}}_1+{\overrightarrow{y}}_2$.

$y=A\sin {\omega }_{1}t+A\sin {\omega }_{2}t$

$y=A(\sin {\omega }_{1}t+\sin {\omega }_{2}t)$

Now, here we will use the trigonometric identity $\sin A+\sin B=2\sin \left(\frac{A+B}{2}\right)\cos \left(\frac{A-B}{2}\right)$

The new wave equation will be

$y=A(\sin {\omega }_{1}t+\sin {\omega }_{2}t)$

$y=2A\cos \left(\frac{{\omega }_1-{\omega }_2}{2}t\right)\sin \left(\frac{{\omega }_1+{\omega }_2}{2}t\right)$

This oscillatory motion has angular frequency of $\frac{{\omega }_1+{\omega }_2}{2}$ and amplitude $2A\cos \left(\frac{{\omega }_1-{\omega }_2}{2}\right)t$.

Clearly, the amplitude of the oscillating motion is time-dependent. Such an amplitude is called modulated amplitude $A_m$. The resulting equation is

$y=A_m\sin \left(\frac{{\omega }_1+{\omega }_2}{2}\right)t$

Beats

In the above case, we see that the frequencies of the waves are different. When there is a difference in the frequencies, then this gives rise to beats. The general formula of beats is $f_{beat}=|f_1-f_2|$.

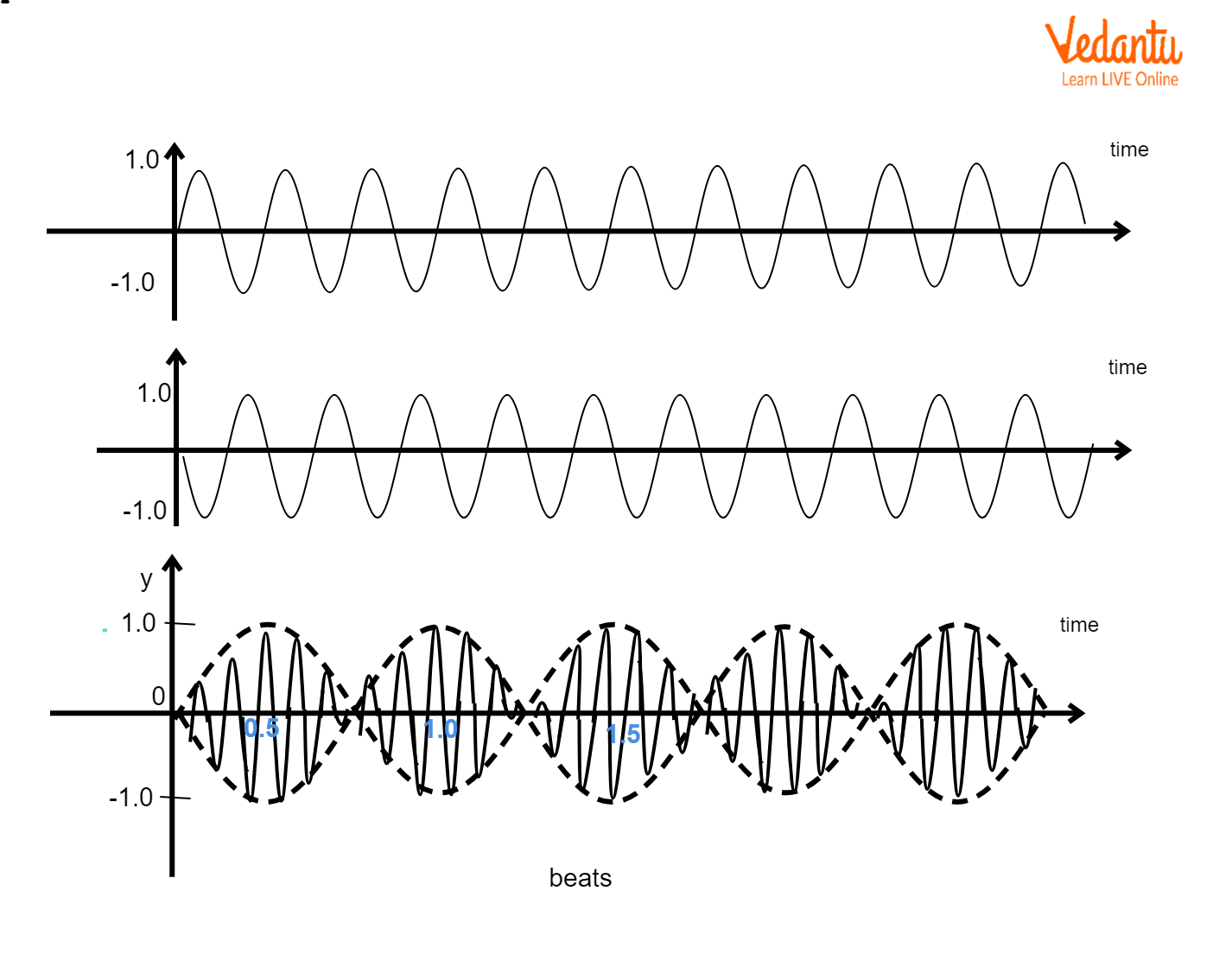
Beats

Superposition of Three SHM

Consider three waves having equal phase differences

$y_1=A_1\sin (\omega t-\varphi )$

$y_2=A_2\sin \omega t$

$y_3=A_3\sin (\omega t+\varphi )$

Using the principle of superposition of waves, the resultant wave equation will be

$y=y_1+y_2+y_3$

$y=A_1\sin (\omega t-\varphi )+A_2\sin \omega t+A_3\sin (\omega t+\varphi )$

$y=A\sin (\omega t+\alpha )$

Now, expand the second step and the third step and compare

$A(\sin \omega t\cos \alpha +\cos \omega t\sin \alpha )=A_1(\sin \omega t\cos \varphi -\cos \omega t\sin \varphi )+A_2\sin \omega t+A_3(\sin \omega t\cos \varphi +\cos \omega t\sin \varphi )$

$(A\cos \alpha )\sin \omega t+(A\sin \alpha )\cos \omega t=(A_1\cos \varphi +A_2+A_3\cos \varphi )\sin \omega t+(A_3\sin \varphi -A_1\sin \varphi )\cos \omega t$

On comparing, we will get

$A\cos \alpha =A_1\cos \varphi +A_2+A_3\cos \varphi$

$A\sin \alpha =A_3\sin \varphi -A_1\sin \varphi$

Squaring and adding the two equations,

$A^2=A_1^2{\cos }^2\varphi +A_2^2+A_3^2{\cos }^2\varphi +2A_1{A}_2\cos \varphi +2A_2{A}_3\cos \varphi +2A_1{A}_3{\cos }^2\varphi +A_3^2{\sin }^2\varphi +A_1^2{\sin }^2\varphi -2A_1{A}_3{\sin }^2\varphi$

$A^2=A_1^2+A_2^2+A_3^2+2A_1{A}_2\cos \varphi +2A_2{A}_3\cos \varphi +2A_1{A}_3\cos 2\varphi$

$A=\sqrt{A_1^2+A_2^2+A_3^2+2A_1{A}_2\cos \varphi +2A_2{A}_3\cos \varphi +2A_1{A}_3\cos 2\varphi }$ 

Divide the second equation by the first equation,

$\tan \alpha =\frac{A_3\sin \varphi -A_1\sin \varphi }{A_1\cos \varphi +A_2+A_3\cos \varphi }$

So, these equations will give us the amplitude and phase difference of the final wave.

Phasor Diagrams

The resultant of the interfering waves can also be found out by using the phasor diagram.

Suppose we have two wave equations

$y_1=a\sin \omega t$ 

$y_2=b\sin (\omega t+\varphi )$ 

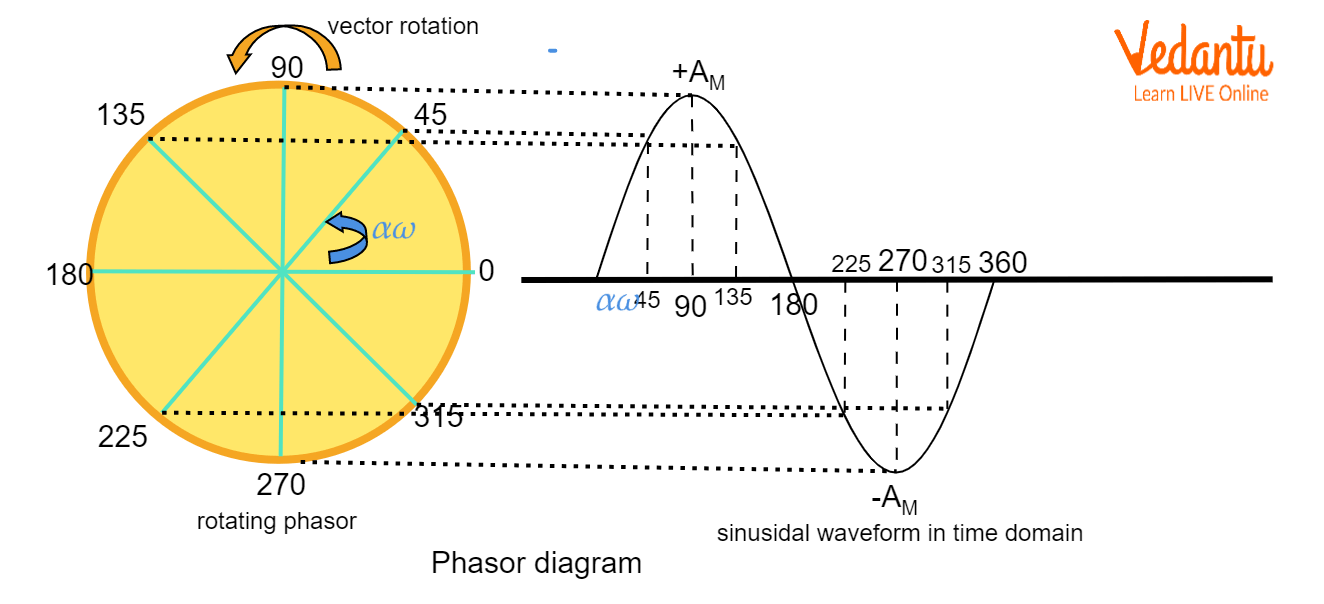
Phasor Diagram

The phase difference is $\varphi$. On the phasor diagram, we will make two vectors having angles between them of $\varphi$. Their magnitudes will be equal to the amplitudes. Using the vector addition, we can find the resultant amplitude and resultant phase difference. In the phase diagram, one axis is taken as the reference axis and the phase differences are taken according to that axis.

Similarly, we can find the resulting equations of more than two waves or up to N waves.

Conclusion

In waves, the particles at each and every point perform simple harmonic motion. That is why waves are the best example of simple harmonic motion. When two or more waves come in contact with each other, they join up and give a resultant wave. This process is called the Superposition of waves or Superposition of simple harmonic waves.

The nature of resulting waves depends upon the type of waves interfering with each other. If the waves have the same frequencies but different amplitudes, then the resulting wave also has the same frequency but the resulting amplitude is the vector sum of the waves. If the amplitudes are the same but frequencies are different, the result is the formation of beats. Similarly, we can find the resulting equations of more than three interfering waves or up to N interfering waves.