JEE Advanced 2023 Revision Notes for Vectors

Scalar Quantity:

A quantity that has only magnitude and is not related to any direction is called a scalar quantity.

For example Mass, length, time, Temperature, Area volume, Speed, Density work, etc.

Vector Quantity:

A quantity which has magnitude and also a direction space is called a vector quantity.

For example, Displacement, Velocity, Acceleration, Force, Torque etc.

Linearly Independent and Dependent Vectors:

• A set of vectors ${\overrightarrow a _1},{\overrightarrow a _2},............,{\overrightarrow a _n}$  is said to be linearly independent if

${x_1}{\overrightarrow a _1} + {x_2}{\overrightarrow a _2} + ............ + {x_n}{\overrightarrow a _n} = 0$ 

$\Rightarrow {x_1} = {x_2} = .....{x_n} = 0$ 

• A set of vectors${\overrightarrow a _1},{\overrightarrow a _2},............,{\overrightarrow a _n}$ is said to be linearly dependent if there exists scalars ${x_1},{x_2},......,{x_n}$ not all zero such that 

${x_1}{\overrightarrow a _1} + {x_2}{\overrightarrow a _2} + ............ + {x_n}{\overrightarrow a _3} = 0$ . 

Collinearity:

• Two vectors ${\overrightarrow a _1}$ and ${\overrightarrow a _2}$ are collinear $\Leftrightarrow {\overrightarrow a _1} = \lambda {\overrightarrow a _2}$ for some scalar $\lambda$ .

• Three vectors ${\overrightarrow a _1}$ ,${\overrightarrow a _2}$ and ${\overrightarrow a _3}$ are collinear, If there exists scalars $x,y,z$ such that 

$x{\overrightarrow a _1} + y{\overrightarrow a _2} + z{\overrightarrow a _n} = 0$  where $x + y + z = 0$ 

Also the points $A,B,C$ are collinear if $\overrightarrow {AB}  = \lambda \overrightarrow {BC}$ for some scalar $\lambda$ .

Coplanarity:

• Three vectors ${\overrightarrow a _1}$ ,${\overrightarrow a _2}$ and ${\overrightarrow a _3}$ are coplanar if one of them is a liner combination of the other two if there exist scalar $x$ and $y$ such that $\overrightarrow {{a_3}}  = x\overrightarrow {{a_1}}  + y\overrightarrow {{a_2}}$ 

• Four vectors${\overrightarrow a _1}$ ,${\overrightarrow a _2}$ ,$\overrightarrow {{a_3}}$ and $\overrightarrow {{a_4}}$ are coplanar if scalars $x,y,z,w$ not all zero simultaneously such that 

$x\overrightarrow {{a_1}}  + y\overrightarrow {{a_2}}  + z\overrightarrow {{a_3}}  + w\overrightarrow {{a_4}}  = 0$ Where $x + y + z + w = 0$ 

Null Vector or Zero Vector:

If a vector's initial and terminal points coincide, it is called a zero vector. It is denoted by $\overrightarrow 0$ or 0. Its magnitude is zero and direction indeterminate.

Unit Vector:

A vector whose magnitude is of unit length along any vector$\overrightarrow a$ is called a unit vector in the direction of $\overrightarrow a$ and is denoted by $\hat a$.

Reciprocal Vector:

A vector whose direction is same as that of given vector $\overrightarrow a$ but its magnitude is the reciprocal of the magnitude of the given vector$\overrightarrow a$ is called the reciprocal of $\overrightarrow a$ and is denoted by ${a^{ - 1}}$ 

Thus if $\overrightarrow a  = a.\hat a$ then ${a^{ - 1}} = \dfrac{1}{a}\hat a$ 

Equal Vector:

Two non-zero vectors are said to be equal if their magnitudes are equal and directions are the same. They act parallel to each other in the same direction.

Negative Vector: 

The negative of a vector is defined as the vector having the same magnitude but opposite direction.

For example if $\overrightarrow a  = \overrightarrow {PQ}$ , then the negative of $\overrightarrow a$ is the vector $\overrightarrow {QP}$ and is denoted as $\overrightarrow {- a}$ .

Like and Unlike Vector:

Collinear vectors with the same direction are known as like vectors, while those with opposite directions are known as unlike vectors.

For example, the vector given in the figure.

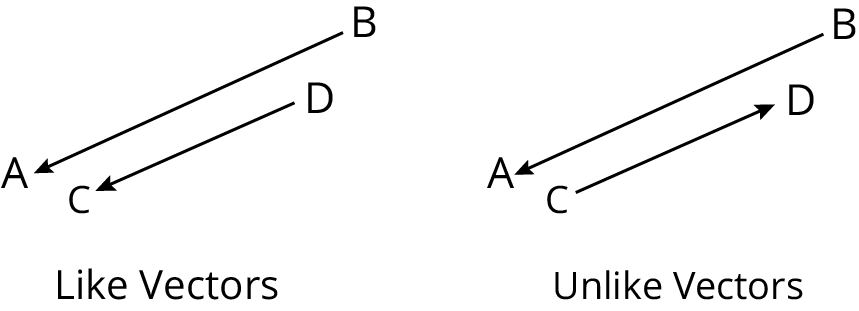
Like and Unlike Vectors

Localised Vector and Free Vector:

A vector is drawn parallel to a given vector through a specified point as the initial point is known as a localised vector. If the initial point of a vector is not specified, it is said to be a free vector.

Position Vector: 

Let O be the origin and A be a point such that $\overrightarrow {OA}  = \overrightarrow a$ then, we say that the position vector of A is $\overrightarrow a $.

Representation of Vectors: 

Directed line segments represent vectors. A vector $\overrightarrow a$ is represented by the directed line segment $\overrightarrow {AB}$. The magnitude of vector $\overrightarrow a$ is equal to $AB$, and the direction of vector $\overrightarrow a$ is along the line from $A$ to $B$.

Representation of Vector

Addition of Vector:

• Let $\overrightarrow a$ and $\overrightarrow b$ be any two vectors. From the terminal point of $\overrightarrow a$, vector $\overrightarrow b$ is drawn. Then the vector from the initial point O of $\overrightarrow a$ to the terminal point Q of $\overrightarrow b$ is called the sum of vectors $\overrightarrow a$ and $\overrightarrow b$ and is denoted by $\overrightarrow a  + \overrightarrow b$ this is called the triangle law of addition of vectors.
  
  

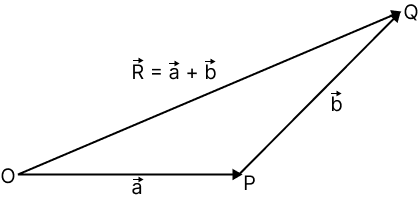
Triangle Law of Addition

Properties of Vector Addition:

• Vector addition is commutative $\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a$ .

• Vector addition is associative $\overrightarrow a  + (\overrightarrow b  + \overrightarrow c ) = \overrightarrow {(a}  + \overrightarrow {b)}  + \overrightarrow c$ .

• $\overrightarrow O  + \overrightarrow a  = \overrightarrow a  + \overrightarrow O  = \overrightarrow a$  So the zero vector is additive identity.

• $\overrightarrow a  + ( - \overrightarrow a ) = \overrightarrow O  = ( - \overrightarrow {a)}  + \overrightarrow a$  So the additive inverse of$\overrightarrow a$ is $- \overrightarrow a$ .

Addition of Any Number of Vectors:  

To find the sum of any number of vectors by a directed line segment with the terminal point of the previous vector as the initial point of the next vector. Then the line segment joining the initial point of the first vector to the terminal point of the last vector will represent the sum of the vectors:

Thus if, $\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {AB}  = \overrightarrow b ,\overrightarrow {BC}  = \overrightarrow c, \overrightarrow {CD} = \overrightarrow d ,\overrightarrow {DE}  = \overrightarrow e$ and $\overrightarrow {EF}  = \overrightarrow f$ then 

$\overrightarrow a  + \overrightarrow b  + \overrightarrow c  + \overrightarrow d  + \overrightarrow e  + \overrightarrow f  = \overrightarrow {OA}  + \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {DE}  + \overrightarrow {EF}  = \overrightarrow {OF}$ 

If the terminal point F of the last vector coincide with the initial point of the first vector then

$\overrightarrow a  + \overrightarrow b  + \overrightarrow c  + \overrightarrow d  + \overrightarrow e  + \overrightarrow f  = \overrightarrow {OA}  + \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {DE}  + \overrightarrow {EO}  = \overrightarrow O$ 

The sum of vectors is zero or null in this case.

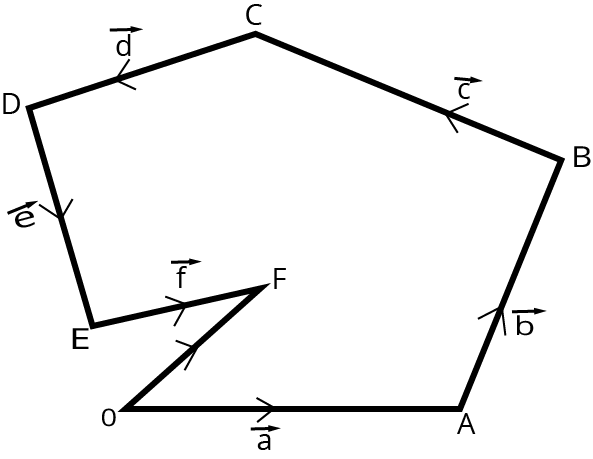
Addition of Any Number of Vectors

Difference of Vectors:

If $\overrightarrow a$ and$\overrightarrow b$ be any two vectors, then their difference $\overrightarrow a  - \overrightarrow b$  is defined as $\overrightarrow a  + (\overrightarrow { - b} )$ .

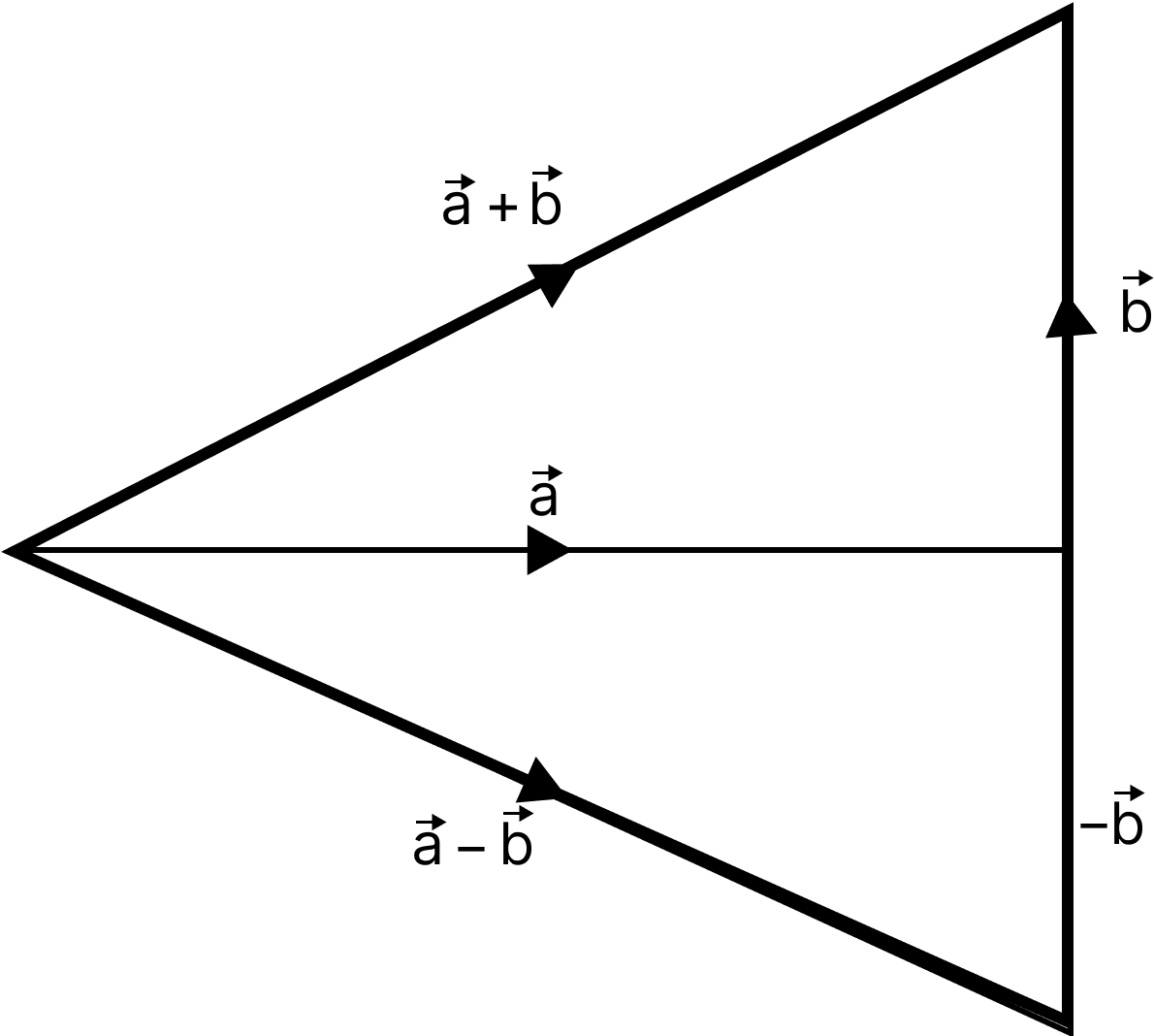
Difference of Vectors

Multiplication of a Vector by a Scalar:

Suppose $\overrightarrow a$ is any vector and m any scalar. Then the multiplication of $\overrightarrow a$ by m is defined as a vector having magnitude |m||$\overrightarrow a$ |and direction same as of $\overrightarrow a$ if m is positive and reversed if m is negative. The product of $\overrightarrow a$  and m is denoted by m. $\overrightarrow a$. If m=0, then m $\overrightarrow a$  is the zero vector.

For example if $\overrightarrow a  = \overrightarrow {AB}$ then $|2\overrightarrow a | = |2||\overrightarrow a | = 2|\overrightarrow a |$ and direction same as that of $\overrightarrow a$ .

The magnitude of the vector $| - 3\overrightarrow a | =  - 3|\overrightarrow a |$ and direction opposite as that of $\overrightarrow a$ .

Important Properties and Formulas:

• Triangle law of vector addition $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$ .

• Parallelogram law of vector addition: if ABCD is a parallelogram, then $\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}$.

• $\overrightarrow a$ and $\overrightarrow b$ are parallel if and only $\overrightarrow a  = m\overrightarrow b$ for some non-zero scalar m.

• $\hat a = \dfrac{{\overrightarrow a }}{{|\overrightarrow {a|} }}$ 

•  $\overrightarrow a  = |\overrightarrow a |\hat a$ 

• Associate law: $m\left( {n\overrightarrow a } \right) = \left( {mn} \right)\overrightarrow a  = n\left( {m\overrightarrow a } \right)$ 

• Distributive laws: $\left( {m + n} \right)\overrightarrow a  = m\overrightarrow a  + n\overrightarrow a$ and $n\left( {\overrightarrow a  + \overrightarrow b } \right) = n\overrightarrow a  + n\overrightarrow b$ 

• If $\overrightarrow r  = x\hat i + y\hat j + z\hat k$ then $m\overrightarrow r  = mx\hat i + my\hat j + mz\hat k$ 

$\overrightarrow r ,\overrightarrow a ,\overrightarrow b$ are coplanar if and only if $\overrightarrow r  = x\overrightarrow a  + y\overrightarrow b$ for some scalar x and y

• If the position vectors of the points A and B  be $\overrightarrow a$ and $\overrightarrow b$ then, the position vectors of the points dividing the line AB in the ratio m:n internally and externally are $\dfrac{{m\overrightarrow b  + n\overrightarrow a }}{{m + n}}$ and $\dfrac{{m\overrightarrow b  - n\overrightarrow a }}{{m - n}}$ 

• Position vector of the middle point of AB is given by $\dfrac{1}{2}\left( {\overrightarrow a  + \overrightarrow b } \right)$ 

• If $\hat r = x\hat i + y\hat j + z\hat k$ then $|\hat r| = \sqrt {{x^2} + {y^2} + {z^2}}$ 

• The points A,B,C will be collinear if and if $\overrightarrow {AB}  = m\overrightarrow {AC}$, for some non-zero scalar m.

Methods to Prove Four Points to be Coplanar:

To prove that the four points A, B, C and D are coplanar. Find the vector $\overrightarrow {AB}, {AC}$ and $\overrightarrow {AD}$  and then prove them to be coplanar by the method coplanar. One of them is a linear combination of the other two.

$|\overrightarrow a  + \overrightarrow b | \leqslant |\overrightarrow a | + |\overrightarrow b |$ 

$|\overrightarrow a  + \overrightarrow b | \geqslant |\overrightarrow a | - |\overrightarrow b |$  

$|\overrightarrow a  - \overrightarrow b | \leqslant |\overrightarrow a | + |\overrightarrow b |$ 

$|\overrightarrow a  - \overrightarrow b | \geqslant |\overrightarrow a | - |\overrightarrow b |$ 

Scalar Product or Dot Product:

The scalar product of two vectors $\overrightarrow a$ and $\overrightarrow b$ is given by 

$\overrightarrow a .\overrightarrow b  = |\overrightarrow a ||\overrightarrow b |\cos \theta$                      $\left( {0 \leqslant \theta  \leqslant \pi } \right)$ 

Where $\theta$ is the angle between $\overrightarrow a \& \overrightarrow b$ 

Projection of $\overrightarrow b$ along $\overrightarrow a$ =$\dfrac{{\overrightarrow b .\overrightarrow a }}{{|\overrightarrow a |}}$ 

Vector or Cross Product:

The vector product of two vectors $\overrightarrow a$ and$\overrightarrow b$ is given by $\overrightarrow a  \times \overrightarrow b  = |A||B| \sin \theta \times \vec{n}$ , where $\theta$ is the angle between $\overrightarrow a \& \overrightarrow b ,\hat n$ is the unit vector perpendicular to $\overrightarrow a \& \overrightarrow b$ .

• The vector perpendicular to both $\overrightarrow a$ and $\overrightarrow b$ is given by $\overrightarrow a  \times \overrightarrow b$ 

• The unit vector perpendicular to both $\overrightarrow a$ and $\overrightarrow b$ is given by $\hat n = \dfrac{{\left( {\overrightarrow a  \times \overrightarrow b } \right)}}{{|\overrightarrow a  \times \overrightarrow b |}}$

Properties of Vector Product:

•  $\overrightarrow a  \times \overrightarrow b  =  - \overrightarrow b  \times \overrightarrow a$ (that is $\overrightarrow a  \times \overrightarrow b  \ne \overrightarrow b  \times \overrightarrow a$ )

• ${\left( {\overrightarrow a  \times \overrightarrow b } \right)^2} = {a^2}{b^2} - {\left( {\overrightarrow a .\overrightarrow b } \right)^2}$

• $\overrightarrow a   = {a_1}\hat i + {a_2}\hat j + {a_3}\hat k ~\& ~\overrightarrow b  = {b_1}\hat i + {b_2}\hat j + {b_3}\hat k$ then $\overrightarrow a  \times \overrightarrow b =\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\a_{1} & a_{2} & a_{3} \\b_{1} & b_{2} & b_{3}\end{array}\right|$ 

• The vector perpendicular to both a and b is given by $\overrightarrow a  \times \overrightarrow b$ 

• The unit vector perpendicular to the plane of $\overrightarrow a$ and $\overrightarrow b$ is $\dfrac{{\overrightarrow a  \times \overrightarrow b }}{{|\overrightarrow a  \times \overrightarrow b |}}$ and a vector magnitude $\lambda$ Perpendicular to the plane of $\left( {\overrightarrow a \& \overrightarrow b } \right)$ is $\pm \dfrac{{\lambda \left( {\overrightarrow a  \times \overrightarrow b } \right)}}{{|\overrightarrow a \& \overrightarrow b |}}$ 

• If $\overrightarrow a$ and $\overrightarrow b$ are collinear then $\overrightarrow a  \times \overrightarrow b  = 0$ 

• The area of a triangle adjacent sides are $\overrightarrow a \& \overrightarrow b$  is given by $\dfrac{1}{2}|\overrightarrow a  \times \overrightarrow b |$ 

• The area of a parallelogram if adjacent sides are  $\overrightarrow a \& \overrightarrow b$ is given by $|\overrightarrow a  \times \overrightarrow b |$ 

• The area of a parallelogram if diagonals are  $\overrightarrow c \& \overrightarrow d$ is given by $= \dfrac{1}{2}|\overrightarrow c  \times \overrightarrow d |$ 

Scalar Triple Product:

If $\overrightarrow a ,\overrightarrow b$ and $\overrightarrow c$ be there vectors, there$\left( {\overrightarrow a  \times \overrightarrow b } \right).\overrightarrow c$ called the scalar triple product of these three vectors.

$\left[ {abc} \right]$ =volume of the parallelepiped whose conterminous edges are dorm by $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ 

$\left[ {abc} \right]$ =$\left[ {bca} \right] = \left[ {cab} \right]$ but$\left[ {abc} \right] =  - \left[ {acb} \right]$ etc.

A change of two vectors in a scalar triple product changes the sign of the scalar triple product.

If any two of the vectors $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ are equal then $\left[ {abc} \right] = 0$ 

The position of dots and crosses in a scalar triple product can be interchanged.

Hence, $\left( {\overrightarrow a  \times \overrightarrow b } \right).\overrightarrow c  = \overrightarrow {a.} \left( {\overrightarrow b  \times \overrightarrow c } \right)$ 

The value of a scalar triple product is zero if two of its vectors are parallel.

$\left[ {\overrightarrow a \overrightarrow {,b}  + \overrightarrow {d,} \overrightarrow c  + \overrightarrow r } \right] = \left[ {\overrightarrow a \overrightarrow b \overrightarrow c } \right] + \left[ {\overrightarrow a \overrightarrow b \overrightarrow r } \right] + \left[ {\overrightarrow a \overrightarrow d \overrightarrow c } \right] + \left[ {\overrightarrow a \overrightarrow d \overrightarrow r } \right]$ 

Application of Vector in Geometry:

Vector equation of a straight line passing through a point $\overrightarrow a$ and parallel$\overrightarrow b$ is $\overrightarrow r  = \overrightarrow a  + t\overrightarrow b$ where t is an arbitrary constant.

Vector equation of a straight line passing two points$\overrightarrow a$ and$\overrightarrow b$  is$\overrightarrow r  = \overrightarrow a  + t\left( {\overrightarrow b  - \overrightarrow a } \right)$ 

Vector equation of a plane passing through a point$\overrightarrow a$ and parallel to two given vectors$\overrightarrow b$ and $\overrightarrow c$ is  $\overrightarrow r  = \overrightarrow a  + s\overrightarrow b  + t\overrightarrow c$ where t and s are arbitrary constants.

Vector equation of a plane passing through the points$\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ is  $\overrightarrow r  = \left( {1 - s - t} \right)\overrightarrow a  + s\overrightarrow b  + t\overrightarrow c$ .

Vector equation of a plane passing through the point $\overrightarrow a$ and perpendicular to $\overrightarrow n$ is $\overrightarrow r .\overrightarrow n  = \overrightarrow {a.} \overrightarrow n$ 

Example:

If the middle points of sides BC,CA & AB of triangle ABC are respectively D,E,F then position vector of centre of triangle DEF, if position vector of A, B, C are respectively $\hat i + \hat j, \hat j + \hat k, \hat k + \hat i$ is

Solution:

The position vector of points D,E,F are respectively

$\dfrac{\overrightarrow B + \overrightarrow C}{2}, \dfrac{\overrightarrow A + \overrightarrow C}{2}, \dfrac{\overrightarrow A + \overrightarrow B}{2}$

$\dfrac{{\hat i + \hat j}}{2} + \hat k, \hat i + \dfrac{{\hat k + \hat j}}{2}$ and $\dfrac{{\hat i + \hat k}}{2} + \hat j$ 

So position vector of the centre of $\Delta DEF$ 

$= \dfrac{1}{3}\left[ {\dfrac{{\hat i + \hat j}}{2} + \hat k + \hat i + \dfrac{{\hat k + \hat j}}{2} + \dfrac{{\hat i + \hat k}}{2} + \hat j} \right]$ 

$= \dfrac{2}{3}\left[ {\hat i + \hat j + \hat k} \right]$ 

Example:

ABCDEF is a regular hexagon with point $\mathrm{O}$  as centre. The value of $\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}+\overrightarrow{A E}+\overrightarrow{A F}$ is $k\overrightarrow{A O}$. What will be the value of k?

Solution:

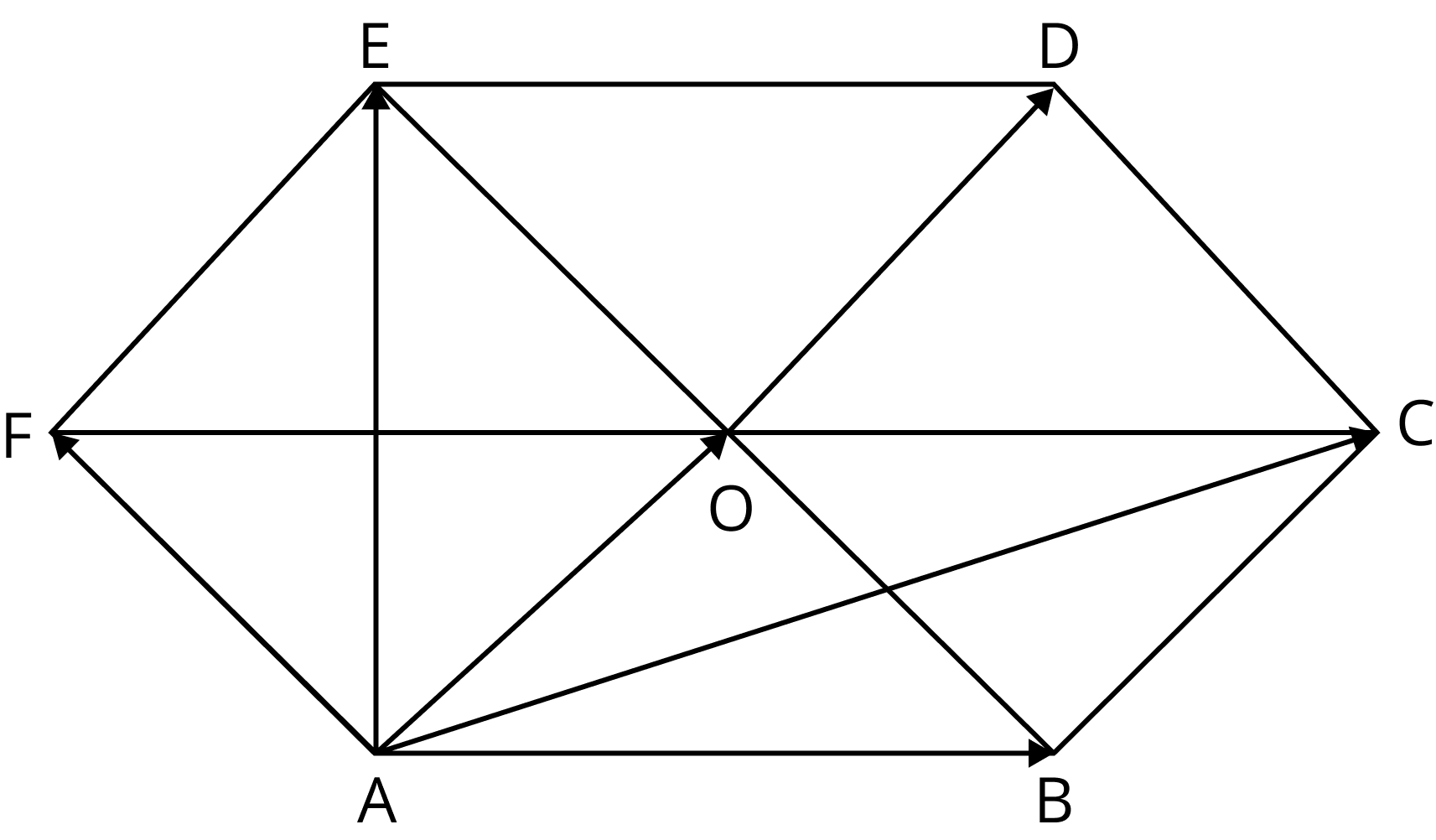
Addition of Vectors

Since, from the figure it can be seen that $\overrightarrow{A B}+\overrightarrow{A F}=\overrightarrow{A O}$

From this, $\overrightarrow{A B}$ can be written as

$\Rightarrow \overrightarrow{A B}=\overrightarrow{A O}-\overrightarrow{A F}$

Also, 

$\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{A O}$

$\overrightarrow{A D}=2 \overrightarrow{A O}$

So by using the above two relation, we can write

$\overrightarrow{A E}=\overrightarrow{A O}+\overrightarrow{A F}$

Now, from the question, it is given that

$\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}+\overrightarrow{A E}+\overrightarrow{A F}=\overrightarrow{k}$

Therefore on substituting the terms, we get

$=5 \overrightarrow{A O}+\overrightarrow{A B}+\overrightarrow{A F}=5 \overrightarrow{A O}+\overrightarrow{A O}=6 \overrightarrow{A O}$

Therefore the value of $\overrightarrow{k}= 6\overrightarrow{A O}$

Common Mistakes/Errors to Avoid:

• Vectors in the same direction can be added by simply adding their magnitudes. But if the vectors to be added are in opposite directions, then their magnitudes are subtracted and not added.

• When two vectors are parallel, their cross product is zero and the dot product is equal to 1.

• There is always linear dependence between two collinear vectors.

• A pair of non-zero, non-collinear vectors are always linearly independent.

• Three coplanar vectors always rely linearly on one another.

• It is always linearly independent for three non-coplanar non-zero vectors.

• The linear dependence of more than three vectors is constant.

• If three vectors are coplanar, then they are linearly dependent on one another, with each one of them being able to be expressed as a linear combination of the other two.

Importance of Vectors - JEE Advanced

This chapter introduces the concept of physical quantities that have both direction and magnitude. The mathematical operations on such quantities will be entirely different from what we have studied in the conventional methods. We have to consider determining the length and magnitude of vectors for ease of calculation.

In this chapter, you will learn what a unit vector is and how it is expressed using particular signs and letters. You will also find out how to define and describe vector components in 2D and 3D spaces. Learn how to find out the components to ease your mathematical calculations.

You will also be introduced to the negative of vectors and explained how to represent it in different aspects. This chapter is important as it creates a strong foundation for a few maths and Physics chapters. This conceptual chapter will also become the base of core subjects taught in the engineering courses. Studying and preparing this chapter at an advanced level will need the assistance of Vectors IIT JEE notes PDF.

Benefits of Vedantu’s Vectors IIT JEE Notes

• These revision notes have been prepared by the subject matter experts. You will find out how all the technical terms have been simplified and explained by the experts in these notes. Learn the basic and advanced formulae of vectors from these notes at ease.

• Find out how the experts have concisely organised all the mathematical principles of this chapter for your convenience. Find out how less time it takes to complete preparing this chapter using these notes.

• Refer to these notes when you revise them. Reduce the time to revise this chapter using these notes and recall what you have studied faster. The format of these notes has made it easier to comprehend and remember all the concepts, formulas, examples, and derivations.

• Learn how to represent the different terms used in this chapter. Find out how these terms and formulae are derived by the experts and use this knowledge for solving problems related to vectors in a better way.

Download Free Vectors Maths IIT JEE Notes PDF

You can download the free PDF version of these notes and complete studying this chapter. Your revision sessions will become more effective and efficient with these revision notes. You can reduce your time to prepare and revise this chapter by using a concise format of this chapter. Solve the sample questions given in the Vectors Maths IIT JEE notes PDF to check your preparation level. Discover the sections you need to study more at your convenience.

Important Related Links for JEE Main and JEE Advanced