NCERT Solutions for Class 12 Chemistry Chapter 2- Electrochemistry

Intext Questions

1. How would you determine the standard electrode potential of the system ${\text{M}}{{\text{g}}^{2 + }}{\text{|Mg}}?$

Ans. A cell with ${\text{Mg}}/{\text{MgS}}{{\text{O}}_4}(1{\text{M}})$ as one electrode and standard hydrogen electrode ${\text{Pt}},{\text{H}},(1\;{\text{atm}}){{\text{H}}^ + }(1{\text{M}})$ as the second electrode will be set up, and the emf of the cell will be measured along with the direction of deflection in the voltmeter. The direction of deflection indicates that ${{\text{e}}^ - }$ move from the magnesium electrode to the hydrogen electrode, implying that oxidation occurs on the magnesium electrode and reduction occurs on the hydrogen electrode. As a result, the cell can be represented in the following way:

$\mathrm{Mg}\left|\mathrm{Mg}^{2+}(1 \mathrm{M}) \| \mathrm{H}^{+}(1 \mathrm{M})\right| \mathrm{H}^{2},(1 \mathrm{~atm}) \mathrm{Pt}$

$E_{\text {cell }}^{o}=E_{H{+} \frac{1}{2}}^{o}-E^{o} \mathrm{Mg}^{2+} / \mathrm{Mg}$

$\text { put } E_{H+\frac{1}{2} H_{2}}^{o}=0$

$\therefore E_{\mathrm{Mg}^{2+} / \mathrm{Mg}}^{o}=-E^{o}{ }_{\text {cell }}$

2. Can you store copper sulphate solutions in a zinc pot?

Ans. ${\text{Cu}}$ is less reactive than ${\text{Zn}}$, so ${\text{Cu}}$ is easily shifted from ${\text{CuS}}{{\text{O}}_4}$solution in the following reaction: 

$\left. {{\text{Zn}}({\text{s}}) + {\text{CuS}}{{\text{O}}_4}({\text{aq}}) \to {\text{ZnSO}}{4_{({\text{q}}q}}} \right) + {\text{Cu}}({\text{s}})$

If we express it in relations of emf, it will be like: 

$\text { Ecell }^{\circ}=\mathrm{Ecu}^{2+} / \mathrm{Cu}^{\circ}-\mathrm{E}^{\circ} \mathrm{zn}^{2+} / \mathrm{Zn}$

$= 0.34\;{\text{V}} - ( - 0.76\;{\text{V}}) = 1.10\;{\text{V}}$

 As, The positive ${\text{E}}_{{\text{cell }}}^{\text{^\circ }}$value indicates the occurrence of spontaneous reactions. if ${\text{CuS}}{{\text{O}}_4}$ is stored in ${\text{Zn}}$ pot, ${\text{Zn}}$ will react will ${\text{Cu}}$ and originality of ${\text{CuS}}{{\text{O}}_4}$ will not be maintained.

3. Consult the table of standard electrode potentials and suggest three substances that can oxidize ferrous ions under suitable conditions.

Ans. In the process of oxidation of ${\text{F}}{{\text{e}}^{2 + }}$ to ${\text{F}}{{\text{e}}^{3 + }}$, i.e., ${\text{F}}{{\text{e}}^{2 + }} \to {\text{F}}{{\text{e}}^{3 + }} + {{\text{e}}^ - };$the reduction potential value is negative in nature i.e. ${{\text{E}}^{\text{o}}}\text{ox}=\text{ }\!\!~\!\!\text{ }-0.77\ \text{V}$. Only compounds with powerful oxidizing agents and positive reduction potentials larger than $0.77\;{\text{V}}$ may oxidize ${\text{F}}{{\text{e}}^{2 + }}$ to ${\text{F}}{{\text{e}}^{3 + }}$, resulting in a positive emf of the cell reaction. This is true for elements like halogens  ${\text{B}}{{\text{r}}_2},{\text{C}}{{\text{l}}_2}$ and ${{\text{F}}_2}$ in the series below ${\text{F}}{{\text{e}}^{3 + }}/{\text{F}}{{\text{e}}^{2 + }}$.

4. Calculate the potential of hydrogen electrode in contact with a solution whose ${\text{pH}}$ is 10.

Ans. For hydrogen electrode, ${{\text{H}}^ + } + {{\text{e}}^ - } \to 1/2{{\text{H}}_2}$

Given: ${\text{pH = 10}}$

Using Nernst equation,

$E_{H^{-} \frac{1}{2} H_{2}}=E_{H^{+} \frac{1}{2} H_{2}}^{o}-\frac{0.0591}{n} \log \frac{1}{\left[H^{+}\right]}$

$0 - \dfrac{{0.0591}}{1}\log \dfrac{1}{{{{10}^{ - 10}}}}$

${{\text{pH  =  10}}}$

${\text{  = -  0}}{\text{0519}} \times {\text{10}}$

$= 0.591{\text{V}}$

Hence, the potential of hydrogen electrode in contact with a solution whose ${\text{pH}}$ is 10 is $0.591\;{\text{V}}$.

5. Calculate the emf of the cell in which the following reaction takes place: ${\text{N}}{{\text{i}}_{({\text{a}})}} + 2{\text{A}}{{\text{g}}^ + }(0.002{\text{M}})$ $ \to {\text{N}}{{\text{i}}^{\text{i}}}^ + (0.160{\text{M}}) + 2{\text{A}}{{\text{g}}_{({\text{a}})}}$ Given that $=\text{E}{}^\circ (\text{coll})1.05\ \text{V}$.

Ans.Using Nernst equation,

${{\text{E}}_{{\text{cell}}}}{\text{ = E}}_{{\text{cell}}}^{\text{o}}{\text{ - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{n}}}{\text{log}}\dfrac{{\left[ {{\text{N}}{{\text{i}}^{{\text{2 + }}}}} \right]}}{{{{\left[ {{\text{A}}{{\text{g}}^{\text{ + }}}} \right]}^{\text{2}}}}}$

$= 1.05\;{\text{V}} - \dfrac{{0.0519}}{2}\log \dfrac{{0.160}}{{{{(0.002)}^2}}}$

$= 1.05 - \dfrac{{0.0591}}{2}\log \left( {\log 4 \times {{10}^4}} \right)$

$= 1.05 - \dfrac{{0.0591}}{2}(4.6021)$

$= 1.05 - 0.14\;{\text{V}} = 0.91\;{\text{V}}$

Therefore, the emf of the cell is $0.91\;{\text{V}}$. 

6.  $0.236\;{\text{V}}$ at $298\;{\text{K}}$. calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.

Ans. $2{\text{F}}{{\text{e}}^3} + ({\text{zg}}) + 2{{\text{I}}^ - }({\text{zq}}) \to 2{\text{F}}{{\text{e}}^2} + ({\text{zg}}) + {{\text{I}}_2}(\;{\text{g}})$

For the given cell, the number of transacted electrons i.e. ${\text{n}} = 2$ 

Using the given formula;

$\Delta_{r} G^{o}=-F E^{o}{ }_{c e l l}$

$=-2 \times 96500 \times 0.236$

$=-45.55 \mathrm{~kJ} \mathrm{~mol}-1$

Also, $\Delta_{r} \mathrm{G}^{\circ}=-2.303 \mathrm{RT} \log \mathrm{KC}$

$\Rightarrow \log K_{c}=\frac{\Delta, G^{o}}{2.303 R T}=\frac{-45.55}{2.303\times 8.314 \times 10^{-3} \times 298}=7.983$

$\Rightarrow K_{c}=\operatorname{antilog}(7.983)$

$=9.616 \times 10^{7}$

7. Why does the conductivity of solution decrease with dilution?

Ans. The conductance of ions contained in a unit volume of solution is called conductivity. The number of ions per unit volume decreases with increase in dilution. As a result, the conductivity drops.

8. Suggest a way to determine the value $\Lambda {}^\circ $of water.

Ans. By using Kohlrausch's law for ${{\text{H}}_2}{\text{O}}$, we can calculate $\Lambda \text{m}{}^\circ$ 

The Kohlrausch Law says that when dissociation is complete at infinite dilution, each ion adds a definite amount to the electrolyte's equivalent conductance, regardless of the nature of the ion with which it is involved, and the value of equivalent conductance at infinite dilution for any electrolyte is the sum of contributions of its ionic species (cations and anions).

$\Lambda \text{m}{}^\circ \text{ }\!\!~\!\!\text{ }=\Lambda \text{m}{}^\circ (\text{Hcl})+\Lambda \text{m}{}^\circ (\text{NaOH})-\Lambda \text{m}{}^\circ (\text{NaCl})$

The  $\Lambda {}^\circ$ values of ${\text{HCl}},{\text{NaOH}}$ and ${\text{NaCl}}$ are known as they are strong electrolytes and dissociates completely.. By putting their values in the above equation, we can have value of  $\Lambda {\text{m}}^\circ $ for ${{\text{H}}_2}{\text{O}}$.

9. The molar conductivity of $0.025 \mathrm{~mol} \mathrm{~L}^{-1}$ methanoic acid is $46.1 \mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1} .$ Calculate its degree of dissociation and dissociation constant Given $\lambda^{0}\left(H^{+}\right)=$ $349.6 \mathrm{~cm}^{2}$ and $\lambda^{\circ}\left(\mathrm{HCOO}^{-}\right)=54.6 \mathrm{~cm}^{2} \mathrm{~mol}^{-1}$

Ans. $\Lambda_{m}^{o}(H C O O H) \lambda^{\circ}\left(H^{+}\right)+\lambda^{\circ}(H C O O)^{-}$

$=349.6+54.6$

$=404.2 \mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1}$

$\Lambda_{m}^{c}=46.1 \mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1}$

$\therefore \alpha= \frac{\Lambda_{m}^{c}}{\Lambda_{m}^{c}}=\frac{46.1}{404.2}=0.114$

10. If a current of $0.5$ampere flows through a metallic wire for 2 hours, then how many electrons would flow through the wire?

Ans. As from the formula, 

$\mathrm{Q}=\mathrm{It}$

$=0.5 \times(2 \times 60 \times 60)=3600 \mathrm{C}$

$1 \mathrm{~F} \Rightarrow 96500 \mathrm{C} \Rightarrow 1 \mathrm{~mole} \text { of } \mathrm{e}^{-1} \mathrm{~s}$

$\therefore 6.02 \times 10^{23} \mathrm{e}^{-1} \mathrm{~s}$

$\therefore 3600 \mathrm{C}$ is equivalent to the flow of $\mathrm{e}^{-1} \mathrm{~s}$

$=\frac{6.02 \times 10^{23}}{96500} \times 3600=2.246 \times 10^{22} e^{-1} s$

11. Suggest a list of metals that are extracted electrolytically.

Ans. ${\text{Na}},{\text{Ca}},{\text{Mg}}$, and ${\text{Al}}$

12. Consider the reaction: ${\text{CrO}}_7^{2 - } + 14{{\text{H}}^ + } + 6{{\text{e}}^ - } \to 2{\text{C}}{{\text{r}}^{3 + }} + 7{{\text{H}}_2}{\text{O}}$. What is the quantity of electricity in coulombs needed to reduce $1\;{\text{mol}}$ of ${\text{C}}{{\text{r}}_2}{\text{O}}_7^{2 - }$

Ans. For the above reaction to take place, $1\;{\text{mol}}$ of ${\text{C}}{{\text{r}}_2}{\text{O}}_7^{2 - }$ will require $6\;{\text{F}}$ $ = 6 \times 96500 = 579000{\text{C}}$0f electricity.

Hence,$579000{\text{C}}$ of electricity are required for reduction of ${\text{C}}{{\text{r}}_2}{\text{O}}_7^{2 - }$ to ${\text{C}}{{\text{r}}^{3 + }}$

13. Write the chemistry of recharging the lead storage battery, highlighting all the materials that are involved during recharging.

Ans. A lead storage battery has a lead anode, a lead cathode with lead dioxide packed$\left( {{\text{Pb}}{{\text{O}}_2}} \right)$ in it, and a $38\% {{\text{H}}_2}{\text{S}}{{\text{O}}_4}$solution as the electrolyte. When the battery is in operation, the following reactions occur:

At Anode: ${\text{P}}{{\text{b}}_{(s)}} + {\text{SO}}_4^{2 - } \to {\text{PbS}}{{\text{O}}_{4(s)}} + 2{e^ - }$

At cathode:${\text{ Pb}}{{\text{O}}_{{\text{2(s)}}}}{\text{  +  S}}{{\text{O}}_{\text{4}}}{^{{\text{2 - }}}_{{\text{(ag)}}}}{\text{  +  4}}{{\text{H}}^{\text{ + }}}_{{\text{(aq)}}}{\text{  +  2}}{{\text{e}}^ - }\xrightarrow{{}}{\text{PbS}}{{\text{O}}_{{\text{4(s)}}}}{\text{ +  2}}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\text{(l)}}}}$

Complete reaction: $P{b_{(s)}} + Pb{O_{2(s)}} + 2{H_2}S{O_{4(aq)}} \to 2PbS{O_{4(s)}} + 2{H_2}{O_{(l)}}$

The reverse process occurs when the battery is charged, in which ${\text{PbS}}{{\text{O}}_{\text{4}}}$ deposited on the electrodes is transformed back to ${\text{Pb}}$and ${\text{Pb}}{{\text{O}}_2}$, and ${{\text{H}}_2}{\text{S}}{{\text{O}}_4}$ is restored.

14. Suggest two materials other than hydrogen that can be used as fuels in fuel cells.

Ans. Methane and Methanol.

15. Explain how rusting of iron is envisaged as setting up of an electro chemical cell

Ans.The Water present on the surface of iron dissolves acidic oxides of air like ${\text{C}}{{\text{O}}_2},{\text{S}}{{\text{O}}_2}$ etc, to form acids which dissociate to give ${{\text{H}}^ + }$ ions:

${{\text{H}}_2}{\text{O}} + {\text{C}}{{\text{O}}_2} \to {{\text{H}}_2}{\text{C}}{{\text{O}}_3} \rightleftharpoons 2{{\text{H}}^ + } + {\text{CO}}_3^{2 - }$

In the presence of ${{\text{H}}^ + }$, iron${\text{F}}{{\text{e}}^{2 + }}$ releases ${{\text{e}}^{ - 1}}$ to form ${\text{F}}{{\text{e}}^{3 + }}$. Hence, this acts as anode:

${\text{F}}{{\text{e}}_{(s)}} \to {\text{F}}{{\text{e}}^{2 + }}_{({\text{aq}})} + 2{{\text{e}}^ - }$

The ${{\text{e}}^{ - 1}}$ lost then travel through the metal to reach place where these electrons are utilized by ${{\text{H}}^ + }$ ions and dissolved oxygen and reduction takes place. Thus acts as cathode:

${{\text{O}}_2}(\;{\text{g}}) + 4{{\text{H}}^ + }_{({\text{aq}})} + 4{{\text{e}}^ - } \to 2{{\text{H}}_2}{{\text{O}}_{({\text{g}})}}$

The overall reaction is:

$2{\text{F}}{{\text{e}}_{({\text{s}})}} + {{\text{O}}_2}_{(\;{\text{g}})} + 4{{\text{H}}^ + }_{({\text{aq}})} \to 2{\text{F}}{{\text{e}}^{2 + }}_{({\text{aq}})} + 2{{\text{H}}_2}{{\text{O}}_{({\text{l}})}}$

As a result, an electrochemical cell is established on the surface. The atmospheric oxygen oxidizes ferrous ions to ferric ions, which mix with water to produce hydrated ferric oxide., ${\text{F}}{{\text{e}}_2}{{\text{O}}_3}.{\text{X}}{{\text{H}}_2}{\text{O}}$ which is known as rust.

Ncert Exercises 

1. Arrange the following metals in the order in which they displace each other from the solution of their salts: ${\text{Al}},{\text{Cu}},{\text{Fe}},{\text{Mg}}$ and ${\text{Zn}}$

 Ans. ${\text{Mg}},{\text{Al}},{\text{Zn}},{\text{Fe}},{\text{Cu}},{\text{Ag}}$

2. Given the standard electrode potentials, ${{\text{K}}^ + }/{\text{K}} = 2.93\;{\text{V}},{\text{A}}{{\text{g}}^ + }/{\text{Ag}} = 0.80\;{\text{V}}$

${\text{H}}{{\text{g}}^{2 + }}/{\text{Hg}} = 0.79\;{\text{V}}$

${\text{M}}{{\text{g}}^{2 + }}/{\text{Mg}} =  - 2.73\;{\text{V}},{\text{C}}{{\text{l}}^{3 + }}/{\text{Cr}} = 0.74\;{\text{V}}$

Arrange these metals in their increasing order of reducing power.

Ans: The larger the oxidation potential, the easier it is to oxidize it, and hence the higher the reducing power. As a result, the reducing power of the elements will be in the following ascending sequence: ${\text{Ag}} < {\text{Hg}} < {\text{Cl}} < {\text{Mg}} < {\text{K}}$.

3. Depict the galvanic cell in which the reaction, $2\text{A}{{\text{g}}^{\text{ + }}}\ \left( \text{aq} \right)\ \xrightarrow{{}}\text{Z}{{\text{n}}^{\text{2 + }}}\left( \text{aq} \right)\text{ + 2Ag(s)}$takes place. Further show:

Ans.  The set-up will be similar to the one seen below.

(i) Which of the electrode is negatively charged?

Ans. The anode, or zinc electrode, will have a negative charge.

(ii) The carriers of the current in the cell.

Ans. In the external circuit, current will travel from silver to copper.

(iii) Individual reaction at each electrode.

Ans. At anode: ${\text{Zn}}\left( {({\text{n}}) \to {\text{Z}}{{\text{n}}^{2 + }}({\text{q}}) + 2{{\text{e}}^ - }} \right.$

At cathode: $2{\text{A}}{{\text{g}}^ + }_{({\text{zq}})} + 2{{\text{e}}^ - } \to 2{\text{A}}{{\text{g}}_{({\text{i}})}}$

4. Calculate the standard cell potentials of galvanic cell in which the following reactions take place

(i) $2 \mathrm{Cr}(\mathrm{s})+\mathrm{Cd}^{2+}_{(a q)} \rightarrow 2 \mathrm{Cr}^{3+}{ }_{(a q)}+3 \mathrm{Cd}_{(s)}$

(ii) $\mathrm{Fe}^{2+}_{(a q)}+\mathrm{Ag}_{(a q)}^{+} \rightarrow \mathrm{Fe}^{3+}_{(a q)}+\operatorname{Ag}(s)$

Calculate the $\Delta_{r} G^{o}$ and equilibrium constant of the reactions

Given

$E_{\mathrm{Cr}^{3}, \mathrm{Cr}}^{o}=-0.74 \mathrm{~V}$

$E_{\mathrm{Cr}^{2+}, \mathrm{Cd}}^{o}=-0.40 \mathrm{~V}$

$E_{\mathrm{Ag}^{+}}^{o} A g=0.80 \mathrm{~V}$

$E_{F e^{3},{ }_{F e^{2+}}}^{o}=0.77 \mathrm{~V}$

Ans: $E^{\circ} \text { cell }=E^{\circ} \text { cathode }-E^{\circ} \text { Anode }$

$=-0.40 \mathrm{~V}-(-0.74 \mathrm{~V})=+0.34 \mathrm{~V}$

$\Delta_{r} G^{o}=\mathrm{nFE}^{\circ} \text { cell }$

$=-6 \times 96500 \mathrm{C} \mathrm{mol}^{-1} \times 0.34 \mathrm{~V}$

$=196860 \mathrm{C} \mathrm{V} \mathrm{mol}^{-1}$

$=196860 \mathrm{~J} \mathrm{~mol}^{-1}$

$=-196.86 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$-\Delta_{r} G^{\circ}=2.303 \mathrm{x} 8.314 \times 298 \log \mathrm{K}$

$196860=2.303 \times 8.314 \times 298 \log \mathrm{K}$

$\text { or } \log \mathrm{K}=34.5014$

$\mathrm{~K}=\text {Antilog} 34.5014=3.172 \times 10^{34}$

(ii) $\mathrm{E}^{\circ} \mathrm{cell}=+0.80 \mathrm{~V}-0.77 \mathrm{~V}=+0.03 \mathrm{~V}$

$\Delta_{r} G^{o}=\mathrm{nFE}^{\circ} \text { cell }$

$=-1 \times\left(96500 \mathrm{C} \mathrm{V} \mathrm{mol}^{-1}\right) \times(0.03 \mathrm{~V})$

$=-2.895 \mathrm{C} \mathrm{V} \mathrm{mol}^{-1}=-2895 \mathrm{~J} \mathrm{~mol}^{-1}$

$=2.895 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$\Delta_{r} G^{o}=2.303 \mathrm{RT} \log \mathrm{K}$

$-2895=-2.303 \times 8.314 \times 298 \times \log \mathrm{K}$

or $\log \mathrm{K}=0.5074$

or $\mathrm{K}=\operatorname{Antilog}(0.5074)=3.22$

5. Write the Nernst equation and emf of the following cells at $298\;{\text{K}}$

(i) $\mathrm{Mg}_{(s)} \mid \mathrm{Mg}^{2+}(0.001 \mathrm{M}) \| \mathrm{Cu}^{2+}(0.0001 \mathrm{M}) \mathrm{Cu}_{(\mathrm{s})}$

(ii) $\text{F}{{\text{e}}_{(s)}}\mid \text{F}{{\text{e}}^{2+}}(0.001\text{M})\|{{\text{H}}^{+}}(1\text{M}){{\text{H}}_{2}}(~\text{g})(1\,\text{bar)P}{{\text{t}}_{(\text{S})}}$

(iii) $\text{S}{{\text{n}}_{(\text{s})}}\left| \text{S}{{\text{n}}^{2+}}(0.050\text{M})\|{{\text{H}}^{+}}(0.020\text{M}) \right|{{\text{H}}_{2}}(~\text{g})(1\,\text{bar)P}{{\text{t}}_{\text{(S)}}}$

(iv) $\text{P}{{\text{t}}_{(\text{s})}}\left| \text{B}{{\text{r}}_{2(\text{I})}} \right|\text{Br}-(0.010\text{M})\|\text{H}+(0.030\text{M}){{\text{H}}_{2(~\text{g})}}(1\,\text{bar)P}{{\text{t}}_{(\text{S})}}$

Given ${\text{E}}^\circ {\text{CellM}}{{\text{g}}^{2 + }},{\text{Mg}} = - 2.37\;{\text{V}}$,

\[{\text{E}}^\circ {\text{c}}{{\text{u}}^{2 + }},{\text{Cu}} = + 0.34\;{\text{V}},{\text{E}}^\circ {\text{F}}{{\text{e}}^{2 + }}{\text{Fe}} = - 0.44\;{\text{V}}\]

${\text{E}}^\circ {\text{S}}{{\text{n}}^{2 + }}/{\text{Sn}} = - 0.14\;{\text{V}}$

\[{\text{E}}^\circ 1/2{\text{B}}{{\text{r}}_2}/{\text{B}}{{\text{r}}^ - } = + 1.08\;{\text{V}}\]

(i) 

Ans. Cell reaction:

${\text{Mg}} + {\text{C}}{{\text{u}}^{2 + }} \to {\text{M}}{{\text{g}}^{2 + }} + {\text{Cu}}({\text{n}} = 2)$

Applying Nernst equation:

${{\text{E}}_{{\text{cell }}}}{\text{ = E}}_{{\text{Cell }}}^{\text{^\circ }}{\text{ - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{\left[ {{\text{M}}{{\text{g}}^{{\text{2 + }}}}} \right]}}{{\left[ {{\text{C}}{{\text{u}}^{{\text{2 + }}}}} \right]}}$

${{\text{E}}_{{\text{cell }}}}{\text{ = 0}}{\text{.34 - ( - 2}}{\text{.37) - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{{\text{1}}{{\text{0}}^{{\text{ - 3}}}}}}{{{\text{1}}{{\text{0}}^{{\text{ - 4}}}}}}$

$= 2.71 - 0.02955 = 2.68\;{\text{V}}$

(ii) 

Ans. Cell reaction:

${\text{Fe}} + 2{{\text{H}}^ + } \to {\text{F}}{{\text{e}}^{2 + }} + {{\text{H}}_2}({\text{n}} = 2)$

Applying Nernst equation  

${{\text{E}}_{{\text{cell }}}}{\text{ = E}}_{{\text{cell }}}^{\text{o}}{\text{ - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{\left[ {{\text{F}}{{\text{e}}^{{\text{2 + }}}}} \right]}}{{{{\left[ {{{\text{H}}^{\text{ + }}}} \right]}^{\text{2}}}}}$

${{\text{E}}_{{\text{cell }}}}{\text{ = 0 - ( - 0}}{\text{.44) - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{{\text{1}}{{\text{0}}^{{\text{ - 3}}}}}}{{{{{\text{(1)}}}^{\text{2}}}}}$

$= 0.44 - \dfrac{{0.0591}}{2} \times ( - 3)$

$= 0.44 + 0.0887 = 0.5287\;{\text{V}}$

(iii) 

Ans. Cell reaction:

${\text{Sn}} + 2{{\text{H}}^ + } \to {\text{S}}{{\text{n}}^{2 + }} + {{\text{H}}_2}({\text{n}} = 2)$

Applying Nernst equation:

${{\text{E}}_{{\text{cell}}}}{\text{ = E}}_{{\text{cell}}}^{\text{^\circ }}{\text{ - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{\left[ {{\text{s}}{{\text{n}}^{{\text{2 + }}}}} \right]}}{{{{\left[ {{{\text{H}}^{\text{ + }}}} \right]}^{\text{2}}}}}$

${{\text{E}}_{{\text{cell}}}}{\text{ = E}}_{{\text{cell}}}^{\text{^\circ }}{\text{ - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{{\text{0}}{\text{.05}}}}{{{{{\text{(0}}{\text{.02)}}}^{\text{2}}}}}$

$= 0 - ( - 0.14) - \dfrac{{0.0591}}{2}\log \dfrac{{0.05}}{{{{(0.02)}^2}}}$

$= 0.14 - \dfrac{{0.0591}}{2}\log 125$

$= 0.14 - \dfrac{{0.0591}}{2}(2.0969) = 0.078\;{\text{V}}$

(iv)

Ans. Cell reaction:

$2{\text{Br}} + 2{{\text{H}}^ + } \to {\text{B}}{{\text{r}}_2} + {{\text{H}}_2}({\text{n}} = 2)$

Applying Nernst equation:

${{\text{E}}_{{\text{cell}}}}{\text{ = E}}_{{\text{cell}}}^{\text{^\circ }}{\text{ - }}\dfrac{{{\text{0}}{\text{.0591}}}}{{\text{2}}}{\text{log}}\dfrac{{\text{1}}}{{{{\left[ {{\text{B}}{{\text{r}}^{\text{ - }}}} \right]}^{\text{2}}}{{\left[ {{{\text{H}}^{\text{ + }}}} \right]}^{\text{2}}}}}$

$= (0 - 1.08) - \dfrac{{0.0591}}{2}\log \dfrac{1}{{{{(0.01)}^2}{{(0.03)}^2}}}$

$=  - 1.08 - \dfrac{{0.0591}}{2}\log \left( {1.111 \times {{10}^7}} \right)$

$=  - 1.08 - \dfrac{{0.0591}}{2}(7.0457)$

$=  - 1.08 - 0.208 =  - 1.288\;{\text{V}}$

As a result, oxidation will take place at the hydrogen electrode, whereas reduction will take place at the ${\text{B}}{{\text{r}}_2}$ electrode.

6. In the button cells widely used in watches and other devices the following reaction takes places:

Determine $\Delta \text{rG}{}^\circ $ and $\text{E}{}^\circ $ for the reaction.

Given \[\text{Zn}\to \text{Z}{{\text{n}}^{2+}}+2{{\text{e}}^{-}},\text{E}{}^\circ =0.76\ \text{V}\]

\[\text{A}{{\text{g}}_{2}}\text{O}+{{\text{H}}_{2}}\text{O}+2{{\text{e}}^{-}}\to 2\text{Ag}+2\text{O}{{\text{H}}^{-}},\text{E}{}^\circ =0.344\text{v}\]

Ans. In the given reaction, ${\text{Zn}}$is getting oxidized and ${\text{A}}{{\text{g}}_2}{\text{O}}$ is being reduced.

$\text{E}{}^\circ \text{cell}$$= 0.344 + 0.76 = 1.104\;{\text{V}}$

$\Delta \text{G}{}^\circ =\text{nFE}{}^\circ \text{cell}=\text{ }\!\!~\!\!\text{ }-2\times 96500\times 1.104\ \text{J}$

$\Delta \text{G}{}^\circ $$=  - 2.13 \times {10^5}\;{\text{J}}$

7. Define conductivity and molar conductivity for the solution of an electrolyte. Discuss their variation with concentration.

Ans. The conductivity of a solution is defined as the conductance of a solution with a length of 1${\text{cm}}$and a cross-sectional area of 1 s${\text{cm}}$. 

When the electrodes are one cm apart and the area of cross-section of the electrodes is large enough that the entire solution is contained between them, the molar conductivity of a solution at a dilution$({\text{V}})$ is the conductance of all the ions produced from one mole of the electrolyte dissolved in the solution${\text{Vc}}{{\text{m}}^3}$. ${\Lambda _m}$ is the most common symbol for conductivity.

The conductivity of a solution (for both strong and weak electrolytes) diminishes as the concentration of the electrolyte drops, i.e. as dilution occurs. This is owing to the fact that when the solution is diluted, the number of ions per unit volume of the solution decreases.

On dilution, the molar conductivity of a solution increases as with decrease in concentration of the electrolyte. This is owing to the fact that when the solution is diluted, the number of ions per unit volume of the solution decreases. The molar conductivity of a solution increases as the electrolyte content drops. This is because dilution increases both the quantity of ions and their mobility. The molar conductivity is known as limiting molar conductivity as the concentration approaches zero.

8. The conductivity of $0.20{\text{M}}$ solution of ${\text{KCl}}$ at $298\;{\text{K}}$ is $0.0248\;{\text{S}}\;{\text{c}}{{\text{m}}^{ - 1}}.$ Calculate its molar conductivity.

Ans. ${\Lambda _{\text{m}}}{\text{ = }}\;\dfrac{{{\text{k}} \times {\text{1000}}}}{{{\text{ Molanity }}}}{\text{ = }}\;\dfrac{{{\text{0}}.{\text{2485}}\;{\text{c}}{{\text{m}}^{\:{\text{ - }}\:{\text{1}}}} \times {\text{1000}}\;{\text{c}}{{\text{m}}^{\text{3}}}{{\text{L}}^{\:{\text{ - }}\:{\text{1}}}}}}{{{\text{0}}{\text{.20mo}}{{\text{L}}^{\:{\text{ - }}\:{\text{1}}}}}} = 124\;{\text{Sc}}{{\text{m}}^2}{\text{mo}}{{\text{l}}^{ - 1}}$

9. The resistance of a conductivity cell containing $0.001{\text{MKCl}}$ solution at $298\;{\text{K}}$ is $1500\Omega $. What is the cell constant if conductivity of $0.001{\text{MKCl}}$ solution at $298\;{\text{K}}$ is $0.146 \times {10^{ - 3}}\;{\text{S}}\;{\text{c}}{{\text{m}}^{ - 1}}?$

Ans. From the following relation:

$\;\;{\text{Cell constant}} = \dfrac{{{\text{ Conductivity }}}}{{{\text{ Conductance }}}} = {\text{ Conductivity }} \times {\text{Resistance}}\;\;$

 $= 0.146 \times{10^{ - 3}}\;{\text{S}}\;{\text{c}}{{\text{m}}^{ - 1}} \times 1500\Omega$

$=0.218\;{\text{c}}{{\text{m}}^{ - 1}}$

10. The conductivity of ${\text{NaCl}}$ at $298\;{\text{K}}$ has been determined at different concentrations and the results are given below:

for all concentrations and draw a plot between ${\Lambda _{\text{m}}}$ and ${{\text{C}}^{1/2}}$

Find the value of ${{\Lambda }_{\text{m}}}{}^\circ$

Ans.

Using the following unit conversion factor, $\dfrac{{1S\;{\text{c}}{{\text{m}}^{ - 1}}}}{{100{\text{S}}{{\text{m}}^{ - 1}}}} = 1$

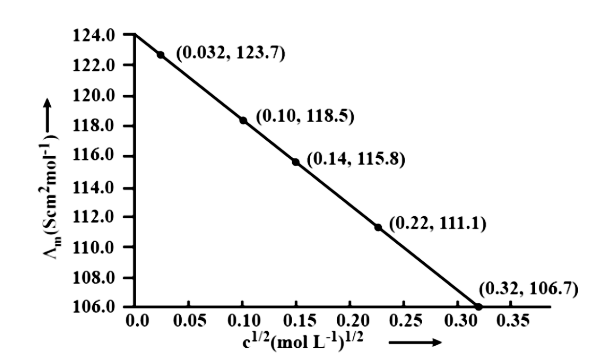
$\Lambda {}^\circ \text{cm}=$ Intercept of $\Lambda {\text{m}}$axis $= 124.0\;{\text{S}}\;{\text{c}}{{\text{m}}^2}\;{\text{mo}}{{\text{l}}^{ - 1}}$, Extrapolation to zero concentration yields this result.

11. Conductivity of $0.00241{\text{M}}$ acetic acid is $7.896 \times {10^{ - 5}}{\text{Sc}}{{\text{m}}^{ - 1}}.$ Calculate its. Calculate its molar conductivity. If $\Lambda {}^\circ \text{m}$ for acetic acid is $390.5\;{\text{S}}\;{\text{c}}{{\text{m}}^2}\;{\text{mo}}{{\text{l}}^{ - 1}}$, what is its dissociation constant?

Ans. $\Lambda _{\text{m}}^{\text{c}}{\text{ = }}\dfrac{{\kappa \times {\text{1000}}}}{{{\text{ Molarity }}}}$

$=\frac{(7.896\times10^{-5}Scm^{-1}\times1000cm^{3}L^{-1})}{0.241\times mol L^{-1}}=32.76 S cm^{2}mol^{-1}$

\[\alpha  = \dfrac{{\Lambda _m^c}}{{\Lambda m^\circ }} = \dfrac{{32.76}}{{390.5}} = 8.4 \times {10^{ - 2}}\]

${k_a} = \dfrac{{C{\alpha ^2}}}{{1 - \alpha }} = \dfrac{{0.24 \times {{\left( {8.4 \times {{10}^{{\text{ }} - 2}}} \right)}^2}}}{{1 - 0.084}} = 1.86 \times {10^{{\text{ }} - 5}}$

12. How much charge is required for the following reductions:

1. $\mathbf{1\;{\text{mol}}}$of $\mathbf{{\text{A}}{{\text{l}}^{3 + }}}$ to $\mathbf{{\text{Al}}}$ ?

 Ans. Aluminum ion have to lose three electrons to be in aluminum elemental state and the reaction is ${\text{A}}{{\text{l}}^{3 + }} + 3{\text{e}} \to {\text{Al}}$. The amount of charge needed for reduction of $1\;{\text{mol}}$ will be: ${\text{A}}{{\text{l}}^{3 + }} = 3\;{\text{F}} = 3 \times 96500{\text{C}} = 289500{\text{C}}$.

2. $\mathbf{1\;{\text{mol}}}$ of $\mathbf{{\text{C}}{{\text{u}}^{2 + }}}$ to $\mathbf{{\text{Cu}}?}$

Ans. cupric ion needs to lose two electrons to be in copper (0) state. The electrode reaction occurring is as follows: ${\text{C}}{{\text{u}}^{2 + }} + 2{{\text{e}}^ - } \to {\text{Cu}}$

The amount of charge required for conversion of $1\;{\text{mol}}$ of ${\text{C}}{{\text{u}}^{2 + }} = 2\;{\text{F}} = 2 \times 96500 = 193000{\text{C}}$.

3. $\mathbf{1\;{\text{mol}}}$ of $\mathbf{{\text{Mn}}{{\text{O}}^4}}$ to $\mathbf{{\text{M}}{{\text{n}}^{2 + }}}$ 

Ans. in the compound ${\text{Mn}}{{\text{O}}^4}$, manganese is in +7 oxidation state; which is reduced to +2 oxidation state with the release of five electrons.

${\text{Mn}}{{\text{O}}_4} \to {\text{M}}{{\text{n}}^{2 + }}$ i.e. ${\text{M}}{{\text{n}}^{7 + }} + 5{{\text{e}}^ - } \to {\text{M}}{{\text{n}}^{2 + }}$

The Quantity of charge needed for reduction of  $1\;{\text{mol}}$ of ${\text{Mn}}{{\text{O}}^4}$ to ${\text{M}}{{\text{n}}^{2 + }}$ $ = 5\;{\text{F}} = 5 \times 96500{\text{C}} = 4825000{\text{C}}$.

13. How much electricity in terms of Faraday is required to produce.

1. $\mathbf{20.0\;{\text{g}}}$ of $\mathbf{{\text{Ca}}}$ a from molten $\mathbf{{\text{CaC}}{{\text{l}}_2}}$ ?

Ans. ${\text{C}}{{\text{a}}^{2 + }} + 2{{\text{e}}^ - } \to {\text{Ca}}$

As There are two electrons transacted in the above reaction, therefore ${\text{1 mol}}$ of ${\text{Ca}}$or $40\;{\text{g}}$ of ${\text{Ca}}$will require $ = 2\;{\text{F}}$ electricity and $20\;{\text{g}}$ of ${\text{Ca}}$will require $ = 1\;{\text{F}}$ of electricity.

2. $\mathbf{40.0\;{\text{g}}}$ of $\mathbf{{\text{Al}}}$ from molten $\mathbf{{\text{A}}{{\text{l}}_2}{{\text{O}}_3}}$ ?

Ans. ${\text{A}}{{\text{l}}^{3 + }} + 3{{\text{e}}^ - } \to {\text{Al}}$

As the number of electrons transacted in the above reduction of aluminum ion is three,

Therefore,  ${\text{1 mol}}$of ${\text{Al}}$ or $27\;{\text{g}}$ of ${\text{Al}}$ will require = $3\;{\text{F}}$ electricity

And,

$40\;{\text{g}}$ of ${\text{Al}}$ will require electricity

${\text{ = }}\dfrac{{\text{3}}}{{{\text{27}}}}{{ \times 40 = 4}}{\text{.44F}}$ of electricity.

14. How much electricity is required in coulomb for the oxidation of

1. $\mathbf{1\;{\text{mol}}}$ of $\mathbf{{{\text{H}}_2}{\text{O}}$ to ${{\text{O}}_2}}$

Ans. The oxidation of water occurs in the following way:

${{\text{H}}_{\text{2}}}{\text{O}}\xrightarrow{{}}{{\text{H}}_{\text{2}}}{\text{ + }}\dfrac{{\text{1}}}{{\text{2}}}{{\text{O}}_{\text{2}}}$

Or

${{\text{O}}^{{\text{2 - }}}}\xrightarrow{{}}\dfrac{{\text{1}}}{{\text{2}}}{{\text{O}}_{\text{2}}}{\text{ + 2}}{{\text{e}}^{\text{ - }}}$

The number of electrons transacting are two. Therefore the amount of electricity needed $ = 2\;{\text{F}} = 2 \times 96500{\text{C}} = 193000{\text{C}}$

2. $\mathbf{1\;{\text{mol}}}$ of $\mathbf{{\text{FeO}}}$ to $\mathbf{{\text{F}}{{\text{e}}_2}{{\text{O}}_3}}$

Ans. The oxidation reaction of ${\text{FeO}}$ takes place in the following manner:

${\text{FeO}} + \dfrac{1}{2}{{\text{O}}_2} \to \dfrac{1}{2}\;{\text{F}}{{\text{e}}_2}{{\text{O}}_3}$

Or

${\text{F}}{{\text{e}}^{2 + }} \to {\text{F}}{{\text{e}}^{3 + }} + {{\text{e}}^ - }$

The electron transfer is of one electron unit, therefore the Quantity of electricity essential $ = 1\;{\text{F}} = 96500{\text{C}}$

15. A solution of $\mathbf{{\text{Ni}}{\left( {{\text{N}}{{\text{O}}_3}} \right)_2}}$ is electrolyzed between platinum electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?

Ans. firstly, we will find charge in coulombs using the formula: ${\text{Q  =  It}}$

Amount of electricity passed${\text{(Q)}}$ $ = (5\;{\text{A}}) \times (20 \times 60{\text{sec}}) = 6000{\text{C}}$

The reduction of nickel occurs in the following way:

${\text{N}}{{\text{i}}^{2 + }} + 2{{\text{e}}^{\text{ - }}}{\text{ }}\xrightarrow{{}}{\text{Ni}}$

Therefore, $2\;{\text{F}}$or $2 \times 96500{\text{C}}$is the amount of charge deposit for \[{\text{1 mol}}\] of ${\text{Ni}} = 58.7\;{\text{g}}$

Now,

The $6000{\text{C}}$ of charge will deposit $ = \dfrac{{58.7 \times 6000}}{{2 \times 96500}} = 1.825\;{\text{g}}$ of ${\text{Ni}}$

16. Three electrolytic cells, $\mathbf{{\text{A}},{\text{B}},{\text{C}}}$ containing solutions of $\mathbf{{\text{ZnS}}{{\text{O}}_4},{\text{AgN}}{{\text{O}}_3}}$ and $\mathbf{{\text{CuS}}{{\text{O}}_4}}$, respectively are connected in series. A steady current of 1.5amperes was passed through them until $\mathbf{45\;{\text{g}}}$ of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and zinc were deposited?

Ans. Given: ${\text{I = 1}}{{.5\;A,\;W = 1}}{{.5\;g}}$ of ${\text{Ag t}} = ?,{\text{E}} = 108,{\text{n}} = 1$

Applying Faraday's first law of electrolysis,

${\text{W}} = {\text{ZIt}}$ 

Or

 ${\text{W = }}\dfrac{{\text{E}}}{{{\text{nF}}}}{\text{It}}$ 

By substituting the values provided in the about formula,${\text{t}}$can be calculated;

 ${\text{t = }}\dfrac{{{\text{1}}{{.45 \times 96500}}}}{{{\text{1}}{{.5 \times 108}}}}{\text{ = 863}}{\text{.73}}$ seconds.

Now for ${\text{Cu}},{{\text{W}}_{\text{1}}} = 1.45\;{\text{g(given)}}$ of ${\text{Ag}}{{\text{E}}_1} = 108,\;{{\text{W}}_2} = ?$

${{\text{E}}_2} = 31.75$

Applying Faraday's ${2^{{\text{nd }}}}$ law of electrolysis

 $\dfrac{{{{\text{W}}_{\text{1}}}}}{{{{\text{W}}_{\text{2}}}}}{\text{ = }}\dfrac{{{{\text{E}}_{\text{1}}}}}{{{{\text{E}}_{\text{2}}}}}$

$\dfrac{{{\text{1}}{\text{.45}}}}{{{{\text{W}}_{\text{2}}}}}{\text{ = }}\dfrac{{{\text{108}}}}{{{\text{31}}{\text{.75}}}}{{\;\;}}$

${{\text{W}}_{\text{2}}}{\text{  =  }}\dfrac{{{\text{1}}.{\text{45}} \times {\text{31}}{\text{.75}}}}{{{\text{108}}}}$

Copper deposited $ = 0.426\;{\text{g}}$ of ${\text{Cu}}$

likewise, 

for ${\text{Zn}},{{\text{W}}_1} = 1.45\;{\text{g}}$ of ${\text{Ag}},{{\text{E}}_1} = 108$,

${\text{W}}2 = ?{\text{E}}2 = 32.65$

Using formula, $\dfrac{{{{\text{W}}_{\text{1}}}}}{{{{\text{W}}_{\text{2}}}}}{\text{ = }}\dfrac{{{{\text{E}}_{\text{1}}}}}{{{{\text{E}}_{\text{2}}}}}$

$\dfrac{{{\text{1}}{\text{.45}}}}{{{{\text{W}}_{\text{2}}}}}{\text{ = }}\dfrac{{{\text{108}}}}{{{\text{32}}{\text{.65}}}}$

${{\text{W}}_{\text{2}}}{\text{ = }}\dfrac{{{\text{1}}{{.45 \times 32}}{\text{.65}}}}{{{\text{108}}}}{\text{ = 0}}{\text{.438}}$ of ${\text{Zn}}$

Zinc deposited by \[{\text{1295}}{\text{.6g C}}\] is 0.438 g.

17. Predict if the reaction between the following is feasible:

Given standard electrode potentials:

$\mathbf{E_{1 / 2, I_{2}, I^{-}}^{o}=+0.451 V}$

$\mathbf{E_{C u^{2+}, C u}^{o}=+0.34 V}$

$\mathbf{E_{1 / 2 B r_{2}, B r^{-}}^{o}=+1.09 V}$

$\mathbf{E_{A g^{+}, A g}^{o}=+0.80 V, E_{F e^{3+}, F e^{2+}}^{o}=+0.77 V}$

1. $\mathrm{Fe}^{3+} \text { (aq) and } \mathrm{I}^{-} \text {(aq) }$

Ans: The reaction is feasible if the emf of the cell reaction is positive.

$\text { (i) } F e^{3+}(a q)+I_{(a q)}^{-} \rightarrow F e^{2+}(a q)+\frac{1}{2} I^{2}(g)$

$\text { i.e., } P t / I^{2} / I^{-}(a q) \| F e^{3+}(a q)\left|F e^{2+}(a q)\right| P t$

$\therefore E_{c e l l}^{o}=E_{F e^{3+} \cdot F e^{2+}}-E^{o}_{1 / 2 I_{2}, f^{2}}$

$=0.77-0.54=0.23 V \text { (Feasibles)}$

2. $\mathbf{2 \mathrm{Ag}^{+}{ }_{(a q)}+C u_{(s)} \rightarrow 2 \mathrm{Ag}_{(s)}+\mathrm{Cu}^{2+}_{(a q)}}$

Ans: $2 \mathrm{Ag}^{+}{ }_{(a q)}+C u_{(s)} \rightarrow 2 \mathrm{Ag}_{(s)}+\mathrm{Cu}^{2+}_{(a q)}$

$\text { i.e., } \mathrm{Cu}\left|\mathrm{Cu}^{2+}{(a q)} \| \mathrm{Ag}_{(a q)}^{+}\right| \mathrm{Ag}$

$\therefore E_{c e l l}^{o}=E^{o}{ }_{A g^{+A g}}-E_{C u}^{o}, Cu$

$=0.80-0.34=0.46 V \text { (Feasible) }$

3. $\mathbf{\mathrm{Fe}^{3+}{(a q)}+\mathrm{Br}_{(a q)}^{-} \rightarrow \mathrm{Fe}^{2+}{ }_{(a q)}+\frac{1}{2} \mathrm{Br}_{2(\mathrm{~g})}}$

Ans: $\mathrm{Fe}^{3+}{(a q)}+\mathrm{Br}_{(a q)}^{-} \rightarrow \mathrm{Fe}^{2+}{ }_{(a q)}+\frac{1}{2} \mathrm{Br}_{2(\mathrm{~g})}$

$E_{c e l l}^{o}=0.77-1.09=-0.32 v(\text { Not feasible })$

4. $A g_{(s)}+F e^{3+}_{(a q)} \rightarrow A g^{+}_{(a q)}+F e^{2+}(a q)$

Ans: $A g_{(s)}+F e^{3+}_{(a q)} \rightarrow A g^{+}_{(a q)}+F e^{2+}(a q)$

$E_{c e l l}^{o}=0.77-0.80=-0.03 v(\text { not feasible })$

5. $\frac{1}{2} B r_{2(g)}+F e^{2+}(a q) \rightarrow B r_{(a q)}^{-} F e^{3+}(a q)$

Ans: $\frac{1}{2} B r_{2(g)}+F e^{2+}(a q) \rightarrow B r_{(a q)}^{-} F e^{3+}(a q)$

$E_{c e l l}^{o}=1.09-0.77=0.32 V(\text { Feasible })$

18. Predict the products of electrolysis of the following:

1. An aqueous solution of \[{\text{AgN}}{{\text{O}}_{\text{3}}}\] with silver electrodes.

Ans. ${\text{AgN}}{{\text{O}}_{\text{3}}}{\text{(s) }}\xrightarrow{{}}{\text{ A}}{{\text{g}}^{\text{ + }}}{\text{(aq)  +  N}}{{\text{O}}_{\text{3}}}^{\text{ - }}{\text{(aq)}}$

${{\text{H}}_{\text{2}}}{\text{O}}\overset {} \leftrightarrows {\text{ }}{{\text{H}}^{\text{ + }}}{\text{  +  O}}{{\text{H}}^{\text{ - }}}$

At cathode: The discharge potential of ${\text{A}}{{\text{g}}^ + }$ ions is lower than that of ${{\text{H}}^ + }$ions. As a result, Ag ions will be deposited as ${\text{Ag}}$rather than ${{\text{H}}^ + }$ ions.

At anode: When the ${\text{Ag}}$ anode is attacked by ${\text{N}}{{\text{O}}_{\text{3}}}^-$ ions, the ${\text{Ag}}$ dissolves and forms ions in the solution.

${\text{Ag(s)}}\xrightarrow{{}}{\text{A}}{{\text{g}}^{\text{ + }}}{\text{(aq)  +  }}{{\text{e}}^{\text{ - }}}$

2. An aqueous solution of \[{\text{AgN}}{{\text{O}}_{\text{3}}}\]  with platinum electrodes.

Ans. At cathode: The discharge potential of ${\text{A}}{{\text{g}}^ + }$ ions is lower than that of ${{\text{H}}^ + }$ions. As a result, Ag ions will be deposited as ${\text{Ag}}$rather than ${{\text{H}}^ + }$ ions.

At anode: Because the anode is not attackable, ${\text{OH}}$ions have a lower discharge potential than${\text{N}}{{\text{O}}_{\text{3}}}^ - $ions. As a result, ${\text{OH}}$ will be evacuated first, followed by ${\text{N}}{{\text{O}}_{\text{3}}}^ - $ions, which will disintegrate and release ${{\text{O}}_2}$.

${\text{OH}}_{}^ -  \to {\text{OH}} + {{\text{e}}^ - }$

$4{\text{OH}} \to 2{{\text{H}}_2}{{\text{O}}_{(1)}} + {{\text{O}}_{2(g)}}$

3.  A dilute solution of \[{{\text{H}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}}\] with platinum electrodes.

Ans. ${{\text{H}}_2}{\text{S}}{{\text{O}}_4} \to 2{{\text{H}}^{\text{ + }}} + {\text{S}}{{\text{O}}_4}^{2 - }$

${{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{H  +  O}}{{\text{H}}^ - }$

At cathode: ${{\text{H}}^ + } + {{\text{e}}^ - } \to {\text{H}}$

${\text{H}} + {\text{H}} \to {{\text{H}}_{2(\;{\text{g}})}}$

At anode: ${\text{O}}{{\text{H}}^ - } \to {\text{OH}} + {{\text{e}}^ - }$

$4{\text{OH}} \to 2{{\text{H}}_2}{\text{O}} + {{\text{O}}_{2(g)}}$

Therefore, Hydrogen gas is released at the cathode and ${{\text{O}}_2}$ gas at the anode.

4. An aqueous solution of \[{\text{CuC}}{{\text{l}}_{\text{2}}}\] with platinum electrodes.

Ans. ${\text{CuC}}{{\text{l}}_{\text{2}}} \to {\text{C}}{{\text{u}}^{2 + }} + 2{\text{Cl}}_{}^ - $

${{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{H  +  O}}{{\text{H}}^ - }$

At cathode:${\text{C}}{{\text{u}}^{2 + }}$ ions will be reduced more than ${{\text{H}}^ + }$ ions, resulting in copper deposition at the cathode. 

${\text{C}}{{\text{u}}^{2 + }} + 2{{\text{e}}^ - } \to {\text{Cu}}$

At anode: \[{\text{C}}{{\text{l}}^{\text{ - }}}\]ions will be released first, followed by ${\text{O}}{{\text{H}}^{\text{ - }}}$ ions that will stay in solution. ${\text{C}}{{\text{l}}^{\text{ - }}} \to {\text{Cl}} + {{\text{e}}^ - }$

${\text{Cl}} + {\text{Cl}} \to {\text{C}}{{\text{l}}_{2(\;{\text{g}})}}$

Hence, copper will get set down on the cathode and ${\text{C}}{{\text{l}}_2}$ gas will be liberated at the anode.

Quick Overview of Topics: Class 12 Chemistry Chapter 2 - Electrochemistry 

Class 12 Chemistry Chapter 2 NCERT Solutions -Quick Overview of Detailed Structure of Topics and Subtopics Covered.

Class 12 NCERT Solutions Chapter 2 Important Formulas and Concepts 

Class 12 NCERT solutions help the students to go through the formulas easily. Here,   find the Important formulas of Chapter 2- Electrochemistry to crack your exams.

1. Nernst Equation: This equation relates the equilibrium potential of an electrochemical cell to the concentrations of the reactants and products involved. It's given as:

\[ E = E^\circ - \frac{0.0592}{nlog Q}\]

2. Gibbs Free Energy Change (ΔG): In electrochemistry, this concept is crucial as it determines whether a reaction is spontaneous or not. The relationship between Gibbs free energy change, cell potential, and temperature is given by:\[ \Delta G = -nFE \]

Benefits of Referring to Vedantu’s NCERT Solutions for Class 12 Chemistry Chapter 2

The Vedantu’s Class 12 NCERT Solutions of Chemistry provided here in PDFs offer various benefits, including:

1. Comprehensive Coverage: Detailed explanations and step-by-step solutions for all topics.

2. Expert Guidance: Curated by experienced educators, ensuring accurate and insightful answers.

3. Clarity and Precision: Clear, concise, and easy-to-understand explanations using precise scientific terminology.

4. Exam Preparation: Aligned with the latest CBSE syllabus, with practice questions and sample papers.

5. Conceptual Understanding: In-depth analysis of key electrochemical concepts and real-life applications.

6. Accessibility: Free PDF download for offline access and easy topic navigation.

7. Enhanced Problem-Solving Skills: Solutions to a variety of problems to strengthen analytical skills.

8. Interactive Learning: Supplementary video lessons and interactive sessions available on Vedantu’s platform.

Study Material Links for Class 12 Chemistry Chapter 2 Electrochemistry  

Students can access extra study materials on electrochemistry. These resources are available for download and offer additional support for your studies.

Conclusion

Vedantu's Electrochemistry Class 12 NCERT solutions for CBSE Chemistry Chapter 2 provide a comprehensive and effective resource for students studying this topic. The solutions cover all the important concepts and exercises outlined in the NCERT textbook, ensuring that students have a clear understanding of electrochemistry. Vedantu's solutions are well-structured and easy to follow, making it easier for students to grasp complex concepts and solve problems. The explanations are detailed and thorough, addressing common difficulties and providing step-by-step solutions. With Vedantu's Electrochemistry Class 12 NCERT solutions, students can enhance their understanding of electrochemistry and improve their performance in examinations. Overall, Vedantu's solutions are a valuable tool for Class 12 Chemistry students.

NCERT Solutions Class 12 Chemistry | Chapter-wise Links

Access Vedantu’s chapter-wise NCERT Chemistry Class 12 Solutions PDFs below for all other chapters.

NCERT Solutions Class 12 Chemistry - Related Links