
A ball connected with string is released at an angle $45^{\circ}$ with the vertical as shown in the figure. Then the acceleration of the box at this instant will be [Mass of the box is equal to the mass of the ball].
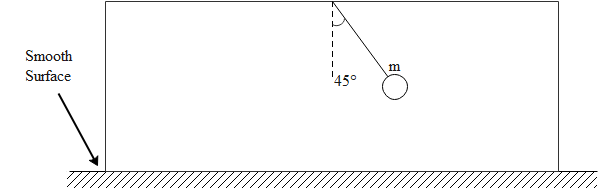
(A) g/4
(B) g/3
(C) g/2
(D) None of these
Answer
125.1k+ views
Hint: We know that tension is nothing but the drawing force acting on the body when it is hung from objects like chain, cable, string etc. It is represented by T. The direction of tension is the pull which is given the name tension. Thus, the tension will point away from the mass in the direction of the string or rope. In case of the hanging mass, the string pulls it upwards, so the string or rope exerts an upper force on the mass and the tension will be on the upper side. The tension force is the force that is transmitted through a string, rope, cable or wire when it is pulled tight by forces acting from opposite ends. The tension force is directed along the length of the wire and pulls equally on the objects on the opposite ends of the wire. Based on this concept we have to solve this question.
Complete step by step answer
We know that:
$T\cos \theta =mg$
Here T signifies the tension that is present in the string.
$T=\dfrac{mg}{\cos \theta }$
$T\sin \theta =ma$$T\sin \theta =ma$
Now we have to find the value of a.
So, we can say that:
$a=\dfrac{T\sin \theta }{m}=g\tan \theta$, here the value of $\theta ={{45}^{{}^\circ }}$.
Therefore, we can say that $a=g$.
So now the acceleration of the centre of mass is all zero. So, we can say that:
$\dfrac{ma-(m+m){{a}_{1}}}{m+(m+m)}=0$
So, the value of ${{a}_{1}}=\dfrac{g}{2}$
Hence the correct answer is option C.
Note: We should know that the weight of an object may be thought of as acting at a single point called its centre of mass. Depending on the object's shape, its centre of mass can be inside or outside it. The weight of an object and its mass are directly proportional. The centre of mass of an object is the point at which the object can be balanced. The centre of mass is useful because problems can often be simplified by treating a collection of masses as one mass at their common centre of mass. The weight of the object then acts through this point. In the human form the centre of mass has no fixed point but is dependent on the position of the performer at any given time. Due to the body composition the centre of mass of all athletes varies, as bone, fat, tissue and muscle all contribute to total mass and are in different proportions in each performer.
Complete step by step answer
We know that:
$T\cos \theta =mg$
Here T signifies the tension that is present in the string.
$T=\dfrac{mg}{\cos \theta }$
$T\sin \theta =ma$$T\sin \theta =ma$
Now we have to find the value of a.
So, we can say that:
$a=\dfrac{T\sin \theta }{m}=g\tan \theta$, here the value of $\theta ={{45}^{{}^\circ }}$.
Therefore, we can say that $a=g$.
So now the acceleration of the centre of mass is all zero. So, we can say that:
$\dfrac{ma-(m+m){{a}_{1}}}{m+(m+m)}=0$
So, the value of ${{a}_{1}}=\dfrac{g}{2}$
Hence the correct answer is option C.
Note: We should know that the weight of an object may be thought of as acting at a single point called its centre of mass. Depending on the object's shape, its centre of mass can be inside or outside it. The weight of an object and its mass are directly proportional. The centre of mass of an object is the point at which the object can be balanced. The centre of mass is useful because problems can often be simplified by treating a collection of masses as one mass at their common centre of mass. The weight of the object then acts through this point. In the human form the centre of mass has no fixed point but is dependent on the position of the performer at any given time. Due to the body composition the centre of mass of all athletes varies, as bone, fat, tissue and muscle all contribute to total mass and are in different proportions in each performer.
Recently Updated Pages
JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

JEE Main Login 2045: Step-by-Step Instructions and Details

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Fluids

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement




