Units and Measurements Class 11 Notes - CBSE Physics Chapter 1

Section–A (1 Mark Questions)

1. What is an error? 

Ans. An error is a mistake of some kind causing an error in your results, so the result is not accurate.

2. Find the number of the significant figures in $11\cdot 118\times 10^{-6}V$ .

Ans. The number of significant figures is 5 as 10−6 does not affect this number.

3. A physical quantity P is given by $P=\dfrac{A^{5}B^{\dfrac{1}{2}}}{C^{-4}D^{\dfrac{3}{2}}}$ . Find the quantity which brings in the maximum percentage error in P.

Ans. Quantity C has maximum power. So it brings maximum error in P.

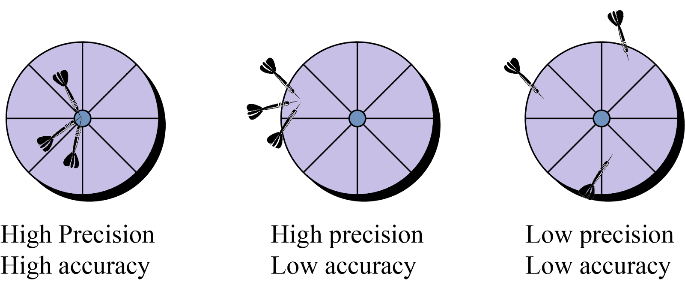
4. What is the difference between accuracy and precision?

Ans. Accuracy is an indication of how close a measurement is to the accepted value.

• An accurate experiment has a low systematic error.

Precision is an indication of the agreement among a number of measurements.  

• A precise experiment has a low random error.

5. Find the value of a for which $m=\dfrac{1}{\sqrt{3}}$ is a root of the equation $am^{2}+(\sqrt{3}-\sqrt{2})m-1=0$ .

Ans. Put $m=\dfrac{1}{\sqrt{3}}\Rightarrow \dfrac{a}{3}+(\sqrt{3}-\sqrt{2})\dfrac{1}{\sqrt{3}}-1=0$

$\Rightarrow a_+(3-\sqrt{6})-3=0$

So, a = $\sqrt{6}$

Section – B (2 Marks Questions)

6. A force F is given by $F=at+bt^{2}$ , where t is time. What are the dimensions of a and b?

Ans. From the principle of dimensional homogeneity $\left [ F \right ]=\left [ at \right ]\therefore \left [ a \right ]=\left [ \dfrac{F}{t} \right ]=\left [ \dfrac{MLT^{-2}}{T} \right ]=\left [ MLT^{-3} \right ]$

Similarly, $\left [ F \right ]=\left [ bt^{2} \right ]\therefore \left [ b \right ]=\left [ \dfrac{F}{t^{2}} \right ]=\left [ \dfrac{MLT^{-2}}{T^{2}} \right ]=\left [ MLT^{-4} \right ]$ .

7. Let l, r, c and v represent inductance, resistance, capacitance and voltage, respectively. Find the dimension of 1/rcv in SI units.  

Ans. Dimension of inductance = [M1L2T−2A−2] = [l]

Dimension of capacitance = [M−1L−2T4A2] = [c]

Dimension of resistance = [M1L2T−3A−2] = [r]

Dimension of voltage = [M1L2T−3A−1] = [v]

Dimension of l/rcv = 

M1L2T−2A−2] / [M−1L2T4A2][M1L2T−3A−2]

[M1L2T−3A−1]
= [ML2T−2A−2]/[ML2T−2A−1]

= [A−1]

8. P represents radiation pressure, c represents speed of light and S represents radiation energy striking unit area per sec. Find the non zero integers x, y, z such that $P^{x}S^{y}c^{z}$ is dimensionless.

Ans. Try out the given alternatives.

When x = 1, y = −1, z = 1

$P^{x}S^{y}c^{z}=P^{-1}S^{-1}c^{1}=\dfrac{Pc}{S}$

$=\dfrac{\left [ ML^{-1}T^{-2} \right ]\left [ LT^{-1} \right ]}{\left [ \dfrac{ML^{2}T^{-2}}{L^{2}T} \right ]}=\left [ M^{0}L^{0}T^{0} \right ]$

9. The length and breadth of a metal sheet are 3.124 m and 3.002 m respectively. Find the area of this sheet upto correct significant figure is

Ans. $A=3\cdot 124m\times 3\cdot 002m$

$A=\dfrac{9\cdot 738248}{248m^{2}}$

$=9\cdot 378m^{2}$

10. A certain body weighs 22.42 gm and has a measured volume of 4.7 cc. The possible errors in the measurement of mass and volume are 0.01 gm and 0.1 cc. Then find the maximum error in the density.

Ans. $D=\dfrac{M}{V}\therefore %\dfrac{\Delta D}{D}=%\dfrac{\Delta M}{M}+%\dfrac{\Delta V}{V}=\left ( \dfrac{0\cdot 01}{22\cdot 42}-\dfrac{0\cdot 1}{4\cdot 7} \right )\times 100=2%$

PDF Summary - Class 11 Physics Units and Measurements & Basic Mathematics Notes (Chapter 1)

Units:

A unit can be defined as an internationally accepted standard for measuring quantities.

• Measurement has been included of a numeric quantity along with a specific unit.

• The units in the case of base quantities (such as length, mass etc.) are defined as Fundamental unitfs.

• Derived units are the units that are the combination of fundamental units. 

• Fundamental and Derived units constitute together as a System of Units.

• An internationally accepted system of units can be defined as Système Internationale d’ Unites (This is how the International System of Units is represented in French) or SI. In 1971, it was produced and recommended by General Conference on Weights and Measures.

• The table shown below is the list of 7 base units mentioned by SI.

There are two units along with it. They are, radian or rad (unit for plane angle) and steradian or sr (unit for solid angle). Both of these are dimensionless.

2.3.1. Parallax Method-Measurement of large distances:

• Parallax can be defined as a displacement or difference in the apparent position of a body viewed along two various lines of sight and is calculated by the angle or semi-angle of inclination between those two lines. The basis is called the distance between the two viewpoints.

Calculating the distance of a planet using parallax method:

In the similar way,

$\text{ }\!\!\alpha\!\!\text{ =}\frac{\text{d}}{\text{D}}$

Where $\text{ }\!\!\alpha\!\!\text{ }$ be the planet’s angular size (angle subtended by d at earth) and d will be the diameter of the planet. If two diametrically opposite points of the planet are viewed, then $\text{ }\!\!\alpha\!\!\text{ }$ be the angle between the direction of the telescope.

2.3.2. Measuring very small distances:

For measuring the distances as low as size of a molecule, electron microscopes will be used. These will include electrons beams controlled by electric and magnetic fields.

• Electron microscopes will be having a resolution of 0.6 Å or Angstroms.

• Electron microscopes are used for resolving atoms and molecules when we use a tunnelling microscopy, it will be possible for estimating size of molecule. Calculating size of molecule of Oleic acid. Oleic acid will be a soapy liquid with large molecular size of the order of ${{10}^{-9}}\text{ m}$. The following steps are used in determining the size of molecule:

• Dissolving $\text{1 c}{{\text{m}}^{\text{3}}}$ of oleic acid in alcohol for producing a solution of $\text{20 c}{{\text{m}}^{\text{3}}}$.Consider $\text{1 c}{{\text{m}}^{\text{3}}}$ of above solution and using alcohol dilute it to a concentration of $\text{20 c}{{\text{m}}^{\text{3}}}$. So, the concentration of oleic acid in the solution will become $\left( \frac{1}{20\times 20} \right)\text{ c}{{\text{m}}^{\text{3}}}$ of oleic acid/$\text{c}{{\text{m}}^{\text{3}}}$ of solution.

• Then add lycopodium powder on the surface of water in a trough and keep one drop of above solution. In a circular molecular thick film, the oleic acid in the solution will spread over water.

• Calculate the diameter of the above circular film by the use of below calculations.

• When n –Number of drops of solution in water, t – Thickness of the film, V –Volume of each drop, A – Area of the film.

• Total volume of n drops of solution $\text{=nVc}{{\text{m}}^{\text{3}}}$ 

• The amount of Oleic acid in this solution$\text{=nV}\left( 120\times 20 \right)\text{c}{{\text{m}}^{\text{3}}}$

• Thickness of the film =$\text{t=}\frac{\text{Volume of the film}}{\text{Area of the film}}$

• $\text{t=}\frac{\text{nV}}{\text{20 }\!\!\times\!\!\text{ 20A}}\text{cm}$

Special Length units:

Measurement of Mass:

Mass can be defined usually in terms of kg but a unified atomic mass unit (u) will be used for atoms and molecules.

\[\text{1 u=}\frac{\text{1}}{\text{12}}\]of the mass of an atom of isotope of carbon 12 which will be included of the mass of electrons (\[\text{1}\text{.66 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-27}}}\text{ kg}\]).

Mass of planets is measured by the use of gravitational methods and mass of atomic particles are measured by the usage of the mass spectrograph (radius of trajectory will be proportional to the mass of charged particle which is in motion in uniform electric and magnetic field), apart from using balances for normal weights.

Range of Mass:

Measurement of Time:

Time has been calculated by the use of a clock. Atomic standard of time being now used, measured by the Cesium or Atomic clock, as a standard.

• A second will be equivalent to 9,192,631,770 vibrations of radiation from the transition between two hyperfine levels of an atom of cesium-133 in a Cesium clock.

• The caesium clock will be working on the vibration of the Cesium atom which is identical to vibrations of quartz crystal in a quartz wristwatch and balance wheel in a normal wristwatch.

• National standard time and frequency will be maintained by 4 atomic clocks. Indian standard time will be maintained by a Cesium clock at National Physical Laboratory (NPL), New Delhi.

• Caesium clocks will be perfectly accurate and the uncertainty will be very low 1 part in 1013 which means no more than \[\text{3  }\!\!\mu\!\!\text{ s}\] will be lost or gained in a year.

Range of Time:

Accuracy and Precision of Instruments:

• Any uncertainty which is formed from the calculation by a measuring instrument can be defined as an error. This can be categorised as systematic or random.

• The resolution of the measured value to the true value can be defined as the accuracy of a measurement.

• The resolution of numerous of measurements of an identical quantity under the same conditions can be called precision.

• Till 1 (less precise) and 2 (more precise) decimal places in the same order, has been used when the true value of a specific length is 3.678 cm and two instruments with various resolutions. When first measures the length as 3.5 and the second as 3.38 then the first will be having more accuracy but precision will be less while the second will be having less accuracy and more precision.

Types of Errors- Systematic Errors:

Systematic errors are errors that can either be positive or negative. The following types are:

1. Instrumental errors: which arouse from calibration error or imperfect design in the instrument. Zero error in a weighing scale, Worn off-scale are a few examples of instrument errors.

2. Imperfections in experimental techniques when the technique is not correct (measurement of the temperature of the human body by keeping thermometer under armpit resulting in lower temperature than actual can be considered as an example) and because of the external conditions such as temperature, wind, humidity, and these kinds of errors happen.

3. Personal errors: Errors happening because of human carelessness, lack of proper setting, taking down incorrect reading are defined as personal errors.

The removal of these errors will be:

• By taking the proper instrument and properly calibrating it.

• By experimenting under correct atmospheric conditions and techniques.

• Avoiding human bias as far as possible.

Random Errors:

Errors which is happening at random with respect to sign and size are defined as Random errors.

• These kind of errors happens because of the unpredictable fluctuations in experimental conditions such as temperature, voltage supply, mechanical vibrations, personal errors etc.

Least Count Error:

The smallest value which is measurable by the use of a measuring instrument is called its least count. The least count error is the error related to the least count of the instrument.

• Least count errors is minimizable by the usage of equipments of higher precision/resolution and improving experimental techniques (take several readings of a measurement and then calculate a mean).

Errors in a series of Measurements. 

Assume that the values got in several measurement are \[{{\text{a}}_{\text{1}}},{{\text{a}}_{2}},{{\text{a}}_{3}}....{{\text{a}}_{\text{n}}}\].

Arithmetic mean,

\[{{\text{a}}_{\text{mean}}}\text{=}\frac{\left( {{\text{a}}_{\text{1}}}\text{+}{{\text{a}}_{\text{2}}}\text{+}{{\text{a}}_{\text{3}}}\text{+}...\text{+}{{\text{a}}_{\text{n}}} \right)}{\text{n}}\]

\[{{\text{a}}_{\text{mean}}}\text{=}\sum\limits_{\text{i=1}}^{\text{n}}{\frac{{{\text{a}}_{\text{i}}}}{\text{n}}}\]

• Absolute Error can be defined as the magnitude of the difference between the true value of the quantity and absolute error of the measurement can be defined as the individual measurement value. It is represented as \[\left| \text{ }\!\!\Delta\!\!\text{ a} \right|\] (or Mod of Delta a). The mod value will be positive always even if \[\text{ }\!\!\Delta\!\!\text{ a}\] is negative. The individual errors will be:

$\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{1}}}\text{=}{{\text{a}}_{\text{mean}}}\text{-}{{\text{a}}_{\text{1}}}$ 

$\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{2}}\text{=}{{\text{a}}_{\text{mean}}}\text{-}{{\text{a}}_{2}}$$....................$

$ .....................$ 

$\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{n}}}\text{=}{{\text{a}}_{\text{mean}}}\text{-}{{\text{a}}_{\text{n}}}$ 

• Mean absolute error can be explained as the arithmetic mean of all absolute errors. It has been represented as \[\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}\].

\[\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}=\left| \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{1}} \right|+\left| \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{2}} \right|+\left| \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{3}} \right|+....+\left| \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{n}}} \right|\]

\[\text{ }\!\!\Delta\!\!\text{

}{{\text{a}}_{\text{mean}}}\text{=}\sum\limits_{\text{i=1}}^{\text{n}}{\frac{\left| \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{i}}} \right|}{\text{n}}}\]

In the case of every single measurement, the value of ‘a’ is always in the range \[{{\text{a}}_{\text{mean}}}\pm \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}\]

So, \[\text{a=}{{\text{a}}_{\text{mean}}}\pm \text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}\]

Or, \[{{\text{a}}_{\text{mean}}}-\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}\le \text{a}\le {{\text{a}}_{\text{mean}}}+\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}\]

• Relative Error can be defined as the mean absolute error divided by the mean value of the quantity measured.

Relative Error \[=\frac{\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}}{{{\text{a}}_{\text{mean}}}}\]

• Percentage Error can be defined as the relative error expressed in percentage. It is denoted by \[\text{ }\!\!\delta\!\!\text{ a}\].

\[\text{ }\!\!\delta\!\!\text{ a=}\frac{\text{ }\!\!\Delta\!\!\text{ }{{\text{a}}_{\text{mean}}}}{{{\text{a}}_{\text{mean}}}}\text{ }\!\!\times\!\!\text{ 100}\] (Not in the updated syllabus)

Combinations of Errors

When a quantity is dependent on two or more other quantities, the combination of errors in the two quantities will be helping for determining and predicting the errors in the resultant quantity. There are various procedures for this.

Consider two quantities A and B have values as A ±ΔA and B ± ΔB. Let Z be the result and ΔZ is the error because of the combination of A and B.

Significant Figures

Every measurement gives us an output in a number that is included of reliable digits and uncertain digits.

Reliable digits added with the first uncertain digit can be defined as significant digits or significant figures. This is representing the precision of measurement which is dependent on least count of instrument used for measurement.

The period of oscillation of a pendulum is 1.62 s can be taken as an example. Here 1 and 6 will be the reliable and 2 is uncertain. Hence, the measured value will be having three significant figures.

Rules for the determination of number of significant figures

• All non-zero digits will be significant.

• Irrespective of decimal place, all zeros between two non-zero digits will be significant irrespective of decimal place.

• Zeroes before non-zero digits and after decimal are not considered as significant, for a value less than 1. Zero present before decimal place in case of these number will be insignificant always.

• Trailing zeroes in case of a number without any decimal place will be insignificant.

• Trailing zeroes in case of a number with decimal place will be significant.

Cautions for removing ambiguities in calculating number of significant figures

• Variation of units will not change number of significant digits. As an example, 

$\text{4}\text{.700 m=470}\text{.0 cm}$ 

$\text{              =4700 mm}$ 

Here, first two quantities are having 4 but third quantity is having 2 significant figures.

• Make use of scientific notation for reporting measurements. Numbers must be shown in powers of 10 such as \[\text{a }\!\!\times\!\!\text{ 10b}\]where b is defined as order of magnitude. Example,

$\text{4}\text{.700 m = 4}\text{.700  }\!\!\times\!\!\text{  1}{{\text{0}}^{\text{2}}}\text{ cm }$

$\text{               = 4}\text{.700  }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{3}}}\text{ mm }$

$\text{               = 4}\text{.700  }\!\!\times\!\!\text{  1}{{\text{0}}^{\text{-3}}}\text{ km}$

Here, as the power of 10 is being irrelevant, number of significant figures will be 4.

• Multiplying or dividing exact numbers will be giving infinite number of significant digits. Example,\[\text{radius=}\frac{\text{diameter}}{\text{2}}\]. In this case, 2 can be represented as 2, 2.0, 2.00, 2.000 and so on.

Rules for Arithmetic operation with Significant Figures

Rules for Rounding off the uncertain digits

Rounding off will be essential for reducing the number of insignificant figures to hold to the rules of arithmetic operation with significant figures.

Rules for the determination of uncertainty in the results of arithmetic calculations

For calculating the uncertainty, below process must be used.

• Do summation of a lowest amount of uncertainty in the original numbers. Example uncertainty for 3.2 will be \[\pm 0.1\] and for 3.22 will be \[\pm 0.01\].

• Find out these in percentage also.

• The uncertainties get multiplied/divided/added/subtracted after the calculations.

• In the uncertainty, round off the decimal place for obtaining the end uncertainty result.

For example, for a rectangle, 

Suppose length,  \[\text{l=16}\text{.2 cm}\] and breadth, \[\text{b=10}\text{.1 cm}\]

After that, take \[\text{l=16}\text{.2}\pm \text{0}\text{.1 cm}\]or \[\text{l=16}\text{.2 cm}\pm \text{0}\text{.6  }\!\!%\!\!\text{ }\] and

breadth \[\text{=10}\text{.1 }\!\!\pm\!\!\text{ 0}\text{.1 cm}\]or \[\text{10}\text{.1 cm }\!\!\pm\!\!\text{ 1  }\!\!%\!\!\text{ }\]

When we multiply,

\[\text{area=length }\!\!\times\!\!\text{ breadth=163}\text{.62 c}{{\text{m}}^{\text{2}}}\text{ }\!\!\pm\!\!\text{ 1}\text{.6  }\!\!%\!\!\text{ }\]

Or \[\text{163}\text{.62}\pm \text{2}\text{.6 c}{{\text{m}}^{\text{2}}}\]

Hence after rounding off, area\[\text{=164}\pm \text{3 c}{{\text{m}}^{\text{2}}}\].

Therefore \[\text{3 c}{{\text{m}}^{\text{2}}}\]will be the uncertainty or the error in estimation.

Rules

1. In the case of a set experimental data of ‘n’ significant figures, the result must be accurate to ‘n’ significant figures or less (only in case of subtraction).

For example \[\text{12}\text{.9-7}\text{.06=5}\text{.84 or 5}\text{.8}\](when we round off to least number of decimal places of original number).

2. The relative error of a value of number mentioned to significant figures will be dependent on n and on the number itself.

As an example, say accuracy for two numbers 1.02 and 9.89 be \[\pm \text{0}\text{.01}\]. But relative errors are:

For \[\text{1}\text{.02,}\left( \frac{\text{ }\!\!\pm\!\!\text{ 0}\text{.01}}{\text{1}\text{.02}} \right)\text{ }\!\!\times\!\!\text{ 100  }\!\!%\!\!\text{ =}\pm \text{1  }\!\!%\!\!\text{ }\]

For\[\text{9}\text{.89,}\left( \frac{\text{ }\!\!\pm\!\!\text{ 0}\text{.01}}{\text{9}\text{.89}} \right)\text{ }\!\!\times\!\!\text{ 100  }\!\!%\!\!\text{ =}\pm 0.\text{1  }\!\!%\!\!\text{ }\]

Therefore, the relative error will be dependent upon number itself.

3. The results in the intermediate step of a multi-step computation should be found to have one significant figure more in all the measurement than the number of digits in the least precise measurement.

For example:\[\frac{1}{9.58}=0.1044\]

Now, \[\frac{1}{0.104}=9.56\] and \[\frac{1}{0.1044}=9.58\]

Therefore, taking one extra digit will be providing more precise outputs and reduces rounding off errors.

Dimensions of a Physical Quantity

The powers (exponents) to which base quantities are raised to represent that quantity can be defined as dimensions of a physical quantity. They are figured as the square brackets around the quantity.

• Dimensions of the 7 base quantities has been considered as – Length [L], time [T], Mass [M], thermodynamic temperature [K], luminous intensity [cd], electric current [A] and amount of substance [mol].

For example,

$\text{Volume=Length }\!\!\times\!\!\text{ Breadth }\!\!\times\!\!\text{ Height}$

$text{=}\left[ \text{L} \right]\text{ }\!\!\times\!\!\text{ }\left[ \text{L} \right]\text{ }\!\!\times\!\!\text{ }\left[ \text{L} \right]\text{=}{{\left[ \text{L} \right]}^{\text{3}}}$ 

$\text{Force=Mass }\!\!\times\!\!\text{ Acceleration}$

$\text{=}\frac{\left[ \text{M} \right]\left[ \text{L} \right]}{{{\left[ \text{T} \right]}^{\text{2}}}}\text{=}\left[ \text{M} \right]\left[ \text{L} \right]{{\left[ \text{T} \right]}^{\text{-2}}}$

• The other dimensions for a quantity will be always 0. As an example, in the case of volume only length has 3 dimensions but the mass, time

etc will be having 0 dimensions. Zero dimension is shown by superscript 0 like \[\left[ {{\text{M}}^{0}} \right]\].

Dimensions will not affect the magnitude of a quantity Dimensional formula and Dimensional Equation

The expression which is representing how and which of the base quantities represent the dimensions of a physical quantity is defined as Dimensional Formula.

An equation we got after equating a physical quantity with its dimensional formula is a Dimensional Equation.

Dimensional Analysis

• The physical quantities which is having similar dimensions only can be added and subtracted. This can be named as the principle of homogeneity of dimensions.

• Dimensions are multipliable and can be cancelled as normal algebraic methods.

• Quantities on both sides should always have identical dimensions, in mathematical equations.

• Arguments of special functions such as trigonometric, logarithmic and ratio of similar physical quantities will be dimensionless.

• Equations will be uncertain to the extent of dimensionless quantities.

As an example, say Distance = Speed x Time. In Dimension terms, 

\[\left[ \text{L} \right]\text{=}\left[ \text{L}{{\text{T}}^{\text{-1}}} \right]\text{ }\!\!\times\!\!\text{ }\left[ \text{T} \right]\]

As the dimensions can be cancelled like we do in algebra, dimension \[\left[ \text{T} \right]\] will get cancelled and the equation will be \[\left[ \text{L} \right]\text{=}\left[ \text{L} \right]\].

Applications of Dimensional Analysis

When we check the Dimensional Consistency of equations

• A dimensionally correct equation should be having identical dimensions on both sides of the equation.

• There is no need for a dimensionally correct equation to be a correct equation but a dimensionally incorrect equation will be always incorrect. Dimensional validity can be tested but not calculate the correct relationship between the physical quantities.

Example, \[\text{x=}{{\text{x}}_{\text{0}}}\text{+}{{\text{ }\!\!\nu\!\!\text{ }}_{\text{0}}}\text{t+}\left( \frac{\text{1}}{\text{2}} \right)\text{a}{{\text{t}}^{\text{2}}}\]

Or, Dimensionally, \[\left[ \text{L} \right]\text{=}\left[ \text{L} \right]\text{+}\left[ \text{L}{{\text{T}}^{\text{-1}}} \right]\left[ \text{T} \right]\text{+}\left[ \text{L}{{\text{T}}^{\text{-2}}} \right]\left[ {{\text{T}}^{\text{2}}} \right]\]

Where, \[\text{x}\] be the distance travelled in time t,

\[{{\text{x}}_{0}}\]– starting position,

\[{{\nu }_{0}}\]- initial velocity,

\[\text{a}\]– uniform acceleration.

Dimensions on both sides will be [L] because [T] get cancelled out. Therefore this will be dimensionally correct equation.

Deducing relation among physical quantities

• For deducing a relation among physical quantities, we must know the dependence of one quantity over others (or independent variables) and assume it as a product type of dependence.

• Dimensionless constants will not be obtainable by the use of this method.

We can take an example, 

\[\text{T=k}{{\text{l}}^{\text{x}}}{{\text{g}}^{\text{y}}}{{\text{m}}^{\text{z}}}\]

Or,

$\left[ {{\text{L}}^{\text{0}}}{{\text{M}}^{\text{0}}}{{\text{T}}^{\text{1}}} \right]\text{=}{{\left[ {{\text{L}}^{\text{1}}} \right]}^{\text{x}}}{{\left[ {{\text{L}}^{\text{1}}}{{\text{T}}^{\text{-2}}} \right]}^{\text{y}}}{{\left[ {{\text{M}}^{\text{1}}} \right]}^{\text{z}}}$ 

$\text{                =}\left[ {{\text{L}}^{\text{x+y}}}{{\text{T}}^{\text{-2y}}}{{\text{M}}^{\text{z}}} \right]$

This means that, \[\text{x+y=0,-2y=1 and z=0}\]. So \[\text{x=}\frac{1}{2}\text{,y=-}\frac{1}{2}\text{ and z=0}\].

Hence the original equation will be reduced to \[\text{T=k}\sqrt{\frac{\text{l}}{\text{g}}}\].

Units and Measurements Notes Physics Chapter 1 - Free PDF Download

Topics Covered under Physics Chapter 1 Class 11 Notes 

As mentioned in Vedantu’s Class 11 Physics Ch 1 Notes, an arbitrarily chosen and internationally accepted standard i.e. unit is used as a reference to express the measurement of a particular physical quantity.

Physical quantity = Numerical value x Unit. For example, Length of a ladder  = 5.5 m

Here 5.5 is a numerical value and m (metre) is the unit of length.

The units that can be expressed independently are called fundamental or base units. For example- mass is expressed in kilogram, length in metre, and time in second respectively are fundamental units.

The units for which a combination of the fundamental units is called derived units. Units of area and density which are m2, kg/m3 respectively are examples of derived units.

The International System of Units

The base units for length, mass and time in unit systems are: 

CGS System: centimetre, gram and second

FPS System: foot, pound and second

MKS System: metre, kilogram and second

SI System: This system is internationally accepted for measurement (Système Internationale d’ Unites). Length, mass, time, electric current, thermodynamic temperature, amount of substance and luminous intensity are expressed in metre(m), kilogram(kg), second(s), ampere(A), Kelvin(K), mole(mol) and candela(cd) respectively.

Apart from the above units, there are two supplementary base units:

(i) radian (rad) for angle

(Image to be added soon)

(ii) steradian (sr) for a solid angle.

(Image to be added soon)

Parallax Method of Measurement of Large Distances

This method is used to measure large distances like that of planets and stars from earth.

Some Units of Large Distance

1 light-year = 1 ly = 9.46 × 1015 m (the distance that light travels with a velocity of 3 × 108 m s–1 in 1 year) 

1 parsec = 3.08 × 1016 m (distance at which average radius of earth’s orbit subtends an angle of 1 arc second)

Estimation of Very Short Distances: The Size of a Molecule

In Chapter 1 Physics Class 11 Notes, one can learn how to measure the size of a molecule.

Some units of short length:

1 fermi = 1 f = 10–15 m 

1 angstrom = 1 Å = 10–10 m 

Errors In Measurement

The uncertainty while measuring a physical quantity is called an error.

(i) Systematic Errors:

• Instrumental errors

• A flaw in experimental technique or procedure

• Personal errors

(ii) Random Errors: Irregular errors due to unpredictable fluctuations in experimental conditions

• Least Count Error: associated with the resolution of the instrument.

• Absolute Error: amean = (a1 +a2 +a3 +...+an ) / n

∆a  = amean – measured value

• Mean Absolute Error: ∆amean = (|∆a1 |+|∆a2 |+|∆a3 |+...+ |∆an |)/n 

\[\sum_{i=1}^{n}\] |∆ai |/ni

• Relative Error :  ∆amean/ amean

• Percentage Error: δa = (∆amean/ amean) × 100 %

Combination of Errors

• An error of a sum or a difference

If Z=A+ B then  ∆Z =∆A + ∆B

if Z=A- B then ∆Z =∆A + ∆B

• An error of a product or a quotient
  If Z= A×B or Z=A/B 

error in ‘Z’ = ∆Z/Z= (∆A/A) + (∆B/B)

• Error in a quantity that has been raised to power:

If Z = Ak

then ∆Z/Z = K (∆A/A)

Significant Figures

Arithmetic Operations with Significant Figures

For addition, subtraction, multiplication and division the result has the same number of significant figures as that of the number with a minimum number of decimal places.

Rounding off the Uncertain Digits

If dropping digit < 5, then the previous digit is left unchanged. 

If dropping digit > 5, then the previous digit is raised by 1

If dropping digit = 5 followed by non-zero digits, then the previous digit is raised by 1

Dimensions of Physical Quantities

Dimension of :

Length=[L]

Mass=[M]

Time= [T]

Electric current=[A]

Temperature=[K]

Luminous intensity=[cd]

Amount of substance = [mol]. 

Dimensional equations represent physical entities in terms of their base quantities. 

For example, speed = (distance/time)

Dimensional equation of speed [v]= [M0 L T–1]

Importance of Vedantu’s Units and Measurements Class 11 Notes PDF Download

Vedantu's Units and Measurements Class 11 Notes offer students a valuable resource to grasp the fundamental concepts of physics. By using Vedantu's notes, students can enhance their problem-solving skills and develop a strong foundation in physics, empowering them to excel in their academic pursuits. Here are some points that explains the Importance of Units and Measurements Class 11 Notes PDF Download:

• Vedantu's Class 11 Physics Chapter 1 Notes provide a comprehensive understanding of fundamental concepts in physics.

• These notes cover topics such as SI units, dimensional analysis, and measurements with precision.

• They offer clear explanations and examples to aid in conceptual clarity and application of theories.

• Vedantu's notes facilitate effective revision and preparation for exams by condensing complex concepts into concise summaries.

• With Class 11 Units and Measurements Notes, students can enhance their problem-solving skills and achieve mastery in the subject, laying a strong foundation for future studies in physics.

What does Vedantu’s Free Study Material - Class 11 Units and Measurements Notes Provide?

• A hands-on experience in time management and paper pattern

• A vivid idea about the topic based marks weightage along with hierarchical study plan

• Explanatory videos and free mock test to enhance problem-solving skills

• Specially designed model papers and practice test by our eminent educators

Class 11 Units and Measurements Notes suffice for all the basic concepts and doubt clearance regarding measurements, units, dimensions and errors. The principles of physical quantities in Ch 1 Physics Class 11 Notes go a long way in building a strong foundation for the upcoming chapters.

Download CBSE Class 11 Physics Revision Notes 2024-25 PDF

Also, check CBSE Class 11 Physics revision notes for other chapters:

Units and Measurement & Basic Mathematics Chapter-Related Important Study Materials

It is a curated compilation of relevant online resources that complement and expand upon the content covered in a specific chapter. Explore these links to access additional readings, explanatory videos, practice exercises, and other valuable materials that enhance your understanding of the chapter's subject matter.

Conclusion

Class 11 Physics Chapter 1 Units and Measurements Notes offered by Vedantu is an excellent resource for students who want to excel in their physics studies. The Class 11 Units and Measurements Notes provide a comprehensive and detailed explanation of the concepts of units and measurement, including the SI units, dimensions, and errors, making it easier for students to understand and improve their physics skills. The notes also include practice exercises and questions that help students test their understanding of the chapter and prepare for their exams. Vedantu also provides interactive live classes and doubt-solving sessions to help students clarify their doubts and improve their understanding of the chapter. Overall, the Unit and Measurement Class 11 Notes PDF offered by Vedantu are an essential resource for students who want to improve their physics skills and score well in their exams.