Question

A ball is dropped from a height of $90m$ on a floor. At each collision with the floor, the ball loses one- tenth of its speed. Plot the speed- time graph of its motion between $t = 0$ to $12s$ .

Answer 1

Hint We need to find the time taken by the ball to reach the floor for the first collision. Thereby we shall decrease the velocity of the ball and then again compute the same. We will use the formula $v = u + at$ and $S = ut + \dfrac{1}{2}a{t^2}$, where $v$ is the final velocity, $u$ is the initial velocity, $t$ is time, $a$ is the acceleration, and $S$ is the displacement.

Complete Step by step solution The time for the first collision is the time taken by the ball to drop from $90m$.
We will find that using $S = ut + \dfrac{1}{2}a{t^2}$, where the initial velocity $u$ is $0$, the acceleration is equal to the acceleration due to gravity, and $S$ is given in the question to be $90m$ .
We substitute the above values in $S = ut + \dfrac{1}{2}a{t^2}$, to get
$ \Rightarrow - 90m = (0)t + \dfrac{1}{2}( - g){t^2}$
$ \Rightarrow - 180m = ( - g){t^2}$
The value of acceleration due to gravity is $g = 9.8m/{s^2}$.
$ \Rightarrow - 180m = ( - 9.8m/{s^2}){t^2}$
$ \Rightarrow {t^2} = \dfrac{{180m}}{{9.8m/{s^2}}}$, or $t = \sqrt {\dfrac{{180}}{{9.8}}} s = \dfrac{{30}}{7}s$.
At this time, the value of $v$ can be found using $v = u + at$, where $t = \dfrac{{30}}{7}s$, and $a = - 9.8m/{s^2}$.
$ \Rightarrow v = 0 + ( - 9.8)\dfrac{{30}}{7}$, as initial velocity is $0$,
$ \Rightarrow v = - 42m/s$.
It is given that the ball loses one- tenth of its speed. Thus the speed after the first collision is ${u_1} = \dfrac{9}{{10}}(42m/s) = 37.8m/s$
Now the next collision will happen when the ball has reached the maximum height and returned to the same speed but opposite sign, just before the second collision.
The time taken for the second collision is calculated using $v = u + at$, where we substitute value to get, $( - 37.8m/s) = (37.8m/s) + ( - 9.8m/{s^2}){t_1}$
$ \Rightarrow ( - 75.6m/s) = ( - 9.8m/{s^2}){t_1}$
On further simplifying the equation we get,
$ \Rightarrow {t_1} = \dfrac{{75.6}}{{9.8}}s$
$ \Rightarrow {t_1} = \dfrac{{54}}{7}s$.
This is the time between the first and the second collisions.
Thus the total time at which the second collision occurs is
 $t + {t_1} = \dfrac{{30}}{7} + \dfrac{{54}}{7} = \dfrac{{84}}{7} = 12s$
Therefore the second collision occurs at $12s$ after the ball is released from a height of $90m$.
Using these above information, we get the velocity-time graph as,


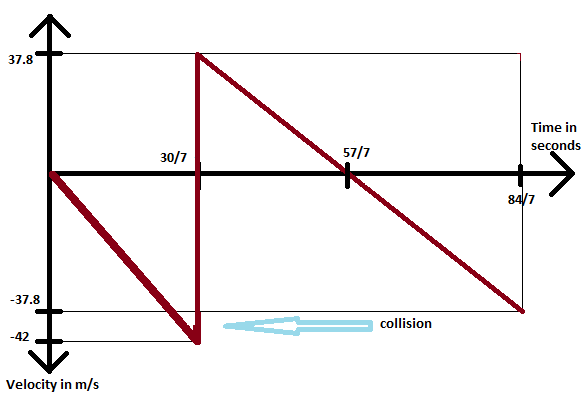
However, we require the speed- time graph and not the velocity- time graph.
Thus we will only take the absolute values of the velocities and use them for drawing the graph.

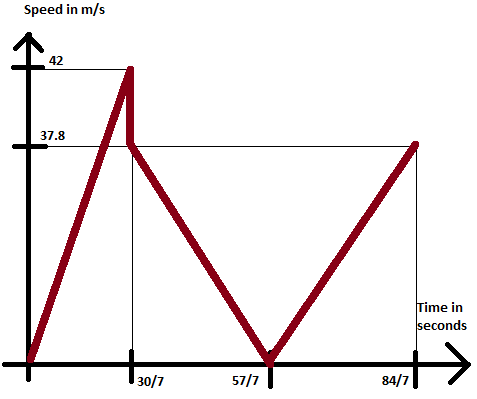
Here we have made the plot till before the second collision occurs.

Note Here we have assumed the sign convention as negative towards the earth and positive away from the acceleration due to gravity. Thus the signed value of acceleration due to gravity is $g = - 9.8m/{s^2}$ which is directed towards the earth.