
A ball rolls down an inclined plane and acquires a velocity
A.
B.
C.
D.
Answer
138.6k+ views
Hint: When a ball rolls down a rough plane in comparison to a smooth plane, there is an additional factor of friction acting against the downward acceleration of the rolling ball in case of a rough plane. So as a consequence the velocities will have a difference between them. Their exact relation can be concluded using Newtonian physics. And comparing it with the given options provides the right answer.
Formula Used:
Newton’s third law of motion:
Complete step by step answer:
When the ball moves down a rough plane, there are a total of four components of forces acting in it as shown in the figure below. The horizontal components cancel each other out as there is no horizontal displacement clearly. Similarly, for a ball rolling down a smooth plane there are three components of forces acting as shown below:
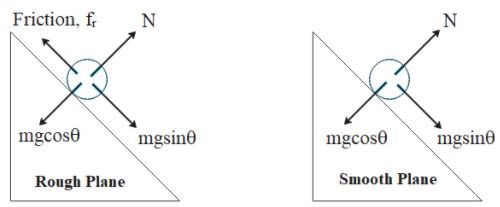
In case of the rough plane:
Let
So we have:
In case of the smooth plane:
Let
So we have:
From equation (1) and (2), it is clear that:
Using Newton’s third law of motion we have:
But we know that initially in both the cases the ball was at rest, so initial velocity is zero and at the endpoint the displacement is same so, we get:
So, it is true that
Clearly option C is incorrect and option B is incorrect.
The work done by the rolling ball will be zero as its instantaneous displacement is zero when it rolls down the rough plane. So option A is also incorrect.
When the ball rolls down a rough surface it acquires translational as well as rotational energy. Thus the kinetic energy of the ball rolling down will be greater than the kinetic energy of the other ball moving down on a smooth plane. Hence option D. is correct.
Therefore, the incorrect statements are A, B, and C.
Note: When a sphere or ball is rolled on a horizontal surface it slows down and eventually stops because the normal force does not pass through its center, rather it gets shifted towards the right. This in turn results in an anticlockwise torque, so the net torque causes an angular deceleration.
Formula Used:
Newton’s third law of motion:
Complete step by step answer:
When the ball moves down a rough plane, there are a total of four components of forces acting in it as shown in the figure below. The horizontal components cancel each other out as there is no horizontal displacement clearly. Similarly, for a ball rolling down a smooth plane there are three components of forces acting as shown below:

In case of the rough plane:
Let
So we have:
In case of the smooth plane:
Let
So we have:
From equation (1) and (2), it is clear that:
Using Newton’s third law of motion we have:
But we know that initially in both the cases the ball was at rest, so initial velocity is zero and at the endpoint the displacement is same so, we get:
So, it is true that
Clearly option C is incorrect and option B is incorrect.
The work done by the rolling ball will be zero as its instantaneous displacement is zero when it rolls down the rough plane. So option A is also incorrect.
When the ball rolls down a rough surface it acquires translational as well as rotational energy. Thus the kinetic energy of the ball rolling down will be greater than the kinetic energy of the other ball moving down on a smooth plane. Hence option D. is correct.
Therefore, the incorrect statements are A, B, and C.
Note: When a sphere or ball is rolled on a horizontal surface it slows down and eventually stops because the normal force does not pass through its center, rather it gets shifted towards the right. This in turn results in an anticlockwise torque, so the net torque causes an angular deceleration.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
EMI starts from ₹3,487.34 per month
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




