Question

A bi-convex lens formed with two thin Plano-convex lenses as shown in the figure. Refractive index of the first lens is $1.5$ and that of the second lens is $1.2$ both the curved surfaces are of the same radius of curvature $R = 14cm$. For this bi-convex lens, for an object distance of $40cm$, the image distance will be.

A) $ - 280.0cm$
B) $40.0cm$
C) $21.5cm$
D) $13.3cm$

Answer 1

Hint: We want to find the final position of image for that we must have the focal length of lens only then we can find the position of image. To find the focal length of a lens although we have two Plano-convex lenses, we have to find the focal length of a combination of these Lens. When we find combined focal length then simply we apply lens formula to find the distance of the image.

Complete step by step solution:
In the question the given data is
Radius of curvature of both lanes $14cm$ and refractive index of lens 1is ${n_1} = 1.5$ and lens 2 is ${n_2} = 1.2$

Step 1:We have to find the individual focal length of both lenses by using formula.
$\dfrac{1}{f} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ ....................... (1)
Where $n \Rightarrow $ refractive index of lens
And ${R_1} \Rightarrow $ radius of curvature of first surface of lens
${R_2} \Rightarrow $ Radius of curvature of second surface of lens
$f \Rightarrow $ Focal length of lens
So we apply this formula for the first lens. For first lens

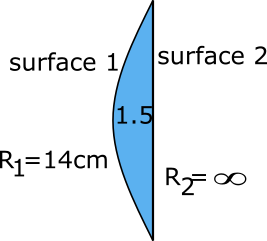
 Refractive index ${n_1} = 1.5$
${R_1} = 14cm$
${R_2} = \infty $ Because second surface is plane in first lens
Apply formula from eq (1)
$ \Rightarrow \dfrac{1}{{{f_1}}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{{14}} - \dfrac{1}{\infty }} \right)$
$ \Rightarrow \dfrac{1}{{{f_1}}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{{14}}} \right)$
Solving it
$ \Rightarrow \dfrac{1}{{{f_1}}} = \dfrac{1}{{28}}$
So the focal length of lens 1
$\therefore {f_1} = 28cm$
Similarly we find the focal length of the second lens. For lens 2

Refractive index is ${n_2} = 1.2$
${R_1} = \infty $
${R_2} = - 14cm$ Because ${R_2}$ is in left side of optical canter (by sign convention we take left side distance negative in sign and take right side distance positive )
Apply formula from eq(1)
$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {1.2 - 1} \right)\left( {\dfrac{1}{\infty } - \dfrac{1}{{ - 14}}} \right)$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {1.2 - 1} \right)\left( {\dfrac{1}{{14}}} \right)$
Solving it
$ \Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{1}{{70}}$
So focal length of lens 2
${f_2} = 70cm$

Step 2: In this step we find the focal length of combination of both lenses
We have formula for find equivalent focal length of two lenses is given as
$\dfrac{1}{{{f_{eq}}}} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
Using this formula
 $ \Rightarrow \dfrac{1}{{{f_{eq}}}} = \dfrac{1}{{28}} + \dfrac{1}{{70}}$
Solving it
$ \Rightarrow \dfrac{1}{{{f_{eq}}}} = \dfrac{1}{{20}}$
So the equivalent focal length of these lenses
$\therefore {f_{eq}} = 20cm$
Step 3
Now we can find the distance of image by using lens formula
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Where $u \Rightarrow $ Distance of object
And $v \Rightarrow $ Distance of image
$f \Rightarrow $ Focal length of lens
In question it is given $u = - 40cm$
$f = 20cm$
Simply apply above formula
$ \Rightarrow \dfrac{1}{{20}} = \dfrac{1}{v} - \dfrac{1}{{ - 40}}$
Rearranging it
$ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{20}} - \dfrac{1}{{40}}$
On solving
$ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{40}}$
So the distance of image is
$\therefore v = 40cm$ Right side of lens.

Option (B) is correct here.

Note: Some time we get confuse why some time some distances take positive and some take negative so the answer is we use sign convention to understand sign convention see the diagram

We take all distances positive in the right side of the lens and take negative in the left direction.Similarly, in positive y direction take positive height and in negative y direction take negative.