Question

A body is in limiting equilibrium on a rough plane inclined at ${30^\circ }$ with the horizontal. When the inclination is increased to ${45^\circ }$, the body slides down with acceleration. (Take ${{g}} = 9.8{{m/}}{{{s}}^2}$)

Answer 1

Hint: Drawing the free body diagram of the system will make our work much easier and we can find which forces are acting on the body. As the limiting equilibrium condition is given to us, we can find the coefficient of friction from it, and using it, we can calculate the acceleration of the body.

Formula used:
${{a = }}\dfrac{{{F}}_{net}}{{{m}}} = \dfrac{{{{mg sin}}\theta }}{{{m}}}$
where,${{a}}$ is the acceleration of the body
${{{F}}_{net}}$is the net force acting on the body,
${{m}}$ is the mass of the body,
${{g}}$ is the acceleration due to gravity,
$\theta $ is the angle of inclination.

Complete step by step solution:

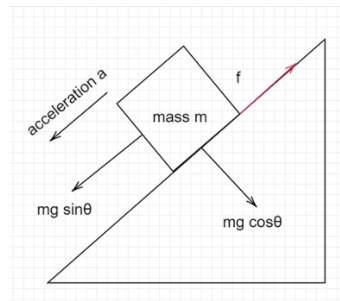
Here,$N$ is the normal force acting by the plank on the body,
$f$ is the frictional force,
$a$ is the acceleration,
$mg\cos \theta $ and $mg\sin \theta $ are the components of the weight of the body.
The gravitational force which is acting in the downward direction is resolved into two components- parallel to the inclined plane and perpendicular to it. The frictional force prevents the body from sliding and its value is which is parallel to the inclined surface and is in the opposite direction of one of the components of gravitational force. Limiting force is the maximum value of static friction and once the body is set in equilibrium, it stops acting on the body.
When $\theta = {60^\circ }$ the body starts to slide down the inclined plane.
According to Newton’s second law of motion:
$\Rightarrow {{a = }}\dfrac{{{F}}_{net}}{m} = \dfrac{{{{mg sin}}\theta }}{{{m}}} = g\sin \theta $
Substituting the given values in the equation we get,
$\Rightarrow a = g(\sin {45^\circ }) = g(\dfrac{1}{{\sqrt 2 }})$
$ \Rightarrow g\dfrac{1}{{\sqrt 2 }} = \dfrac{{9.8}}{{\sqrt 2 }}m/{s^2}$

Note: The frictional force and the normal force are contact forces while the gravitational force is a non-contact force. We should resolve the gravitational force in such directions so that it becomes easier for us, therefore we resolve it along the axis parallel to the inclined planes.