Question

A body weighing ${{0}}{{.4 kg}}$ is whirled in a vertical circle making ${{3 rps}}$. If the radius of the circle is ${{1}}{{.2 m}}$, find the tension in the string at
(i) top of the circle,
(ii) bottom of the circle.

Answer 1

Hint: The best approach to solve these types of questions in which tension is asked, first of all draw a free body diagram. After drawing a free body diagram, write the related equations and then try to solve it. After solving the equation in a simpler form, substitute the given values.

Complete step by step solution:
Given: Mass of the body, ${{m = 0}}{{.4 kg}}$
As the body is making 3 revolutions per second so time period, ${{T = }}\dfrac{{{1}}}{{{3}}}{{ sec}}$
Radius of the circle, ${{r = 1}}{{.2 m}}$
In order to find the tension in the string first we need to calculate angular velocity and the formula of angular velocity is given by
${{\omega = }}\dfrac{{{{2\pi }}}}{{{T}}}$
Now, on substituting the value of time-period in above formula, we get
$
  {{\omega = }}\dfrac{{{{2\pi }}}}{{\dfrac{1}{2}}} \\
  \therefore {{\omega = 4\pi rad }}{{{s}}^{ - 1}} $

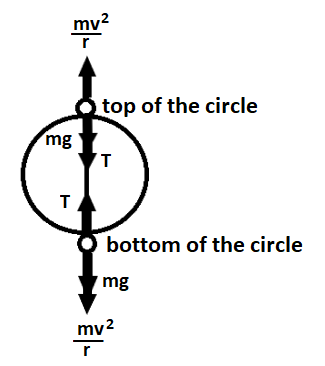
(i) To find the tension in the string at the top of the circle
$\Rightarrow {{T = }}\dfrac{{{{m}}{{{v}}^{{2}}}}}{{{r}}}{{ - mg}}$
The above relation can be written in the form of angular velocity as
$\Rightarrow {{T = mr}}{{{\omega }}^{{2}}}{{ - mg}}$
On taking term “m” common, the above relation can be rewritten as
$\Rightarrow {{T = m(r}}{{{\omega }}^{{2}}}{{ - g)}}$
On substituting the values, we get
\[
\Rightarrow {{T = 0}}{{.4[1}}{{.2 \times (4\pi }}{{{)}}^{{2}}}{{ - 9}}{{.8]}} \\
  \therefore {{T = 71}}{{.8 N}} \]

(ii) To find the tension in the string at the bottom of the circle
$\Rightarrow {{T = }}\dfrac{{{{m}}{{{v}}^{{2}}}}}{{{r}}}{{ + mg}}$
The above relation can be written in the form of angular velocity as
$\Rightarrow {{T = mr}}{{{\omega }}^{{2}}}{{ + mg}}$
On taking term “m” common, the above relation can be rewritten as
$\Rightarrow {{T = m(r}}{{{\omega }}^{{2}}}{{ + g)}}$
On substituting the values, we get
\[
\Rightarrow {{T = 0}}{{.4[1}}{{.2 \times (4\pi }}{{{)}}^{{2}}}{{ + 9}}{{.8]}} \\
  \therefore {{T = 79}}{{.6 N}} \]
Thus, tension in the string at the top of the circle is ${{71}}{{.8 N}}$ and tension in the string at the bottom of the circle is ${{79}}{{.8 N}}$.

Note: The tension force points towards the center of the circle the entire time because tension can only act along the cord which is always a radius of the circle. Therefore in the free body diagram tension always acts towards the center of the circle for both the cases i.e. for top of the circle and for bottom of the circle.