Question

A car is speeding up on a horizontal road with an acceleration $\alpha $. Consider the following situations in the car.
(i) A ball is suspended from the ceiling through a string and is maintaining a constant angle with the vertical. Find this angle.
(ii) A block is kept on a smooth incline and does not slip on the incline. Find the angle of the incline with the horizontal.

Answer 1

Hint: The equations formed by the free body diagram can be used to make equations and by solving these equations we can solve this problem. The constant acceleration of the car will make the suspended ball to make an angle $\theta $ with the vertical.

Complete step by step solution:
(i) It is given in the problem that a bob of mass m is suspended in the car which is accelerating with the acceleration $\alpha $ and we need to find the angle of the bob with vertical.

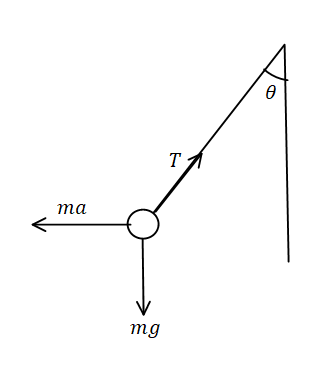
From the above free body diagram.
In the vertical direction,
$ \Rightarrow T\cos \theta = mg$
$ \Rightarrow T = \dfrac{{mg}}{{\cos \theta }}$………eq. (1)
Also,
In the horizontal direction,
$ \Rightarrow T\sin \theta = ma$
$ \Rightarrow T = \dfrac{{ma}}{{\sin \theta }}$………eq. (2)
Equating the tension from equation (1) and equation (2) we get.
$ \Rightarrow \dfrac{{mg}}{{\cos \theta }} = \dfrac{{ma}}{{\sin \theta }}$
$ \Rightarrow \dfrac{g}{{\cos \theta }} = \dfrac{a}{{\sin \theta }}$
$ \Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{a}{g}$
$ \Rightarrow \tan \theta = \dfrac{a}{g}$
$ \Rightarrow \theta = {\tan ^{ - 1}}\dfrac{a}{g}$.

(ii) The angle of the bob with the string which is inside the car makes and angle $\theta $ with the vertical is equal to, $\theta = {\tan ^{ - 1}}\dfrac{a}{g}$.
Now let the angle of the inclination of the inclined plane be $\phi $.

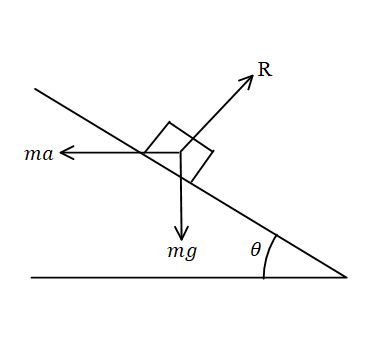
From the above free body diagram,
In the direction perpendicular to the inclined plane.
$ \Rightarrow ma\cos \phi = mg\sin \phi $
$ \Rightarrow a\cos \phi = g\sin \phi $
$ \Rightarrow \dfrac{{\sin \phi }}{{\cos \phi }} = \dfrac{a}{g}$
$ \Rightarrow \tan \phi = \dfrac{a}{g}$
$ \Rightarrow \phi = {\tan ^{ - 1}}\dfrac{a}{g}$
The angle of inclination is given by$\phi = {\tan ^{ - 1}}\dfrac{a}{g}$.

The angle of the bob with vertical which is inside the car is equal to $\theta = {\tan ^{ - 1}}\dfrac{a}{g}$ and the angle of inclination of the smooth inclined plane is equal to $\phi = {\tan ^{ - 1}}\dfrac{a}{g}$.

Note: The bob experiences the forces on the backwards as the response of the acceleration of the car and at the equilibrium position it holds making an angle $\theta $ .The tension in the string always acts away from the body. The acceleration of the car is in the horizontal direction and the weight of the car is in the vertically downward direction.