Question

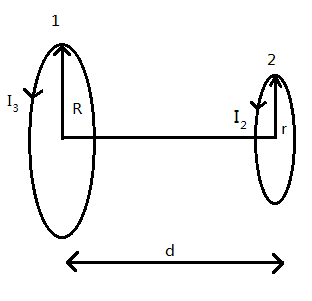
A circular loop of radius $0.3\,cm$ lies parallel to a much bigger circular loop of radius $20\,cm$. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is $15\,cm$ . If a current of $0.2\,A$ flows through the smaller loop, then the flux linked with bigger loop is:

A) $6 \times {10^{ - 11}}\,Wb$
B) $3.3 \times {10^{ - 11}}\,Wb$
C) $6.6 \times {10^{ - 11}}\,Wb$
D) $9.1 \times {10^{ - 11}}\,Wb$

Answer 1

Hint: Flux is the product of a magnetic field with the surface area through which the magnetic field is passing. To calculate the flux linked with the bigger loop, calculate the value of mutual inductance and then multiplying mutual inductance with the current flowing through the bigger loop will give the flux through the bigger loop.

Complete step by step solution:
The given quantities are:
Radius of the smaller loop $r = 0.3\,cm$
Radius of the bigger loop, $R = 20\,cm$ .
Distance between the centre of smaller and bigger loop, $d = 15\,cm$
Current through smaller loop, ${I_2} = 0.2\,A$
Current through bigger loop, ${I_1}$
The magnetic field due to bigger loop ${B_1}$ at any point on the line joining the centres is given as:
${B_1} = \dfrac{{{\mu _0}{I_1}{R^2}}}{{2{{\left( {{d^2} + {R^2}} \right)}^{\dfrac{3}{2}}}}}$
Here, ${\mu _0}$ is a constant having magnitude ${\mu _0} = 4\pi \times {10^{ - 7}}$
Flux linked on the smaller loop ${\Phi _2}$ due to magnetic field ${B_1}$ is given as:
${\Phi _2} = {B_1} \times {A_2}$
Here, ${A_2}$ is the surface area of the smaller loop having value ${A_2} = \pi {r^2}$
Substituting this value in above equation, we get:
${\Phi _2} = \dfrac{{{\mu _0}{I_1}{R^2}}}{{2{{\left( {{d^2} + {R^2}} \right)}^{\dfrac{3}{2}}}}} \times \pi {r^2}$
This is the flux lined to a smaller loop. To calculate the flux linked to a bigger loop, we need to find the value of mutual inductance and then multiply it with the surface area of the bigger loop.
Mutual inductance is the ratio of the flux through a smaller loop produced by the current in a bigger loop. Thus, the mutual inductance ${\rm M}$ will be given as:
${\rm M} = \dfrac{{{\Phi _2}}}{{{I_1}}} = \dfrac{{{\mu _0}{I_1}{R^2}\pi {r^2}}}{{2{{\left( {{d^2} + {R^2}} \right)}^{\dfrac{3}{2}}}}}$
Now, the flux linked with the bigger loop ${\Phi _1}$ will be:
${\Phi _2} = {\rm M}{I_2}$
$ \Rightarrow {\Phi _2} = \dfrac{{{\mu _0}{R^2}\pi {r^2}}}{{2{{\left( {{d^2} + {R^2}} \right)}^{\dfrac{3}{2}}}}} \times {I_2}$
Substituting the given values, we get:
$ \Rightarrow {\Phi _2} = \dfrac{{4\pi \times {{10}^{ - 7}} \times {{\left( {20 \times {{10}^{ - 2}}} \right)}^2} \times \pi \times {{\left( {0.3 \times {{10}^{ - 2}}} \right)}^2}}}{{2{{\left[ {{{\left( {15 \times {{10}^{ - 2}}} \right)}^2} + {{\left( {20 \times {{10}^{ - 2}}} \right)}^2}} \right]}^{\dfrac{3}{2}}}}} \times 2$
Solving this we get:
$ \Rightarrow {\Phi _2} = 9.1 \times 1{0^{ - 11}}\,weber$
The flux linked with the bigger loop is of $9.1 \times 1{0^{ - 11}}$ $weber$.

Thus, option D is the correct option.

Note: Mutual inductance is the ratio of flux linked in one loop to the current flowing in another loop. Flux can be calculated as a product of magnetic fields in one loop with the surface area of another loop or magnetic flux is product of the mutual inductance with the current flowing in the other loop. The unit of flux is weber and it is denoted as $Wb$.