Question

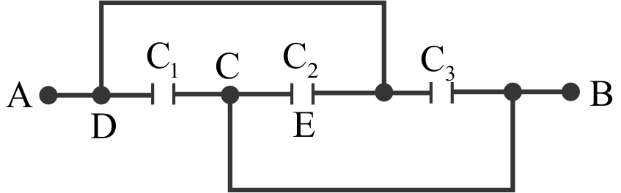
A combination of parallel plate capacitors is maintained at a certain potential difference. When a $3mm$ thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between the plates is increased by $2.4mm$. Find the dielectric constant of the slab.
      
A. $4$
B. $5$
C. $3$
D. $6$

Answer 1

Hint Find the equivalent capacitance both with and without the slab between the plates and equate them. Use suitable formula to establish the expression for capacitance.
Formulas used:
$C={\displaystyle \frac{{\epsilon }_{0}A}{d}}$ where $d$ is the distance between the capacitance plates, $A$ is the area of the plates and ${\epsilon }_0$ is the permittivity of free space.
$C^{\prime }={\displaystyle \frac{{\epsilon }_{0}A}{d^{\prime }-t\left(1-{\displaystyle \frac{1}{K}}\right)}}$ where $K$ is the relative permittivity of the material of the slab and $d^{\prime }$is the distance between the capacitor plates, $t$ is the thickness of the slab introduced.

Complete step by step answer
A capacitor is a system of conductors and dielectric that can store electric charge. It consists of two conductors containing equal and opposite charges and has a potential difference $V$ between them.
The potential difference between the conductors is proportional to the charge on the capacitor and is given by the relation $Q=CV$where $Q$ is the charge on the positive conductor and $C$ is called the capacitance.
Now, we know that the potential difference between the two plates is given by, $V=E\times d$ where $d$ is the distance between the two plates.
Thus, substituting the value of $V$ in the equation$Q=CV$, we get,
$Q=CEd$
Putting $E={\displaystyle \frac{\sigma }{{\epsilon }_0}}$ and $\sigma ={\displaystyle \frac{Q}{A}}$ where $A$ is the area of the capacitor plate, we get
$Q=C\times {\displaystyle \frac{Q}{A{\epsilon }_0}}\times d$
$\Rightarrow C={\displaystyle \frac{A{\epsilon }_0}{d}}$ where $C$ be the equivalent capacitance between terminals A and B.
Now, introducing a slab of thickness $t$, the resultant capacitance $C^{\prime }$ becomes
$C^{\prime }={\displaystyle \frac{{\epsilon }_{0}A}{d^{\prime }-t\left(1-{\displaystyle \frac{1}{K}}\right)}}$ where $K$ is the relative permittivity of the material of the slab and $d^{\prime }$is the new distance between the capacitor plates.
Now, since the potential difference remains same, the capacitance must also not vary
So, $C=C^{\prime }$
$\Rightarrow {\displaystyle \frac{A{\epsilon }_0}{d}}={\displaystyle \frac{A{\epsilon }_0}{d^{\prime }-t\left(1-{\displaystyle \frac{1}{K}}\right)}}$
$$\begin{gathered} \Rightarrow d=d^{\prime }-t\left(1-{\displaystyle \frac{1}{K}}\right) \\ \Rightarrow d=d+2.4-3\left(1-{\displaystyle \frac{1}{K}}\right) \\ \Rightarrow 2.4-3+{\displaystyle \frac{3}{K}}=0 \\ \Rightarrow {\displaystyle \frac{3}{K}}=0.6 \\ \Rightarrow K=5 \end{gathered}$$

Therefore, the correct option is B.

Note:To establish the capacitance of an isolated single conductor, we assume the conductor to be a part of a capacitor whose other conductor is at infinity.