Question

A heavy block of mass $M$ hangs in equilibrium at the end of a rope of mass $m$ and length $l$ connected to a ceiling. Determine the tension in the rope at a distance $x$ from the ceiling.

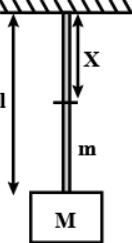
(A) $Mg + mg\left( {\dfrac{{l - x}}{x}} \right)$
(B) $Mg + mg\left( {\dfrac{{l - x}}{l}} \right)$
(C) $mg + Mg\left( {\dfrac{{l - x}}{l}} \right)$
(D) $mg + Mg\left( {\dfrac{{l - x}}{x}} \right)$

Answer 1

Hint To find the tension in the rope at a distance $x$ from the ceiling, you need to find the net mass that is being supported by the rope, taking the contribution only up to that particular point which is $x$ distance below the ceiling. Once you find the net mass that is being supported, simply equate the forces to find the answer.

Complete step by step answer
We will proceed with the solution exactly as explained in the hint section of the solution to the question. We will find the net mass that is being supported by the rope, taking the contribution only up to that particular point which is $x$ distance below the ceiling. To do that, let’s have a look at what is given to us in the question:
The mass of the box is given us to be $M$
The mass of the rope itself is $m$
The length of the rope is $l$
Since no information is given about the distribution of the mass of the rope, we can take it to be uniform, and thus, we can define the mass density of the rope as:
$\lambda = \dfrac{m}{l}$
Now, let’s have a look at the image given in the question:

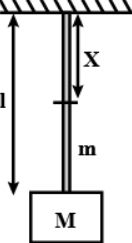
Here, we can see that if the point is $x$ distance below the ceiling, the mass that it supports is not only of the box, but of the remaining rope too, whose length is clearly seen as:
$l' = l - x$
Now, we can see that the weight that is supports is as follows:
$w = Mg + \lambda l'g$
We already know the value of $\lambda $ and $l'$ . Substituting them in the equation above, we get:
$w = Mg + \dfrac{m}{l}\left( {l - x} \right)g$
Now, if we equate the forces at the point, we can see that:
$T = Mg + mg\left( {\dfrac{{l - x}}{l}} \right)$
Where, $T$ is the tension in the rope at a distance $x$ below the ceiling.

Hence, we can see that the option (B) is the correct option as the value matches with the value that we just found out.

Note The main concept or step where majority of the students get stuck is at the step where we justify the taking of rope’s mass density as uniform, since without the rope’s mass density being uniform, the question gets more complex and needs more information which is not provided in the question. Hence, remember that if no information is given, we can take the mass density as uniform.