Question

A man can swim with velocity $v$ relative to water. He has to cross the river of width $d$ flowing with the velocity $u(u > v)$ . The distance through which he carried downstream by the river is $x$ . Which of the following is correct?
A. If he crosses the river in minimum time, $x = \dfrac{{dv}}{v}$
B. $x$ cannot be less than $\dfrac{{du}}{v}$
C. For $x$ to be minimum he has to swim in the direction making an angle of $\dfrac{\pi }{2} + {\sin ^{ - 1}}\left( {\dfrac{v}{u}} \right)$ with the direction of flow of water.
D. $x$ will be max if he swims in the direction of making an angle of $\dfrac{\pi }{2} + {\sin ^{ - 1}}\left( {\dfrac{v}{u}} \right)$ with the direction of flow of water.

Answer 1

Hint: - We will simply use $speed = \dfrac{{dis\tan ce}}{{time}}$ along with some geometry. In order to find the maximum and minimum of the particular quantity we will put slope equal to zero.

Complete step by step answer:

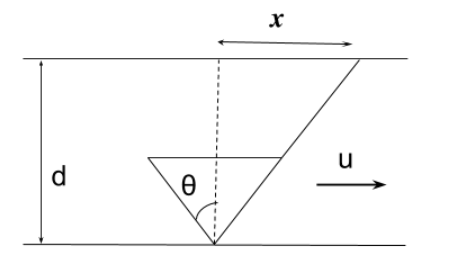
Given: Velocity of man relative to water $ = v$
Width of river $ = d$
Velocity of river $ = u$
Now, time required for crossing the river is given by
$\Rightarrow$ $t = \dfrac{d}{{{v_{parallel}}}}$
From figure, ${v_{parallel}} = v\cos \theta $ and ${v_{perpendicular}} = v\sin \theta $
$\therefore t = \dfrac{d}{{v\cos \theta }} \cdots \left( 1 \right)$
For the time to be minimum, $\theta $ should be zero
$\Rightarrow$ $t = \dfrac{d}{{v\cos 0}} = \dfrac{d}{v}$
Now, $x = $ horizontal velocity $ \times $ time
$\Rightarrow$ $x = \left( {u - v\sin \theta } \right) \times \dfrac{d}{{\cos \theta }}$
For minimum time,
$
  x = \left( {u - v\sin 0} \right)\dfrac{d}{v} \\
  x = \dfrac{{du}}{v} \\
 $
From above,
\[
  x = (u - v\sin \theta ) \times \dfrac{d}{{v\cos \theta }} \\
  x = \dfrac{{ud\sec \theta }}{v} - d\tan \theta \\
 \]
For $x$ to be minimum,
$\dfrac{{dx}}{{d\theta }} = 0$
That is,
 $
  \dfrac{{d\left[ {u\dfrac{d}{v}\sec \theta - d\tan \theta } \right]}}{{d\theta }} = 0 \\
   \Rightarrow \dfrac{{ud}}{v} \times \sec \theta \tan \theta - d{\sec ^2}\theta = 0 \\
   \Rightarrow \dfrac{u}{v}\tan \theta - \sec \theta = 0 \\
  \dfrac{{u\sin \theta }}{{v\cos \theta }} = \dfrac{1}{{\cos \theta }} \\
  \sin \theta = \dfrac{v}{u} \\
  \theta = {\sin ^{ - 1}}\left( {\dfrac{v}{u}} \right) \\
 $
The swimmer has to swim in the direction making an angle of $\dfrac{\pi }{2} + {\sin ^{ - 1}}\left( {\dfrac{v}{u}} \right)$ with the direction of flow of water.

Hence, option (A) and (C) are correct.

Note: - Since, in the question, $(u > v)$ hence, we have to add $\dfrac{\pi }{2}$ . If $v > u$ then, $\dfrac{\pi }{2}$ will be subtracted. Hence, for $x$ to be minimum, the swimmer has to swim in a particular direction with the direction of flow of water.