Question

A man is 180cm tall and his eyes are 10cm below the top of his head. In order to see his entire height right from toe to head, he uses plane mirror kept at a distance of 1m from him, The minimum length of the plane mirror required is:
(A) 180cm
(B) 90cm
(C) 85cm
(D) 170cm

Answer 1

Hint: First of all make a diagram for the given situation then think about what is the must condition to see the full image of its own body. If you notice hard you will find that the height of the mirror will be independent of its distance from the body. And there is a simple relation, you can also generalize the result for any case.

Complete step-by-step answer:
For any person to see its full image in a mirror the following conditions must satisfy.
Suppose he is seeing his head then from the first property of reflection i.e. angle of incidence is equal to the angle of reflection we will find that the top of the mirror should be placed at exactly middle of the eyes and head. And the same case occurs when you want to see your toe.
See the following figure to understand the concept clearly: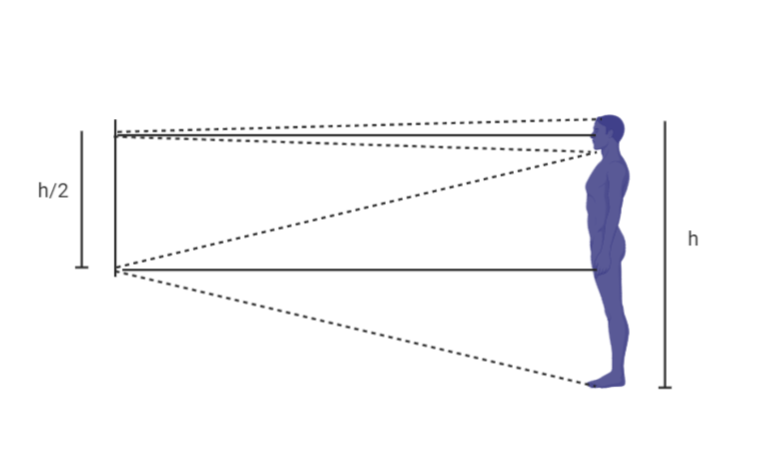

So here we observe that the mirror must be at least half of the height of the body to see its full image in the mirror.
Therefore,
\[{H_{mirror}} = \dfrac{{{H_{body}}}}{2}\]
\[{H_{mirror}} = \dfrac{{180}}{2}\]
\[{H_{mirror}} = 90cm\]

Hence option B is correct.

Note: So here we have generalized equation: \[{H_{mirror}} = \dfrac{{{H_{body}}}}{2}\] to calculate the height of the mirror whenever you are the height of body. You can even observe the same phenomena at your home with a wall mirror and the same experiment hand mirror. In vehicles convex mirrors are used so that is a different case in which you see big images in such a small mirror.