
A particle is given an initial speed
A)
B)
C)
D)
Answer
142.8k+ views
Hint: To solve this question, we have to calculate the resultant of the tangential and centripetal acceleration. We all know the value of tangential acceleration which is equal to the value of acceleration due to gravity. The centripetal acceleration can be calculated by using velocity and the radius of the circle.
Formulae used:
Here
Here
Complete step by step solution:
We know that in a circle the velocity at the lowest most position will be,
Here
So,
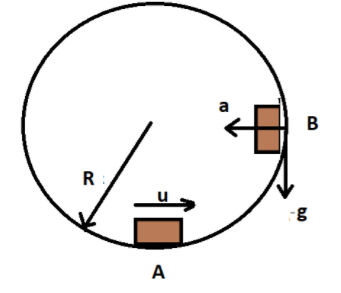
Applying conservation of energy at points A and B, we get
Here
The negative sign in gravity is because of its downwards action.
Simplifying the equation, we get,
Putting the value of
So the value of tangential velocity at point B is
We know that,
Here
Putting the values of
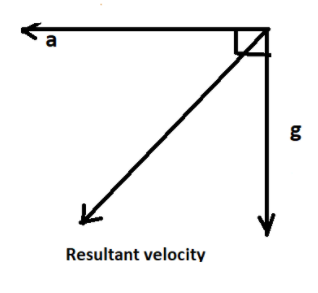
From the above diagram, the resultant acceleration acting on the body will be,
Putting the value of
So the net acceleration acting on the body will be
Hence option (A) is the correct option.
Note: In a vertical circle,
1. The velocity at the lower most position is
2. The velocity at the horizontal position is
3. The velocity at the top most position is
Here
Formulae used:
Here
Here
Complete step by step solution:
We know that in a circle the velocity at the lowest most position will be,
Here
So,

Applying conservation of energy at points A and B, we get
Here
The negative sign in gravity is because of its downwards action.
Simplifying the equation, we get,
Putting the value of
So the value of tangential velocity at point B is
We know that,
Here
Putting the values of

From the above diagram, the resultant acceleration acting on the body will be,
Putting the value of
So the net acceleration acting on the body will be
Hence option (A) is the correct option.
Note: In a vertical circle,
1. The velocity at the lower most position is
2. The velocity at the horizontal position is
3. The velocity at the top most position is
Here
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
EMI starts from ₹2,775 per month
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Degree of Dissociation and Its Formula With Solved Example for JEE

Physics Average Value and RMS Value JEE Main 2025

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




