Question

A particle is projected at an angle of elevation $\alpha $ and after $t$ seconds it appears to have an elevation of $\beta $ as seen from the point of projection. Find the initial velocity of projection.

Answer 1

Hint: In this question, draw the diagram as per the given situation and then calculate the height and the horizontal distance travel by the particle by using the equation of motion. Then find the velocity at $x,y$- axis as it is the value of height and vertical distance traveled by particle when it is projected. Thus calculate the initial velocity from all the data.

Complete step by step answer:
As per the question, it is given that a particle is projected at an angle of elevation $\alpha $ and after $t$ seconds it appears to have an elevation of $\beta $.
Now, we will draw the diagram as per the given conditions as,

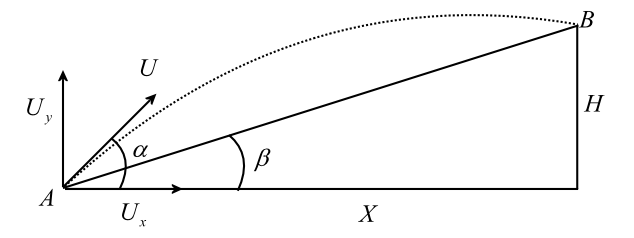
Let us consider a particle is projected at a velocity $U$ and after $t$ seconds it reaches point $B$. Initially the angle of elevation was $\alpha $ and after $t$ second angle of elevation is $\beta $. The horizontal distance travel by the particle is $X$. In the subscript, $x$ denotes the properties in $x$ direction and $y$ denotes the properties in $y$ direction.
As we know that, the formula for the height in case of projectile motion is,
$H = {U_y} + \dfrac{1}{2}{a_y}{t^2}$
Where, ${U_y}$ is velocity along the $y$-axis which is equal to $U\sin \alpha $ and the acceleration along the $y$ axis is ${a_y}$ which is equal to $ - g$.
By substituting the values in the above equation, we get,
$U\sin \left( \alpha \right) \times t + \dfrac{1}{2} \times \left( { - g} \right){t^2} = U\left( {\sin \alpha } \right)t - \dfrac{1}{2}g{t^2}$
As we know that the horizontal velocity can be written as,
${U_x} = U\left( {\cos \alpha } \right)$
Where ${U_x}$is velocity at$x$-axis].
Now, we calculate the horizontal distance travel by the particle as
$X = {U_x}t$
By substituting the given values as,
$X = U\left( {\cos \alpha } \right)t$
Now, by using the above diagram, we calculate the angle of elevation as,
$\tan \beta = \dfrac{H}{X}$
Put the value of$H$and$X$in the above equation.
\[ \Rightarrow \tan \beta = \dfrac{{U\left( {\sin \alpha } \right)t - \dfrac{{g{t^2}}}{2}}}{{U\left( {\cos \alpha } \right)t}}\]
By using cross-multiplication, we get,
\[ \Rightarrow U\left( {\cos \alpha } \right)t.\tan \beta = U\left( {\sin \alpha } \right)t - \dfrac{{g{t^2}}}{2}\]

By simplification we obtain the expression of the velocity as,

\[ \Rightarrow U = \dfrac{{gt}}{{2\left[ {\sin \alpha - \cos \alpha .\tan \beta } \right]}}\]

$\therefore $ When the particle is projected at an elevation angle of $\alpha $ the initial velocity was $U = \dfrac{{gt}}{{2\left[ {\sin \alpha - \cos \alpha .\tan \beta } \right]}}$.


Note: As we know that the sign of acceleration due to gravity will be taken as negative if the body or particle is moving upward because gravity tries to accelerate the body and if the body moves downward then it will be positive because gravity tries to accelerate the particle of the body.