Question

A plano-convex lens of refractive index 1.5 and radius of curvature 30cm is silvered at the curved surface. Now this lens has been used to form the image of an object. At what distance from this lens, an object has to be placed in order to have a real image of the size of the object?
A) 20cm
B) 30cm
C) 60cm
D) 80cm

Answer 1

Hint: When the curved side of the plano-convex lens is silvered, when it is viewed from the other end, it behaves like a concave mirror. Hence, we have to apply the rules of reflection on a concave mirror.

Complete step by step answer:
A plano-convex lens consists of two faces joined together, with one face straight and the other face bulged outward as shown:

If the bulged part of the lens is coated with silver, the plano-convex lens behaves as a concave mirror with the inner surface acting as the reflecting surface.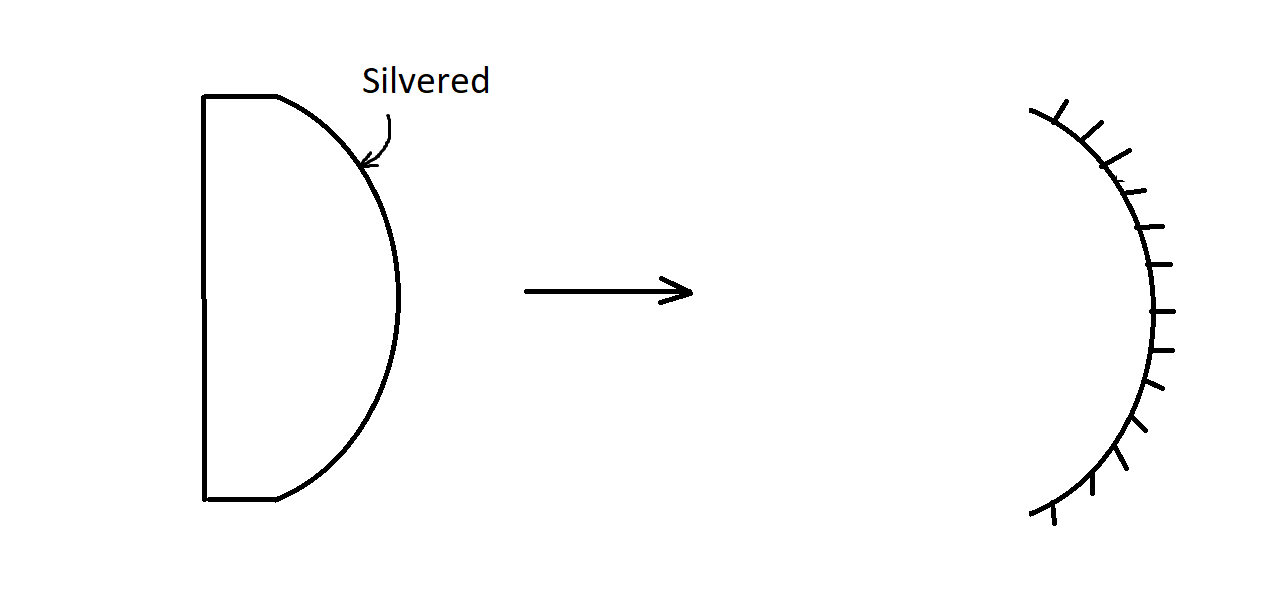
The radius of curvature of the curved surface, $R = 30cm$
Let us consider an object placed at the centre of curvature of the mirror as shown:

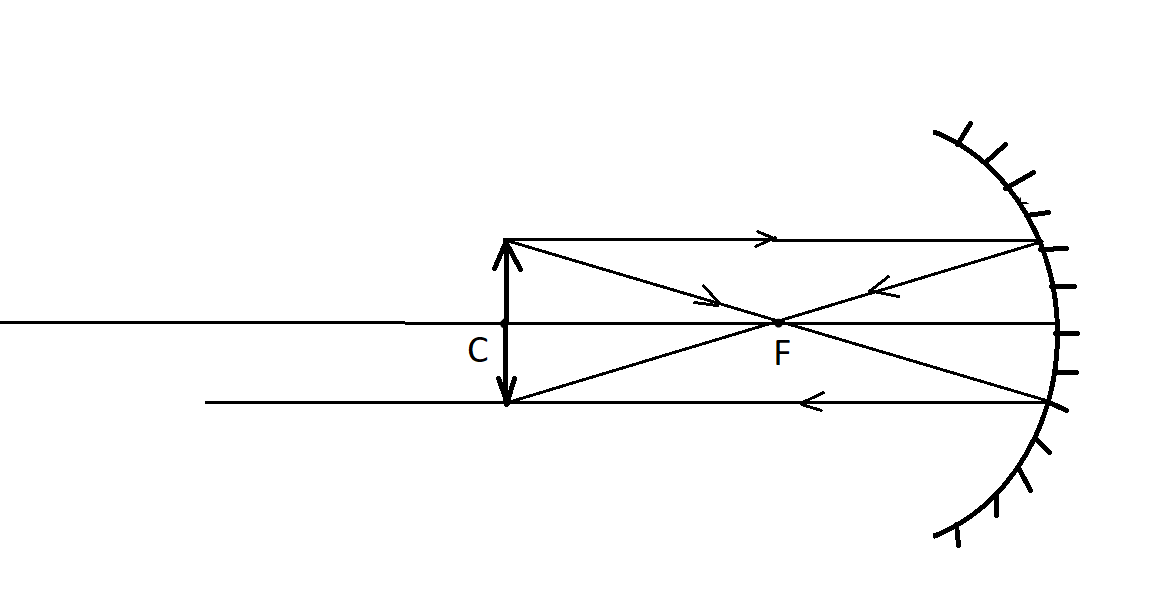
There are two rays emerging out of the object.
i) The first ray passes through the principal focus F and after reflection, passes parallel to the principal axis.
ii) The second ray passes parallel to the principal axis and after reflection, passes through the principal focus F.
The two rays meet and form an image at the centre of curvature, C.
The image formed is of the same size as that of the object and hence, the magnification is unity as there is no increase or decrease in the size of the object.
Hence, to produce a real image of the size of the object after reflection, the object must be placed at the centre of curvature of the mirror.
Here, the radius of curvature of the mirror is equal to $R = 30cm$.

Hence, the correct option is Option B.

Note: The radius of curvature of the mirror has the negative sign since the radius of curvature of a concave mirror and lens is always negative. Here, we have considered the magnitude of the radius of curvature. The actual designation of the radius of curvature, $R = - 30cm$.