Question

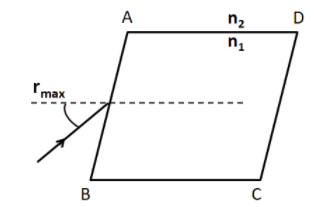
A rectangular glass slab ABCD of refractive index \[{n_1}\] is immersed in water of refractive index ${n_2}$ $\left( {{n_1} > {n_2}} \right)$. A ray of light is incident to the surface AB of the slab as shown. The maximum value of the angle of incidence ${r_{\max }}$ such that the ray comes out only from the another surface CD is given by

(A) ${\sin ^{ - 1}}\left[ {\dfrac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\left( {\dfrac{{{n_1}}}{{{n_2}}}} \right)} \right)} \right]$
(B) ${\sin ^{ - 1}}\left[ {{n_1}\cos \left( {{{\sin }^{ - 1}}\left( {\dfrac{1}{2}} \right)} \right)} \right]$
(C) \[{\sin ^{ - 1}}\left( {\dfrac{{{n_1}}}{{{n_2}}}} \right)\]
(D) \[{\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)\]

Answer 1

Hint: To solve this question, we need to apply the concept of total internal reflection within the glass slab. Then applying the Snell’s law at the interface AB we will get the answer.

Complete step-by-step solution:
For emerging out of the face CD of the slab, the angle of incidence should be such that the refracted ray suffers total internal reflection within the rectangular slab. As it will suffer multiple total internal reflections within the slab, it will reach the face CD and get refracted out of the slab.
We know that for total internal reflection to occur, the light ray must be incident at an angle greater or equal to the critical angle of incidence.
For the maximum angle ${r_{\max }}$, the ray will be incident at the critical angle of incidence.
Consider the following figure

In the triangle FED we have
$r + {i_c} = {90^ \circ }$
$ \Rightarrow r = {90^ \circ } - {i_c}$.................(1)
Applying Snell’s law at the interface AB, we have
\[{n_2}\sin {r_{\max }} = {n_1}\sin r\]
Putting (1) in above equation, we get
\[{n_2}\sin {r_{\max }} = {n_1}\sin \left( {{{90}^ \circ } - {i_c}} \right)\]
\[ \Rightarrow {n_2}\sin {r_{\max }} = {n_1}\cos {i_c}\].................(2)
Now, we know that the critical angle of incidence is equal to the sine inverse of the reciprocal of the refractive index of denser medium with respect to the rarer medium. So we have
${i_c} = {\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)$...........(3)
Putting (3) in (2) we get
\[{n_2}\sin {r_{\max }} = {n_1}\cos \left[ {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]\]
\[ \Rightarrow \sin {r_{\max }} = \dfrac{{{n_1}}}{{{n_2}}}\cos \left[ {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right]\]
Taking sine inverse both the sides, we get
\[{r_{\max }} = {\sin ^{ - 1}}\left[ {\dfrac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)} \right)} \right]\]

Hence, the correct answer is option A.

Note: The phenomena of total internal reflection to get the light ray, which was incident on one face, transmitted to the opposite face is used in the optical fibre cables. The angle of incidence, which was ${r_{\max }}$ here, is known as the acceptance angle.