Question

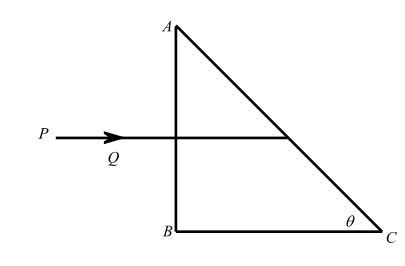
A right-angled prism made from a material of refractive index $\mu $ is kept in air. A ray PQ is incident normally on the side AB of the prism. Find (in terms of $\mu $ ) the maximum value of $\theta $ up to which this incident ray necessarily undergoes total internal reflection at the face AC of the prism.

Answer 1

Hint:In this question, we know that if the angle between two lines is the same as the angle between their perpendiculars and one angle of right angles prism is always $90^\circ $. The angle of incidence should be minimum for total internal reflection.

Complete step by step solution:
In this question we have given that a right-angled prism has the refractive index $\mu $. We need to calculate the maximum value of $\theta $ up to which this incident ray necessarily undergoes total internal reflection at the face AC of the prism.

In this question let us assume that the angle of incidence is $i$ and the angle of incidence is incident on $AC$.
The angle between two lines is same as the angle between their perpendiculars so we can write,
$i = A$
Since the prism is right angled, we can write,
\[ \Rightarrow \theta = \dfrac{\pi }{2} - A\]
Since $i = A$ we can write,
$ \Rightarrow \theta = \dfrac{\pi }{2} - i......\left( 1 \right)$
We know that refractive index is expressed as,
$\mu = \dfrac{1}{{\sin i}}$
As we know that the angle of incidence should be minimum for the total internal reflection,
${i_c} = {\sin ^{ - 1}}\dfrac{1}{\mu }......\left( 2 \right)$
Here, ${i_c}$ is a critical angle.

Now the maximum value of $\theta $ for total internal expression can be calculated by substituting the expression of ${i_c}$ to the equation (1) as,
$ \Rightarrow \theta = \dfrac{\pi }{2} - {i_C}$

Now we substitute the value of critical angle as expressed in equation (2) in above equation to get the maximum value of $\theta $.
$\therefore {\theta _{\max }} = \dfrac{\pi }{2} - {\sin ^{ - 1}}\dfrac{1}{\mu }$

Therefore, the maximum value will be ${\theta _{\max }} = \dfrac{\pi }{2} - {\sin ^{ - 1}}\dfrac{1}{\mu }$.

Note:As we know that the minimum angle for total internal reflection is the critical angle. The angle of the right-angled prism is $90^\circ $. The maximum value of $\theta $ is calculated corresponding to the minimum value of $i$.