Question

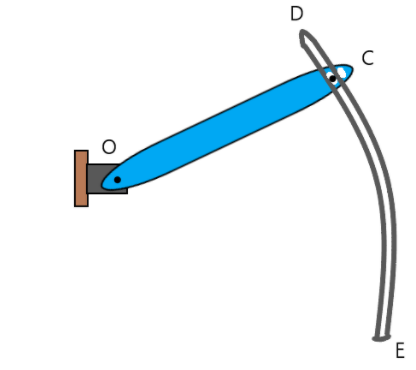
A small 2 kg ball can move freely with no friction along the circular path DE of radius 120 cm and on linear path along the rotating arm OC. If at a given instant \[\theta = 0.3rad\], \[\dot \theta = 6\dfrac{{rad}}{s}\] and \[\ddot \theta = 66rad/{s^2}\], determine (a) the radial and transverse components of the resultant force, (b) the forces exerted on the ball by the arm OC and the wall of the circular slot DE.

Answer 1

Hint: radial component of the force can be gotten from the centripetal acceleration of the ball. The transverse component of the force can be derived from the tangential acceleration of the ball.
Formula used: In this solution we will be using the following formulae;
\[{a_c} = {\dot \theta ^2}R\] where \[{a_c}\] is the centripetal acceleration of a body circulating about a point, \[\dot \theta \] is the angular velocity of the body, and \[R\] is the radius of the circular path.
\[{a_t} = \ddot \theta R\] where \[{a_t}\] is the tangential or transverse acceleration of a circulating body, and \[\ddot \theta \] is the angular acceleration of the body.
\[F = ma\] where \[F\] is force exerted on a body, \[m\] is mass, and \[a\] acceleration of a body

Complete Step-by-Step solution:
To find the centripetal force, we shall first calculate the centripetal acceleration of the ball, at the given instant.
The centripetal acceleration can be given by
\[{a_c} = {\dot \theta ^2}R\] where \[\dot \theta \] is the angular velocity and \[R\] is the radius of the circle
Hence, by inserting known values, we have
\[{a_c} = {6^2}\left( {1.2} \right)\] (since 120 cm is \[1.2m\])
\[ \Rightarrow {a_c} = 43.2m/{s^2}\]
Hence, from newton’s second law, the centripetal force can be given as
\[F = m{a_c}\]where\[m\] is the mass of the body, hence for our ball, we have
\[F = \left( {2 \times 43.2} \right) = 86.4N\]
For the transverse force, we calculate the tangential acceleration which can be given by
\[{a_t} = \ddot \theta R\]where\[\ddot \theta \] is the angular acceleration of the body.
Inserting values from question, we have
\[{a_t} = \left( {66} \right)1.2 = 79.2m/{s^2}\]
Then the transverse force on the ball will be
\[F = m{a_t} = 2 \times 79.2\]
\[ \Rightarrow F = 158.4N\]
For part b)
The force exerted by the arm OC is transverse, and the force by DE is radial.

Note: for clarity, the force exerted by the arm OC is transverse because this is the part which hits the ball in linear motion, while the arm DE prevents it from going in linear motion but keeping around a circular path in the shape of itself.