Question

A sphere, a cube, and a thin circular disc, all made of the same material, have some mass. Their initial temperature is$3 \times {10^3}^\circ C$. The body which cools rapidly is:
(A) Sphere
(B) Cube
(C) Both sphere and cube
(D) Circular plate

Answer 1

Hint Given that all the objects are of the same materials and having the same mass also and are heated at the same temperature. This problem can be solved by first understanding the dimensions of the objects. We will find the rate of cooling by using Newton’s law of cooling which provides information about which body will cool faster.
Formula used
Newton’s law of cooling
$ \Rightarrow \dfrac{{dQ}}{{dt}} = mC\dfrac{{\Delta T}}{{dt}}$
where $\dfrac{{dQ}}{{dt}}$ is the rate of radiation
$m$= mass
$C$= specific heat
 $\dfrac{{\Delta T}}{{dt}}$ = rate of temperature change.

Complete Step by step solution
We will start by understanding the properties of dimensions of the objects. Here, given that cube, sphere, and circular disc or plate have the same mass and are made of the same materials and also their initial temperature is also the same.

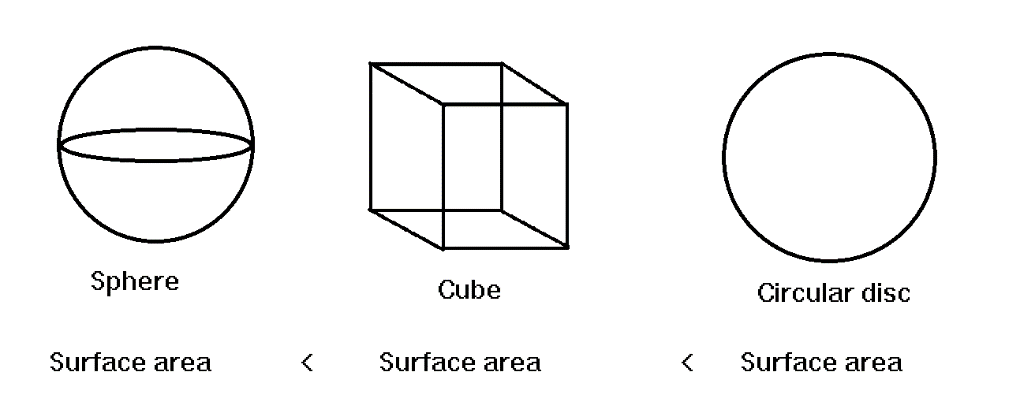
But if we discuss the surface then we can see that the surface area of the disc is more than the cube and the surface area of the cube is more than the sphere.
Now from Newton’s law of cooling, we can deduce that
$\dfrac{{dQ}}{{dt}} = mC\dfrac{{\Delta T}}{{dt}}$ ---------------- Equation $(1)$
where $\dfrac{{dQ}}{{dt}}$ is the rate of radiation
$m$= mass
$C$= specific heat
 $\dfrac{{\Delta T}}{{dt}}$ = rate of change in temperature
Also rearranging the above Equation $(1)$ we can rewrite it as
$\dfrac{{\Delta T}}{{dt}} = \dfrac{{dQ}}{{dt}}\dfrac{1}{{mC}}$
Now from Stefan-Boltzmann law, we know that the heat energy radiation can be given as
$Q = e\sigma A({T^4} - T_0^4)$ ------------- Equation $(2)$
where $e$= emissivity
$T$= Temperature of an object
${T_0}$= Temperature of surroundings
$\sigma $= Stefan’s constant
$A$= surface area
Now substituting the Equation $(2)$in Equation $(1)$ we get
$\dfrac{{\Delta T}}{{dt}} = \dfrac{{e\sigma A({T^4} - T_0^4)}}{{mC}}$
As it is given that the mass is the same for all the object hence
${m_{sphere}} = {m_{cube}} = {m_{disc}}$
Also, all other quantities like emissivity$e$, Stefan’s constant$\sigma $, and initial temperature which is $3 \times {10^3}^\circ C$ but the surface area $A$ of all the given objects are different.
Hence the rate of cooling is directly proportional to the surface area of the substance or object.
$\therefore \dfrac{{\Delta T}}{{dt}} \propto A$
We know that
$ \Rightarrow {A_{sphere}} < {A_{cube}} < {A_{disc}}$
Therefore as the surface area of the circular disc is larger than the cube and sphere hence it will need less time to cool which means the heat will dissipate more.

Hence option (D) is the correct answer.

Note Here we have used another law that is Stefan-Boltzmann law which states that total heat that is radiated from any surface of an object is proportional to the fourth power of the absolute temperature of that object. It gives$Q \propto {T^4}$.