Question

A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass and coefficient of restitution (e). The ratio of the velocities of the two spheres after collision will be:

A) \[\dfrac{{1 - e}}{{1 + e}}\]
B) \[\dfrac{e}{{e + 1}}\]
C) \[\dfrac{2}{e}\]
D) \[\dfrac{{e + 1}}{{2e}}\]

Answer 1

Hint: Coefficient of restitution is used whenever there is a collision between two particles or bodies. Coefficient of restitution determines the type of collision whether it is elastic or not. This is done so as to know if there is any loss of kinetic energy after collision or not. It is the ratio of final to initial relative velocity between two bodies after collision.
Given that two particles are made to collide with each other so they must be possessing some momentum. Since momentum is related to speed, mass, direction and force required to keep objects moving or to stop them. Law of conservation of momentum states that momentum of a system remains unchanged. It can be transformed from one form to another but it can not be destroyed or created.

Complete step by step solution:
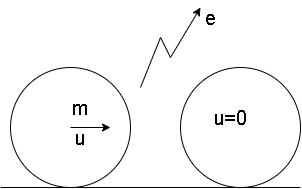
Since mass of both the spheres is same \[{m_1} = {m_2} = m\]
Let \[{u_1} = u\]and \[{u_2} = 0\]be their velocities before collision
Let \[{v_1},{v_2}\]be their momentum after collision.
According to Principle of Conservation of momentum
\[{m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1} + {m_2}{v_2}\]
Substituting all the values and solving,
\[\Rightarrow mu + m(0) = m{v_1} + m{v_2}\]
\[\Rightarrow mu = m({v_1} + {v_2})\]
\[\Rightarrow u = {v_1} + {v_2}\]……(i)
By definition of coefficient of restitution
\[\Rightarrow e = \dfrac{{{v_2} - {v_1}}}{{u - 0}}\]
\[\Rightarrow {v_2} - {v_1} = eu\]……(ii)
From equation (i) and (ii)\[\]
\[\Rightarrow {v_1} + {v_2} = u\]
\[\Rightarrow {v_1} - {v_2} = eu\]
Solving above equations and evaluating values,
\[\Rightarrow {v_1} = \dfrac{{(1 - e)u}}{2}\]……(iii)
\[\Rightarrow {v_2} = \dfrac{{(1 + e)u}}{2}\]……(iv)
Dividing (iii) and (iv),
\[\Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{1 - e}}{{1 + e}}\]
Option A is the correct answer.

Note: Momentum is used in everyday life, so it has its own significance. One of the examples is the air bags these days in cars are made taking care of protection from injury to the passengers. Because airbags increase the time required to stop momentum of driver and passenger and minimizes the effect of force on an object or person due to collision.