Question

A spring, which is initially in its unstretched condition, is first stretched by a length $\left( x \right)$ and then again by a further length $\left( x \right)$. The work is done in the first case ${W_1}$​ and the second case ${W_2}$​. Find $\left( {\dfrac{{{W_1}}}{{{W_2}}}} \right)$.

Answer 1

Hint: Initially, when spring is at an unstretched position its potential energy is zero. Now, as the spring is stretched as we are working against the rest position of spring and as we stretch it tends to go to its initial shape due to this it gains potential energy. So, work done to stretch spring is equal to the potential energy gained by the spring.

Complete step by step solution:
Refer to the following diagram

Here we can see the unstretched spring and here it is at rest no restoring force is acting so no potential energy
Spring is stretched to a length $\left( x \right)$

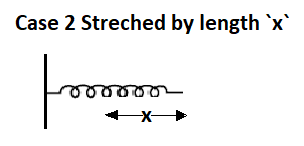
Now as the initial rest position of spring is disturbed and it is stretched by a length $\left( X \right)$ a restoring force comes into play to oppose the force applied for stretching, as we hold the spring stretched it will acquire potential energy, so we can say that the work done to stretch spring is equal to change in its potential energy
$W = \Delta P.E$
So, work done will be \[{W_{}} = \dfrac{1}{2}k{\left( {X - {x_o}} \right)^2}\]
Where
$\left( k \right)$ is the spring constant
$\left( {{x_0}} \right)$is the initial position
$\left( X \right)$distance stretched
Therefore in this case the work done $\left( {{W_1}} \right)$ will be
\[{W_1} = \dfrac{1}{2}k{\left( {X - {x_o}} \right)^2}\]
Here,
${x_o} = 0$
$X = x$
So, \[{W_1} = \dfrac{1}{2}k{x^2}\]
Now,
When Spring is again stretched by length $\left( X \right)$

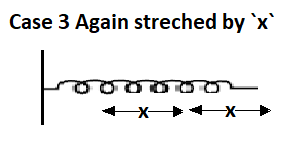
Here as we can see that spring is stretched again by $\left( X \right)$
So, initially, it was stretched by and now $\left( X \right)$ again by $\left( X \right)$ so total stretch length becomes $X + X = 2X$
Now as again spring is stretched so its potential energy will again be increased
As \[{W_{}} = \dfrac{1}{2}k{\left( {X - {x_o}} \right)^2}\]
Here, $
  X = 2x \\
\Rightarrow {x_o} = x \\
 $
So, Work done $\left( {{W_2}} \right)$ for this stretching will be
\[
\Rightarrow {W_2} = \dfrac{1}{2}k{\left( {2X - x} \right)^2} \\
   \Rightarrow {W_2} = \dfrac{1}{2}k{\left( {2x} \right)^2} - \left( {\dfrac{1}{2}k{x^2}} \right) \\
   \Rightarrow {W_2} = 2k{x^2} - \left( {\dfrac{1}{2}k{x^2}} \right) \\
  \therefore {W_2} = \dfrac{3}{2}k{x^2} \\
 \]
Now divide ${W_1}$ by ${W_2}$
\[
  \dfrac{{{W_2}}}{{{W_1}}} = \left( {\tfrac{{\dfrac{3}{2}k{x^2}}}{{\dfrac{1}{2}k{x^2}}}} \right) \\
   \Rightarrow \dfrac{{{W_2}}}{{{W_1}}} = 3 \\
 \]
This is the required answer

Note: The work we apply to stretch the spring is the work consumed in overcoming the stiffness of the spring, now as the spring is stretched it will again due to its stiffness we try to regain its original position now as we applied the force to hold the spring in stretched position its stiffness is getting stored as the potential energy in it as soon as we release the applied force the potential energy will be converted into kinetic energy and spring we go back into its initial position. The Law of conservation of energy is also satisfied here.