Question

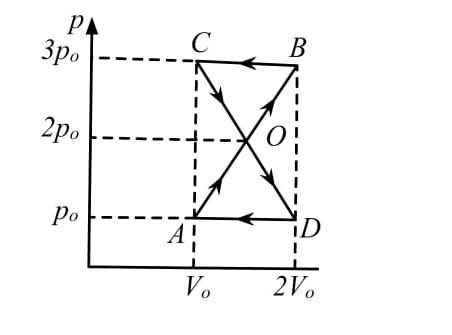
A thermodynamic system undergoes cyclic process ABCDA as shown in the figure. The work done by the system is:

A) ${P_0}{V_0}$
B) $2{P_0}{V_0}$
C) $\dfrac{{{P_0}{V_0}}}{2}$
D) $Zero$

Answer 1

Hint: In order to solve this question, the work done can be calculated by computing the area covered by the pressure-volume graph. The reason is that the work done in a gas is the product of pressure and the volume.
Work done, $W = PV$
Hence, we consider the area under the curve of a P-V graph.

Complete step by step solution:
The work done is defined as the product of the force and the displacement.
$W = Fs$
The pressure is defined as the force per unit area.
$P = \dfrac{F}{A}$

If we consider a gas at a pressure P in a container of cross-section area A, the force exerted is given by –
$F = PA$
Substituting the force in the work done, we get –
$W = PAs$
The product of the area of cross-section of the container of the gas and the distance it travels horizontally, is equal to the volume swept by the gas.
Volume, $V = As$
Hence, the work done is given by –
$W = PV$
Since the work done is the product of pressure and volume, if we plot a graph of pressure and volume of the gas, the area under the curve will be equal to the work done.
If the graph is clockwise, the work is done on the system and its value is positive. If the graph is anti-clockwise, the work done by the system and the value is negative.
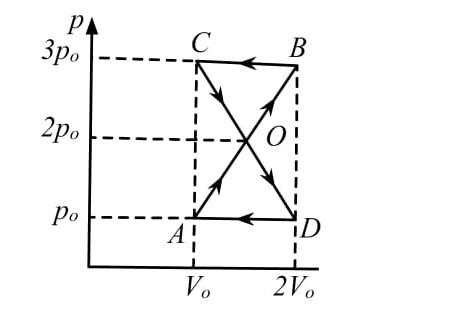
Consider a P-V graph as shown:

Work done in the entire process = Area of figure ADOBC
Area of figure ADOBC = Area of triangle AOD + Area of triangle BOC
To calculate the area of triangle AOD, ${A_1}$:
${A_1} = \dfrac{1}{2} \times b \times h$
where b = base of triangle and h = height.
Base, $b = 2{V_0} - {V_0} = {V_0}$
Height, $h = 2{p_0} - {p_0} = {p_0}$
Hence, area of AOD –
$\Rightarrow {A_1} = \dfrac{1}{2} \times {P_0} \times {V_0} = \dfrac{{{P_0}{V_0}}}{2}$
Since the triangle AOD is clockwise, the work done is positive.
$\therefore {W_1} = {A_1} = \dfrac{{{P_0}{V_0}}}{2}$
To calculate the area of triangle BOC,${A_2}$:
$\Rightarrow {A_2} = \dfrac{1}{2} \times b \times h$
where b = base of triangle and h = height.
Base, $b = 2{V_0} - {V_0} = {V_0}$
Height, $h = 3{p_0} - 2{p_0} = {p_0}$
Hence, area of BOC –
$\Rightarrow {A_2} = \dfrac{1}{2} \times {P_0} \times {V_0} = \dfrac{{{P_0}{V_0}}}{2}$
Since the triangle BOC is anti-clockwise, the work done is negative.
$\therefore {W_2} = {A_2} = - \dfrac{{{P_0}{V_0}}}{2}$
Total work done = ${W_1} + {W_2} = \dfrac{{{P_0}{V_0}}}{2} + \left( { - \dfrac{{{P_0}{V_0}}}{2}} \right) = 0$
Therefore, the work done is equal to 0.

Hence, the correct option is Option D.

Note: When two quantities in general, are plotted on a graph such as A v/s B, the following rules are applicable:
1. The product AB is represented by the area under the curve.
2. The ratio $\dfrac{A}{B}$ represents the slope of the tangent at each point on the curve.