
A uniform magnetic field B exists in the region between
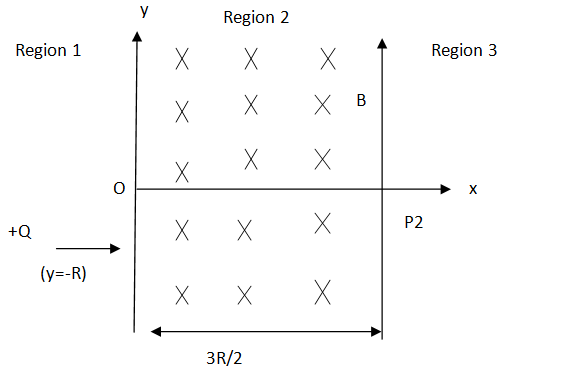
A) For
B) For
C) For a fixed B, particles of same charge
D) When the particle re-enters region 1 through the longest possible path in region 2, the magnitude of the change in its linear momentum between point P1 and the farthest point from y- axis is
Answer
147k+ views
Hint: The above question will counter the Centripetal force and electromagnetic force.
Centripetal force comes into play when the path taken by charge is circular and the electromagnetic force is seen when a charge moves in a magnetic field and the charge experiences the force.
Centripetal force is given by;
Electromagnetic force is given as:
On equalizing the two forces we will solve the given problem.
Complete step by step solution:
Let us define centripetal force and Electromagnetic force in more detail first before doing the calculation.
A centripetal force is a net force that acts on an object to keep it moving along a circular path. As per Newton's first law of motion, an object keeps on moving along the same straight path unless an external force is applied on it, by external force we mean here the centripetal force. Centripetal force is not the fundamental force but a force that keeps the object intact while moving in a circular path.
Electromagnetic force: Electromagnetic force is a type of physical interaction that occurs between electrically charged particles. It acts between charged particles and is the combination of all magnetic and electrical forces. The electromagnetic force can be attractive or repulsive.
Now, we will come to the calculation part of the problem.
For the charge Q to return to region 1, the radius of the circular path taken by charge must be
Therefore, we will equate centripetal force and electromagnetic force.
We will cancel the common terms from the above written equation and substitute
From equation 2 we can conclude that B should be greater than or equal to
Option A is correct.
When
Again on equating centripetal force and electromagnetic force and substituting the value of B from equation 3
On cancelling the common terms we have;
Thus, particles enter region 3 through point P2 on the x-axis as
Option B is correct.
Thus, option C and D are incorrect.
Option A and B are correct.
Note: Electromagnetic force has many applications such as motion of the conductor in magnetic field when current is allowed to pass through the conductor (in alternators, dc motors). Similarly Centripetal force too has applications like the rotation and revolution of planets around the sun is possible all because of centripetal force.
Centripetal force comes into play when the path taken by charge is circular and the electromagnetic force is seen when a charge moves in a magnetic field and the charge experiences the force.
Centripetal force is given by;
Electromagnetic force is given as:
On equalizing the two forces we will solve the given problem.
Complete step by step solution:
Let us define centripetal force and Electromagnetic force in more detail first before doing the calculation.
A centripetal force is a net force that acts on an object to keep it moving along a circular path. As per Newton's first law of motion, an object keeps on moving along the same straight path unless an external force is applied on it, by external force we mean here the centripetal force. Centripetal force is not the fundamental force but a force that keeps the object intact while moving in a circular path.
Electromagnetic force: Electromagnetic force is a type of physical interaction that occurs between electrically charged particles. It acts between charged particles and is the combination of all magnetic and electrical forces. The electromagnetic force can be attractive or repulsive.
Now, we will come to the calculation part of the problem.
For the charge Q to return to region 1, the radius of the circular path taken by charge must be
Therefore, we will equate centripetal force and electromagnetic force.
We will cancel the common terms from the above written equation and substitute
From equation 2 we can conclude that B should be greater than or equal to
Option A is correct.
When
Again on equating centripetal force and electromagnetic force and substituting the value of B from equation 3
On cancelling the common terms we have;
Thus, particles enter region 3 through point P2 on the x-axis as
Option B is correct.
Thus, option C and D are incorrect.
Option A and B are correct.
Note: Electromagnetic force has many applications such as motion of the conductor in magnetic field when current is allowed to pass through the conductor (in alternators, dc motors). Similarly Centripetal force too has applications like the rotation and revolution of planets around the sun is possible all because of centripetal force.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
EMI starts from ₹2,775 per month
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Ideal and Non-Ideal Solutions Raoult's Law - JEE




