Question

A uniform magnetic field of induction B fills a cylindrical volume of radius R. A rod AB of length 2l is placed as shown in fig. If B is changing at the rate $dB/dt$, the emf that is produced by the changing, magnetic field and that acts between the ends of the rod is:

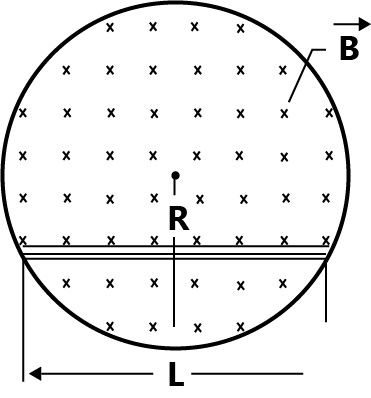
(A) $\dfrac{{dB}}{{dt}}l\sqrt {{R^2} - {l^2}} $
(B) $\dfrac{{dB}}{{dt}}l\sqrt {{R^2} + {l^2}} $
(C) $\dfrac{1}{2}\dfrac{{dB}}{{dt}}l\sqrt {{R^2} - {l^2}} $
(D) $\dfrac{1}{2}\dfrac{{dB}}{{dt}}l\sqrt {{R^2} + {l^2}} $

Answer 1

Hint: First of all, we will calculate the area of triangle AOB. We will use the concept of rate of change of magnetic flux as emf or induced voltage in the cylinder. We will use $emf = A\dfrac{{dB}}{{dt}}$ formula to calculate the emf produced at both the ends of the rod.

Complete step by step answer:

Magnetic field of induction B:
It is defined as the number of magnetic field lines passing a unit surface area normally.
Emf: Rate of change of magnetic flux is known as emf. It is deNoted by $\varphi $. It is also known as voltage.
Mathematically, emf is an integral multiple of magnetic flux crossing area element dA.
${\varphi _B} = \iint\limits_A {B.dA}$
Differentiating on both the sides, we get
$emf = \dfrac{{d\varphi }}{{dt}}$$ = A\dfrac{{dB}}{{dt}}$
Magnetic field is confined in a cylinder of radius R.
Length of rod = AB = 2l
Rate of change of magnetic field $ = \dfrac{{dB}}{{dt}}$
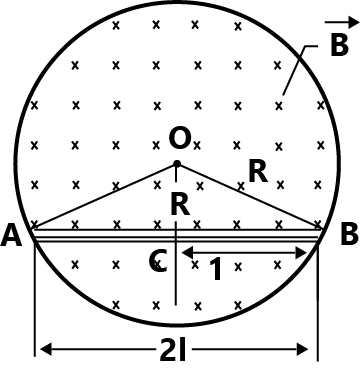
According to figure;
Area of triangle AOB = A
Using Pythagorean Theorem,
$OC = \sqrt {O{B^2} - C{B^2}} $
OB = radius of circle = R
CB = half of length of rod AB = l
$OC = \sqrt {{R^2} - {l^2}} $
Area of a triangle $ = \dfrac{1}{2} \times base \times height$
$ = \dfrac{1}{2} \times OC \times AB$
$ = \dfrac{1}{2}2l\sqrt {{R^2} - {l^2}} $
$ = l\sqrt {{R^2} - {l^2}} $
Emf induced at the midpoint of rod AB is
$\varepsilon = \dfrac{{dB}}{{dt}}l\sqrt {{R^2} - {l^2}} $

Therefore, option A is correct.

Note:
If Pythagorean theorems have been used then $\sqrt {{R^2} + {l^2}} $ will not come in the solution. Option B and D will be wrong. If the length of rod is taken as l instead of $\dfrac{l}{2}$ then flux calculated will not be at mid-point. That’s why option A is the correct solution.