Question

A uniform rod of 20 kg is hanging in a horizontal position with the help of two threads. It also supports a 40 kg mass as shown in the figure. Find the tensions developed in each thread.

Answer 1

Hint: We will draw a free body diagram. We will calculate tension in string using translational equilibrium using $\mathrm{\Sigma }F=0$. Then using rotational equilibrium $\tau =0$, we will calculate individual tensions at point C and D.

Complete step by step answer:

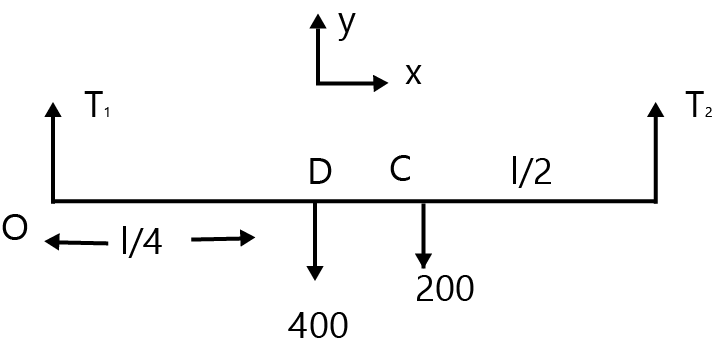
Free body diagram is shown in the figure.
Translational Equilibrium:
A body moving with constant velocity or no acceleration. Then it is said to possess translational equilibrium.
$\mathrm{\Sigma }F=0$
$\Rightarrow \mathrm{\Sigma }ma=0$
$\Rightarrow a=0$
$\Rightarrow {\displaystyle \frac{dv}{dt}}=0$
$v=const$
Rotational Equilibrium:
A body experiencing a constant rotational velocity or no angular acceleration.
$\mathrm{\Sigma }\tau =0$
$\mathrm{\Sigma }r\times F=0$
$F=0$
In this case object shows a rotational motion in only one direction at a constant angular velocity
$\omega =0$
According to translational equilibrium
$\mathrm{\Sigma }{F}_y=0$
$\Rightarrow T_1+T_2=0$
$T_1$= tension in string where 40 kg mass is hanged at a distance of ${\displaystyle \frac{l}{4}}$
$T_2$= tension in string lying at a distance of ${\displaystyle \frac{l}{2}}$ at point C as shown in figure.
$=40\times 10+20\times 10$
$=400+200N$
$=600N$
According to rotational equilibrium
Applying at A, we get
${\tau }_A=0$
$\Rightarrow -400(l/4)-200(l/2)+T_{2}l=0$
$T_2=200N$
$T_1=100N$

Therefore, tension in string AB is 600 N and tensions at point D and C is 200 N and 100 N respectively.

Note:
If value of g is taken as $9.8{\displaystyle \frac{m}{{\sec }^2}}$instead of $10{\displaystyle \frac{m}{{\sec }^2}}$ then values would have been different. If the object would have been accelerating then there would be no equilibrium.
Since the direction in which force is acting at point C and D is opposite to point A and B do opposite signs will be used while doing calculation. Negative signs used while calculating torque indicates direction.